電容器耦合約瑟夫森結連接的Chua電路的同步控制

蔣玲鳳, 安新磊, 任雁瀾

(蘭州交通大學數理學院, 蘭州 730070)

在復雜的非線性系統中通過設置適當的參數通常可以觀察到混沌現象,在過去的幾十年里,混沌行為的相關問題一直受到廣泛的研究。例如,許多混沌系統被設計以產生特定的吸引子[1-3],利用混沌電路設計信號振蕩器[4]、實現安全通信和圖像加密[5-8]。此外,還提出了很多混沌控制和實現同步的方法[9-11]。結果表明,自適應控制法要比其他控制方法更具優勢,因為合適的控制器可以消耗更低的能量和更短的瞬態周期來達到目標軌道。

混沌電路之間的同步實現可以提高信號的輸出功率和強度。基于電阻的電壓耦合是常見的耦合方式,但在實現同步的過程中耦合電阻會消耗焦耳熱。近幾年,Ma等[12]、Xu等[13]基于生物學和物理學觀點提出了場耦合的概念,通過非線性器件耦合混沌電路和神經元電路,發現在不同非線性器件耦合作用下,耦合系統可以表現出豐富的動力學特征[14-18]。例如,Liu等[16]通過電容器橋接Chua電路,結果發現這種場耦合可以在不消耗焦耳熱的情況下調節無量綱混沌電路之間的同步穩定性。Yao等[17]使用可調電感線圈連接兩個Chua電路,研究發現,電感耦合有利于實現兩個混沌系統的同步。張秀芳等[18]利用光電管耦合FHN (fitz hugh-nagumo)神經元并分析其動力學特性,結果表明在耦合強度較小時, 耦合系統由于受迫共振表現為完全同步,耦合強度較大時, 耦合系統傾向于相位同步。

可調電容在調節動態特性和輸出方面起著重要的作用,其機理是耦合電容器的連續充放電改變了電容器中的電場,能量流交換得到增強,這樣就可以有效地改變耦合電路的輸出,使兩個混沌電路實現同步。通過電感線圈連接神經元可以激發磁場耦合,有效地描述化學突觸耦合[19]。事實上,電容器和電感線圈這些耦合電子元件都可以有效地橋接非線性電路來實現可能的同步,所以場耦合可以增強非線性電路之間的能量傳播,因此電場和磁場耦合均可以為神經元之間的信息傳遞提供一種可能的有效方式[20]。

約瑟夫森結是利用超導材料制作的一種具有高度非線性性的新型器件,它不僅具有高工作頻率、低噪聲和低功耗等優點,而且約瑟夫森結及其相關電路中存在著復雜的混沌動力學行為[21],因此約瑟夫森結是構建混沌電路的理想元件。Shukrinov等[22]發現,輻射會在單結中產生混沌效應,但結間耦合的效應是不同的,它可以通過與單結不同的路徑產生混沌現象。Zhang等[23]利用約瑟夫森結與電阻并聯形成混合突觸來耦合FHN神經元電路,可以通過在結之間產生加性相位誤差來估計外部磁場的影響,結果表明通過調控參數可以穩定兩個FHN神經回路之間的同步。

現以Chua電路為研究對象,并引入約瑟夫森結,通過數值模擬給出分岔圖、相圖,分析該電路的放電行為。運用電容器耦合該系統,引入外界磁場,基于同步誤差原理討論不同參數、不同外界磁場下兩個系統的完全同步行為。

1 模型描述

Chua電路經常被用于研究混沌同步和控制,是一種常見的混沌電路。該電路由兩個電容器(C1,C2)、兩個電阻器(R1,R2)、一個電感線圈L和一個非線性電阻RN組成,是一個三階自治系統,其電路的狀態變化主要依賴于電容、電感和電阻值,且對其變化的影響及其敏感。在Chua電路的基礎上引入約瑟夫森結,得到電路如圖1(a)所示,圖1(b)為非線性電阻RN的電流電壓曲線圖。

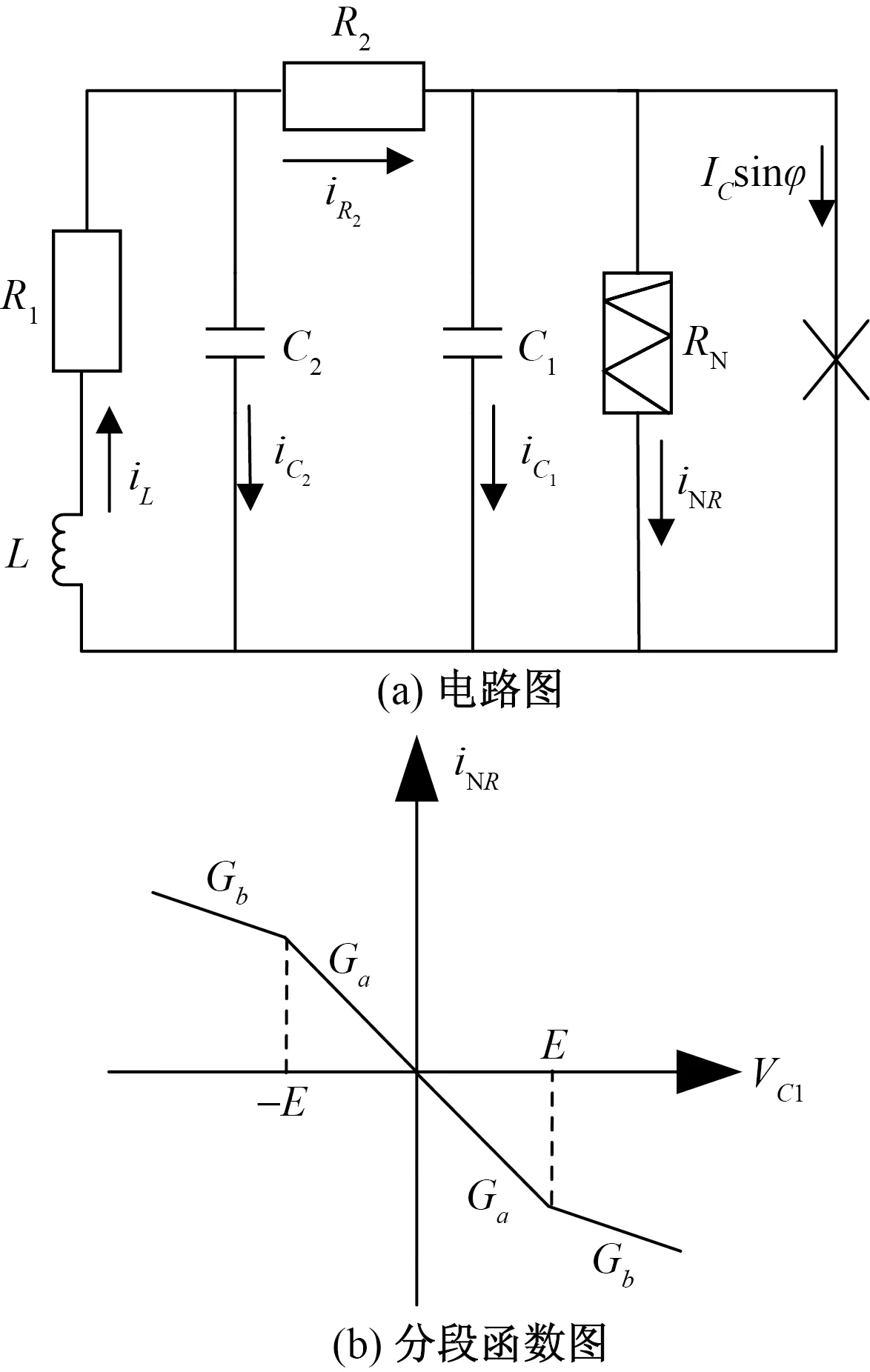
圖1 Chua電路并聯約瑟夫森結的電路圖和非線性電阻的電流電壓曲線圖Fig.1 The circuit diagram of the parallel Josephson junction of the Chua’s circuit and the current and voltage curve of the nonlinear resistor

圖1(a)中,通過約瑟夫森結的電流為

IJ=ICsinφ

(1)

式(1)中:IC為約瑟夫森結的臨界電流;φ為超導電子波函數相位差。

根據基爾霍夫定律及伏安關系可得圖1(a)的電路方程為

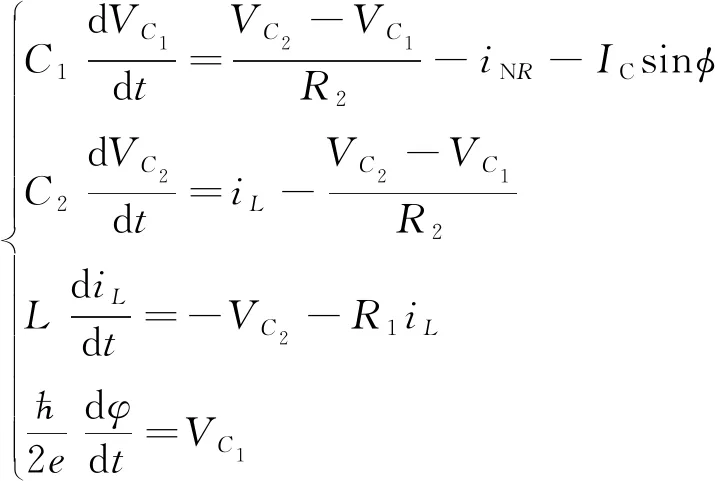
(2)

式(2)中:?為普朗克常數除以2π;VC1為約瑟夫森結兩端的電壓;e為單元電荷電量。

圖1(b)的分段函數可以描述為

iNR=GbVC1+0.5(Ga-Gb)(|VC1+E|-|VC1-E|)

(3)

為了方便數值計算和進行動力學分析,通過標準尺度變換將電路方程映射到無量綱動力系統,其標準尺度變換公式為

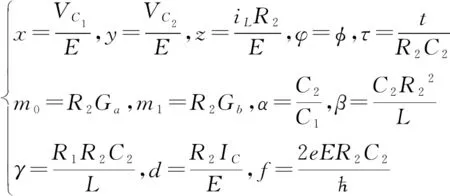
(4)

得到無量綱方程為

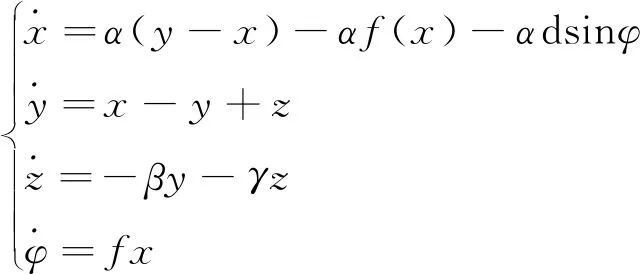
(5)

f(x)=m1x+0.5(m0-m1)(|x+1|-|x-1|)

(6)

事實上,外界恒定磁場對約瑟夫森結的通道電流和相位誤差的影響表達式為

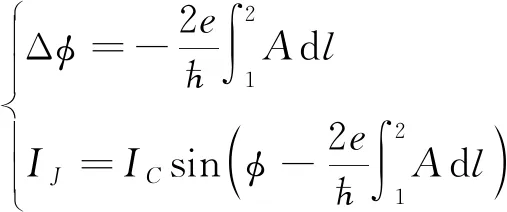
(7)

式(7)中:A表示磁矢勢;1、2表示約瑟夫森結的左右兩側,外磁場作用下的電路如圖2所示。

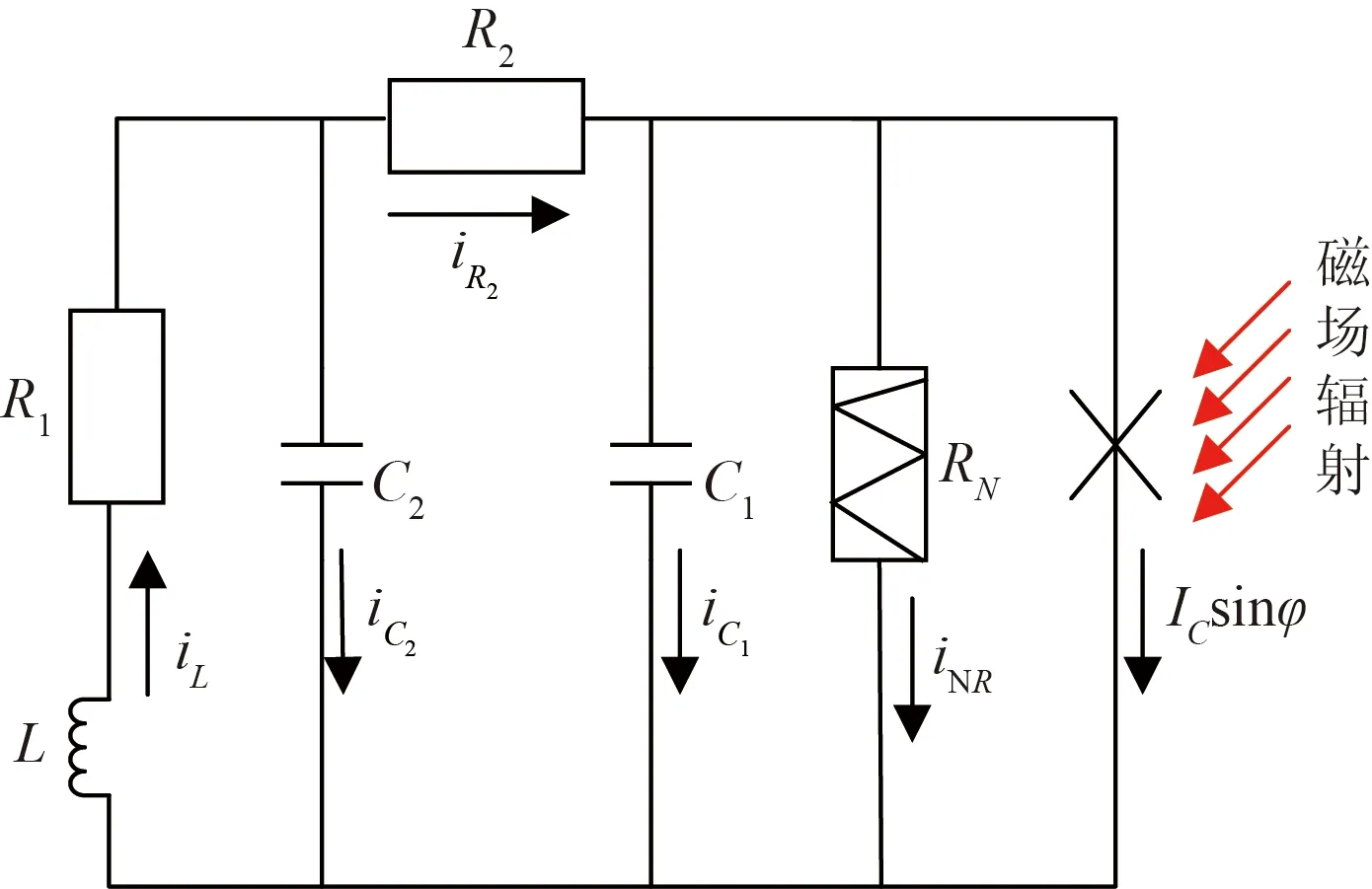
圖2 外界磁場下Chua電路并聯約瑟夫森結的電路圖Fig.2 Circuit diagram of Chua’s circuit in parallel with Josephson junction under external magnetic field

當約瑟夫森結連接的神經電路暴露在外磁場中,庫柏對的傳播將受到磁場的影響,從而使結電流受到周期性擾動[24]。考慮到磁場對約瑟夫森結的隨機干擾,其電路的動力學方程描述為

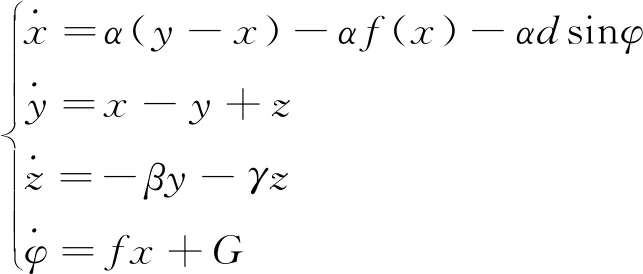
(8)

式(8)中:G表示外部磁場產生的加性相位誤差,可以通過強度和方向的變化對其調整。

混沌同步的概念是在20世紀80年代末被首次提出的,是實現混沌保密通信的關鍵技術,此外,同步是大腦記憶和存儲信息等活動的重要因素,對神經元處理以及傳遞生物信息有著重要意義。因此研究系統的同步問題是有必要的,用電容器C耦合系統(8),其電路如圖3所示。

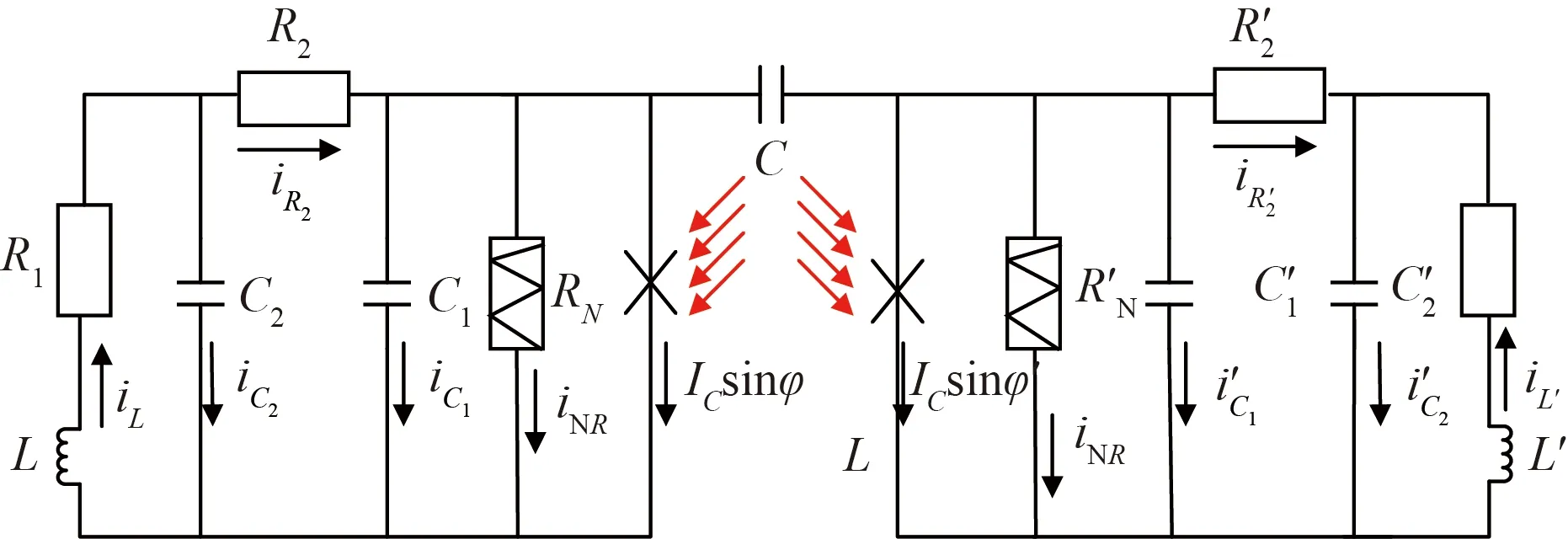
圖3 電容器耦合系統(8)的電路圖Fig.3 Circuit diagram of capacitor coupling system (8)

來自電容器的反饋電流為

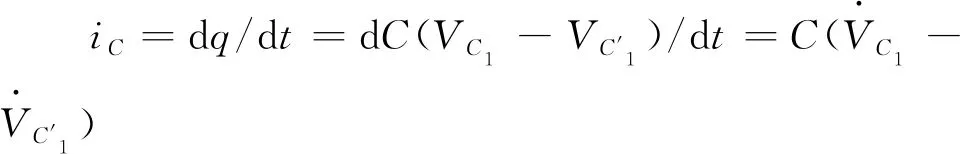
(9)

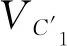
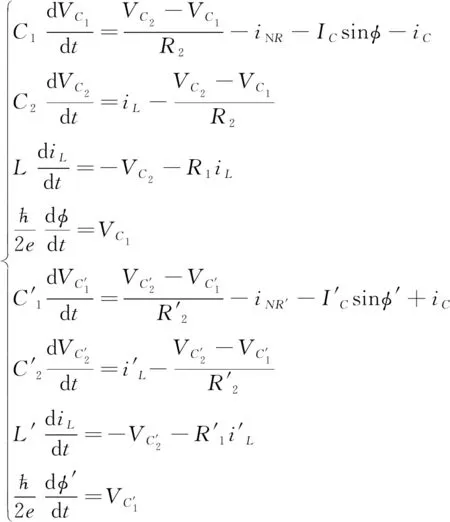
(10)

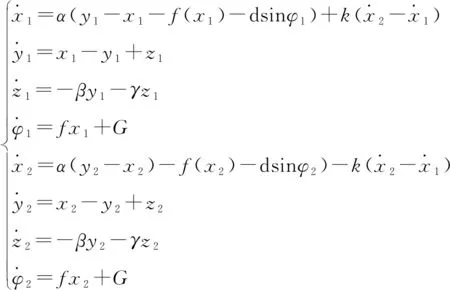
(11)

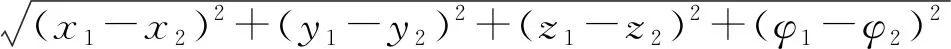
(12)

當誤差函數θ隨時間減小到零,則說明耦合系統達到了完全同步。由式(11)可知,可以控制參數k來調節軌道距離,從而使耦合系統的完全同步穩定。在實踐中,可以應用飽和增益法,即稍微增加耦合強度來尋找其臨界閾值以支持完全同步的獲得。

2 數值結果

在數值模擬中,采用四階龍格庫塔算法,積分步長h=0.01,計算的時間為t=1 000。選取兩系統的初值分別為(0.2,0.1,0.1,0.1)和(0.02,0.01,0.01,0.01),選取參數為m0=-1.296,m1=-0.738,β=19,d=2,f=0.07。考慮到系統(8)在不同的參數下會呈現不同的放電模式,因而可能會導致電路的動力學行為發生變化,首先繪制了系統(8)隨參數α變化的分岔圖,如圖4所示。

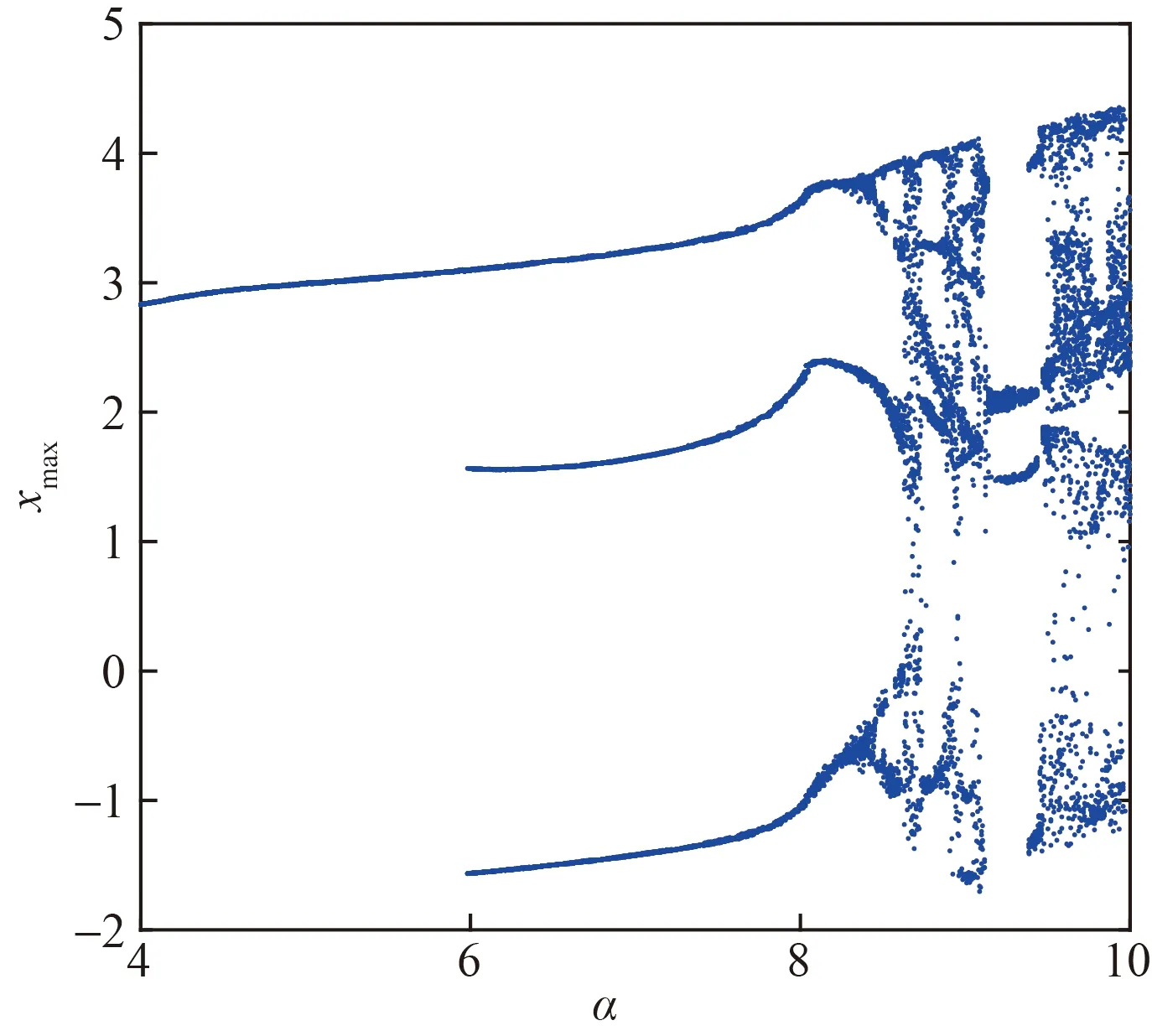
圖4 系統(8)在G=0時關于參數α∈[4,10]的分岔圖Fig.4 Bifurcation diagram of system (8) with respect to parameterα∈[4,10] when G=0

由圖4可知,隨著參數α的增加,系統(8)從周期放電通向混沌放電,當α∈[4,8.4]時,系統為周期態,當α∈[8.4,10]時,系統為混沌態。為了更清晰的觀察系統隨參數α的變化而呈現的不同放電狀態,分別取α=6和α=10,得到系統的時間序列圖及相圖如圖5所示。

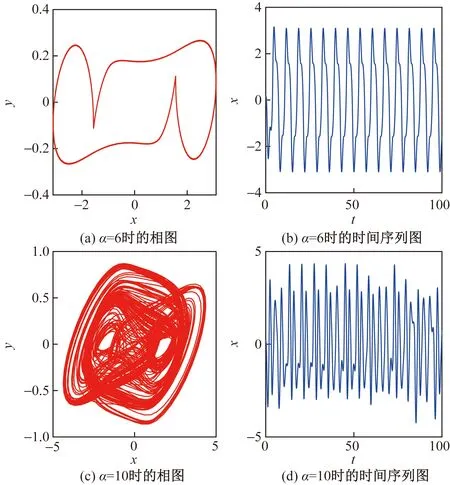
圖5 系統(8)的時間序列圖及相圖Fig.5 Time series diagrams and phase diagrams of system (8)

圖5的結果表明吸引子的形成取決于參數的設置。當α=6時,系統處于周期1簇放電,當α=10時,系統處于混沌放電,此時系統表現出雙渦卷振蕩。該結果與圖4結果一致,進一步驗證了圖4的正確性。對于耦合系統(11),主要探究耦合系統完全同步的實現與系統放電狀態的關系,分別對電容器耦合兩個周期系統、兩個混沌系統以及一個周期一個混沌系統進行討論。

首先考慮兩個參數相同的周期系統(α=6),為了探究耦合強度k和外界磁場G對系統的影響,繪制了在外界磁場G=0和G=0.7時耦合系統關于耦合強度k的最大誤差分岔圖,如圖6所示。

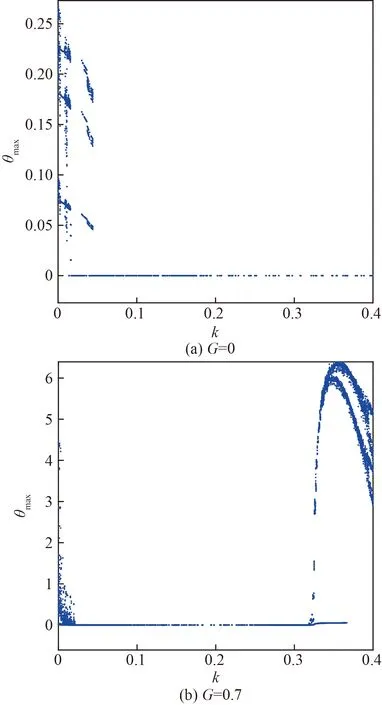
圖6 外界磁場下系統(11)的最大誤差分岔圖Fig.6 Maximum error bifurcation diagrams of system (11) under external magnetic field

圖6結果表明,外界磁場能夠改變耦合系統的放電模式。從圖6(a)可以看出,當耦合強度增加到0.045時系統的最大誤差趨于零,系統出現了不同步到完全同步的現象;從圖6(b)可以看出,當耦合強度增加到0.03時系統的最大誤差也趨于零,系統也出現了不同步到同步的現象,進一步增加耦合強度到0.31時,系統出現了去同步現象。因此,無論是否有外界磁場的作用,都能使系統達到完全同步。耦合系統在外界磁場G=0.7時的誤差演化圖如圖7所示。

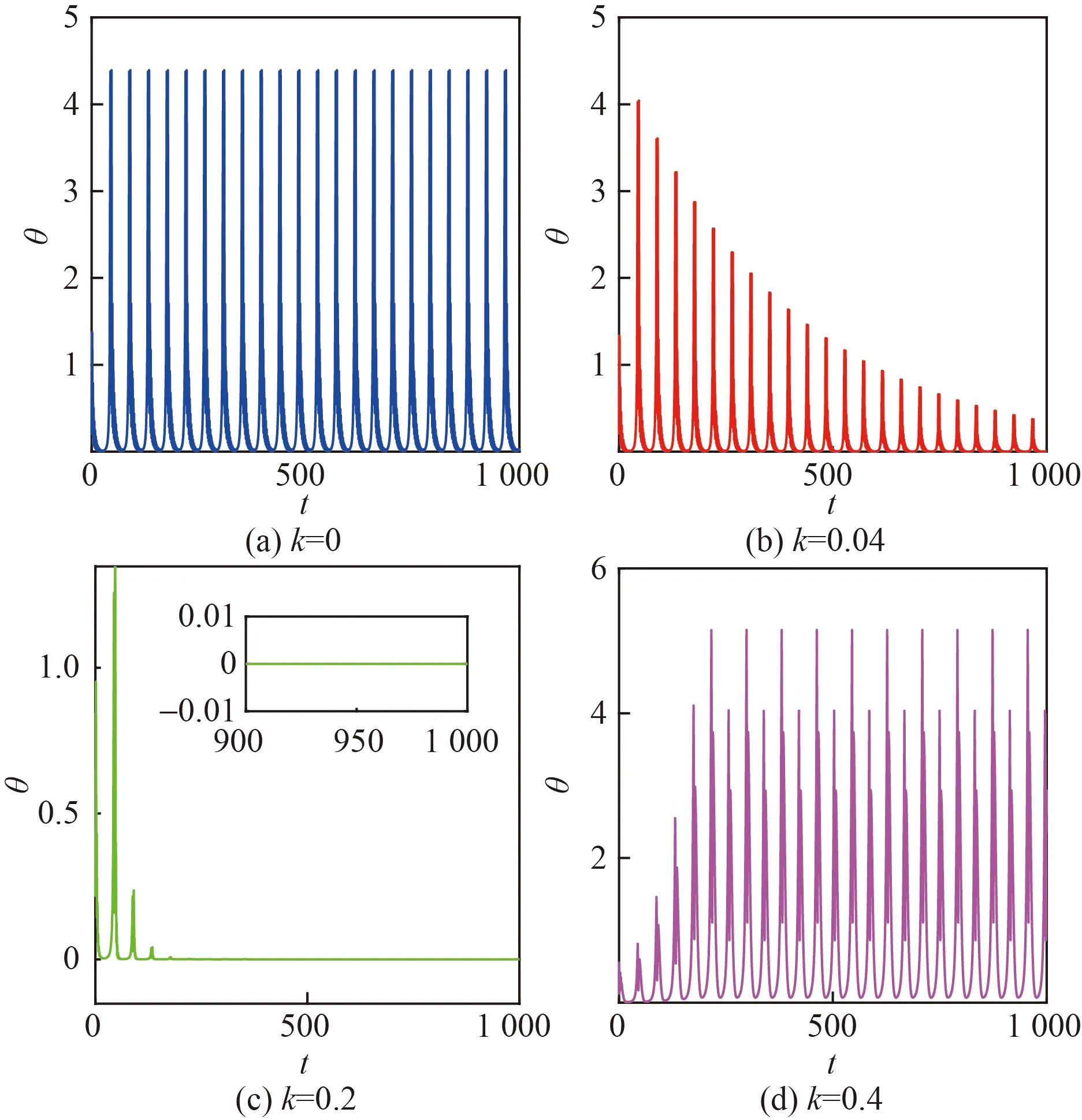
圖7 電容耦合下兩個周期系統的誤差演化圖Fig.7 Error evolution diagrams of two periodic systems with capacitor coupling

從圖7(a)和圖7(b)可以看出,隨著k的增加,同步誤差減小,系統靠近完全同步;當k=0.2時,由圖7(c)可以看出系統的同步誤差隨時間逐步減小,最終穩定于零,因此在k=0.2時耦合系統能夠實現完全同步;而當k=0.4時,同步誤差隨時間逐步增加,系統未能達到完全同步。圖7的結果與圖6(b)對應,隨著耦合強度的增加,系統經歷從不同步到完全同步再到去同步的過程。因此,在合適的耦合強度下,電容器耦合兩個全同周期系統可以實現完全同步。

下面考慮電容器耦合兩個參數相同的混沌系統(α=9),同樣,首先繪制了外界磁場G=0和G=0.1時耦合系統關于耦合強度k的最大誤差分岔圖,如圖8所示。

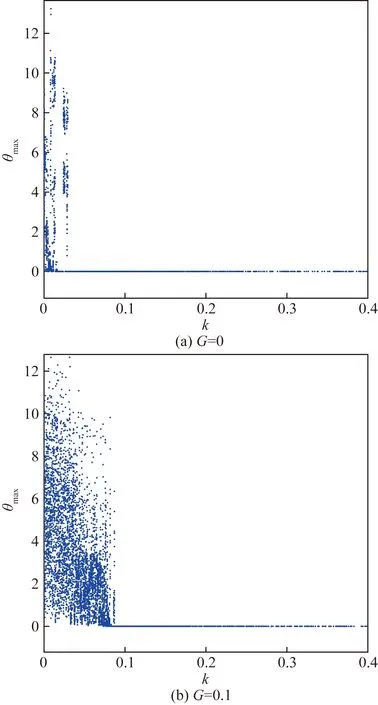
圖8 外界磁場下系統(11)的最大誤差分岔圖。Fig.8 Maximum error bifurcation diagrams of system (11) under external magnetic field

圖8表明,外界磁場可以調控系統達到完全同步時耦合強度的范圍,在該系統中,外界磁場使得系統能夠達到完全同步的耦合強度范圍減小。當外界磁場G=0時,耦合強度增加到0.03時系統的最大誤差減小到趨于零,系統出現不同步到完全同步的現象;當外界磁場G=0.1時,耦合強度增加到0.09時系統的最大誤差減小到趨于零,系統也出現了不同步到完全同步的現象。因此,無論是否有外界磁場的作用,都能使兩個不同步的混沌系統達到完全同步。圖9繪制了外界磁場G=0.1時系統的誤差演化圖。

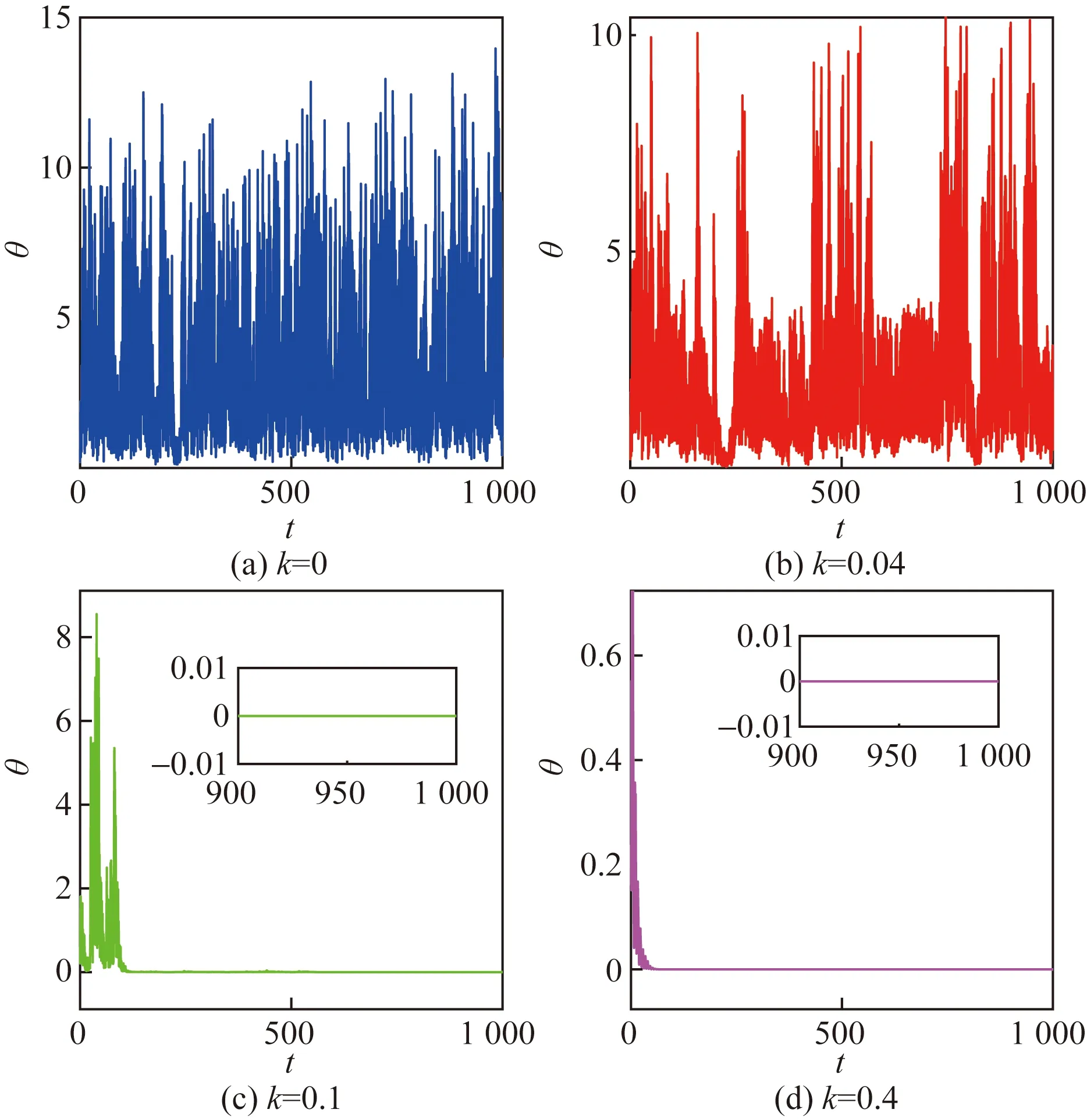
圖9 電容耦合下兩個混沌系統的誤差演化圖Fig.9 Error evolution diagrams of two chaotic systems with capacitor coupling

從圖9可以看出,隨著耦合強度的增加,同步誤差趨于減小,最終穩定于零,耦合系統實現完全同步。當k=0和k=0.04時,存在誤差,系統未達到同步;當k=0.1和k=0.4時,由放大圖可以看出同步誤差最終穩定于零,因此在k=0.2和k=0.4時耦合系統達到了完全同步,且k=0.4時效果更好。該結果與圖8(b)完全對應,因此,在合適的耦合強度下,電容器耦合兩個全同混沌系統也可以實現完全同步。

下面考慮電容器耦合一個周期系統(α=6)和一個混沌系統(α=9),即兩個參數不同的系統。首先給出了外界磁場G=0時耦合系統關于耦合強度k的最大誤差分岔圖,如圖10(a)所示。

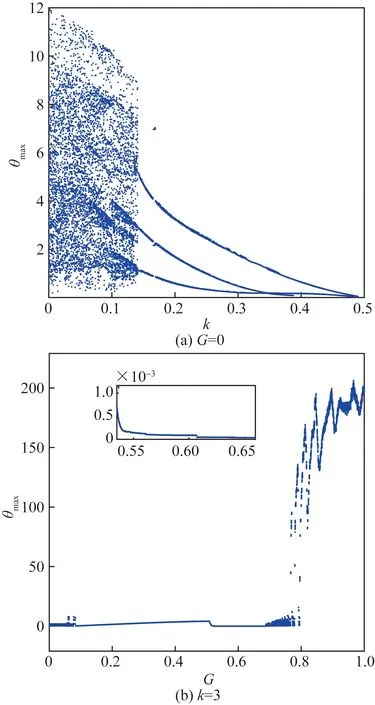
圖10 電容器耦合周期和混沌系統的最大誤差分岔圖Fig.10 Maximum error bifurcation diagrams of a capacitor coupling a period and a chaotic system

圖10(a)結果表明,無論耦合強度如何改變系統都存在誤差,因此在沒有外界磁場的作用下系統無法實現完全同步。為了找到可能使耦合系統達到完全同步的外界磁場值,固定k=0.3,繪制了關于外界磁場G的最大誤差分岔圖,如圖10(b)所示。從圖10(b)的放大圖可以看出,當G∈[0.55,0.65]時,系統的最大誤差小于10-3,因此系統在G∈[0.55,0.65]時可能達到完全同步,進一步增加磁場強度,系統的誤差也逐漸增加,因此系統在G∈[0.65,1]時無法實現完全同步。為了驗證G∈[0.55,0.65]時系統可以達到完全同步,取G=0.6,繪制了系統的誤差演化圖,如圖11所示。

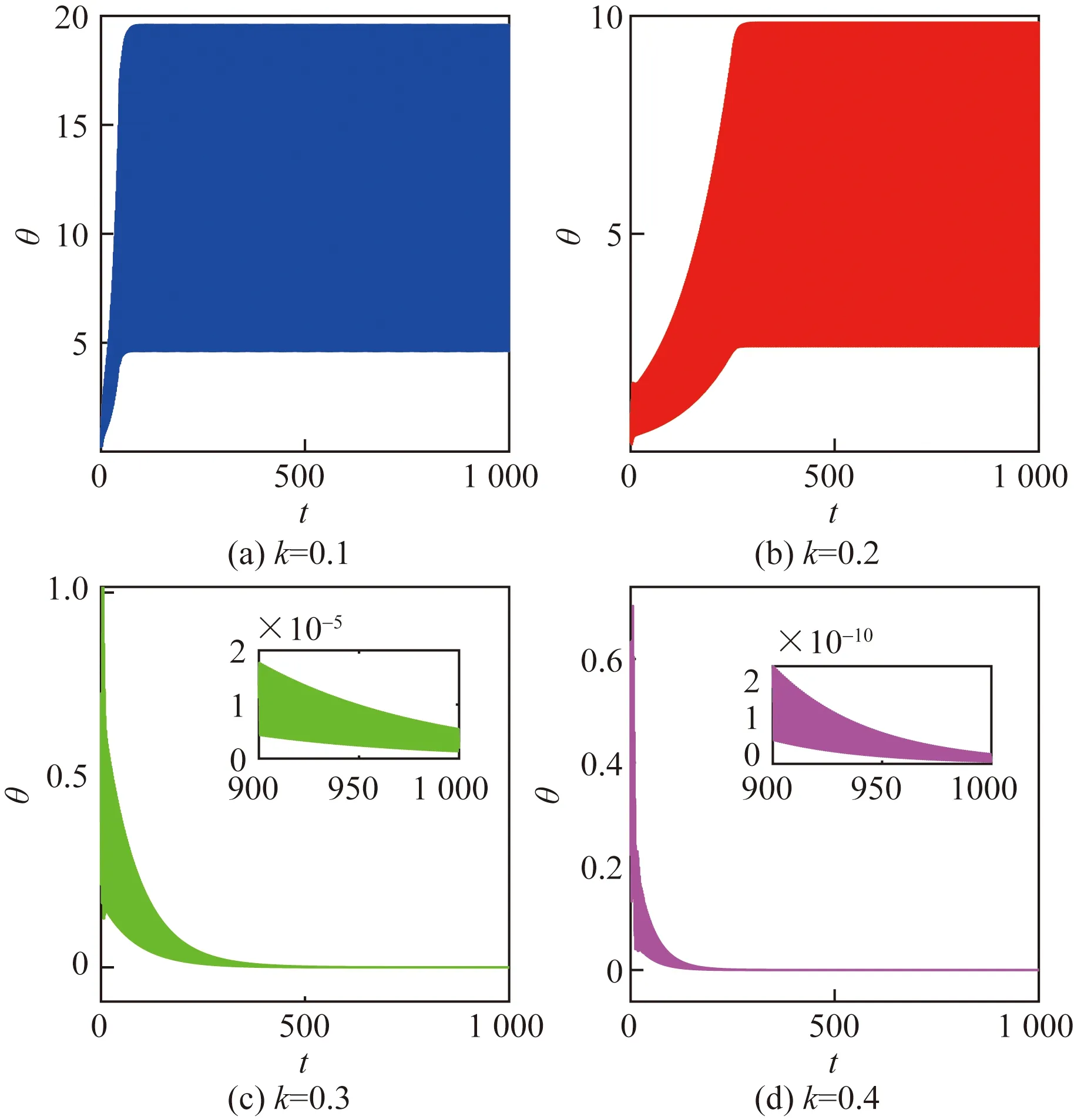
圖11 電容耦合下周期和混沌系統的誤差演化圖Fig.11 Error evolution diagrams of a periodic and a chaotic system under capacitor coupling

從圖11可以看出,當k=0.1和k=0.2時系統未達到完全同步;當k=0.3和k=0.4時,同步誤差隨時間逐步減小,由放大圖知同步誤差最終并未減小到零,但誤差非常小,因此在k=0.3和k=0.4時耦合系統幾乎達到了完全同步,將它稱為幾乎完全同步。因此,在合適的外界磁場以及一定的耦合強度下,電容器耦合周期和混沌系統可以達到幾乎完全同步。

綜上所述,在沒有外界磁場時,調控耦合強度可以使電容器耦合兩個全同周期系統和兩個全同混沌系統實現完全同步,但無法使兩個參數不同的系統達到完全同步。當存在外界磁場時,不僅可以使兩個全同周期系統和兩個全同混沌系統達到完全同步,并且在外界磁場G=0.6時,還可以使電容器耦合周期和混沌系統達到幾乎完全同步。

3 結論

首先通過對約瑟夫森結連接的Chua電路方程無量綱化得到一般的動力學方程,并結合數值模擬分析了該系統的放電行為。其次,用電容器耦合該系統,分類討論了耦合系統在不同放電模式下達到完全同步所需要的條件,結果表明,在合適的外界磁場和一定的耦合強度下,耦合系統能夠實現完全同步或者幾乎完全同步。對比Chua電路,該系統可以產生更復雜的混沌行為,而混沌時間序列可以生成安全密鑰來進行安全通信,因此可以將此系統用于通信保密。