基于NS/CFIE 伴隨方程的飛行器氣動隱身綜合優化

黃江濤，周琳，陳憲，*，馬創，劉剛，高正紅

1.中國空氣動力研究與發展中心 空天技術研究所， 綿陽 621000

2.西北工業大學 航空學院， 西安 710072

未來先進作戰飛機氣動布局的重要發展方向為扁平化、高度融合，因此對氣動隱身一體化設計技術提出了新的挑戰，而先進氣動布局設計技術是實現未來作戰飛機高隱身、高機動、寬速域、遠航程等技術指標的關鍵環節。近年來，在飛行器多目標、多學科優化上取得了豐碩的研究成果，尤其是高維設計變量、高維目標空間以及高保真度設計技術上取得了長足進展。但對于實際問題仍然存在以下瓶頸，限制了設計技術的工程實際應用：

1）氣動外形精細化優化需求帶來的學科分析精度的限制。工程分析方法一定程度上力不從心，尤其對于強非線性流動問題。例如，傳統的面元法、速度勢方程等在初步選型迭代、性能估算方面具有重要作用，但很難滿足氣動精細化階段設計問題［1-3］。而另一方面，基于高可信度氣動分析技術進行氣動優化又導致了龐大的計算資源需求。

2）高頻段的電磁散射設計導致的龐大計算量。高頻段飛行器的隱身優化設計，帶來設計變量空間維度較大，從而導致優化搜索量倍增；電磁計算網格規模龐大的問題，導致計算資源倍增，對于大尺度飛行器的氣動外形設計與評估，即便是低頻隱身設計，綜合優化帶來的高精度電磁計算量也是極為龐大的。

3）精細化/高可信度隱身設計需求導致的龐大計算量與內存資源需求。現有飛行器氣動外形隱身設計研究中多采用幾何光學法（GO）、物理光學法（PO）、幾何繞射理論（GTD）、物理繞射理論（PTD）等高頻近似算法，雖然計算速度快、所需內存小，但高頻方法的理論模型粗糙，近似過程中會忽略一些關鍵部件間的重要電磁耦合關系，在處理包含大尺寸、小尺寸結構并存的復雜外形時精度較低［4-5］。

4）高維度設計變量、高可信度優化設計需求帶來的優化算法、計算資源挑戰。傳統梯度尋優算法計算量正比于設計變量個數，進化算法所需種群規模與設計變量呈指數關系增長，導致計算量與資源需求呈指數增長；即使是采用響應面、Kriging、神經網絡等模型［6-8］進行近似處理，仍然面臨樣本需求龐大、維度障礙、預測精度差等問題，在高維度設計變量問題中仍存在一定的短板。

由于多學科伴隨體系［9-10］具有梯度計算量與各個學科設計變量個數均無關等優點，且通過耦合伴隨方程的求解能夠快速計算出各個學科關心的學科目標函數對所有設計變量的導數，倍受研究人員與工程師的關注與喜愛，同時也是國內外知名研發機構的重點發展方向［11-19］，必將在未來多學科優化領域發揮重要作用。針對作戰飛機氣動隱身一體化高可信度優化設計面臨的上述難題，結合氣動隱身多學科伴隨方程構造以及靈敏度分析的優勢，本文開展了基于NS（Navier-Stokes）/MLFMA（Multi-Level Fast Multipole Algorithm，多層快速多極子）方程及其離散伴隨方程的飛行器氣動隱身伴隨優化設計技術研究，并針對低頻雷達波環境氣動隱身一體化設計進行了初步測試。

1 流場/電磁“耦合”伴隨方程

首先，給出伴隨方程基本形式：

式中：I 表示目標函數；W 表示狀態變量；R 表示控制方程的殘差；Λ 表示伴隨變量。其中，伴隨算子Λ 既可以是單學科伴隨算子，也可以是多學科伴隨算子［9］，對應的殘差同樣也可以是多學科約束，采用相同方式進行伴隨方程推導，可以得到多學科耦合伴隨方程。采用式（1）向量求導形式可以直接推導出流場/電磁“耦合”伴隨方程：

式中：Ra、RE分別代表流場殘差與電磁數值計算殘差；wi、Aj分別代表流 場 變 量 與電流分布；I 為表面感應電流。顯然式（2）交叉導數雅克比矩陣為0，即：

“耦合”伴隨方程退化為

從式（4）可以看出，氣動電磁多學科伴隨方程完全解耦，不存在耦合，這對研發體系來講難度大大降低，2 個伴隨方程完全獨立求解。基于高可信度流場電磁伴隨優化的方面的研究從發表文獻上看幾乎是空白。一個主要原因是學科跨度較大，變分困難，計算量龐大。在流場伴隨與電磁伴隨優化基礎上，本文基于矩量法構建了氣動隱身高可信度優化系統［20］，為氣動隱身綜合優化設計奠定了技術基礎［9，21］，在此基礎之上將電磁伴隨方程推廣至多層快速多極子算法，大幅提高在工程使用中效率與可行性，提升工程設計中的應用頻段范圍。

2 基于NS 的流場伴隨方程

基于NS 的離散伴隨方程對的構造主要依賴于空間離散格式、插值精度、邊界條件處理方式的選擇，不同的空間離散格式以及插值精度會產生不同的模板需求，尤其對于高精度格式來講，其無黏項的離散伴隨構造將及其復雜。空間離散方法采用二階精度的中心格式，該格式構造簡單，在亞、跨、超聲速流場數值模擬中表現魯棒，在實際工程應用較多［22］。

將上述結果進行整合，并加入偽時間項可以得到離散伴隨主控方程：

式中：V 為電磁激勵。對式（6）的迭代求解，可以采用顯式經典四步龍格-庫塔推進，也可以采用隱式時間推進。由于式（6）在形式上與NS 方程一致， LU-SGS 方法及其最大特征值分裂方法可以用于離散伴隨求解，因此，本文采用LU-SGS時間推進方法。流場時間推進采用的隱式邊界條件在離散伴隨方程中依然可用：

3 基于MLFMA算法的混合場積分伴隨方程

在電磁散射計算中，由于混合場積分方程（Combined Field Integral Equation，CFIE）可以避免電場積分方程（Electric Field Integral Equation，EFIE）和磁場積分方程（Magnetic Field Integral Equation，MFIE）存在的“內諧振”問題，同時具有較好的條件數，且魯棒性較好，因此，在封閉外形的電磁散射計算中通常采用多層快速多極子方法求解CFIE 方程，基于電磁場表面積分方程的RCS 求解方法，電磁散射最優化問題可以表示為

結合式（1）可得隱身問題對應的伴隨方程：

相對于有限差分計算來講，基于矩量法的電磁伴隨求解將靈敏度計算效率提高2 個量級以上，且隨著入射頻率的增加，加速效果更加明顯。然而，矩量法伴隨方程面臨兩個問題：阻抗矩陣存儲空間瓶頸、幾何擾動進行阻抗矩陣裝配時間消耗。兩方面因素較大程度限制了電磁伴隨優化在大尺度特征飛行器、復雜氣動構型問題中的應用。

針對該問題本文基于多層快速多極子算法開展伴隨方程構造以及梯度計算研究。對于磁場積分方程和混合場積分方程，由于MFIE 和CFIE 阻抗矩陣與其轉置并不相等，因此無法直接建立伴隨變量與正計算結果的關系。多層快速多極子算法計算遠相互作用矩陣與相應元素電流的矢量乘ZfarI，在遠相互作用矢量乘的計算過程中不顯式存儲Zfar，無法通過改變Z 的索引方向對多層快速多極子的阻抗矩陣進行轉置運算，同時多層快速多極子算法采用廣義極小殘差法（General Minimum Residual Method，GMRES）迭代法對離散方程進行求解，因此伴隨方程求解的核心在于計算ZTI，具體計算分為近場矢量乘和遠場矢量乘兩部分。

近場矢量乘計算在最細層進行，在并行多層快速多極子算法框架下附近組元素按照塊狀分布，在存儲中僅需要保存每一塊的起始行號、起始列號、行數和這一塊中所有附近元素即可；在近場并行計算中將基函數分配到不同進程進行計算和存儲，在正計算中通常采用按行分配的方式，顯然，由于轉置原因，在伴隨計算中應采取按列分配的方式，確保同一列的元素保存在同一進程，伴隨計算的近場矩陣乘可以寫為伴隨計算的遠場矢量相乘與正計算的較為相似，但在計算順序和波的傳播方向上與正計算有所區別。伴隨計算遠相互作用矢量乘的需要在相乘的過程中交換場、源點的位置，伴隨計算遠相互作用的矢量乘可以表示為

注意到在進行伴隨矩陣乘時，首先計算電流Ii與配置因子的乘積；轉移時轉移因子為αm′m與正計算的αmm′方向相反。式（11）中Ii為第i 個源 點 的 電 流 幅 度，Vfmj、αmm′和Vsm′i分 別 表 示 配置、轉移和聚合因子，*表示共軛運算，伴隨方程中配置、轉移和聚合因子表達式與正計算問題基本一致，歸納伴隨計算與正向計算的幾個細節差異：

3）多極配置過程，伴隨計算中多極配置中使用e-ik(l-1)n′rmlml-1將聚合量從父組中心轉移到子組中心，在正計算中使用eik(l-1)n′rmlml-1進行轉移計算。

綠色高等植物都是由很多細胞組成的，植物受凍實際上就是某個部位的細胞受凍。一般地，處于休眠狀態的植物細胞早就做好了耐凍的準備，從夏天就開始逐漸脫水，冬天芽細胞斷開與維管束之間的聯接，處于最低含水量狀態，不做任何新陳代謝活動，細胞原生質內存儲的蛋白質、糖和淀粉等高分子物質使細胞質溶液保持一個最低的結冰溫度數值 （也就是冰點溫度），這樣就保證細胞質在0℃以下的環境中也不會結冰。當氣溫下降到細胞難以抵擋的時候，植物還有最后一招，那就是首先在細胞之間結冰，這樣，如果低溫很快就過去，那么細胞間的冰晶就會逐漸融化而不會傷及細胞內，使果樹遭受最小的傷害。

上述計算過程的表達式及其具體含義是計算電磁學中的常見要素，具體可參考文獻［23-24］，這里不再贅述。

至此，伴隨方程左端項推導已經完成，進一步我們需要解決右端項變分。伴隨方程（10）的右端項激勵?σ ?I 為雷達散射截面關于感應電流的導數，現就?σ ?I 的計算方法進行推導。求解得到表面感應電流分布后可以通過式（13）求得RCS：

式中：上劃線-表示共軛。由鏈式求導法則：

復數求導需分別對其實部和虛部求導，即：

則式（16）可以整理為

式（15）中g 離散后可以寫成感應電流和的形式，以RWG 基函數為例寫出g 的具體表達式：

式中：In為第n 條邊上基函數的權重，推導得到?g ?In和?gˉ?In的表達式：

從上述過程容易看出，電場積分伴隨方程是自我伴隨方程，而混合場積分伴隨方程的自我伴隨特性消失。通過伴隨方程求解得到Λ 后，根據式（21）可將伴隨梯度表示為

需要指出的是，在依據式（21）進行梯度計算的過程中，由于擾動外形的底層盒子分布與初始外形可能存在差異，導致基函數的局部編號也會有所不同，因此在存儲正計算電流和伴隨計算電流的時候需根據基函數的全局編號或面元的全局編號進行存儲。

4 飛行器氣動/隱身綜合優化設計體系

基于上述伴隨體系的構建，結合參數化建模模塊、SQP 尋優算法以及網格變形技術［25］，本文建立了基于跨學科伴隨體系的飛行器氣動隱身綜合優化平臺AR3Design。圖1 給出了建立的飛行器氣動隱身綜合優化平臺的工作流程圖。在優化過程中，參數化建模運算建立表面網格和設計變量之間的映射，通過尋優過程，得到新的設計變量，進而得到新幾何外形的表面網格。網格變形技術基于新的表面網格，采用徑向基函數（Radial Basis Function，RBF）-無限插值（Transfinite Interpolation，TFI）網格變形技術［25］得到新外形的空間網格，之后再進行新一輪計算，直至優化過程收斂。

圖1 飛行器氣動隱身綜合優化流程圖Fig.1 Flowchart of integrated aircraft aerodynamic stealth optimization

5 飛翼布局氣動隱身綜合設計

本文采用的類X47B 外形作為研究對象，其幾何特征如圖2 所示，基礎布局翼根采用反彎翼型、外翼段超臨界翼型生成。布局的參考面積為42.43 m2，重心位置為(xg，yg，zg)=(6.77，0，0) m，平均氣動弦長3.32 m。設計狀態：Ma=0.76， H=13 km，CL=0.36， Re=1.396×107。

圖2 幾何特征與電磁入射坐標定義Fig.2 Geometric features and definition of electromagnetic incident coordinates

隱身評估考慮f=200，500 MHz 這2 個頻點，采用垂直極化（VV），考慮方位角φ=0°～60°、θ=-10°～10°的RCS 均值，圖2 給出了方位角定義示意圖；該型飛翼布局參數化采用基于NURBS基 函 數 的FFD 進 行 參 數 化 建 模［26-27］，如 圖3所示。

圖3 飛翼布局FFD 參數化Fig.3 FFD parameterization of flying wing configuration

幾何約束考慮展向均勻分布的20 個剖面，要求各剖面外形的最大厚度不減小、容積不低于初始外形的95%。CFD 計算采用多塊對接結構網格，采用k-ω 剪切應力輸運（Shear Stress Transport， SST）湍流模型；隱身計算采用非結構表面網格，網格平均邊長Δx=0.1λ，在幾何變化劇烈的地方進行加密。開展在f=200，500 MHz 的氣動/隱身優化，驗證跨學科伴隨優化的有效性，分別記為Aero-RCS optimization 200M、Aero-RCS optimization 500M，采用加權的方式耦合氣動、隱身的設計目標，氣動隱身優化的數學模型為

初始外形的表面壓力分布如圖4 所示，其中阻力系數CD=138.7 counts、力矩系數Cm=0.020 4。初始外形在f=500，200 MHz 的RCS 均值分別為。

圖4 初始外形壓力云圖Fig.4 Pressure contour of initial configuration

優化過程采用160 個設計變量，分別在f=500， 200 MHz 這2 種不同雷達頻率下進行綜合優化，相應的收斂曲線分別如圖5 和圖6 所示。優化采用64 核心進行，總耗時30 h。因此，利用小型工作站即可開展基于伴隨方法的飛行器全機氣動隱身綜合優化。前人的研究結果也表明［21，28］，基于伴隨方程的氣動隱身優化方法具有高效、高精度的優點，伴隨方法計算得到的梯度與有限差分法高度一致，并且伴隨方法的效率是有限差分法的數10 倍。

圖5 氣動隱身綜合優化歷程（200 MHz）Fig.5 Aerodynamic stealth optimization process （200 MHz）

圖6 氣動隱身綜合優化歷程（500 MHz）Fig.6 Aerodynamic stealth optimization process （500 MHz）

伴隨優化前后氣動隱身特性對比如表1 所示，在本文算例中力矩沒有作為目標或約束進行處理，可以看出由于權重的設置以及隱身梯度的量級較大，使得RCS 單調下降，阻力呈現一定的振蕩。

表1 伴隨優化前后氣動隱身對比Table 1 Comparison of aerodynamic stealth before and after optimization

氣動隱身優化外形的表面壓力云圖如圖7 和圖8 所示。可以看到，不同頻段的綜合優化結果上表面激波強度明顯低于初始外形，接近無激波狀態；RCS 也實現了大幅度下降，驗證了本文建立的基于NS/CFIE 伴隨方程氣動隱身優化方法的有效性。

圖7 優化外形壓力分布云圖（200 MHz）Fig.7 Pressure contour of optimized configuration（200 MHz）

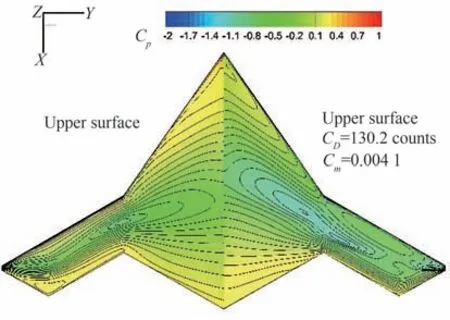
圖8 優化外形壓力分布云圖（500 MHz）Fig.8 Pressure contour of optimized configuration（500 MHz）

初始、Aero-RCS optimization 200M、Aero-RCS optimization 500M 外 形 在 翼 根（Y=0.2 m）、kink1（Y=4.5 m）、kink2（Y=8.0 m）剖面的幾何及壓力分布對比如圖9～圖11 所示。由于中央體是主要雷達散射源，在中央體附近的剖面幾何外形和壓力分布形態發生顯著變化，各個頻率優化的前緣半徑明顯減小，且呈現“鷹嘴”型；在Y=4.5 m 剖面和Y=8.0 m 剖面，前緣半徑均小于初始外形，但減小程度弱于Y=0.2 m；剖面負扭轉角度以及后加載明顯增加，2 種優化工況載荷分布更加接近橢圓，如圖12所示。

圖9 展向Y=0.2 m 優化前后對比Fig.9 Spanwise Y = 0.2 m before and after optimization

圖10 展向Y=4.5 m 優化前后對比Fig.10 Spanwise Y=4.5 m before and after optimization

圖11 展向Y=8.0 m 優化前后對比Fig.11 Spanwise Y=8.0 m before and after optimization

圖12 優化前后展向載荷分布對比Fig.12 Comparison of spanwise load distribution before and after optimization

氣動隱身優化外形優化前后，在f=200，500 MHz 的水平、垂直RCS 評估結果如圖13～圖16 所示，評估時固定φ=0°。對于垂直極化，在f=200， 500 MHz 的RCS 減縮效果非常顯著，在φ=0°～60°范圍內的RCS 均明顯降低，其中φ=55°峰值（大尺度中央體的貢獻）的高度明顯降低，φ=30°峰值高度略有降低。對于水平極化（HH），由于水平極化的RCS 主要受外形在x-y平面的幾何特征影響，剖面形狀優化雖然可以降低邊緣在水平極化的散射強度，但對水平極化入射時目標的整體RCS 特征影響不顯著，優化后外形的RCS 略有降低，但降低幅度明顯小于垂直極化。

圖13 初始與優化外形RCS 對比（f=200 MHz，VV）Fig.13 RCS comparison between initial and optimized configurations （f = 200 MHz， VV）

圖14 初始與優化外形RCS 對比（f=200 MHz，HH）Fig.14 RCS comparison between initial and optimized configurations （f = 200 MHz， HH）

圖15 初始與優化外形RCS 對比（f=500 MHz，VV）Fig.15 RCS comparison between initial and optimized configurations （f = 500 MHz， VV）

圖16 初始與優化外形RCS 對比（f=500 MHz，HH）Fig.16 RCS comparison between initial and optimized configurations （f = 500 MHz， VV）

對于目標在較低頻率的散射問題，不同散射源間的相位對總RCS 具有顯著影響。考慮相位影響時，通常采用量化RCS，其 中為 復數，定義如式（23）所示：

圖17 初始及優化外形表面散射貢獻（f=200 MHz）Fig.17 Surface scattering contribution of initial and optimized shapes （f= 200 MHz）

圖18 初始外形及優化外形表面散射貢獻（f=500 MHz）Fig.18 Surface scattering contribution of initial and optimized shapes （f= 500 MHz）

可以看到，對于f=200 MHz，面元對總RCS 的貢獻受相位影響顯著，貢獻量正負交替，間隔為半波長，全機各位置均對總RCS 有顯著影響。當f=500 MHz 時，貢獻量隨也呈現正負變化特征，但主要RCS 貢獻區域集中在布局前緣，局部特性更加顯著。對比優化前后外形，相對于初始外形，優化外形的前緣的貢獻明顯降低，其他區域的貢獻變化趨勢不明顯，甚至局部略有增加。

6 結 論

基于NS 方程以及MLFMA 算法的CFIE 方程構造了氣動隱身伴隨方程，并進一步進行氣動隱身綜合優化測試：

1）流場電磁多學科伴隨方程完全解耦，不存在耦合，2 個學科的離散伴隨方程可以完全獨立求解。

2）雷達散射伴隨計算與正向計算在多極聚合、多極轉移、多極配置以及部分場展開過程存在差異，主要體現在波方向、轉移因子等方面。

3）剖面的優化對氣動性能、垂直極化隱身效果較為明顯，剖面形狀優化雖然可以降低邊緣在水平極化的散射強度，但對水平極化入射時目標的整體RCS 特征影響較垂直極化弱。

4）飛翼布局測試算例表明，本文建立的基于NS 方程以及MLFMA 算法的氣動隱身優化方法具有極高的優化效率以及設計效果。

本文對低頻入射波條件的氣動隱身伴隨優化設計進行了研究，僅從方法角度驗證了氣動隱身伴隨方程構造的可靠性與有效性。由于AR3Design 平臺采用多層快速多極子算法、NS方程分別作為隱身、流場伴隨方程構造的基礎，因此，該伴隨優化體系具有全頻段、寬速域設計能力，基于AR3Design 開展飛行器寬頻段、寬速域、多約束氣動隱身綜合優化設計研究是本文將進一步開展的工作。