一類具有時滯的Sel’kov模型的Hopf分歧分析

馬亞妮,袁海龍,2,王雅迪

(1.陜西科技大學 數學與數據科學學院,陜西 西安 710021;2.西安交通大學 數學與統計學院,陜西 西安 710049)

0 引 言

Sel’kov模型是一個典型的反應擴散系統[1],它最初是作為糖酵解模型提出,如下所示:

式中:Ω是RN(N>1)中具有光滑邊界?Ω的有界開區域,n是?Ω上的單位外法向量,u(x,t)和v(x,t)代表時間t>0和空間位置x∈Ω時的2種反應物的濃度或2種物質的密度;參數θ是物種的擴散系數,且θ、p和λ都是正常數。該反應擴散模型(1)已被用于描述各種形式的地貌形態[2]、種群動力學[3]和自催化氧化反應[4]的研究。更多模型的背景見文獻[5-8]。

近幾十年來,模型(1)的動力學行為已經被許多生物數學家所研究。特別地,WANG通過固定p和λ(或p和θ),以θ(或λ)為分歧參數,研究了系統(1)的非常數正穩態,證明了其平衡態方程非常數正解的存在性和不存在性的條件[8]。此后,PENG討論了當θ取很大值時,若01,則會出現非常數的正穩態,表明參數p在兩反應物的空間非均勻分布中起著關鍵作用[9]。同時,PENG等也討論了在Dirichlet邊界條件下,利用不動點指數理論,給出了非負穩態解的存在性結果[10]。進一步,HAN等以參數p為分歧參數,證明在合適的條件下,該系統存在Hopf分歧解,同時建立了該周期解的穩定性和分歧方向[11],詳見文獻[12-14]。

由于種群的成長期,當前時刻的種群增長率總是與某個時刻之前的種群數量有關。這種由成長期而導致的時滯現象在種群中普遍存在。因此,近年來,在種群生態學和生物學模型中提出了具有時滯的反應擴散系統。李冬梅等研究了一類含分布時滯和Michaelis-Menten型的擴散模型,利用微分方程比較定理和Lyapunov函數方法,得到了一致持久和全局漸近穩定的充分條件[15]。王長有等利用上、下解方法及不動點理論,研究了一類反應項非單調的時滯反應擴散方程組,獲得了邊值問題周期解存在性的充分條件[16]。劉高楊等基于KADDAR和ALAOUT的模型,建立了一個帶有時滯的腫瘤免疫擴散模型,通過分析免疫細胞識別腫瘤細胞時間的閾值,可判斷腫瘤的最佳治療時間,減少患者因腫瘤導致的死亡率[17]。李振振等研究一類具有 Dirichlet邊界條件的時滯合作-擴散-平流系統,證明了時滯的增加會使正穩態解失穩,并且當時滯值穿過臨界分支點時系統會存在Hopf分歧[18]。基于以上模型的分析,將時滯引入到該系統中。本文將研究時滯對u的影響,則系統(1)可寫為

式中:τ>0代表延遲效應。

1 平衡點的穩定性與分歧的存在性

在有界開區域Ω=(0,lπ),l∈R+上考慮系統,

式中:u=u(x,t);uτ=u(x,t-τ);v=v(x,t)。定義X=C([0,lπ],R2),在抽象空間C([0,lπ],X)中,系統(4)可以寫成以下抽象的泛函微分方程

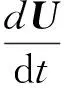
(5)

這里,dΔ=(d1Δ,d2Δ)

dom (dΔ)={(u,v)T:u,v∈C2([0,lπ],R),

ux,vx=0,x=0,lπ}

且L:C([-τ,0],X)→X,F:C([-τ,0],X)→X。

根據系統(4)有

L(φ)=[-λφ1(0)-λpφ2(0)

λφ1(-τ)+λ(p-1)φ2(0)]

F(φ)=F1(φ)F2(φ)

式中:φ=(φ1,φ2)T∈C([-τ,0],X);

F1(φ)=λ-λ[φ1(0)+1][φ2(0)+1]p+

λφ1(0)+λpφ2(0);

F2(φ)=λ[(φ1(-τ)+1)(φ2(0)+1)p]-

λ-λφ1(-τ)-λpφ2(0)。

因此系統(4)在平衡點(1,1)處的線性化可寫為

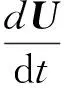
(6)

其對應的特征方程為

λy-dΔy-L[exp(λ)y]=0,

y∈dom(dΔ),y≠0

(7)

根據特征值問題

-ψ″=μψ,x∈(0,lπ),ψ′(0)=ψ″(lπ)=0

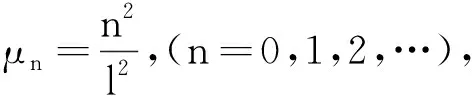
根據特征方程(7)知

λ2+Anλ+Bn+Cexp(-λτ)=0,n=0,1,2,…

(8)

C=λ2p。

若±iσ(σ>0)是式(8)的一對純虛根,則

由上述計算化簡可得

式中:

對于0≤n≤N0(p),式(10)有一個正根σn滿足

那么當

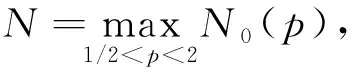
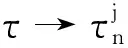
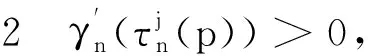
證明 將λn(τ)代入式(8)并對τ求導有

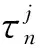
因此,根據以上引理1～3,可以得到如下結論。

2 Hopf分歧的穩定性和方向

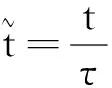
(18)

其中,對于φ∈C([-1,0],X)有

G(φ,μ)=μdΔφ(0)+μL0(φ)+

(μ+τ0)F0(φ)F0(φ)=

由第二部分可知,±iσ0τ0是線性系統的一對純虛特征值。因此有

(19)

其線性泛函微分方程為

(20)

應用Riesz表示定理可知,存在一個有界變差2×2的矩陣函數η(θ,μ)(-1≤θ≤0),使得

事實上,

η(θ,μ)=(τ0+μ)Eδ(θ)-(τ0+μ)Fδ(θ+1)

其中,

?φ(θ)∈C1([-1,0],R2),定義A(0)為

以及?ψ=(ψ1,ψ2)∈C1([-1,0],(R2)*),定義

定義雙線性函數

其中,A(0)和A*是正規伴隨算子。

易證±iσ0τ0是A(0)和A*的特征值

q(θ)=(q1,q2)Texp(iσ0τ0θ)(θ∈[-1,0])

和

分別是A(0)和A*對應于特征值iσ0τ0和-iσ0τ0的特征向量,其中

iσ0τ0exp(-iσ0τ0)

這里,u=(u1,u2),v=(v1,v2)∈X=C([0,lπ],R2)。并且對φ∈C([-1,0],X),有

線性方程(19)在μ=0時的中心子空間是PCNC,且

PCNφ=Φ(Ψ,〈φ,f0〉)0·f0,φ∈C,

對C進行空間分解,C=PCNC⊕PSC,其中,PSC表示穩定子空間。

由文獻[25]可知,線性系統(19)無窮小生成元AU滿足

由于只考慮在μ=0附近的分歧周期解的穩定性和方向,因此令系統(18)中的μ=0,可得中心流形

則系統(18)的解可以表示為

式中:

從而

記

定義

f(u,v)=λ(u+1)(v+1)p。

根據泰勒展開式,得

其中,O(4)=O(‖(u,v)‖4),又根據

G(φ,0)=τ0(G1,G2)T。

那么

從而由式(25)、(27)和(28)可以得到:

如上表達式可以看出,為了計算g21,需要計算W20(θ)和W11(θ)。

根據

可得

當-1≤θ<0時,

于是結合式(25)和(31),當-1≤θ<0時,有

那么聯立式(30)的第一個方程和式(32)可得

E1exp(2iσ0τ0θ)

同理再聯立式(30)的第二個方程和式(33)可得

令式(30)中θ=0,再利用AU的定義和

分別得到

E1=E11E12和E2=E21E22

其中,

綜上,g21可由計算得到。基于以上分析可以看出,每個gij可以通過參數來確定,于是

定理2 根據系統(3)有如下結論。

(ⅱ)β2決定分歧周期解的穩定性:若β2<0,(β2>0),則分歧周期解是漸近穩定的(不穩定的)。

(ⅲ) T2決定分歧周期解的周期變化:若T2>0,(T2<0),則周期增大(減小)。

3 數值模擬

選取時滯τ作為分歧參數,其中τ=0.11,初值u(x,t)=1+0.1tcos x,v(x,t)=1-0.011cos x,t∈[-0.11,0],x∈[0,3π]。得到模型(3)平衡點(1,1)的穩定性,數值模擬結果見圖1。

(a) u(x,t)數值模擬

由圖1知,當τ∈(0,0.339 3)時,系統(3)的解趨向于平衡點(1,1),此時正平衡點(1,1)是穩定的。

選取時滯τ作為分歧參數,其中τ=0.41,初值u(x,t)=1+0.1cos(4x),v(x,t)=1-0.011cos(x2),t∈[-0.41,0],x∈[0,3π]。那么周期解存在,數值模擬結果見圖2。

(a) u(x,t)數值模擬

由圖2知,當τ在0.339 3的一個很小的右鄰域內時,系統(3)在正常數平衡點(1,1)處產生分歧周期解。