形式各異殊途同歸
——六個角度研究切線問題

盧會玉

(西北師范大學附屬中學,甘肅 蘭州 730070)

高考中,曲線的切線問題幾乎成為必考內容,有時以圓為載體出現在小題,有時在填空題中直接求某函數的切線,有時以關鍵形式出現在大題中.一般情況下,直線與曲線相切會涉及到三個量:直線、曲線、切點;直線與圓相切也涉及到三個量:直線、圓、點.因此,切線問題都有共同的命題方式:知“二”求“一”,即知道其中的兩個量去求另外一個量,雖然考查的知識點和呈現形式不同,但思維方式基本相同.

1 已知曲線的方程、切點坐標求切線方程

例1 曲線y=2sinx+cosx在點(π,-1)處的切線方程為( ).

A．x-y-π-1=0 B．2x-y-2π-1=0

C．2x+y-2π+1=0 D．x+y-π+1=0

解析因為y′=2cosx-sinx,

則y=2sinx+cosx在點(π,-1)處的切線方程為y-(-1)=-2(x-π),即2x+y-2π+1=0．

注本題考查利用導數工具研究曲線的切線方程,滲透了直觀想象、邏輯推理和數學運算素養．采取導數法,利用函數與方程思想解題．學生易在非切點處直接求導數而出錯,首先證明已知點是否為切點,若是切點,可以直接利用導數求解;若不是切點,設出切點,再求導,然后列出切線方程[1]．

例2經過點M(3,0)作圓x2+y2-2x-4y-3=0的切線l,則l的方程為( ).

A．x+y-3=0 B．x+y-3=0或x=3

C．x-y-3=0 D．x-y-3=0或x=3

解析因為x2+y2-2x-4y-3=0,

所以(x-1)2+(y-2)2=8.

當過點M(3,0)的切線存在斜率k,切線方程為y=k(x-3),即kx-y-3k=0.

解得k=1.

即切線方程為x-y-3=0.

因此切線方程為x-y-3=0.故選C.

注本題考查了求圓的切線.本題實際上是過圓上一點求切線,所以只有一條.解答本題時,設直線l存在斜率k,點斜式設出方程,利用圓心到直線l的距離等于半徑求出斜率k,再討論直線l不存在斜率時,是否能和圓相切,如果能,寫出直線方程,綜合求出切線方程.

2 已知曲線的方程、切線方程求切點坐標

例3在平面直角坐標系xOy中,點A在曲線y=lnx上,且該曲線在點A處的切線經過點(-e,-1)(e為自然對數的底數),則點A的坐標是____．

解析設點A(x0,y0),則y0=lnx0.

即x0lnx0=e.

令H(x)=xlnx,當x∈(0,1)時,H(x)<0,當x∈(1,+∞)時,H(x)>0,且H′(x)=lnx+1,當x>1時,H′(x)>0,H(x)單調遞增,注意到H(e)=e,故x0lnx0=e存在唯一的實數根x0=e,此時y0=1,故點A的坐標為(e,1).

例4若曲線y=xlnx上點P處的切線平行于直線2x-y+1=0,則點P的坐標是____．

注導數運算及切線的理解應注意的問題:一是利用公式求導時要特別注意除法公式中分子的符號,防止與乘法公式混淆;二是直線與曲線公共點的個數不是切線的本質,直線與曲線只有一個公共點,直線不一定是曲線的切線,同樣,直線是曲線的切線,則直線與曲線可能有兩個或兩個以上的公共點．

3 已知切線方程、切點坐標求曲線方程

例5已知曲線y=x+lnx在點(1,1)處的切線與曲線y=ax2+(a+2)x+1相切,則a=____.

所以y=x+lnx在點(1,1)處的切線方程為

y=2x-1.

又切線與曲線y=ax2+(a+2)x+1相切,當a=0時,y=2x+1與y=2x-1平行,故a≠0.

所以a=8.

C．(x-5)2+y2=5 D．(x+5)2+y2=5

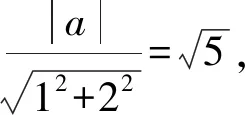
所以圓O的方程為(x+5)2+y2=5．

注切線問題應注意區分曲線在某點處的切線和曲線過某點的切線.曲線y=f(x)在點P(x0,f(x0))處的切線方程是y-f(x0)=f′(x0)(x-x0).求過某點的切線方程,需先設出切點坐標,再依據已知點在切線上求解.

4 曲線的切線與函數性質的綜合問題

例7設函數f(x)=x3+(a-1)x2+ax,若f(x)為奇函數,則曲線y=f(x)在點(0,0)處的切線方程為( ).

A．y=-2xB．y=-xC．y=2xD．y=x

解法1因為函數f(x)=x3+(a-1)x2+ax為奇函數,所以f(-x)=-f(x).

所以(-x)3+(a-1)(-x)2+a(-x)=-[x3+(a-1)x2+ax].

所以2(a-1)x2=0.

因為x∈R,所以a=1.

所以f(x)=x3+x.

所以f′(x)=3x2+1.

所以f′(0)=1.

所以曲線y=f(x)在點(0,0)處的切線方程為y=x．故選D．

解法2因為函數f(x)=x3+(a-1)x2+ax為奇函數,所以f(-1)+f(1)=0.

所以-1+a-1-a+(1+a-1+a)=0.

解得a=1.

所以f(x)=x3+x.

所以f′(x)=3x2+1.

所以f′(0)=1.

所以曲線y=f(x)在點(0,0)處的切線方程為y=x．

5 曲線的切線與兩直線位置關系相結合的問題

解析因為y=ex,所以y′=ex.

所以曲線y=ex在點(0,1)處的切線斜率

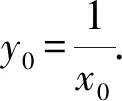
因為x0>0,所以x0=1.

所以y0=1,即點P的坐標是(1,1).

①

②

由①②解得a=-1,b=-2.

所以a+b=-3．

6 圓的切線與圓錐曲線相結合的綜合問題

(1)求橢圓的離心率;

由題意,F(-c,0),則直線l的方程為

7x2+6cx-13c2=0.

由圓心C在直線x=4上,可設C(4,t).

因為OC∥AP,且由(1)知A(-2c,0).

(1)證明:直線AB過定點;

設B(x2,y2),同理可得2tx2-2y2+1=0.

故直線AB的方程為2tx-2y+1=0.

于是x1+x2=2t,x1x2=-1,y1+y2=t(x1+x2)+1=2t2+1,

=2(t2+1).

設d1,d2分別為點D,E到直線AB的距離,則

因此,四邊形ADBE的面積

注以上題型都是圓的切線與圓錐曲線的綜合問題,主要考查橢圓、雙曲線、拋物線的標準方程和幾何性質、直線方程、圓等基礎知識.基本是以圓為主,以圓錐曲線為輔的中檔題目.考查學生用代數方法研究圓錐曲線性質的能力,考查運算求解能力,以及用方程思想、數形結合思想解決問題的能力[2].

事實上,還有相當多的與切線有關的問題本文并未涉及到,但是,各種各樣的切線問題所采用的解決辦法具有相同和相通的地方,在一定程度上也可達到觸類旁通的效果.