基于兩道高考概率題的深入思考

張軍偉

(東北師范大學附屬中學,吉林 長春 130021)

概率是高考重點考查的內容之一,試題常以實際生活問題為背景,與其他知識融合、滲透,情境新穎,充分體現了概率的工具性和應用性.綜合來看,試題難度中等,不僅考查學生的基礎知識和基本技能,更著重考查學生對概率知識的運用能力.在教學中對經典概率高考題進行深度剖析,有利于學生進一步完善解決概率問題的基本思路,優化運算求解過程,提高解題效率.

1 試題呈現

(1)求甲連勝四場的概率;

(2)求需要進行第五場比賽的概率;

(3)求丙最終獲勝的概率.

題2 (2006年高考全國Ⅱ卷第18題)某批產品成箱包裝,每箱5件．一用戶在購進該批產品前先取出3箱,再從每箱中任意抽取2件產品進行檢驗．設取出的第一、二、三箱中分別有0件、1件、2件二等品,其余為一等品．

(1)求抽檢的6件產品都是一等品的概率;

(2)若抽檢的6件產品中有2件或2件以上二等品,用戶就拒絕購買這批產品,求這批產品被用戶拒絕的概率．

2 試題分析

兩道高考題均以生活情境為背景,充分體現了數學的應用性.在知識方面,前者考查相互獨立事件、互斥事件的概率計算,后者考查古典概型、相互獨立事件、互斥事件的概率計算;在能力方面,兩者都深度考查學生分析問題和解決問題的能力,考查層次分明、區分度較高,能使學生充分展示理性思維的廣度和深度;在素養方面,均考查學生數學抽象、邏輯推理、數學運算以及數據分析等數學核心素養[1].

3 解法探究

3.1 題1解析

分析1 首先要弄清楚復雜的賽制,也就是弄清楚一次試驗,可以畫出每場比賽贏者的樹狀圖.

例如,畫出從第一場甲贏開始的各場次贏者的樹狀圖(如圖1),類比得出第一場乙贏的情形.

圖1 分析1圖

從中可以得出:①比賽至少需要進行四場比賽,至多需要進行五場比賽;

②若甲贏,則打四場全贏,或打五場,前四場輸一場,第五場贏,乙贏同理;

③若丙贏,則打四場,第2,3,4場贏,或打五場,從第二場開始的三場比賽輸一場,第五場贏.

所以需要進行第五場比賽的概率為

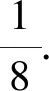
比賽五場結束且丙最終獲勝,則從第二場開始的四場比賽按照丙的勝、負、輪空結果有三種情況:勝勝負勝,勝負空勝,負空勝勝,概率分別為

分析2 由于賽制規定累計負兩場者被淘汰,因此畫出每場比賽負者的樹狀圖更貼合題意.

例如,畫出從第一場甲勝乙開始的各場次勝負的樹狀圖(如圖2),如甲勝乙記作甲>乙,類比得出第一場乙勝甲的情形.

圖2 分析2圖

從中可以得出:①比賽至少需要進行四場比賽,至多需要進行五場比賽;

②某選手負兩場即被淘汰,輪空制下不能連續負兩場,除非已經淘汰了一位選手;

③若甲贏,則打四場,乙、丙各負兩場,或打五場,前四場只能輸一場,第五場贏,乙贏同理;

④若丙贏,則打四場,甲、乙各負兩場,或打五場,從第二場開始的三場比賽只能輸一場,第五場贏.

(2)設A為甲輸,B為乙輸,C為丙輸,則打四場比賽結束有四種情形:BCBC,ACAC,ABAB,BABA,所以需要進行第五場比賽的概率為

(3)設A為甲輸,B為乙輸,C為丙輸,則丙最終獲勝的概率有兩類情形:一類是打四場勝ABAB,BABA;另一類是打五場勝ACBAB,ABCAB,ABACB,BCABA,BACBA,BABCA,ACABB,BCBAA,ABCBA,BACAB.所以丙最終獲勝的概率為

3.2 題2解析

解法1(1)設A=“抽檢的6件產品都是一等品”,則

(2)設B=“這批產品被用戶拒絕”,則

分析2 如果把一次試驗理解成分別從第二、三箱中各任意抽取2件產品,彼此相互獨立,那么就可以結合相互獨立乘法公式及互斥事件加法公式進行計算.

解法2 (1)設A=“抽檢的6件產品都是一等品”,則

(2)設B=“這批產品被用戶拒絕”,則

分析3如果把一次試驗理解成分別從第二、三箱中各任意抽取2件產品,彼此相互獨立,而從每箱取產品第一次、第二次不相互獨立,那么就可以結合條件概率變形公式及互斥事件加法公式進行計算.

解法3 (1)設A=“抽檢的6件產品都是一等品”,則

(2)設B=“這批產品被用戶拒絕”,則

4 變式練習

為了加強學生對某一類問題的掌握,適當地對同類題目加以練習,會起到強化解題思想方法的積極作用.讓學生在親身實踐中尋求變通,悟出其中的來龍去脈,掌握科學的解題規律和法則,進而培養學習的興趣和提高解題的信心.下面給出兩道高考試題供讀者參考.

練習1 (2019年全國Ⅱ卷理18題)11分制乒乓球比賽,每贏一球得1分,當某局打成10∶10平后,每球交換發球權,先多得2分的一方獲勝,該局比賽結束．甲、乙兩位同學進行單打比賽,假設甲發球時甲得分的概率為0.5,乙發球時甲得分的概率為0.4,各球的結果相互獨立．在某局雙方10∶10平后,甲先發球,兩人又打了X個球該局比賽結束．

(1)求P(X=2);

(2)求事件“X=4且甲獲勝”的概率．

解析(1)X=2就是某局雙方10∶10平后,兩人又打了2個球該局比賽結束,則這兩個球均由甲得分,或者均由乙得分.因此P(X=2)=0.5×0.4+(1-0.5)×(1-0.4)=0.5.

(2)X=4且甲獲勝,就是某局雙方10∶10平后,兩人又打了4個球該局比賽結束,且這4個球的得分情況為:前兩球是甲、乙各得1分,后兩球均為甲得分.

因此所求概率為[0.5×(1-0.4)+(1-0.5)×0.4]×0.5×0.4=0.1.

練習2 (2015年湖南理18題)某商場舉行有獎促銷活動,顧客購買一定金額商品后即可抽獎,每次抽獎都從裝有4個紅球、6個白球的甲箱和裝有5個紅球、5個白球的乙箱中,各隨機摸出1個球,在摸出的2個球中,若都是紅球,則獲一等獎;若只有1個紅球,則獲二等獎;若沒有紅球,則不獲獎．

(1)求顧客抽獎1次能獲獎的概率;

(2)若某顧客有3次抽獎機會,記該顧客在3次抽獎中獲一等獎的次數為X,求X的分布列和數學期望．

解析(1)設B1={顧客抽獎1次獲一等獎},B2={顧客抽獎1以獲二等獎},C={顧客抽獎1次能獲獎}.

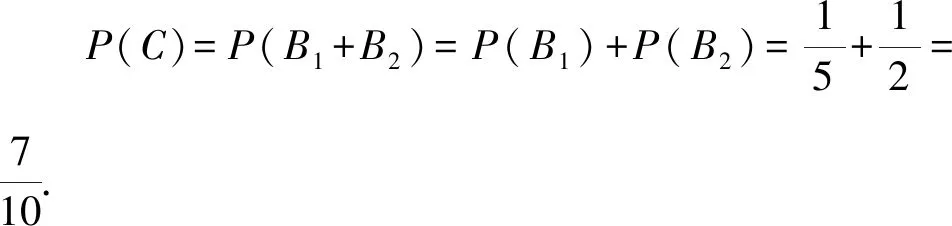
(2)X分布列為

X0123P6412548125121251125

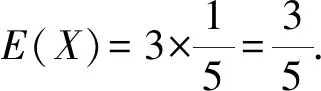
5 教學啟示

通過對兩道高考真題的剖析和解答,我們知道破解這類題型的關鍵是突破試題的情境、理解題意,然后建立正確的概率模型,結合概率計算公式,就能順利求解.我們在教學過程中要注重落實好以下幾方面內容:

5.1 依托實例,完善體系

在概率教學過程中,自始至終都要結合實例展開.教學中應提供豐富的、典型的隨機現象實例,鼓勵學生提出有價值的概率問題,使學生經歷隨機現象—隨機試驗—隨機事件的學習過程,真正搞清楚不同隨機事件的區別與聯系,進而建立對高中階段概率學習的知識體系.體現在解題中,學生往往對試題中涉及的隨機試驗下的隨機事件分析不清楚,不能準確地轉化為相應的概率模型.因此教學中要加強訓練,使學生積累解題經驗,完善概率認知體系,提高分析隨機現象的能力.

5.2 掌握模型,熟練方法

概率的基本性質是概率論的重要理論基礎,它直接給出了概率的計算方法,一是由互斥事件的和事件的概率加法公式直接求,二是由對立事件的減法公式間接求.類型上古典概型的特點是樣本點有限、等可能,相互獨立事件常以概率不變為標志,再結合具體的隨機試驗可以梳理出拋硬幣、擲骰子、取球、比賽等模型.教學時可篩選高考真題講練,引導學生的解題思路——隨機試驗有哪些情形、樣本點是什么、是否有限、是否概率不變,使學生掌握不同事件概率的求解思路以及相關的運算技巧,從而轉化為相應的概率模型進行計算.同時計算較復雜事件的概率,要使學生養成利用二維表或樹狀圖表示試驗結果的好習慣,輔助學生全面地把握題意.

5.3 提煉思想,提高能力

概率是研究隨機現象規律的學科,它為人們認識客觀世界提供了重要的思維模式和解決問題的方法.教師在教學中需要關注:(1)關注學生審題能力,提升學生的數學抽象與直觀想象的數學素養,培養學生發現問題和提出問題的能力;(2)滲透培養數學建模能力,引導學生根據實際問題構建概率模型,分析數據,提升學生數據分析和數學建模能力,培養學生分析問題、解決問題的能力;(3)重視數據計算,規范學生的解題習慣和思維訓練,提升學生的邏輯推理和數學運算能力,培養學生解決問題的能力．概率素養是學生在掌握知識的基礎上,經過反復實踐與反思而后逐漸深化形成,于是在教學中需要滲透思維訓練,培養學生學習概率的興趣和提升其概率素養[2]．

總之,在教學過程中,教師要促進發展學生認識不確定現象的思維模式,使學生學會辯證地思考問題,成為善于認識問題、解決問題的人才.