等效思維下的高中物理解題分析

陳林杰

(福建省連城縣第三中學,福建 連城 366214)

等效思維的正確、靈活應用建立在對物理情境深入理解、物理基礎知識牢固掌握的前提下.為提高學生運用等效思維解題的意識以及應用靈活性,應向學生做好應用示范,多鼓勵學生思考與總結,在頭腦中建立清晰的等效模型,以后解題時能夠迅速找到切入點,合理、正確等效.

1 螺旋運動的等效

多數學生對螺旋運動較為陌生,因涉及到物體在空間上的運動,很多學生搞不清楚運動參數之間的關系,遇到相關問題情境頭腦一片空白.事實上,物體沿著螺旋線做旋轉運動的同時豎直方向上均勻下降,因此,可將物體運動的螺旋軌跡拉直,可將螺旋線等效為斜面,物體的下降高度等效為斜面的高度.物體在螺旋線截面上不停的做圓周運動,拉直后相等于斜面的底邊.在頭腦中建立這一等效模型,便不難解答相關習題.教學實踐中,為降低學生理解難度,可借助多媒體技術動態展示這一等效過程,化抽象為直觀,化形象為具體.

例1如圖1所示,使用光滑鋼絲繞成螺距相同的半徑為R的柱形螺線管.C、D為螺線管的兩端,在同一豎直線上,高度差為h.將一可視為質點的小球套在螺線管上從C點由靜止釋放,運動到D點剛好旋轉n圈,忽略小球運動過程中螺線管的形變,重力加速度為g,則小球從C點到D點的運動時間為____.

圖1 小球在螺旋線上的運動

審題后將小球等效為沿光滑斜面向下運動的情境.根據經驗小球沿斜面運動的加速度a=gsinθ,但是斜面的傾角θ以及斜面的長度s均未知.知道小球轉過的圈數,相等于間接得知斜面底邊的邊長.運用勾股定理以及三角函數便可將上述未知數表示出來,運用運動學公式變可得出結果.

2 單擺運動的等效

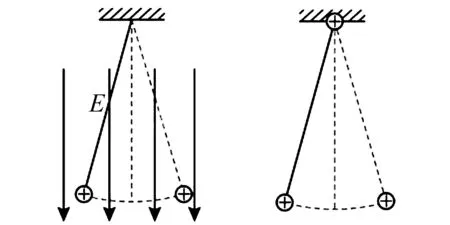
圖2 兩種情境下的單擺運動

3 拋體運動的等效

拋體運動在高中物理中占有重要地位,尤其平拋運動的規律是高中物理測試的熱門考點[2].但是部分習題情境往往突破常規,采用傳統的分析思路難度較大,如使用等效思維可柳暗花明.實踐表明,拋體運動的等效情境分為兩類:一類為反向考慮物體運動,如投飛鏢.一類為水平方向上無能量損失的碰撞.

例3如圖3,將A、B兩光滑高h均為20 m的木板豎直、平行固定在地面上.兩木板的間距d=1 m.從A木板頂端向兩板之間水平拋出速度大小v0=5 m/s可視為質點的彈性小球,忽略空氣阻力以及碰撞的能量損失,小球接觸到地面不再反彈,g取10 m/s2.求(1)小球落地點和A木板的距離;(2)小球和墻面發生m次碰撞時小球下落的高度.

圖3 小球運動情境圖

突破該問題的關鍵在于如何理解無能量損失的碰撞.事實上無能量損失的碰撞是間接告訴物體碰撞后僅改變水平方向速度的方向.碰撞后小球豎直方向的速度不變,而水平方向的速度反向,因此,不管物體碰撞多少次,是和物體做一次平拋運動是等效的.在此基礎上進行整體分析,各種運動參數之間的內在聯系便顯現出來.

4 電阻的等效

電學是高中物理的重要內容,尤其電路的分析以及電學參數的計算,既能考查學生電學規律的理解以及應用靈活性,又能考查學生的運算能力以及運算技巧[3].對于多數電路問題,結合題干運用閉合電路的歐姆定律列出方程便可求出相關參數.但是部分習題設計的較為巧妙,采用常規思路難以作答,遇到這種情況就需要采用等效思維加以解決.其中電阻的等效在解題中較為常用,指將電路中的某一阻值不變的電阻與電源的內阻等效成一個恒定電阻,而后構建方程,如此減少了未知參數的個數,所需的方程數量減少,計算會變得簡單.為使學生認識到這一點,實踐中可為學生講解如下習題,給學生帶來思維上的啟發.

例4如圖4所示電路中電源電動勢為E,內阻為r.兩電壓表的內阻均為RV=6×103Ω,R1=3×103Ω,R2=6×103Ω.當S1閉合S2斷開時,電壓表V1的示數U1=4 V.當S2閉合S1斷開時,電壓表V2的示數U2=7.5 V.求電源電動勢E.

圖4 電路圖

該題出現三個參數,如采用常規思路根據題干描述只能列出兩個物理方程,而且計算較為繁瑣.如將R3和內阻等效成一個電阻,便將該題轉化成了常規問題.列出物理方程,認真計算即可.

5 電場力的等效

將帶電物體放到勻強電場中那么該物體會受到恒定的電場力作用[4].如此便可將其與物體受到的其他恒力合成后等效成一個力,大大簡化分析問題的難度.需要注意的是部分物理習題對電場力進行等效后還需運用相關的物理規律以及經驗,才能找到正確的思路.如分析物體在電場中做豎直平面內的圓周運動時軌道的最低點和最高點和僅受重力下的最低點和最高點是不同的,需基于對圓周運動的深入理解,找到等效最低點和最高點.

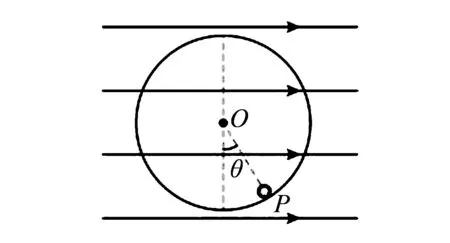
圖5 小球在軌道P點的情境

(1)P點速度v0的大小;

(2)小球做圓周運動經過P點時對軌道的壓力大小.

點評該情境中小球的等效最低點在其靜止時受力平衡的位置.等效最高點是等效最低點關于O點的對稱點.認識到這一點從能量角度入手,構建動能定理方程即可.確定等效最高點是解題的關鍵.

綜上所述,等效思維能創造性地解決很多高中物理問題,使得解題過程更為簡單,解題效率更為高效.教學實踐中應通過理論知識的講解提升學生等效思維應用意識,通過等效思維在解題中的應用展示,使其把握不同物理問題的等效思路以及等效的關鍵,實現應用以及解題水平的提升.