分析思路起點 點亮幾何明燈
——以一次單元評價測試試題為例

桂小兵

(合肥八中教育集團銘傳高級中學,安徽 合肥 231200)

在一次單元評價測試中有兩個題目,學生的思路多樣.有的可以捕捉到初中平面幾何解法的影子,有的是利用高中階段所學向量、函數知識來解決問題,對比這些思路和解法,筆者認為初、高中思維的出發點有些不同,基于這點,在試題評析過程中,通過變式、設問、對比,幫助學生體會不同解法的優勢與弊端,更加透徹地理解此類問題求解方法的本質,逐步滲透高中階段所需具備的向量的基底思想、函數思想,實現思維素養的提升.

圖1 試題1圖 圖2 試題1解析圖

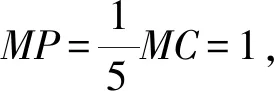
學生將思路1略作修改,得出方案1,如圖3,輔助線作法同思路1.

圖3 追問1圖

在△ACM中利用余弦定理求解CM,在△ACM中利用等面積法求解AQ,再利用CM上點P位置求解PQ,最后在Rt△APQ中利用勾股定理求解AP.

(也有一部分同學給出不求AQ的算法:△ACM中利用余弦定理求解∠ACM,再利用余弦定理求解AP,但運算量較大.)

圖4 追問2圖

學生在方案1的基礎上,給出方案2:

由于△ABC的形狀發生了改變,但相似比未變,所以點P在MC上的相對位置沒有變化.可以先在△ABC中求解∠A的三角函數值,后續思路同思路1,但是學生都給出一個感受,解題中出現了紛繁錯雜的解三角形,邊角求解交替,讓運算過程越來越臃腫,運算量較大.

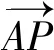
追問3這種基底思路能否解決前面的追問1和追問2呢?

對于追問1,學生在思路2的基礎上,給出方案3:

對于追問2,學生在方案3的基礎上,給出方案4:

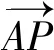
圖5 試題2圖

(1)用α表示OA和OB;

(2)求△AOB面積S的最大值.

學生思路1在閱卷時發現有學生沒有解第一問,而是直接求解了第二問.

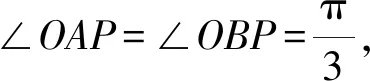
圖6 試題2解析圖

又PA+PB=2m+2n=10,所以m+n=5.

S是關于OA的一個一元二次函數,可求最值.

學生思路2用角度α,結合正、余弦定理表示其他角度、邊元素.

又AP+BP=(1+tanα)·BP=10,

追問線段OP的最小值能否求解?

學生在思路1基礎上,給出方案:

學生在思路2基礎上,給出方案: