一道診斷性試題的多解探究及溯源推廣

劉 艷

(四川省名山中學,四川 雅安 625100)

高考數學對圓錐曲線的考查一直體現基礎與綜合并存,應用與創新充分銜接的特點,每道圓錐曲線題都值得我們去深入探究和思考,由此引發的很多高考改編題也耐人尋味.本文以一道診斷性試題為例,對此題展開多解探究,并對問題進行溯源和推廣,得到了一般性結論,最后對解析幾何教學中如何提升學生核心素養方面進行反思,以期能在教學實踐中更好地推進新高考改革.

1 題目呈現

(1)求橢圓C的標準方程;

2 多解探究

2.1 第(1)問解析

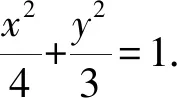
2.2 第(2)問解析

2.2.1根與韋達合理搭橋,慧眼識金巧消元

解法1 由題意直線l的斜率不為零,故設其方程為x=my+4.

(3m2+4)y2+24my+36=0.

①

由Δ>0,得m2>4.

設A(x1,y1),B(x2,y2),則由韋達定理有

易知F(1,0),所以

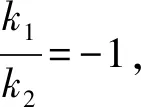
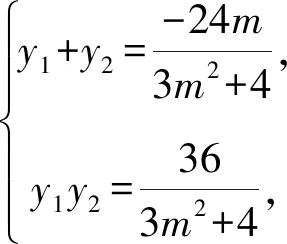
解法5由題意直線l的斜率存在且不為零,故設其方程為y=k(x-4).

(3+4k2)x2-32k2x+64k2-12=0.

又F(1,0),所以

2.2.2數形結合巧移圖形,齊次轉化構斜率

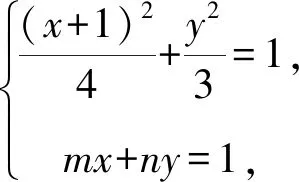
3x2+6x(mx+ny)+4y2-9(mx+ny)2=0.

整理,得(3+6m-9m2)x2+(6n-18mn)xy+(4-9n2)y2=0.

2.2.3活用條件結論齊構造,高屋建瓴妙解題

整理,得12(x-1)2+(12-3m2)y2=0.

兩邊同時除以(x-1)(x≠1),得

3 溯源推廣

3.1 試題溯源

近年來,很多高考解析幾何題均以高等幾何中的有關概念和性質為指導,本題追溯到高等幾何中的極點、極線內容,下面給出相關概念和定理.

定義1點P在圓錐曲線外,過點P作曲線的兩條割線,分別交曲線于A,B和C,D,設AC∩BD=X,AD∩BC=Y,則直線XY為點P的極線(如圖1).

圖1 定義1圖 圖2 定義2圖

定義2點P在圓錐曲線內,過點P作兩條直線,分別交曲線于A,B和C,D,設AC∩BD=X,AD∩BC=Y,則直線XY為點P的極線如圖2所示.

定理1 (配極原則) 如果點P的極線通過點Q,則點Q的極線也通過點P.

圖3 定義1圖

3.2 推廣探究

通過以上極點極線知識分析,進一步推廣得到如下結論:

4 解題反思

4.1 多解探究,積累通性通法

通過一題多解,引導學生積累解決一類問題的通性通法,達到“解一題,會一法,通一類”的學習目的.本題中第(2)問很多同學知道用韋達定理來解決問題,但卻無法整體找到兩根之和與兩根之積之間的關系,橋梁建立不起來,最后無計可施只能到韋達定理這一步為止了.但如果想到借助求根公式與韋達定理同時搭橋,本題也能迎刃而解.如果能再借助圖形分析猜想直線AF,BF的傾斜角互補,再驗證一下它們的斜率之和,本題也能順利解決.所以,在圓錐曲線解題中,韋達定理雖然經常用,但很多學生只通其一不通其二,在遇到這種所謂的非對稱結構運算問題時,學生如果沒有經驗,考試時是難以過關的.而齊次構造是處理斜率問題的通性通法,如果學生能靈活處理好條件結論中的代數關系,此題也能很好地解決[2].

4.2 把握本質,重視思想運用

素養的培養更重要的是要注重數學思維的培養,領悟知識背后的本質,重視知識背后的數學思想的滲透.高中解析幾何內容兼具幾何與代數雙重特性,在教學時應不拘泥于套路形式,應突出和把握問題的本質.比如本題中韋達定理學生學得太死了,導致學生感覺用韋達定理解決不了這個問題,其實本題運用的本質是消元和轉化思想,如何消元,如何將已知轉化出來為我所用或者將未知轉化為已知,處理方法有很多種,思路打開了,問題也就能解決了.