維度和壓強對顆粒體系振動態密度的影響
李歌天,曾援,張波,張國華
(北京科技大學數理學院,北京 100083)
在自然界中,存在著大量的顆粒物質,它有著與氣體、固體和液體所不同的特點和性質,顆粒物質作為一種復雜的離散體系,無序性是它的重要特點[1]。想用現今的理論知識對顆粒物質進行完整描述是非常困難的,這也是研究顆粒體系的意義所在。理論表明,晶體材料的低頻振動為長波平面波,其低頻態密度(density of states,DOS)滿足D(ω)~ωd,其中,d為維度,D(ω)為低頻態密度,ω為振動圓頻率。但是非晶材料的低頻態密度出現大量偏離德拜預測的額外振動模式,這些額外模式對非晶材料的力學性質有非常大的影響。因此,研究無序材料振動態密度對其力學行為的影響,一直是材料力學的研究熱點之一。近年來,許多學者對顆粒體系進行了試驗和數值模擬,以探究它的振動特性、堵塞、耗散和顆粒鏈的尺寸效應[2-5]。如顆粒體系的振動態密度、態密度圖像、堵塞相圖以及臨界點J處的特征等。文獻[6-8]對顆粒物質的振動態密度進行了研究,將Hessian矩陣的簡正模式分析法用于研究無序顆粒體系(如液體、玻璃介質等)的振動態密度。Zhang等[9]研究了無序程度對玻璃狀固體振動態密度的影響,發現當二維顆粒填料從晶體結構逐漸調整為多晶結構乃至非晶結構時,玻色峰和van-Hove singularity奇異性在多晶體中很好地分離,且當無序性足夠高時van-Hove singularity奇異性消失。Krishnan等[10]用Hessian矩陣法研究了剪切無序固體的非德拜低頻振動,發現構型選擇對于低頻態密度的重要影響,并且發現當接近塑性事件時,Hessian矩陣的最小本征值到達一個普適的分布。Wang等[11]研究了三維玻璃材料的低頻態密度,發現當頻率低于第一聲模式時三維玻璃材料的低頻態密度D(ω)~ωβ,β<4,β為冪指數,對于不同體系取不同的數值。Dale等[12]研究了超均勻(hyperuniform)三維球形顆粒填料的振動態密度,發現超均勻球形顆粒填料在低頻下不存在態密度隨頻率的標度,而是在有限頻率下的突然低頻截止,形成了大約零頻率的聲子帶隙。在這個間隙上方,存在一個離散的模式帶。然而,目前關于不同維度和壓強下顆粒材料低頻態密度的系統研究尚鮮見報道。
為此,運用離散元法(discrete element method,DEM),借助PFC軟件生成不同維度下,壓強P處于0.1~10 000 Pa的范圍內,由2 048個無摩擦顆粒組成的顆粒體系數值模型,再運用MATLAB軟件,通過Hessian矩陣的簡正模式分析法,對數值模型進行計算并總結其規律。為進一步理解維度、壓強對顆粒材料的低頻力學性質的影響有幫助。
1 顆粒物質
顆粒物質指的是離散且半徑大于0.5 μm,間隙液體的黏性較低,并且飽和度在1以下的大量固體顆粒,在相互作用下組成的復雜體系。它廣泛存在于自然界中,在日常生活、生產等各個方面中都有所涉及[13]。
顆粒物質的性質及其豐富[14],如在沒有外力作用時,顆粒體系的狀態與固體的狀態相似,有外力作用時,顆粒物質會發生流動,此時它的狀態會更接近氣體和流體[15]。該體系屬于宏觀,但又和微觀相聯系,屬于固體,但又和流體和氣體相關,具有較強的綜合性,對它的研究可以涉及生活的各個方面。作為一種具有代表性的無序系統,顆粒體系的振動態密度與非晶體材料具有類似的特點,比如說存在許多低頻軟模式[16]、Boson峰和局域化模式等[17]。
2 數值模擬
2.1 樣品制備
用PFC2D分別生成包括2 048個光滑圓盤顆粒的一維顆粒鏈和處于2 m×2 m方盒子中的二維顆粒圓盤填料,采用周期性邊界條件并忽略重力的影響。采用PFC3D軟件在2 m×2 m×2 m立方盒子中生成了包括2 048個光滑球形顆粒的三維顆粒填料。
具體顆粒填料的產生方式如下:首先,在選定的邊界內隨機產生2 048個半徑很小的顆粒(此時顆粒之間重疊量很小,可認為處于松弛狀態)。然后,增大顆粒半徑,使得體系壓強達到2×104Pa,采用共軛梯度法使得體系處于能量極小的狀態,生成初始壓強的顆粒填料。為了得到不同壓強下的顆粒填料,通過逐漸減小顆粒半徑的方法進行卸載,使得體系壓強分別達到10 000、1 000、100、10、1、0.1 Pa。填料穩定的判據是經過1 000個循環前后系統的能量差的比例小于1×10-15填料穩定后,將各個顆粒填料的信息保存到文件。對每個壓強都隨機生成了10個位形,所涉及的物理量都是這10個位形的平均值。
2.2 態密度的求解
體系振動模式及振動態密度可通過求解下列久期方程來實現。
|F-ω2I|=0
(1)
式(1)中:I為單位矩陣;ω為振動圓頻率;F為Hessian矩陣。
(2)
光滑圓盤顆粒之間的相互作用為單邊線性彈簧勢,一般情況下,顆粒i和j的相互作用勢可表示為
(3)
“區塊鏈”已成為信息技術應用行業的熱門詞,區塊鏈技術應用也得到了國家在信息技術領域的關注和重視,一方面加大對首次幣發行(Initial Coin Offering,ICO)項目的監管,另一方面積極推動國內區塊鏈在相關領域的標準化制定及產業化發展等研究工作[1]。從“互聯網+”逐步上升到“區塊鏈+”。無論從社會價值還是投資價值投資考慮,在這股熱潮之中,最終需要沉淀和落地的是“區塊鏈+實際場景”的應用,只有先進的技術應用到具體項目才能擁有可持續的生命力,才能創造出真正的價值[2]。
(4)
式(4)中:ki和kj分別為顆粒i和j的法向接觸剛度系數。
光滑球形顆粒i和j的相互作用為Hertz勢,可表示為
(5)
(6)
對于各向同性材料,E=2G(1+ν),其中G為剪切模量。

3 結果與討論
3.1 一維顆粒鏈的振動態密度
在一維條件下,選取若干個一維顆粒鏈,并對所有結果進行了平均計算,運用Hessian矩陣求解穩定狀態下harmonic接觸的一維顆粒鏈的振動態密度,并繪制態密度D(ω)~ω曲線,如圖1所示。
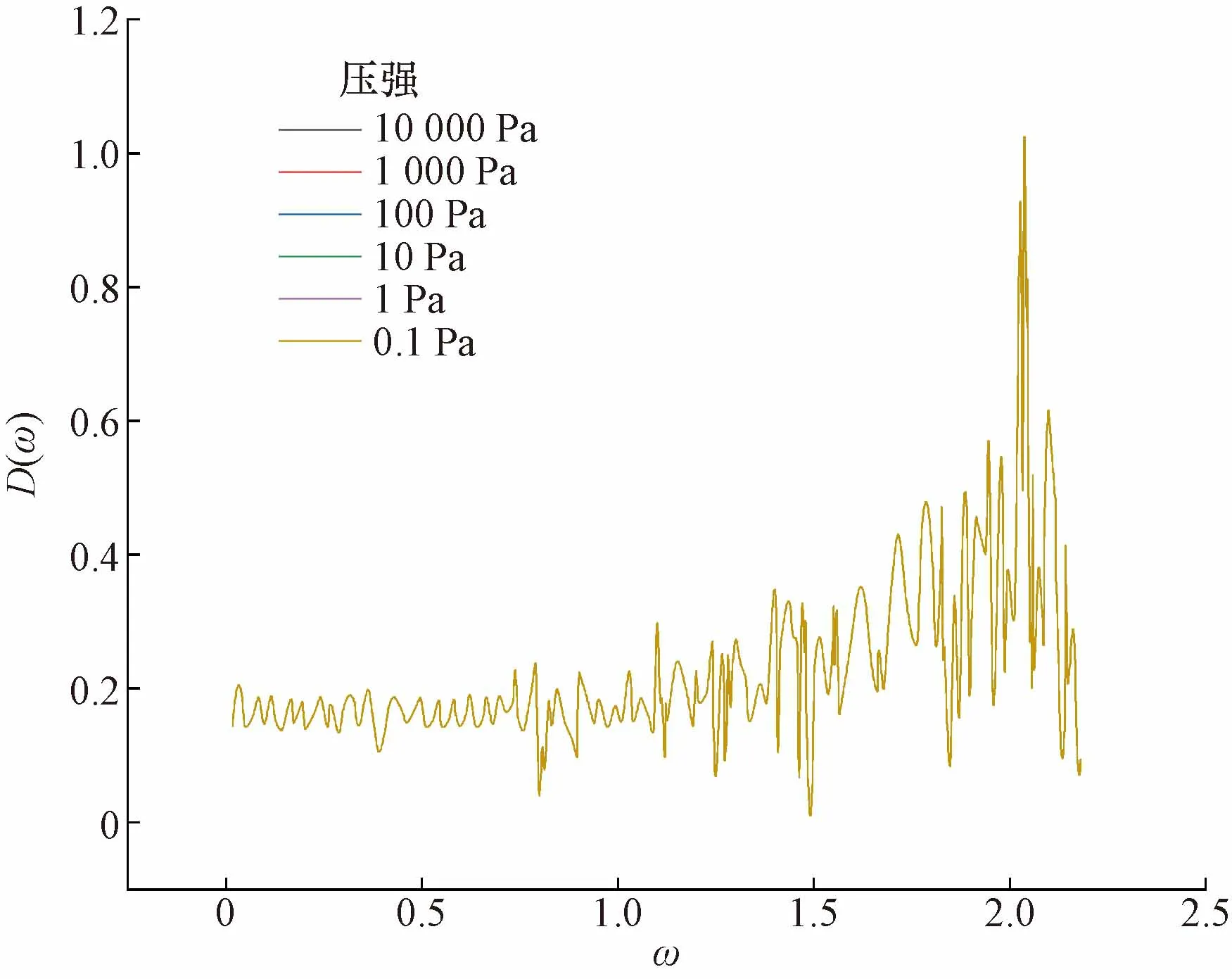
圖1 Harmonic接觸的一維顆粒鏈態密度圖Fig.1 Density of states curve of one-dimensional particle chain with harmonic contact
從圖1可以看出,在不同壓強條件下,由2 048個顆粒組成的一維無摩擦顆粒鏈體系的振動態密度完全一致。一維顆粒體系的振動態密度在0.1~10 000 Pa的壓強下時,其振動態密度曲線不受壓強影響。且曲線在ω的值較小時,曲線振蕩頻率較小且較為穩定,在ω逐漸增大后,曲線振蕩幅度變大,且D(ω)的平均值隨著的增大呈逐漸上升趨勢,將ω的值和D(ω)都用對數坐標進行表示時,更能體現這一特點。
如圖2所示,不同壓強的曲線完全重合,即壓強變化與態密度曲線的變化無關,并且在低頻區域,態密度曲線趨近于一條直線。根據德拜理論,D(ω)~ωγ,γ=d-1。其中,d為體系維度,當d=1時,γ=d-1=0。因此,在一維條件下,D(ω)~ω0,反映在曲線上即在低頻區域,態密度曲線趨近于直線。可以看出,圖2的曲線符合德拜理論的預測。

圖2 雙對數坐標下的harmonic接觸的一維顆粒鏈態密度圖Fig.2 One-dimensional particle chain of the density of states for harmonic contact in double logarithmic coordinates
3.2 二維顆粒體系的振動態密度
首先用PFC2D軟件在一個2 m×2 m方盒子中生成顆粒半徑在0.009~0.011 m平坦分布的2 048個光滑二維顆粒填料。x、y方向均采用周期性邊界條件。此時體系中顆粒所處位置完全是隨機的,且顆粒間沒有任何重疊,體系處于完全松弛的狀態。接著,使顆粒半徑逐漸增大,直至體系的壓強到達一個固定值(P=1 000 Pa)。然后采用共軛梯度法使顆粒體系卸載到實驗所需要的一系列壓強值。隨機改變初始樣品中顆粒的位置,重復上述過程,從而制備若干壓強相同二維顆粒填料。通過Hessian矩陣的簡正模式分析法得到該壓強下二維顆粒填料的平均振動態密度。圖3為計算得到的壓強分別為0.1、1、10、100、1 000、10 000 Pa的二維顆粒體系的態密度曲線。

圖3 二維無摩擦顆粒體系的振動態密度Fig.3 Vibronic density of states a two-dimensional frictionless particle system

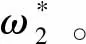

圖4 雙對數坐標下二維顆粒體系的態密度Fig.4 Vibronic density of states a two-dimensional frictionless particle system in double logarithmic coordinates


圖5 雙對數坐標下二維顆粒體系過渡頻率隨壓強P的變化關系Fig.5 Variation of the two-dimensional system with pressure P in double logarithmic coordinates
3.3 三維顆粒體系的振動態密度
首先用PFC3D軟件在2 m×2 m×2 m立方體盒子中生成顆粒半徑在0.009~0.011 m平坦分布的2 048個光滑三維球形顆粒填料。x、y、z方向均采用周期性邊界條件。接著,使顆粒半徑逐漸增大,直至體系的壓強到達一個固定值(P=1 000 Pa)。然后采用共軛梯度法使顆粒體系卸載到實驗所需要的一系列壓強值。隨機改變初始樣品中顆粒的位置,重復上述過程,從而制備若干壓強相同三維顆粒填料。通過Hessian矩陣的簡正模式分析法得到該壓強下的平均振動態密度。圖5為計算得到的壓強分別為0.1、1、10、100、1 000、10 000 Pa的三維顆粒體系的態密度曲線。
由圖6可知,對于三維無摩擦顆粒體系,每個一壓強下的振動態密度曲線都呈現一個明顯的峰值,D(ω)先隨著ω的增大而增大,在到達峰值后隨著ω的增大而減小;而在不同壓強條件下,壓強越大,其態密度曲線相比于壓強較小條件下的態密度曲線,顯得更為“矮胖”,曲線底部的寬度增大,D(ω)的最高峰峰值越小,且峰值越靠右,即在取到峰值時,ω的值越大。

圖6 雙對數坐標下三維顆粒體系的態密度Fig.6 Vibronic density of states a three-dimensional frictionless particle system

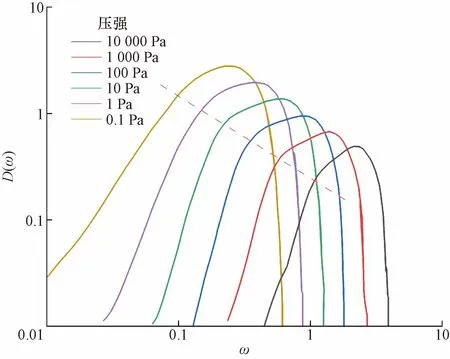
圖7 雙對數坐標下三維顆粒體系的態密度Fig.7 Vibronic density of states a three-dimensional frictionless particle system in double logarithmic coordinate

圖8 雙對數坐標下三維顆粒體系隨壓強P的變化關系Fig.8 Variation of the three-dimensional system with pressure P in double logarithmic coordinates
4 結論
采用離散元法生成了不同維度和壓強下的顆粒體系,通過Hessian矩陣簡正模式分析法計算得到顆粒體系的態密度,進一步研究了維度和壓強對顆粒體系振動態密度的影響,得出以下結論。
(1)一維條件下,一維無摩擦顆粒鏈的態密度曲線不隨壓強的變化。在低頻處,態密度曲線幾乎不隨頻率變化;在高頻率處,態密度曲線隨著頻率增大呈現振蕩上升趨勢。



