附加阻尼影響下的極地破冰船波浪增阻研究

陳超?張偉?劉亞東

摘要：考慮到極地破冰船典型的破冰型船艏會(huì)對(duì)大洋航行阻力性能產(chǎn)生不利的影響，進(jìn)而對(duì)其波浪增阻性能展開研究。基于三維非線性勢(shì)流理論，以線性加平方的阻尼模型等效考慮船體黏性橫搖阻尼，研究了極地破冰船在不同浪向下波浪增阻特性。進(jìn)一步地，考慮減搖裝置帶來的等效附加阻尼，研究附加阻尼對(duì)艏斜浪下波浪增阻的影響規(guī)律，分析附加阻尼對(duì)波浪中阻力時(shí)歷曲線的各階幅值的影響。研究發(fā)現(xiàn)，附加阻尼對(duì)部分海況條件下波浪增阻有減弱作用，降低了船體阻力時(shí)歷曲線的非線性，對(duì)極地破冰船大洋航行起到改善作用。關(guān)鍵詞：極地破冰船；非線性勢(shì)流方法；橫搖阻尼；波浪增阻

中圖分類號(hào)：U 674.31

文獻(xiàn)識(shí)別碼：A

0 引 言

從我國對(duì)極地破冰船的實(shí)際需求出發(fā)，從母港出發(fā)至極地的航行距離較長，極地破冰船不僅需要強(qiáng)大的破冰能力，還需要具備良好的大洋航行阻力性能。極地破冰船和常規(guī)船型在型線特征上存在諸多差異，其有利于破冰性能的船體型線可能會(huì)對(duì)阻力性能造成不利的影響，因此研究極地破冰船在大洋航行中的波浪增阻性能對(duì)船型優(yōu)化設(shè)計(jì)具有重要意義。

實(shí)驗(yàn)是研究波浪增阻性能的重要手段，船舶水動(dòng)力學(xué)會(huì)議論文集[1-2]提供了包括了KVLCC2船、KCS船等船型的波浪增阻數(shù)據(jù)，詳細(xì)地介紹了試驗(yàn)的參數(shù)和試驗(yàn)結(jié)果。黏性CFD方法可以較為準(zhǔn)確地求解規(guī)則波中波浪增阻[3]，并描述流體的物理現(xiàn)象，但這些計(jì)算一般會(huì)耗費(fèi)大量的計(jì)算資源。基于勢(shì)流理論方法預(yù)報(bào)波浪增阻計(jì)算效率高，預(yù)報(bào)結(jié)果較為準(zhǔn)確。在切片理論方法中，可以采用近場(chǎng)法和遠(yuǎn)場(chǎng)法確定速度勢(shì)進(jìn)而求解波浪引起的船舶運(yùn)動(dòng)和波浪增阻。三維面元法能夠更完善地考慮船體幾何和船型參數(shù)的影響，因而得到了有效的應(yīng)用[4-7]。

一般情況下，船舶在迎浪中的波浪增阻預(yù)報(bào)研究最為重要，實(shí)驗(yàn)研究Valanto[8-9]表明波浪入射角也會(huì)對(duì)波浪增阻產(chǎn)生一定的影響，由于船舶在斜浪中的運(yùn)動(dòng)響應(yīng)更為復(fù)雜，其預(yù)報(bào)難度也迅速提升，Liu等[10]擴(kuò)展了遠(yuǎn)場(chǎng)法預(yù)測(cè)斜浪中船舶的波浪增阻，Zhan等[11]使用CFD方法對(duì)斜浪中的波浪增阻進(jìn)行了數(shù)值模擬并取得了較理想的結(jié)果。同時(shí)，Graf等[12]基于非線性切片理論對(duì)游艇的波浪增阻性能展開了研究，發(fā)現(xiàn)安裝減搖鰭可以減小波浪增阻，但并未對(duì)這一現(xiàn)象進(jìn)行深入研究。

為此，研究極地破冰船在典型海況下的波浪增阻性能，特別是斜浪環(huán)境條件下的波浪增阻性能，對(duì)于深入掌握極地破冰船的阻力性能有重要價(jià)值。在綜合考慮計(jì)算精度和求解時(shí)間的條件下，本文將基于三維非線性時(shí)域勢(shì)流方法求解波浪增阻，并研究橫搖阻尼對(duì)波浪增阻的影響。

1 理論介紹

1.1非線性時(shí)域勢(shì)流理論

假定流體無粘、不可壓縮、流動(dòng)無旋，用速度勢(shì)φ描述流體運(yùn)動(dòng)，勢(shì)流中的線性偏微分方程和控制方程表示為：

在自由面上，應(yīng)用完全非線性邊界條件：

物質(zhì)導(dǎo)數(shù)的定義為：

在流體中，船體表面不可穿透，船體表面某處的速度與該處流體的法向速度相等：

式中，n是船體表面的單位法向量；u和ω是船體的線速度和角速度；r是指向旋轉(zhuǎn)中心的向量。

計(jì)算域底部不可穿透條件：

基于邊界元法（BEM）和混合歐拉拉格朗日（MEL）方法，聯(lián)立求解上述方程，得到速度勢(shì)的分布，再根據(jù)伯努利方程中速度與壓力的關(guān)系，求解受力和運(yùn)動(dòng)。

非定常伯努利方程如下：

將瞬時(shí)濕表面上的壓力積分，獲得作用在船體上的力和力矩：

式中，為重心的線加速度；I 為船體慣性矩；為角加速度；p為船體表面的壓力；Sb為船體濕表面積。

1.2波浪增阻系數(shù)

波浪增阻等于船舶在波浪和靜水中阻力的差值，為便于進(jìn)行對(duì)比分析，使用無因次的波浪增阻系數(shù)：

式中，RAW是在規(guī)則波中的平均波浪增阻；RW代表船舶在波浪中的總阻力；RC代表靜水中的阻力；ρ是流體密度；g是重力加速度；ζa是規(guī)則波的波幅，等于波高的一半；B是船寬；Lpp是垂線間長。

基于勢(shì)流理論方法求解船舶在波浪中的波浪增阻時(shí)做了一個(gè)簡(jiǎn)單的假定，近似地認(rèn)為船舶在靜水中的摩擦阻力和波浪中的平均摩擦阻力是相等的。

1.3橫搖阻尼

非線性時(shí)域勢(shì)流方法在求解船舶在波浪中的運(yùn)動(dòng)時(shí)沒有考慮黏性的影響，而橫搖運(yùn)動(dòng)受到黏性的影響較大，在橫搖運(yùn)動(dòng)方程中體現(xiàn)為阻尼項(xiàng)，需要采取有效手段考慮黏性的影響以提高模擬的準(zhǔn)確性。

基于線性加平方的阻尼模型，代入到非線性時(shí)域勢(shì)流方法的數(shù)學(xué)模型中，有助于準(zhǔn)確地模擬船舶在波浪中的運(yùn)動(dòng)響應(yīng)和遭受的波浪載荷。在線性加平方的阻尼模型中，橫搖阻尼B44可以表示為：

其中，B1、b1分別為線性阻尼和線性阻尼系數(shù)，B2、b2為二階阻尼和二階阻尼系數(shù)，Bcrit為臨界阻尼。

2 數(shù)值計(jì)算結(jié)果分析

2.1 船體幾何模型

本文以某型極地科考破冰船為研究對(duì)象，其主要參數(shù)見表1，該船典型的型線特征為勺型艏、傾斜艏柱和圓潤型船艉，船體示意如圖1所示。

2.2? 數(shù)值計(jì)算設(shè)置

定義波浪前進(jìn)方向和船艏方向的夾角為浪向角χ，迎浪狀態(tài)時(shí)，χ等于180°，除迎浪海況外，斜浪模擬時(shí)浪向角分別設(shè)定為165°、150°和135°。模擬時(shí)的波長比（λ /L）范圍為0.4～2.6，波高為0.012倍的垂線間長。

通過三維勢(shì)流求解器SHIPFLOW進(jìn)行數(shù)值計(jì)算，將自由面和船體表面離散，在平衡計(jì)算時(shí)間和精度的情況下所劃分中等尺度網(wǎng)格，網(wǎng)格如圖2所示，總計(jì)1萬余網(wǎng)格。

極地破冰船船型較為特殊，裸船體橫搖阻尼較小，為了研究附加阻尼對(duì)船體波浪增阻的影響，以減搖水艙為船體減搖裝置，該裝置在五級(jí)海況下的減搖效果可達(dá)30%～40%，在這里將其等效為附加阻尼代入到基于勢(shì)流理論的數(shù)值計(jì)算中。橫搖阻尼系數(shù)通過基于黏性CFD數(shù)值模擬技術(shù)的自由橫搖衰減曲線獲得，該方法的有效性已經(jīng)在多種船型上得以驗(yàn)證[13]，數(shù)值模擬獲得的自由橫搖運(yùn)動(dòng)曲線如圖3所示。

2.3 不同浪向下的波浪增阻變化規(guī)律

圖4為不同浪向下波浪增阻系數(shù)隨波長的變化情況，圖中給出了迎浪、正橫浪和艏斜浪下的波浪增阻結(jié)果。正橫浪的波浪增阻系數(shù)與迎浪和艏斜浪的有明顯區(qū)別，在正橫浪海況下，不同波長下的波浪增阻都接近于0。

不難發(fā)現(xiàn)，迎浪下會(huì)產(chǎn)生最嚴(yán)重的波浪增阻，因此之前的很多研究也都集中于船體迎浪下的波浪增阻性能。當(dāng)波長比大于1時(shí)，改變浪向角可以有效地降低波浪增阻，起到改善船體航行性能的作用。艏斜浪135°下的波浪增阻系數(shù)已經(jīng)較小，應(yīng)當(dāng)給予迎浪至艏斜浪135°范圍內(nèi)的波浪增阻性能關(guān)注。

從方形系數(shù)對(duì)波浪增阻的影響來看，方形系數(shù)較大的船型波浪增阻會(huì)更大[14]，極地破冰船方形系數(shù)為0.67，總體上看在波浪中航行時(shí)容易獲得更多的波浪增阻。此外，方形系數(shù)較大的船型，其波浪增阻峰值對(duì)應(yīng)的波長比也越大，極地破冰船波浪增阻的峰值則出現(xiàn)在波長比1.2附近。可以推測(cè)，盡管極地破冰船沒有球鼻艏，但是較大的方形系數(shù)降低了垂蕩和縱搖的自然頻率，從而增大了波浪增阻峰值對(duì)應(yīng)的波長比。

如圖4所示，隨著波浪從迎浪180°向艏斜浪135°變化，波浪增阻峰值逐漸減弱，峰值對(duì)應(yīng)的波長比從1.2逐漸轉(zhuǎn)移至0.8附近，這是波浪入射角度引起遭遇頻率變化導(dǎo)致的。浪向角165°下的波浪增阻和迎浪結(jié)果較為接近，浪向角度較小的變化對(duì)波浪增阻的影響較小。當(dāng)浪向角為165°且波長比大于1時(shí)，波浪增阻隨著波長比的增大而逐漸減小。艏斜浪135°的波浪增阻系數(shù)峰值大約為迎浪波浪增阻系數(shù)峰值的一半。

按船舶在波浪中航行時(shí)周圍的流動(dòng)現(xiàn)象和阻力增加的原因來分類，波浪增阻可分為輻射增阻和繞射增阻。輻射增阻由總的波浪增阻減去繞射增阻，在數(shù)值模擬中固定船體模型，可以近似地獲得繞射增阻，圖5為設(shè)計(jì)航速下迎浪航行時(shí)繞射增阻和輻射增阻成分隨波長的變化特征。

當(dāng)波長較短時(shí)，此時(shí)船體的運(yùn)動(dòng)響應(yīng)幅值較小，輻射運(yùn)動(dòng)消耗的能量較小，繞射增阻是極地破冰船波浪增阻的主要成分，繞射增阻與總的波浪增阻差異較小。輻射增阻和船體的運(yùn)動(dòng)關(guān)系密切，在短波區(qū)域，輻射增阻隨波長的減小而減小，當(dāng)波長比大于2時(shí)，船體與波面的相對(duì)運(yùn)動(dòng)較小，輻射增阻成分較小且接近于0。繞射增阻隨波長的變化相對(duì)較小，但輻射增阻隨波長的變化較為明顯，輻射增阻和波長的關(guān)系近似一個(gè)單峰函數(shù)，在波長比1.2附近出現(xiàn)峰值。當(dāng)遭遇頻率靠近共振頻率時(shí)，船體與波浪的相對(duì)運(yùn)動(dòng)最為明顯，輻射增阻在總波浪增阻中占比大于繞射增阻成分的占比。

繞射增阻隨波長的變化相對(duì)較小，當(dāng)波長較短時(shí)，此時(shí)船體的運(yùn)動(dòng)響應(yīng)幅值較小，輻射運(yùn)動(dòng)消耗的能量較小，繞射增阻是極地破冰船波浪增阻的主要成分，繞射增阻與總的波浪增阻差異較小。輻射增阻和船體的運(yùn)動(dòng)關(guān)系密切，隨波長的變化較為明顯。輻射增阻和波長的關(guān)系近似一個(gè)單峰函數(shù)，在波長比1.2附近出現(xiàn)峰值；當(dāng)遭遇頻率靠近共振頻率時(shí)，船體與波浪的相對(duì)運(yùn)動(dòng)最為明顯，輻射增阻在總波浪增阻中占比大于繞射增阻成分的占比；在短波區(qū)域，輻射增阻隨波長的減小而減小，主要是由于垂向運(yùn)動(dòng)也隨著波長減小而減小；當(dāng)波長比大于2時(shí)，船體與波浪處于相對(duì)靜止的狀態(tài)，輻射增阻成分較小且接近于0。

2.4 阻尼對(duì)艏斜浪下波浪增阻影響

圖6為裸船體和附加阻尼2種模式下極地破冰船艏斜浪的波浪增阻隨波長變化對(duì)比情況，在附加阻尼的作用下，船體運(yùn)動(dòng)響應(yīng)發(fā)生了變化，進(jìn)而影響了波浪增阻。可以看到，艏斜浪150度和135度下附加阻尼的波浪增阻峰值略有降低，部分波長區(qū)域下的波浪增阻也有所降低。

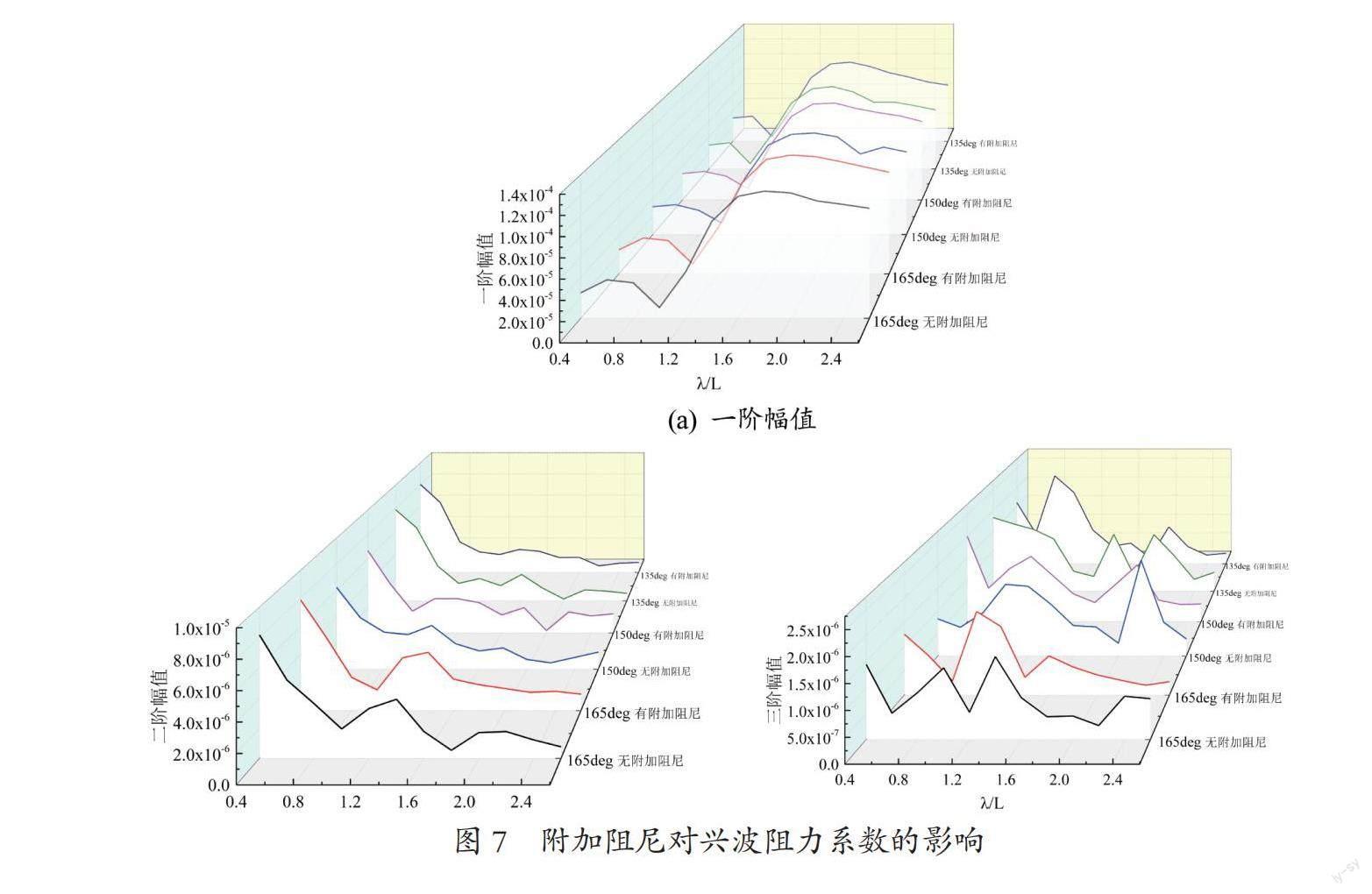
僅從波浪增阻系數(shù)進(jìn)行附加阻尼的影響分析還不夠全面，為此，提取了阻力時(shí)歷曲線的各階幅值進(jìn)行分析，如圖7所示為附加阻尼對(duì)興波阻力系數(shù)的影響。在附加阻尼的作用下，阻力曲線的一階幅值未有明顯的變化，二階幅值和三階幅值有所減弱，在一定程度上改善了受力的非線性，船體遭受的波浪作用力更加均衡。

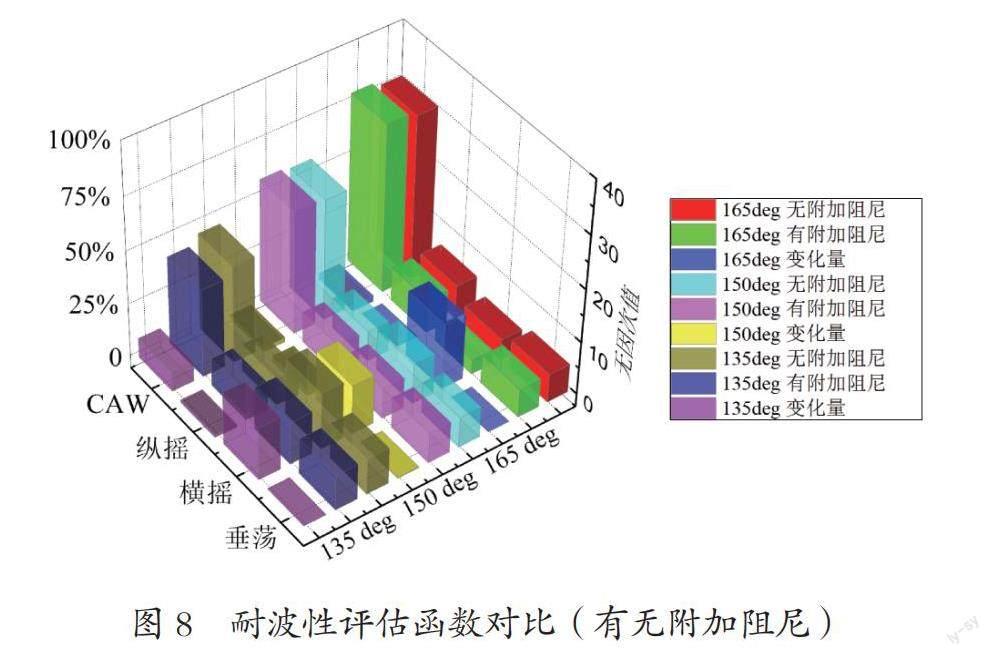
聯(lián)合附加等效阻尼對(duì)運(yùn)動(dòng)響應(yīng)的影響，繪制成圖8所示的耐波性評(píng)估函數(shù)對(duì)比圖，耐波性評(píng)估函數(shù)為頻率與對(duì)應(yīng)響應(yīng)函數(shù)曲線圍成的面積。艏斜浪135°下，在垂蕩和縱搖運(yùn)動(dòng)變化較小的情況下，橫搖運(yùn)動(dòng)的減弱也有效地降低了波浪增阻，艏斜浪165°和150°下，橫搖運(yùn)動(dòng)的減弱并未對(duì)波浪增阻產(chǎn)生明顯的變化，附加等效阻尼在改善船體運(yùn)動(dòng)響應(yīng)的同時(shí)還對(duì)降低波浪增阻起到了有利的影響。從船舶橫搖運(yùn)動(dòng)姿態(tài)和波浪增阻的關(guān)系來說，極地破冰船艏斜浪135°下的橫搖運(yùn)動(dòng)響應(yīng)較為明顯，此時(shí)通過減小橫搖運(yùn)動(dòng)響應(yīng)幅值將有利于降低波浪增阻。

3 結(jié) 論

本文基于三維非線性勢(shì)流理論求解了極地破冰船在規(guī)則波中的波浪增阻，分析了附加阻尼對(duì)艏斜浪波浪增阻的影響，得出以下結(jié)論：

1）三維非線性勢(shì)流方法求解波浪增阻問題計(jì)算效率較高，高效準(zhǔn)確地獲得了極地破冰船不同浪向下波浪增阻的變化規(guī)律，以迎浪下的波浪增阻最嚴(yán)重，隨著浪向的偏移，波長較長區(qū)域的波浪增阻逐漸下降。

2）基于固定模的方式獲得了極地破冰船迎浪中波浪增阻的成分，繞射增阻隨波長的變化較為穩(wěn)定，輻射增阻隨波長的變化為單峰形式，峰值對(duì)應(yīng)的波長比和總的波浪增阻峰值對(duì)應(yīng)的波長比相同。

3）通過研究附加阻尼對(duì)波浪增阻的影響發(fā)現(xiàn)附加阻尼可以有效抑制橫搖運(yùn)動(dòng)響應(yīng)，并降低了部分波長區(qū)間下的波浪增阻，改善了阻力時(shí)歷曲線的非線性。

參考文獻(xiàn)

[1] Larsson L， Stern F， Visonneau M. Numerical ship hydrodynamics： An assessment of the Gothenburg 2010 workshop [M]. Gewerbestrasse： Springer Nature Switzerland AG， 2013.

[2] Hino T， Stern F， Larsson L， et al. Numerical Ship Hydrodynamics： An Assessment of the Tokyo 2015 Workshop[M]. Gewerbestrasse： Springer Nature Switzerland AG， 2020.

[3] Sadat-Hosseini H， Wu P C， Carrica P M， et al. CFD verification and validation of added resistance and motions of KVLCC2 with fixed and free surge in short and long head waves[J]. Ocean Engineering， 2013， 59： 240-273.

[4] Joncquez S A G. Second-order forces and moments acting on ships in waves[D]. Copenhagen： Technical University of Denmark， 2009.

[5] S?ding H， Shigunov V， Schellin T E， et al. A Rankine panel method for added resistance of ships in waves[J]. Journal of Offshore Mechanics and Arctic Engineering， 2014， 136（3）： 031601.

[6] Hong L， Zhu R， Miao G， et al. An investigation into added resistance of vessels advancing in waves[J]. Ocean Engineering， 2016， 123： 238-248.

[7]洪亮， 朱仁傳， 繆國平， 等. 基于三維輻射能量法的船舶波浪增阻計(jì)算分析[J]. 船舶力學(xué)， 2018， 22（7）： 807-817.

[8] Valanto P， Hong Y P. Experimental investigation on ship wave added resistance in regular head， oblique， beam， and following waves[C]. Proceedings of the 25th International Ocean and Polar Engineering Conference， Hawaii， 2015.

[9] Sprenger F， Maron A， Delefortrie G， et al. Experimental studies on seakeeping and maneuverability of ships in adverse weather conditions[J]. Journal of Ship Research， 2017， 61（3）： 131-152.

[10] Liu S， Papanikolaou A. Prediction of the added resistance of ships in oblique seas[C]. Proceedings of the 26th International Ocean and Polar Engineering Conference， Rhodes， 2016.

[11] Zhan J H， Kuang X F. Numerical simulation of added resistance in heading and oblique waves using OpenFOAM[C]. Proceedings of the 13th OpenFOAM Workshop， Shanghai， 2018.

[12] Graf K， Pelz M， Bertram V， et al. Added resistance in seaways and its impact on yacht performance[C]. The 18th Chesapeake Sailing Yacht Symposium， Annapolis， 2007.

[13] Moctar O E， Shigunov V， Zorn T. Duisburg Test Case： Post-Panamax Container Ship for Benchmarking[J]. Ship Technology Research， 2012， 59（3）： 50-64.

[14] Zakaria N M G， Baree M S. Alternative methods on added resistance of ships in regular head waves[J]. The Institution of Engineers， Malaysia， 2007， 68（02）：15-22.