冷卻模式對(duì)NM400相變塑性及殘余應(yīng)力的影響

方玉　丁文紅　魯小軒 梁亮　汪凈 彭沖

關(guān)鍵詞：冷卻模式；耐磨鋼；連續(xù)冷卻；殘余應(yīng)力；相變塑性

0 前言

針對(duì)某廠熱軋帶鋼連續(xù)冷卻過(guò)程中采取的2種冷卻模式（一種是全程快冷，一種是前置式超快速冷卻+空冷）而造成的板形差異問(wèn)題，本文以耐磨鋼NM400為研究對(duì)象，通過(guò)熱模擬試驗(yàn)、基于斷裂力學(xué)原理的裂紋柔度法以及建立ABAQUS有限元仿真模型，弄清了NM400在連續(xù)冷卻過(guò)程的相變行為以及冷卻速度對(duì)其相變行為的影響規(guī)律，為改善NM400連續(xù)冷卻過(guò)程殘余應(yīng)力水平及分布、減少板形缺陷提供了數(shù)據(jù)基礎(chǔ)和理論依據(jù)。

1 試驗(yàn)材料及方法

1.1 試驗(yàn)材料

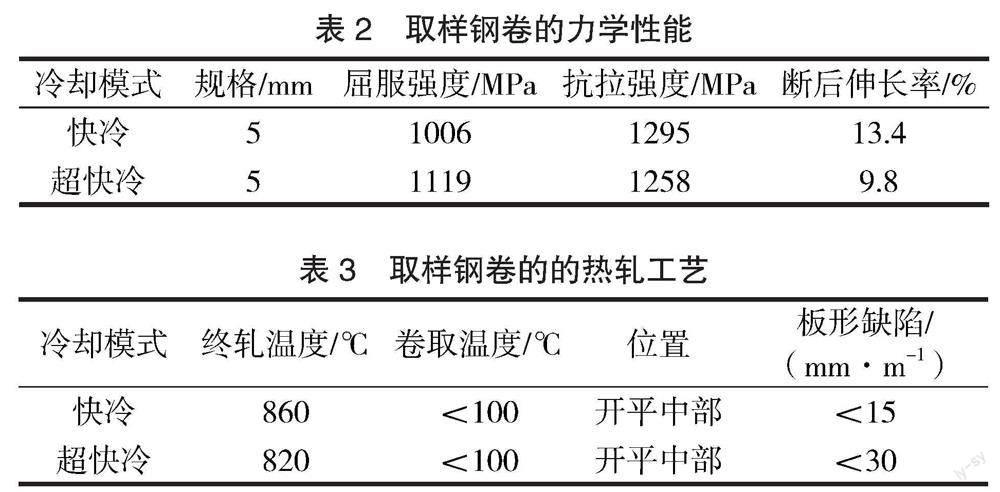
試驗(yàn)材料來(lái)自國(guó)內(nèi)某廠生產(chǎn)的耐磨鋼NM400，厚度為5 mm，寬度為1 500 mm，其化學(xué)成分、力學(xué)性能及軋制工藝參數(shù)分別見表1～表3。NM400在軋后冷卻過(guò)程中采取了2種冷卻模式：快冷和超快冷。快冷是通過(guò)控制冷卻水閥門的開啟密度，減少帶鋼表面積水，從而改善帶鋼的不均勻冷卻。超快冷與傳統(tǒng)的冷卻工藝相比，冷卻速度可達(dá)到常規(guī)冷卻的2～5倍。本文涉及到的超快冷為前置式（前置式超快冷設(shè)備安裝在層流冷卻設(shè)備之前）。

1.2 試驗(yàn)方法

1.2.1 殘余應(yīng)力測(cè)試

從現(xiàn)場(chǎng)2種熱軋工藝的鋼卷上，沿帶鋼寬度方向從操作側(cè)開始以帶鋼寬度1/2為對(duì)稱中心，各取9個(gè)測(cè)試點(diǎn)作為殘余應(yīng)力測(cè)試樣，共18塊測(cè)試樣（100 mm×90 mm）。通過(guò)前期課題組開發(fā)的裂紋柔度法實(shí)測(cè)2種冷卻模式下的殘余應(yīng)力，裂紋柔度法的測(cè)量原理是在被測(cè)物體的表面引入一條深度逐漸增加的裂紋來(lái)釋放殘余應(yīng)力，通過(guò)測(cè)量特定點(diǎn)的應(yīng)變值來(lái)計(jì)算殘余應(yīng)力。

1.2.2 連續(xù)冷卻過(guò)程的相變動(dòng)力學(xué)及相變塑性試驗(yàn)

從其他厚度規(guī)格的成品鋼板上沿軋制方向取中部材料，加工成直徑為?6 mm×10 mm的試樣。將試樣裝入Gleeble3500熱模擬試驗(yàn)機(jī)后抽真空，并充入氬氣以減少氧化。隨后以100℃/s的升溫速率將試樣加熱至1 000℃，保溫5 min。然后以1℃/s的冷卻速度將試樣冷卻至950℃，并在該溫度下保溫10 s，進(jìn)行第一道次壓縮變形，變形量ε=30%，變形速率ε為1s-1；首道次壓縮完成后，以1℃/s的冷卻速度將試樣冷卻至860℃，保溫10s，同時(shí)進(jìn)行第二道次壓縮變形，變形量ε=30%，變形速率ε為1s-1，雙道次壓縮完成后，再分別以20、30、40、45℃/s的冷卻速度將試樣冷卻至室溫；第二道次壓縮完成后，再分別以20、30、40、45℃/s的冷卻速度將試樣冷卻至480℃（相變點(diǎn)以上50℃），對(duì)試樣進(jìn)行快速加載（1 s內(nèi)完成加載），加載載荷分別為：-45、-60、-80MPa，保持上述載荷，并以加載前冷速冷卻至室溫。

1.2.3 ABAQUS子程序開發(fā)

根據(jù)模擬過(guò)程中的溫度和NM400的相變動(dòng)力學(xué)方程，使用USDFLD用戶子程序計(jì)算馬氏體的轉(zhuǎn)變量及增量，將其作為狀態(tài)變量存儲(chǔ)在STATEV中，并傳遞給其他用戶子程序HETVAL和UEXPAN。隨后根據(jù)相變潛熱計(jì)算公式，將馬氏體相變產(chǎn)生的相變潛熱作為內(nèi)生熱源，寫入HETVAL子程序。通過(guò)以上步驟，可以計(jì)算出冷卻過(guò)程中某一點(diǎn)的溫度。最后，使用先前計(jì)算的溫度作為預(yù)定義場(chǎng)，并輸入與熱相關(guān)的力學(xué)參數(shù)，通過(guò)編輯子程序UEXPAN計(jì)算熱應(yīng)變、相變應(yīng)變與相變塑性應(yīng)變，通過(guò)編寫子程序UHARD考慮屈服強(qiáng)度的影響，得到最終的殘余應(yīng)力場(chǎng)。

2 結(jié)果與分析

2.1 試驗(yàn)結(jié)果與分析

2.1.1 裂紋柔度法測(cè)試結(jié)果

由2種冷卻模式下各測(cè)點(diǎn)軋向殘余應(yīng)力沿厚度方向上的分布及應(yīng)力偏差。可知，快冷時(shí)，靠近操作側(cè)的A、B、C、D、E測(cè)點(diǎn)沿厚度方向上的軋向殘余應(yīng)力呈現(xiàn)大“U”形對(duì)稱分布，靠近傳動(dòng)側(cè)的F、G、H、I測(cè)點(diǎn)則呈現(xiàn)“W”形對(duì)稱分布；而超快冷時(shí)各測(cè)點(diǎn)沿厚度方向上的軋向殘余應(yīng)力呈現(xiàn)“N”形不對(duì)稱分布，超快冷時(shí)應(yīng)力水平高。2種冷卻模式下大部分測(cè)點(diǎn)軋向殘余應(yīng)力的偏差均小于該測(cè)點(diǎn)軋向殘余應(yīng)力絕對(duì)值的8%。超快冷時(shí)，A～I(xiàn)測(cè)點(diǎn)的下表面殘余應(yīng)力分別為58.85、36.53、39.30、20.59、30.90、30.39、55.12、-114.36、110.72 MPa，上表面的應(yīng)力分別為-294.38、-7.55、10.68、-172.01、-81.39、-66.26、-59.61、-108.93、-110.66 MPa。大部分測(cè)點(diǎn)上下表面應(yīng)力狀態(tài)為：一個(gè)受拉應(yīng)力，一個(gè)受壓應(yīng)力，說(shuō)明此時(shí)帶鋼上下表面延伸不一致，更容易在后續(xù)加工過(guò)程中產(chǎn)生由于上下表面應(yīng)力非對(duì)稱分布所導(dǎo)致的加工畸變。

2.1.2 冷卻速度對(duì)NM400相變動(dòng)力學(xué)的影響

熱模擬相變動(dòng)力學(xué)試驗(yàn)中，由不同冷卻速度下NM400的組織。可知，當(dāng)冷卻速度為20℃/s時(shí)，組織中存在少量貝氏體，大部分為馬氏體；當(dāng)冷卻速度在30℃/s以上時(shí)，全部為馬氏體組織。

為了了解NM400連續(xù)冷卻過(guò)程殘余應(yīng)力演變規(guī)律，掌握NM400轉(zhuǎn)變進(jìn)程至關(guān)重要。通過(guò)杠桿法以及修正后的K-M方程擬合可得到不同冷卻速度下的相變動(dòng)力學(xué)曲線和相變動(dòng)力學(xué)方程。修正后的K-M方程見式（1）。

δ=1-exp[-α（Ms-t）n]（1）

式中：δ為馬氏體轉(zhuǎn)變量；α為相變動(dòng)力學(xué)系數(shù)；Ms為馬氏體相變開始溫度；t為冷卻過(guò)程中的溫度；n為修正系數(shù)。

20℃/s：δ=1-exp[-0.02003×（393.34-t）1.1]（2）

30℃/s：δ=1-exp[-0.02740×（370.83-t）1.1]（3）

40℃/s：δ=1-exp[-0.02430×（363.22-t）1.1] （4）

45℃/s：δ=1-exp[-0.02993×（389.89-t）1.1] （5）

式（2）～式（5）為不同冷卻速度下的相變動(dòng)力學(xué)方程。

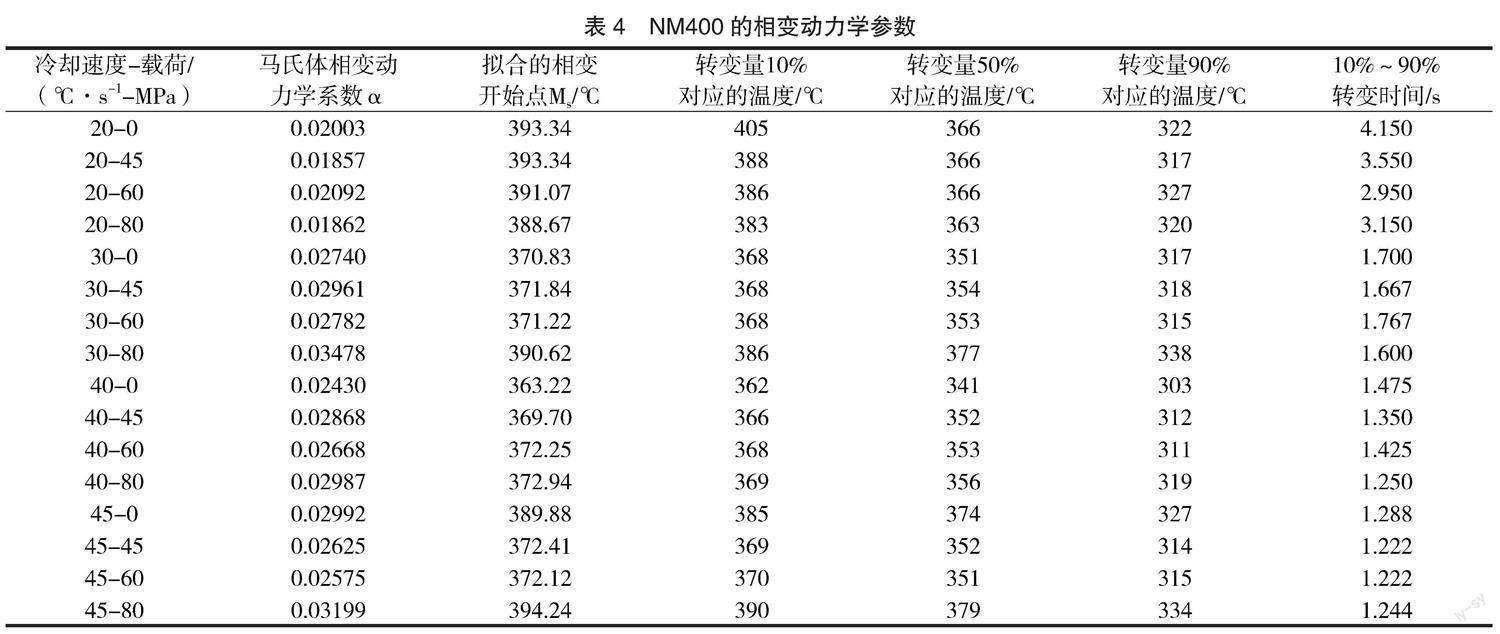
由不同冷卻速度（20、30、40、45℃/s）下的馬氏體相變開始溫度分別為393.34、370.83、363.22和389.89℃，在冷卻速度為20～40℃/s時(shí)，隨著冷卻速度的增加，相變開始點(diǎn)與結(jié)束點(diǎn)均降低；當(dāng)冷速為45℃/s時(shí)，NM400的相變開始溫度升高至389.89℃。不同冷卻速度（20、30、40、45℃/s）下，馬氏體轉(zhuǎn)變10%～90%時(shí)間分別為4.150、1.700、1.475和1.288s，并且馬氏體轉(zhuǎn)變10%～50%所需的時(shí)間均小于馬氏體轉(zhuǎn)變50%～90%，即冷速增加，相變時(shí)間縮短，且馬氏體前期轉(zhuǎn)變遠(yuǎn)快于后期。在相變轉(zhuǎn)變量小于80%時(shí)，NM400的相變速率近似恒定；當(dāng)材料的轉(zhuǎn)變量大于80%后，材料的相變速率明顯降低。而且，冷卻速度越大，相變后期相變速率降低的現(xiàn)象越顯著。

2.1.3 應(yīng)力對(duì)NM400相變動(dòng)力學(xué)的影響

從表4可知，外加載荷對(duì)NM400相變動(dòng)力學(xué)的影響相對(duì)較小，而冷卻速度對(duì)NM400相變動(dòng)力學(xué)的影響較為顯著，且隨著冷卻速度的增加，NM400的相變時(shí)間近似呈線性減小。據(jù)此，可將相變動(dòng)力學(xué)系數(shù)修正為式（6）。

α=0.0003v+0.01529（6）

式中：v為冷卻速度。

隨著冷卻速度的增加，Ms點(diǎn)呈先下降、再上升的趨勢(shì)，冷卻速度為40℃/s時(shí)，Ms點(diǎn)達(dá)到極小值363.22℃。載荷對(duì)Ms點(diǎn)的影響未呈現(xiàn)出一致性規(guī)律，在本次計(jì)算中僅考慮冷速對(duì)相變開始點(diǎn)的影響，并表達(dá)為式（7）。

Ms=-0.75v+398（7）

從而得到考慮冷卻速度影響的相變動(dòng)力學(xué)方程式（8）。

δ=1-exp[-（0.003v+0.01529）×（-0.75v+398-t）1.1]（8）

2.1.4 NM400相變塑性研究

在較小的應(yīng)力作用下會(huì)發(fā)生明顯的相變塑性變形，壓應(yīng)力作用下產(chǎn)生的相變塑性應(yīng)變均為負(fù)值，相變塑性應(yīng)變與應(yīng)力加載方向具有一致性。

根據(jù)Greenwood-John模型相變塑性一般可表示為

εtp=kσδ（9）

式中：k為相變塑性系數(shù)；σ為外加應(yīng)力。

當(dāng)馬氏體相變結(jié)束后，即馬氏體體積分?jǐn)?shù)為1時(shí)，式（9）可以簡(jiǎn)化為式（10）。

εtp=kσ（10）

通過(guò)式（10）得到各個(gè)冷卻速度（20、30、40、45℃/s）下的相變塑性系數(shù)k分別為8.9119×10-5、9.7734×10-5、9.1414×10-5和8.3259×10-5，隨著冷卻速度的增加，相變塑性系數(shù)先增大后減小。冷卻速度在20℃/s時(shí)，存在少量的貝氏體組織，對(duì)馬氏體相變塑性的計(jì)算過(guò)程中存在一定的影響，通過(guò)對(duì)冷卻速度30℃/s以上的相變塑性系數(shù)k進(jìn)行擬合，得到方程見式（10）。

k=1.2597×10-4-9.1740×10-7v（11）

在試驗(yàn)參數(shù)范圍內(nèi)，相變塑性應(yīng)變隨著加載應(yīng)力的增加而近似線性增大；而冷卻速度對(duì)相變塑性應(yīng)變的影響相對(duì)較小。

2.2 模擬結(jié)果與分析

2.2.1 相變塑性對(duì)殘余應(yīng)力的影響

本文以5 mm×1 500 mm規(guī)格的NM400為例，通過(guò)修改UEXPAN子程序，將相變塑性應(yīng)變當(dāng)做一獨(dú)立應(yīng)變加入至本構(gòu)方程中實(shí)現(xiàn)數(shù)值模擬，得到了相變塑性對(duì)殘余應(yīng)力的影響規(guī)律。

通過(guò)ABAQUS提取帶鋼表面與心部的應(yīng)力數(shù)據(jù)可知第Ⅰ階段：溫度場(chǎng)驅(qū)動(dòng)下的應(yīng)力分布。NM400剛開始冷卻時(shí)，表面受拉應(yīng)力，心部受壓應(yīng)力，該應(yīng)力影響初始相變塑性應(yīng)變方向。

第Ⅱ階段：表面相變驅(qū)動(dòng)下的應(yīng)力分布。當(dāng)帶鋼NM400表面到達(dá)相變溫度，開始相變。在相變應(yīng)變影響下，帶鋼表面相變區(qū)域體積膨脹，隨著相變轉(zhuǎn)變量的增加，表面拉應(yīng)力迅速切換為壓應(yīng)力，并帶動(dòng)心部應(yīng)力由壓應(yīng)力切換為拉應(yīng)力。由于相變塑性應(yīng)變的方向與應(yīng)力偏張量方向一致，因此，相變塑性應(yīng)變也由初始的拉應(yīng)變迅速切換為壓應(yīng)變。此時(shí)，相變塑性應(yīng)變抵消部分相變膨脹應(yīng)變的影響，抑制了殘余應(yīng)力的增長(zhǎng)。所以，在這一階段，考慮相變塑性應(yīng)變時(shí)的應(yīng)力顯著低于不考慮相變塑性應(yīng)變時(shí)的應(yīng)力。

第Ⅲ階段：心部相變驅(qū)動(dòng)下的應(yīng)力分布。當(dāng)帶鋼NM400心部到達(dá)相變溫度后，開始相變。在帶鋼心部相變應(yīng)變的影響下，心部相變區(qū)域體積膨脹，使得由表面相變所導(dǎo)致的拉應(yīng)力逐步減少。受應(yīng)力的偏張量影響，此時(shí)帶鋼心部的相變塑性應(yīng)變?yōu)槔瓚?yīng)變，與相變應(yīng)變的方向一致，因此，相變塑性應(yīng)變與相變應(yīng)變疊加，使心部應(yīng)力迅速由拉應(yīng)力切換為壓應(yīng)力，并帶動(dòng)表面應(yīng)力由壓應(yīng)力切換為拉應(yīng)力。當(dāng)不考慮相變塑性應(yīng)變時(shí)，應(yīng)力變化的驅(qū)動(dòng)力僅有相變應(yīng)變，因此，不考慮相變塑性應(yīng)變時(shí)，NM400殘余應(yīng)力的計(jì)算結(jié)果要小于實(shí)際值。

第Ⅲ階段后的平穩(wěn)階段是心部相變結(jié)束后，帶鋼表面與心部應(yīng)力趨于穩(wěn)定。因此，相變塑性應(yīng)變對(duì)殘余應(yīng)力的影響取決于相變時(shí)刻應(yīng)力偏張量的方向及大小（相變塑性應(yīng)變的大小與正負(fù)），直接影響著相變后帶鋼內(nèi)的殘余應(yīng)力分布。

2.2.2 連續(xù)冷卻過(guò)程殘余應(yīng)力的形成機(jī)制

本文重點(diǎn)討論軋后的連續(xù)冷卻過(guò)程，通過(guò)計(jì)算連續(xù)冷卻過(guò)程的溫度場(chǎng)、應(yīng)變場(chǎng)和應(yīng)力場(chǎng)探討冷卻模式對(duì)NM400殘余應(yīng)力影響的內(nèi)在機(jī)制。

（1）溫度場(chǎng)對(duì)比分析。

由不同冷卻模式下的溫度和溫度差變化可知，快冷時(shí)，帶鋼厚度方向上的最大溫差為28℃，而超快冷時(shí)，帶鋼厚度方向上的溫差高達(dá)189℃，這意味著超快冷模式下，溫度應(yīng)力對(duì)相變行為的影響更為顯著。

（2）應(yīng)變對(duì)比分析。

由于在超快冷模式下帶鋼表面與心部溫差大，且超快冷速下NM400的相變速率大，因此當(dāng)帶鋼心部開始相變時(shí)，表面相變已經(jīng)完成94%。而在快冷模式下，當(dāng)帶鋼心部開始相變時(shí)，表面相變僅完成35%。導(dǎo)致超快冷模式下，帶鋼心部相變所產(chǎn)生的相變塑性應(yīng)變遠(yuǎn)大于快冷模式下帶鋼心部相變所產(chǎn)生的相變塑性應(yīng)變。

（3）殘余應(yīng)力對(duì)比分析。

導(dǎo)致超快冷模式下帶鋼應(yīng)力水平高的主要原因是：帶鋼心部相變前，表面帶鋼相變體積分?jǐn)?shù)過(guò)大，造成帶鋼心部相變時(shí)所受的拉應(yīng)力過(guò)大，誘導(dǎo)心部帶鋼產(chǎn)生與相變應(yīng)變同向的大相變塑性應(yīng)變，因而在帶鋼內(nèi)部造成高幅值的殘余應(yīng)力。

2.3 實(shí)測(cè)與模擬對(duì)比

本文建立的NM400殘余應(yīng)力預(yù)測(cè)模型，考慮了冷卻速度對(duì)相變動(dòng)力學(xué)及相變塑性的影響，以E測(cè)點(diǎn)為例，模擬與實(shí)測(cè)對(duì)比結(jié)果見表5。模擬與裂紋柔度法的實(shí)測(cè)結(jié)果數(shù)值存在差異，但均超快冷時(shí)應(yīng)力水平較高。其主要原因如下：（1）裂紋柔度法的實(shí)測(cè)試樣為開平加工后的，開平加工改變了帶鋼內(nèi)部的殘余應(yīng)力分布規(guī)律，因此，模擬計(jì)算值必然與實(shí)測(cè)數(shù)據(jù)存在差異；（2）本文模擬的連續(xù)冷卻過(guò)程是理想情況下的，未考慮卷取張力以及板形缺陷釋放對(duì)殘余應(yīng)力的影響。

3 結(jié)論

（1）實(shí)測(cè)與模擬結(jié)果均表明，超快冷時(shí)應(yīng)力水平較高。導(dǎo)致超快冷后帶鋼殘余應(yīng)力水平高的關(guān)鍵原因是：加大冷速后提高了帶鋼心部相變開始時(shí)帶鋼表面相變的體積分?jǐn)?shù)。該體積分?jǐn)?shù)越大，心部開始相變時(shí)所受到的拉應(yīng)力水平越高，相變所產(chǎn)生的相變塑性應(yīng)變?cè)酱蟆Ｓ捎诖藭r(shí)所形成的相變塑性應(yīng)變與相變應(yīng)變同向，兩者疊加后在材料內(nèi)引入高幅殘余應(yīng)力。

（2）連續(xù)冷卻過(guò)程殘余應(yīng)力的形成包括3個(gè)階段，分別為熱應(yīng)力主導(dǎo)階段、表面相變主導(dǎo)階段和心部相變主導(dǎo)階段。3個(gè)階段之間通過(guò)前一階段的應(yīng)力對(duì)后一階段相變塑性應(yīng)變的影響而相互關(guān)聯(lián)，帶鋼內(nèi)最終的殘余應(yīng)力由心部相變所產(chǎn)生塑性應(yīng)變所決定。

（3）相變塑性應(yīng)變的大小及方向與加載在相變瞬間的應(yīng)力直接相關(guān)。對(duì)于NM400而言，在帶鋼表面相變階段，相變塑性應(yīng)變與相變應(yīng)變方向相反，抑制表面相變階段殘余應(yīng)力的增長(zhǎng)；在帶鋼心部相變階段，相變塑性應(yīng)變與相變應(yīng)變方向相同，促進(jìn)心部相變階段殘余應(yīng)力的增長(zhǎng)。

本文摘自《鋼鐵》2023年第4期