數學通訊第531號問題的另解

陸信明　周娜

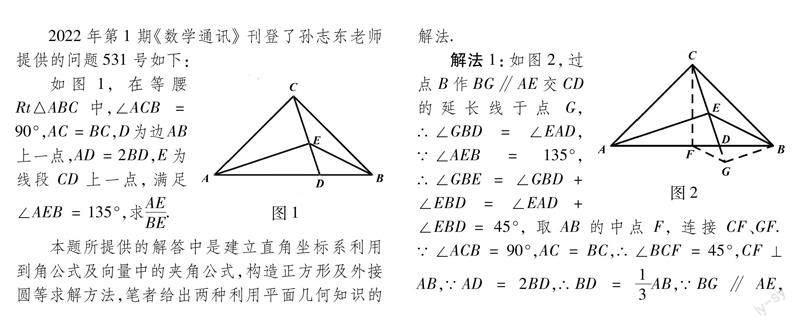
2022年第1期《數學通訊》刊登了孫志東老師提供的問題531號如下：

如圖1，在等腰Rt△ABC中，∠ACB=90°，AC=BC，D為邊AB上一點，AD=2BD，E為線段CD上一點，滿足∠AEB=135°，求AE/BE．

本題所提供的解答中是建立直角坐標系利用到角公式及向量中的夾角公式，構造正方形及外接圓等求解方法，筆者給出兩種利用平面幾何知識的解法．

由上述二解可見，本題解答的難點在于∠AEB=135°這一條件的運用，通過觀測不難猜得∠AED=90°，∠BED=45°，這為解決問題提供了方向．解法1從AD=2BD入手，構造相似三角形，通過將已知中135°角轉移，構造B、G、F、C四點共圓，得出∠AED=90°，從而解決了問題．解法2也是從AD=2BD入手，構造相似三角形、等腰直角三角形，由全等三角形，得出∠BEF=45°，最終也實現問題的解決．

參考文獻

［1］陸信明．數學通報2596號問題的另證與推廣［J］．中學數學教學，2021（1）：57．