艦船地震波遠程定位方法研究

薛澤利，張曉峻,侯金弟，孫晶華

(1.佳木斯大學 理學院，黑龍江 佳木斯 154007；2.哈爾濱工程大學 物理與光電工程學院，黑龍江 哈爾濱 150001)

隨著艦船制造技術的提高，水聲高頻信號被進一步抑制，傳統水聽器由于尺寸、設計原理等原因很難準確有效檢測低頻信號[1]. 同時淺海海域的地形復雜，渾濁海水對聲波的吸收，不利于水聲的遠程傳播[2]，因此利用水聲遠程定位艦船目標變得越來越困難. 在淺海海域艦船水聲傳播至海底沉積層表面形成了足夠能量的艦船地震波，可以遠程傳播[3]，因此利用艦船地震波遠程定位，可以彌補水聲遠程定位的不足.

艦船地震波是水聲在海底沉積層表面形成的橢圓波，艦船地震波能量主要集中在固體-液體分界表面[4]，沿著固體-液體分界面上衰減緩慢，可以遠程傳播. 海底地震計組成的九元環形陣列具有波數響應靈敏度高、各方向響應均勻等優點. 基于此陣列，側向定位和時差法無法準確定艦船目標，采用梯度下降算法和單純形算法可以減小定位誤差，實現穩定精確定位艦船目標.

1 艦船地震波耦合與傳輸

水聲是一種縱波，當淤泥層的水聲傳播至沉積層表面與海底沉積層發生作用，使得沉積層發生應變. 其中切應變產生水平方向的振動變成縱波，正應變產生豎直方向的振動變成橫波，所以縱波在沉積層表面作用點處發生波形轉換. 水聲在分界面處波形轉換如圖1所示，其中P波為縱波，S波為橫波.

圖1 水聲在沉積層表面的波形轉換

在沉積層作用點處，產生的S波又可以分解為振動方向垂直于分界面的SV波和平行于分界面的SH波[5]，艦船地震波是P波和SV波在淤泥層和沉積層分界表面合成的一種振動軌跡為沿著逆時針旋轉的橢圓波，在圖2所示的坐標系中，波的水平傳播方向為x軸，垂直傳播方向為z軸.

圖2 艦船地震波位移

艦船地震波振動的位移分解為水平方向u和豎直方向w的位移[6]可以表示為

(1)

(2)

式(1)和式(2)中,λST為艦船地震波波長，vST為艦船地震波波速，ω為艦船地震波角速度，在式(2)和式(3)中的其他函數為

(3)

(4)

(5)

(6)

(7)

vP為縱波波速，vS為橫波波速，艦船地震波滿足于橢圓軌跡方程,

(8)

(9)

(10)

2 定位陣列

利用三維高靈敏度海底地震計可以檢測艦船地震波[9]，但是利用單一海底地震計并不能實現對目標的定位，需要多個海底地震計組成的陣列才能實現對目標的定位. 如圖3所示，建立九元海底地震計環形陣列，其中M0～M8表示海底地震計的位置，M0位于原點處，其他陣元M1～M8均勻地分布在圓周上，R為九元海底地震計環形陣列的半徑.

圖3 九元環形陣

陣列的波數響應是陣列的重要指標，陣列的波數響應主瓣大而尖，并且邊瓣小，表征陣列可以壓制潛在的干擾信號，從而保證定位的精度. 陣列的波數響應[10]可以表示為

(11)

式中，N是海底地震計的數目，rj和rs表示海底地震計的位置矢量，九元海底地震計環形陣列半徑R為1 km，波數響應圖如圖4所示，其中y(k)表示y方向的波數，x(k)表示x方向的波數，H(k)表示波數振幅響應.

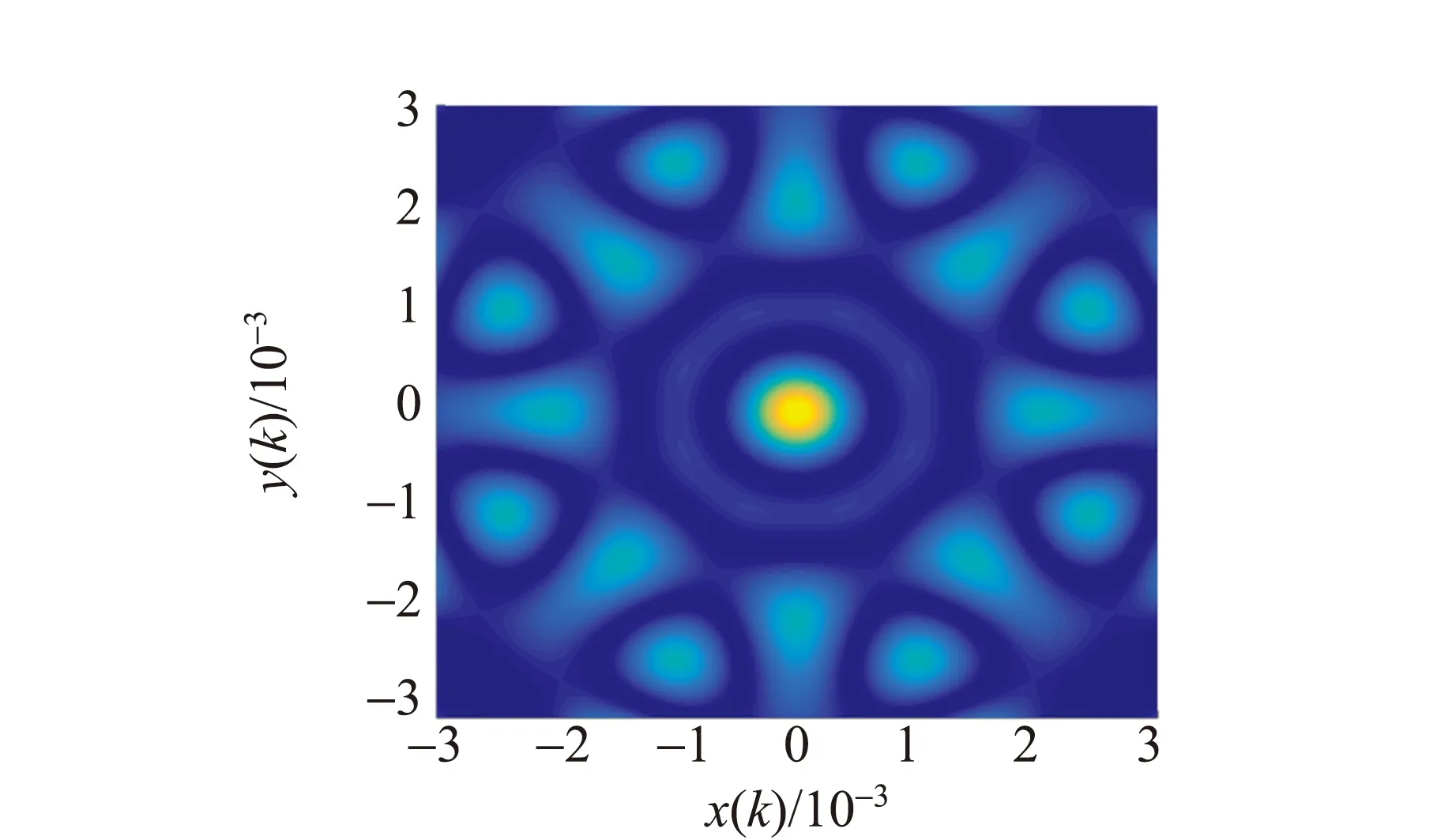
(a)二維波數響應

(b)三維波數響應圖4 九元圓形海底地震計陣列的波數響應

圖4(a)中二維波數響應圖表明，環形陣對每個方向的波數響應一致，也就是對每個方向的定位精度一致. 圖4(b)中三維波數響應圖表明，九元海底地震計環形陣列的波數響應主瓣高邊瓣小，波數分辨率高，可以壓制潛在的干擾信號，保證陣列定位的精度.

3 定位算法

利用海底地震計組成的陣列對艦船目標進行定位，最常用的定位方法是測向法定位和時差法定位[11]，但是利用測向法定位需要海底地震計能夠準確地檢測到艦船地震波的波達角. 當艦船目標在較遠的位置移動時，艦船地震波的波達角變化很小，海底地震計難以準確檢測到艦船地震波的方向. 時差法是利用海底地震計陣列檢測艦船地震波到達不同海底地震計所形成的時間實現對目標的定位[12]. 時差法在求解目標位置時，通常不能得到唯一解，所以時差法通常不能得到目標的唯一坐標位置[13]. 針對側向法和時差法的不足，采用梯度下降算法和單純形算法對目標進行定位研究.

3.1 梯度下降算法

梯度下降算法是基于泰勒級數展開的算法[14]. 利用梯度下降算法對艦船目標定位，其運算的流程如圖5所示，首先在二維坐標平面選取初始的點x0，計算初始點函數值，如果函數值f(x0)滿足停止條件，停止運算輸出結果x0，否則按照一定規則變換到下一個xk+1點繼續運算，直到滿足停止條件ε0，停止運算輸出結果.

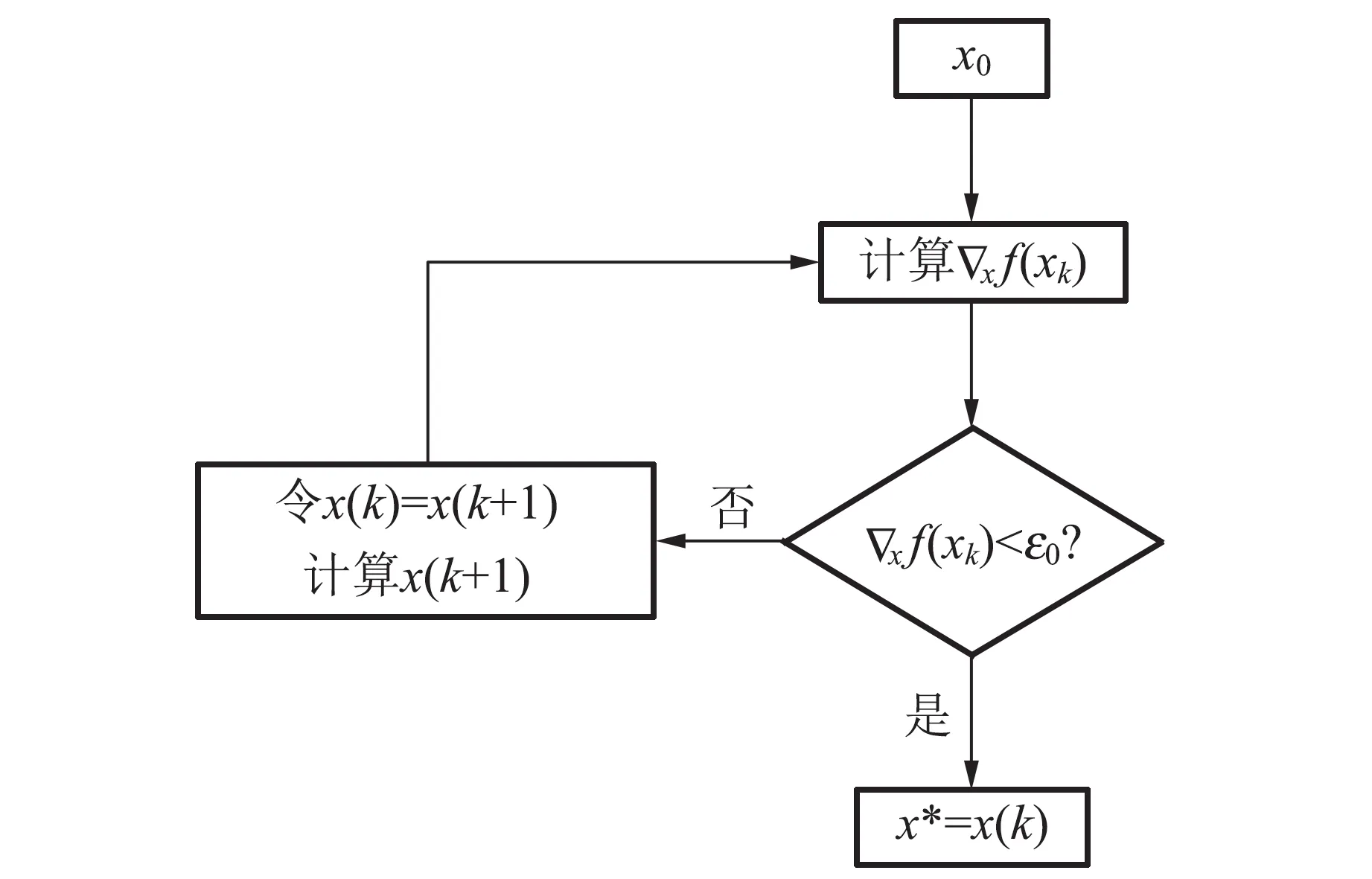
圖5 梯度下降算法運算流程

依據時差法的定位原理，誤差矢量可以表示為[15-16]

e(x)=Ax-(M-vSTτi‖x‖),

(12)

代價函數可以表示為

f(x)=eTe,

(13)

代價函數的梯度可以表示為

(14)

由第k個點變換到第k+1個點的變換準則為

x(k+1)=x(k)-μxf(xk),

(15)

其中中μ為下降速度.

3.2 單純形算法

利用單純形算法陣列定位的殘差[17]可以表示為

(16)

式(16)中n為方程數，對于九元海底地震計環形陣列的方程數為8，對于二維平面定位q為3.ti為艦船地震波到達第i個傳感器的時間，tm表示ti的中位數，在九元環形陣中tm=t0.

(17)

f(x)=E(x).

(18)

二維空間內的單純形算法首先在二維空間定義3個任意點，分別為x1,x2和x3，3個點相互連接構成了“單純形”. 定義一個函數為f(xi)，這個函數是誤差函數，在這個二維空間的單純性的各個頂點的函數值定義為

fi=f(xi),i=1,2,3.

(19)

在這個單純形中，頂點的最大值和最小值分別定義為

fm=maxf(xi),

(20)

fn=minf(xi).

(21)

最大值頂點定義為xm，最小值頂點為xn，大于最小值且小于最大值的點定義為xg，單純形的形心點[18]的坐標為

(22)

(23)

(24)

在式(24)中擴展系數V>1，形成新的單純形，直到滿足條件輸出結果.

(25)

(26)

(27)

單純形法算法運算流程圖如圖6所示[19].

圖6 單純形算法流程圖

這種變化是把單純形的邊縮短了，緊縮系數為L=0.5，其中xi≠xm，形成新的單純形繼續循環，直到f(x*)的值滿足設定的條件時停止運算. 單純形算法每1次循環都是通過映射、擴展、壓縮、縮短邊長中的某一種方式變換得到新的單純形[20]. 當單純形的最大值滿足設定的條件f(xm)<ε0時，停止運算輸出xm，運算結束.

4 仿真計算

圖7 九元海底地震計環形陣定位模型

利用梯度下降算法進行定位時首先選擇初始點，通過初始點的變換，最終變換到估計的位置，研究初始點對定位的影響，選擇3種不同初始點進行定位，初始點a的坐標位置為(2，2.5)，初始點b的坐標位置為(35，75)，初始點c的坐標位置為(40，25).

梯度下降算法3種不同的初始點定位的結果如表1所示，其中μ是下降速度設置為0.01，下降速度是進行運算時變換的步長，ε0是停止條件設置為0.001，當代價函數的梯度小于停止條件ε0時停止運算，輸出估計的目標的位置S*. 其中利用a初始點最終估計的位置為(32.405，75.421)，其中利用b初始點最終估計的位置為(45.692，79.051)，其中利用c初始點最終估計的位置為(44.950，80.523).

表1 梯度下降算法定位結果

研究初始單純形對定位的影響，首先選擇3種不同的初始單純形進行定位，a初始單純形的3個初始點分別為x1(1，2.5),x2(10，8.7),x3(6，50)，b初始單純形的3個初始點分別為x1(30，45),x2(50，115),x3(65，50)，c初始單純形的3個初始點分別為x1(50，10),x2(35，25),x3(65，40).

3種不同初始單純形算法的定位結果如表2所示，其中T是映射系數設置為1，V是擴展系數設置為1.2，Z是壓縮系數設置0.5，L是緊縮系數設置為0.5，ε0是停止條件設置為0.001，當陣列的殘差小于停止條件時輸出估計的目標的位置S*，最終a初始單純形最大值點變換到(46.462，80.454)停止運算輸出結果S*(46.462，80.454)，最終b初始單純形最大值點變換到(46.418，80.351)停止運算輸出結果S*(46.418，80.351)，c初始單純形最大值點變換到(46.421，80.349)停止運算輸出結果S*(46.421，80.349).

表2 單純形算法定位結果

采用定位誤差和對初始值的依賴程度對梯度下降算法和單純形算法定位效果進行評價. 目標的定位誤差是指算法估計的位置與實際位置的空間距離，定位誤差可以表示為

(28)

(29)

在式(29)中，n表示定位的次數為3.

2種算法的定位誤差和對初始值的依賴程度如表3所示，單純形算法定位目標的誤差約為0.2 km，對初始值的依賴程度為1.1×10-5km2. 與梯度下降算法相比，定位誤差小，定位精度高，對初始值的依賴程度小，定位更加穩定，所以相比于梯度下降算法單純形算法對目標定位優勢更明顯，更適合對艦船目標定位.

表3 算法定位性能

5 結 論

從理論上分析了艦船地震波形成的機理，固-液分界表面耦合特性及海底遠程傳播的特性，結果表明艦船地震波遠程傳輸衰減小. 基于九元海底地震計環形陣列,研究了梯度下降算法和單純形算法，結果表明：九元海底地震計環形陣列具有波數響應靈敏度高，各方向響應均勻的特點；利用梯度下降算法和單純形算法對目標位置進行估計，可減小定位誤差；單純形算法定位誤差更小，對初始值的依賴程度更小，定位更加穩定. 因此，基于艦船地震波實現遠程目標定位具有可行性.