基于遺傳神經網絡的艦船磁場等效源重構方法

王毅, 周國華, 武曉康, 朱雪蓮

(海軍工程大學 電氣工程學院,湖北 武漢 430033)

對于艦船磁隱身而言,準確預測艦船磁場的空間分布至關重要[1-2]。目前,存在多種預測模型,最常用的是等效源模型,包括磁單極子、旋轉橢球體、磁偶極子、旋轉橢球體與磁偶極子混合模型等。影響等效源模型預測效果的因素很多,重要的是等效磁源的參數設置,包括磁源的數量和位置。張朝陽等[3-4]采用粒子群、模擬退火等算法,對等效磁源的數量和位置進行優(yōu)化設計,獲得了艦船磁場預測模型,該類模型存在計算量大、預測結果不穩(wěn)定的特點。郭成豹等[5]根據艦船的真實鐵磁結構,設計了艦船等效磁源的三維空間分布,并利用Tikhonov正則化反演技術,對磁源數量和位置設置引起的病態(tài)問題進行了求解,實現(xiàn)了艦船磁場的準確預測,這種方法也存在建模復雜、正則化參數設置難等問題。

近年來,隨著機器學習的不斷發(fā)展,以數據挖掘和非線性預測為特征的人工神經網絡被進一步開發(fā),在電磁輻射領域得到廣泛應用[6-8]。溫軍等[9]利用級聯(lián)神經網絡,建立了等效電磁偶極子混合模型,解決了未知電磁干擾源的輻射場預測難題。舒余飛等[10]利用人工神經網絡,實現(xiàn)了復雜電磁環(huán)境下電子產品的等效輻射源的高精度建模。

本文以傳統(tǒng)等效源模型為核心,借助人工神經網絡的非線性預測和遺傳算法的自適應尋優(yōu)功能,提出利用遺傳神經網絡(genetic neural networks,GNN)[11-12]重構艦船磁場等效源的預測方法。通過多次學習訓練,得到包含磁源信息的隱性等效源模型[13]。

1 遺傳神經網絡模型構建

1.1 傳統(tǒng)等效源方法

根據鐵磁性艦船空間分布,設置一定數量的磁偶極子,用這些磁偶極子代替艦船的真實磁源。在艦船坐標系下,磁偶極子坐標記為Qi(ui,vi,wi),空間任意點坐標記為Pj(xj,yj,zj),空間任意點的三分量磁場Bj(Bxj,Byj,Bzj)為:

(1)

式中:mui、mvi、mwi分別表示第i個磁偶極子沿x、y、z軸方向的磁矩分量;axji、ayji、azji、bxji、byji、bzji、cxji,cyji、czji表示空間系數。

將式(1)矩陣表示為:

G×M=B

(2)

式中:B表示艦船磁場矩陣;G表示磁場測量點與模擬體坐標之間的系數矩陣;M表示各模擬體的三分量磁矩組成的磁矩向量。

若已知艦船磁場測量平面,則系數矩陣G已知,把艦船近場磁場矩陣B代入式(2),即可反演得到艦船等效模擬體的磁矩信息M。在此基礎上,根據目標區(qū)域的場點坐標,形成新的系數矩陣G1,由G1×M即可預測目標區(qū)域的磁場信息。

在利用上述方法預測艦船周圍空間磁場時,由于難以獲得磁偶極子的最佳數量和位置分布,式(2)將會變成一個不穩(wěn)定的矩陣方程,求解磁矩向量M的反演過程無法嚴格成立,影響了艦船磁場預測效果。因此,本文提出利用人工神經網絡的學習能力和遺傳算法的自適應優(yōu)化功能對等效源模型進行重構,避免反演求解過程,提高艦船磁場的預測精度。

1.2 遺傳神經網絡

1)人工神經網絡[14-16]。

傳統(tǒng)的等效源方法主要利用艦船磁場B逆推出等效模擬體的磁矩信息M。每個等效模擬體磁矩M的幅值、方向信息已知。本文將系數矩陣G作為人工神經網絡的輸入,艦船磁場B作為人工神經網絡的輸出,通過多次訓練,得到一個隱性的等效源模型。磁矩信息M由人工神經網絡的隱含層節(jié)點數、連接權值、閾值、傳遞函數等參數共同表示。輸入信息(系數矩陣G)根據磁源計算公式推導,與輸出信息(艦船磁場B)之間存在真實的非線性關系,顯著提高神經網絡的訓練效率。

該網絡采用梯度下降法進行訓練,參數更新由神經網絡的反向傳播算法確定。在反向傳播過程中,誤差函數E為:

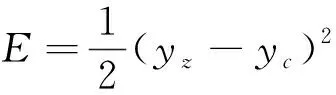
(3)

式中:yz表示訓練集輸出的真實值;yc表示訓練集輸出的預測值。

2)遺傳算法[17-19]。

在利用人工神經網絡進行預測建模時,各層的連接權值及閾值是隨機初始化的。這種未經優(yōu)化的權值和閾值,會降低人工神經網絡的收斂速度,且容易陷入局部最優(yōu)解。因此,考慮采用遺傳算法對初始權值和初始閾值進行優(yōu)化設計。

3)遺傳神經網絡訓練流程[20-22]。

本文訓練了3個遺傳神經網絡對艦船磁場縱向分量Bx、橫向分量By、垂向分量Bz進行預測。由于結構和訓練過程是相似的,所以僅以Bx預測為例描述該方法。

遺傳神經網絡流程如圖1所示,其主要步驟為:

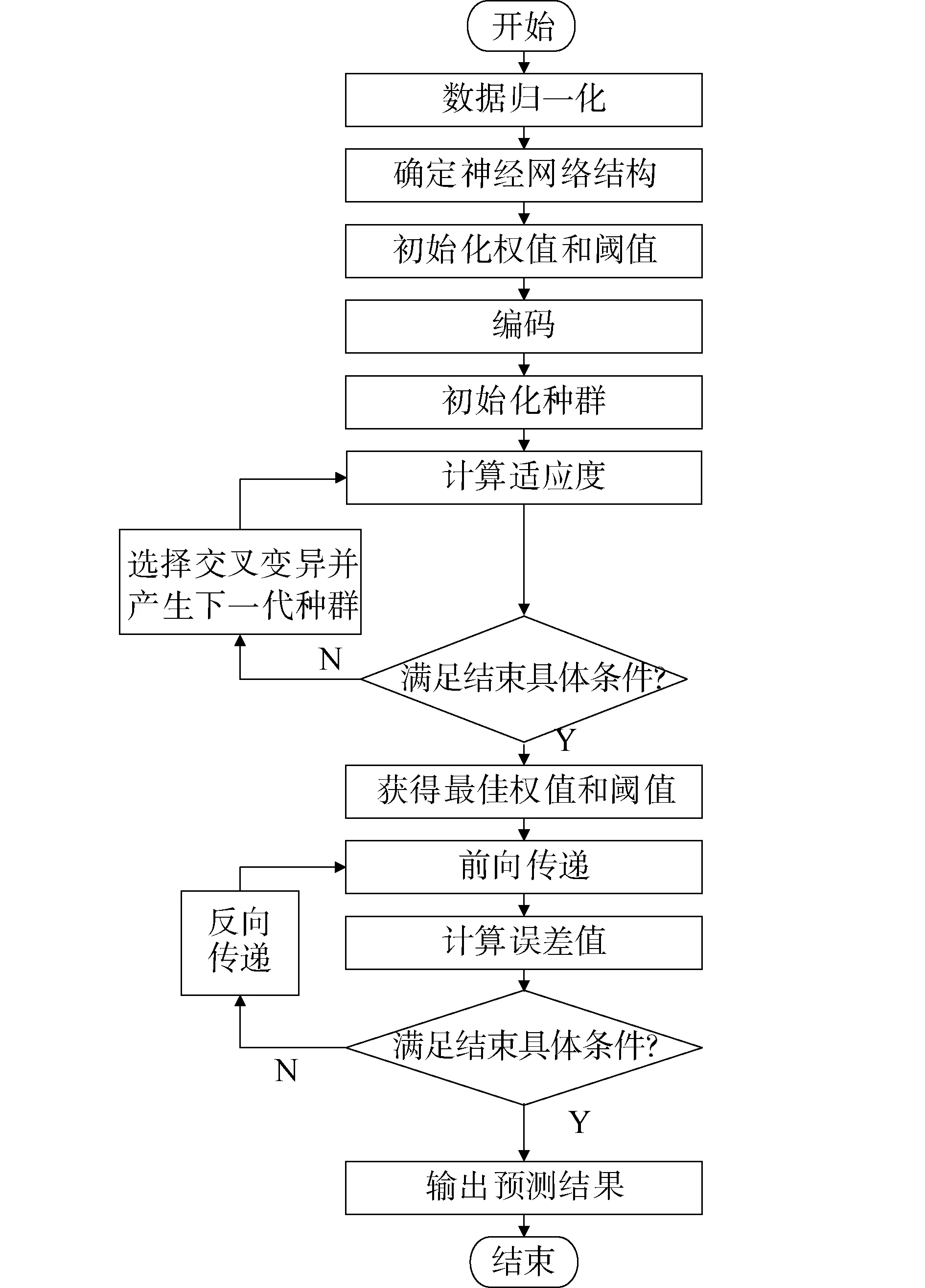
圖1 遺傳神經網絡流程Fig.1 Genetic neural network processes

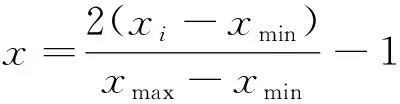
(4)

式中:xi表示輸入或輸出數據;xmax表示數據最大值;xmin表示數據最小值。

2)確定人工神經網絡輸入層、隱含層、輸出層結構。

在本文中,輸入層有3N個節(jié)點,表示設置了N個磁偶極子陣列模擬艦船磁場,每個磁偶極子對應掃描點都有3個空間系數(axji,ayji,azji);輸出層有1個節(jié)點,表示該掃描點的艦船磁場分量Bxj。對于隱含層,通常根據經驗公式,確定隱含層的節(jié)點范圍:

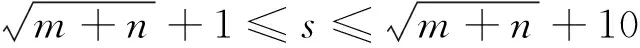
(5)

式中:s為隱含層神經元個數;m和n分別為輸入層、輸出層神經元個數。

在獲得隱含層神經元s范圍的基礎上,運行人工神經網絡,計算不同s值的訓練誤差,把訓練誤差最小時的s值記為隱含層神經元個數。

3)遺傳算法參數初始化。隨機初始化人工神經網絡的權值和閾值,并進行實數編碼,生成用于遺傳算法尋優(yōu)的初始種群。在此基礎上,設置遺傳算法的最大進化代數、交叉概率、變異概率等參數。

4)執(zhí)行選擇、交叉、變異操作,不斷更新遺傳算法的適應度值,達到最大進化代數。適應度值最小的個體被搜索到,得到最佳的初始權值和初始閾值。適應度函數為:

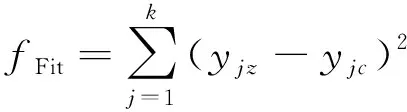
(6)

式中:yjz表示測試集輸出的真實值;yjc表示測試集輸出的預測值;k表示測試集的樣本個數。

5)把遺傳算法優(yōu)化得到的最佳權值和最佳閾值,代入人工神經網絡進行訓練和測試,得到訓練好的模型,算法結束。

2 船模仿真試驗

2.1 數值模型

虛擬艦船船長L=4.2 m,船寬B=0.5 m,建立如圖2所示的空間坐標系。在-1 950 mm≤x≤1 950 mm,y=0,z=0范圍內,等間距設置了21個磁偶極子(“單條線陣列”)作為仿真試驗的等效磁源。

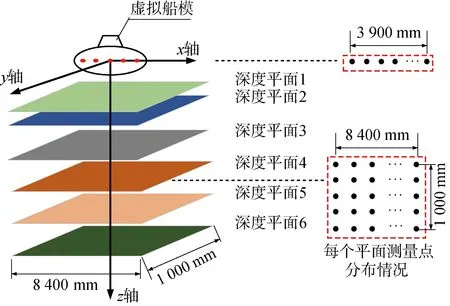
圖2 虛擬船模與6個測量平面Fig.2 Simulated ship model and six measuring planes

在虛擬船模的水線面下方750、1 000、1 500、2 000、2 500、3 000 mm設置6個深度平面。深度平面縱向長度為8 400 mm,縱向間隔100 mm;橫向寬度為1 000 mm,橫向間隔為250 mm,每個深度平面形成包含“5×85”個點陣的測磁陣列。

2.2 仿真訓練過程

通過設置產生6個深度平面的磁場數據,每個深度平面都包含425個測量點,即425個樣本數據。磁場數據包括磁矩計算值、測磁噪聲:

1)磁矩計算值。為了獲得虛擬艦船的磁場數據,另設計了單個旋轉橢球體與5個磁偶極子的混合模型,用于代替該虛擬艦船;通過對該混合模型的磁矩信息進行賦值,可以獲得混合模型在6個深度平面所有測量點的三分量磁場計算數據。其中,每個測量點的縱向分量|Bx|和橫向分量|By|在20 000 nT以內,垂向分量|Bz|在40 000 nT以內。在對混合模型的磁矩信息進行賦值時,相鄰磁矩變化應具有連續(xù)性,不能發(fā)生過強的突變;

2)測磁噪聲。為了模擬真實情況,設定測磁陣列所在空間存在均勻分布的非相關隨機噪聲。取[-10 nT, 10 nT]范圍內的隨機值作為測磁噪聲。

把深度平面1(z=750 mm)和平面2(z=1 000 mm)上的磁場數據作為GNN模型的訓練樣本。同時為了降低GNN的泛化誤差,采用5折交叉驗證方法,把訓練樣本數據隨機分成5等分,每次取一等分做測試集,其余做訓練集,由此可以得到5次試驗的測試集的預測誤差均值,以此控制GNN模型的訓練過程。

在GNN完成訓練以后,把另外4個深度平面上的系數向量輸入訓練好的模型,就可以預測指定平面的三分量磁場數據Bx、By和Bz。

2.3 結果分析

為評估模型預測精度,設相對誤差Eerr為:

(7)

式中:Bpre表示預測值;Bt表示真實值或仿真值。

為了比較2種模型的預測效果,參考傳統(tǒng)等效源模型,由深度平面1、平面2的磁場數據反演建模,并正演預測深度平面3、平面4、平面5、平面6的磁場值Bx、By和Bz。磁場預測結果如表1所示。

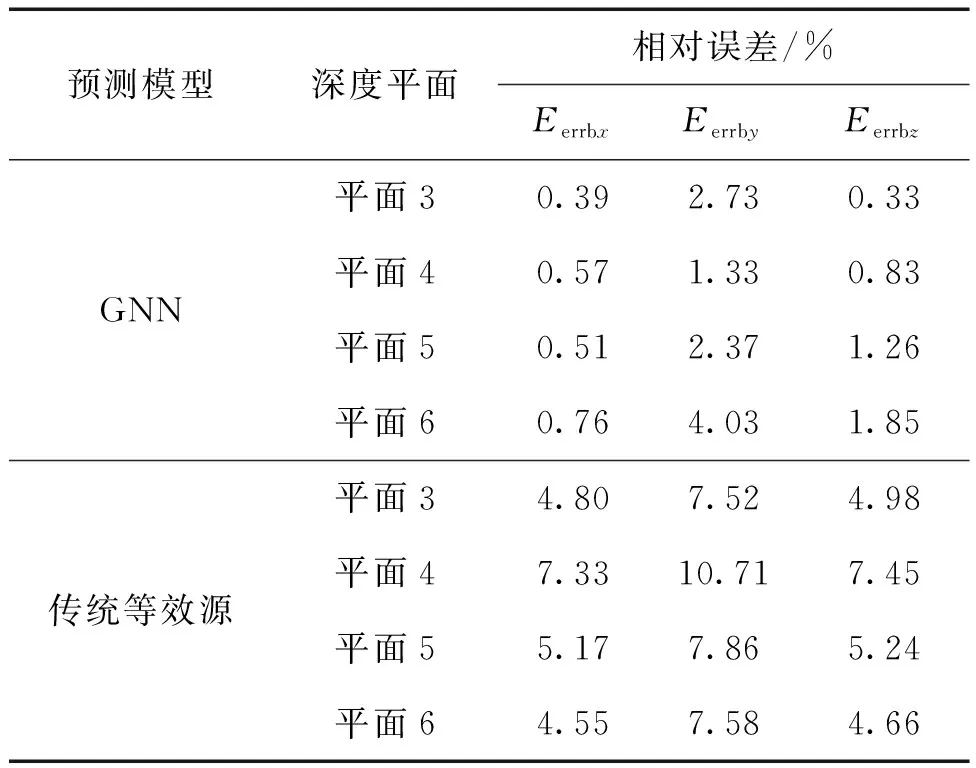
表1 仿真試驗的預測結果Table 1 Prediction results of simulated test

從表1中可以看出:

1)對于GNN模型,預測Bx和Bz時,其在4個深度平面上均具有較高的預測精度,最大相對誤差分別為0.76%和1.85%;預測By時,其在4個深度平面上預測精度較差,最大相對誤差4.03%。

2)在磁源參數設置(數量和位置)相同的情況下,比較GNN與等效源模型對Bx、Bz的預測結果。GNN模型的預測精度均優(yōu)于傳統(tǒng)等效源模型。例如,在對最不利的深度平面6進行預測時,GNN模型對Bx和Bz的預測誤差分別為0.76%、1.85%;傳統(tǒng)等效源模型對Bx和Bz的預測誤差分別為4.55%、4.66%。

3)比較2種模型對By的預測結果,GNN模型的預測精度優(yōu)于傳統(tǒng)等效源模型,但差距不大。以深度平面6的預測結果為例,GNN模型對By預測誤差為4.03%;等效源模型對By的預測誤差為7.58%。

3 物理模型試驗

3.1 實驗設計

選取了磁場實驗室的一條物理模型(船長為L,船寬為B)進行實驗。測磁陣列縱向長度為2L,縱向間隔1/42L(見圖3);橫向寬度為2B,橫向間隔為0.25B,由此形成包括425個點陣的測磁平面,被測艦船位于測磁平面的中心位置。借助升降機調整測磁平面深度,獲得船模下方1.5B、2B、3B、4B共4個深度平面的磁場數據。

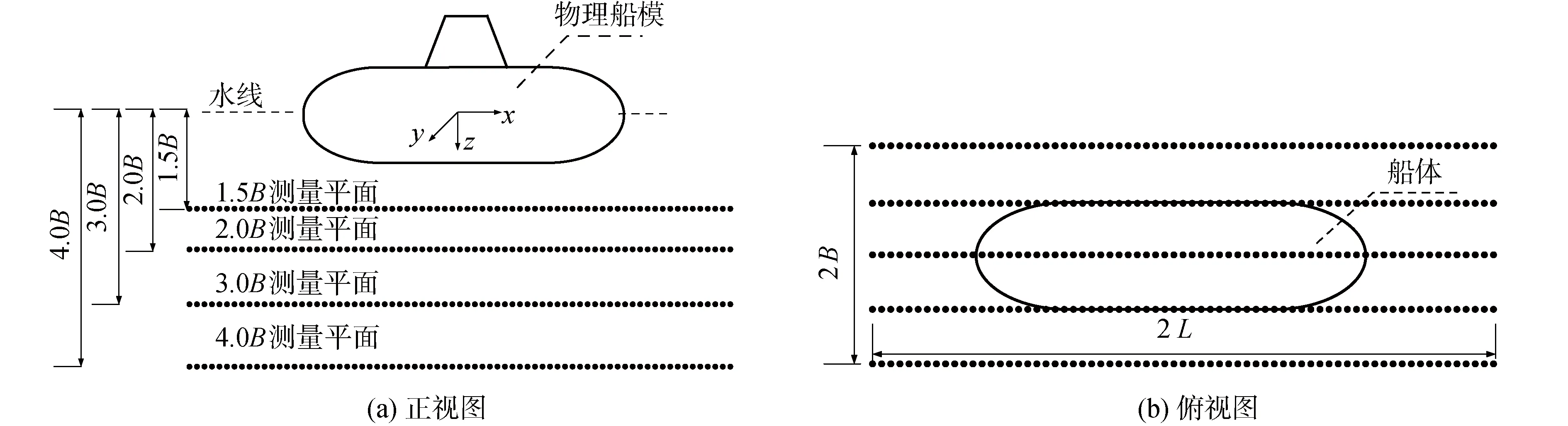
圖3 船模磁場測量面視圖Fig.3 Ship model magnetic field measuring planes views

3.2 遺傳神經網絡訓練過程

不考慮船模的幾何特征,本文僅在水線平面的中線范圍內(-0.5L≤x=≤0.5L,y=0,z=0),等間距均勻設置單條線磁偶極子陣列(簡稱“單條線陣列”),由29個磁偶極子構成,作為等效磁源,如圖4所示。

圖4 單條線磁偶極子陣列Fig.4 Single-line array of magnetic dipoles

把1.5B和2.0B深度平面上的磁場數據作為GNN模型的訓練樣本數據。同時為了降低GNN的泛化誤差,采用5折交叉驗證方法控制GNN模型訓練過程。

在完成上述模型訓練基礎上,分別輸入3B、4B深度平面的系數向量,按照圖1所示流程,預測這3個深度平面的磁場值Bx、By和Bz。

3.3 結果分析

為了比較2種模型的預測效果,又利用傳統(tǒng)等效源模型,由1.5B、2B的磁場數據反演建模,并正演預測3B、4B平面的磁場值Bx、By和Bz。評判標準采用式(3)所示的相對誤差。磁場預測結果如表2所示。

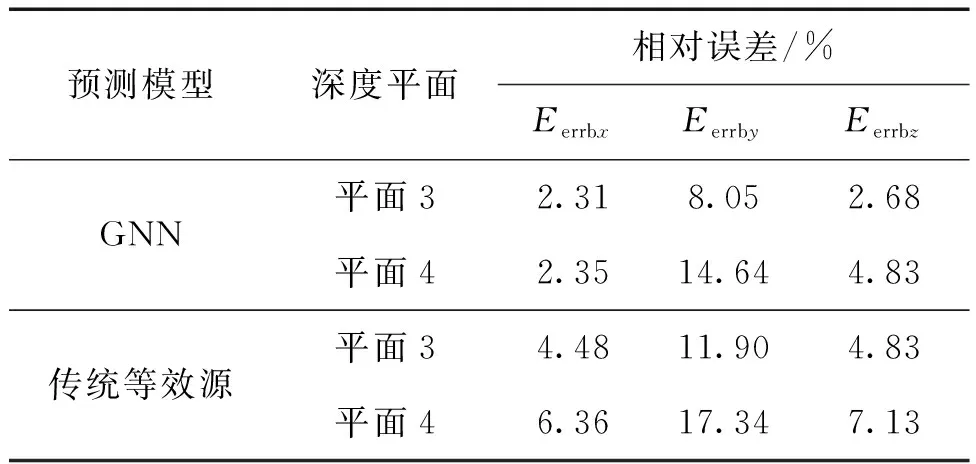
表2 船模試驗的預測結果Table 2 Prediction results of ship model test

從表2中可以看出:

1)預測Bx和Bz時,GNN模型在2個深度平面上預測精度較高,其最大相對誤差分別為2.35%、4.83%。

2)預測By時,GNN模型在2個深度平面上預測精度較差,最大相對誤差14.64%。究其原因,是由于整個測量過程是在南北軌道上完成,船模磁場橫向分量By較小,尤其是龍骨下的By值趨近于0(見圖5),對GNN模型的學習訓練產生不利影響,導致了磁場預測的相對誤差較大。

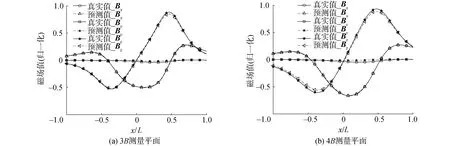
圖5 典型測量線上船模磁場預測值和真實值比較Fig.5 Comparison of predicted and real values of ship model magnetic field on typical measuring point line

3)對2種模型的預測結果進行比較,在預測Bx、By和Bz時,GNN的預測精度均優(yōu)于傳統(tǒng)等效源模型。例如,在對最不利的4.0B深度平面的磁場進行預測時,GNN模型對Bx、By和Bz的預測誤差分別為2.35%、14.64%、4.83%,傳統(tǒng)等效源模型的預測誤差分別為6.36%、17.34%、7.13%。

取船模龍骨下方坐標x=-1L～+1L,y=0,z=+3B,+4B的3條典型測量點線,進行船模磁場預測值與真實值的比較,結果如圖5所示。從圖中可以看出,在預測Bx、By和Bz時,利用1.5B和2.0B的數據進行學習訓練,并預測3.0B、4.0B深度平面的磁場值,吻合度較好,表明GNN模型能夠實現(xiàn)船模磁場的精確預測,且預測精度由于傳統(tǒng)等效源模型。

4 結論

1)本文建立的GNN模型,避免了傳統(tǒng)等效源反演求解的不利影響,實現(xiàn)了船模磁場的準確預測。

2)GNN模型對船模磁場縱向分量Bx、橫向分量By和垂向分量Bz的預測精度均優(yōu)于傳統(tǒng)等效源模型,且隨著訓練樣本的增多,GNN模型的學習能力和預測精度還將進一步提高。

本文的研究結果為下一步開展實船磁場數據建模與預測奠定了基礎。