緩沖包裝不確定性的可靠設計與優化

安雪, 黃博文, 史冬巖

(1.哈爾濱工程大學 機電學院,黑龍江 哈爾濱 150001; 2.羅格斯新澤西州立大學 機械和航天學院,新澤西州 美國 08854)

不確定性問題存在于工程各個領域[1-3],然而,針對包裝工程中的不確定性問題研究相對較少。本文對包裝工程中緩沖防護結構的不確定性展開研究。

產品在搬運和運輸過程中,由于存在諸多不確定因素,例如緩沖包裝材料加工尺寸、產品儲存溫度和運輸條件等,從而導致大量的包裝產品破損[4-6]。為此,人們提出了許多方法保護產品使其遠離損壞的危險。傳統上,減少產品損壞方法是根據ASTM[7]提出的緩沖包裝曲線對產品的緩沖防護結構進行設計。然而這種方法經常出現“過度設計”的情況,造成了材料的經濟浪費。另外,緩沖曲線的確定需要進行大量的跌落實驗,進而對實驗數據進行擬合,數據越多,曲線的擬合精度就約高,浪費了大量的時間成本。這些缺點促使學者引入一種替代傳統跌落實驗的方法,該方法依賴于緩沖包裝材料動態的本構關系[8-9],簡化確定緩沖包裝曲線的過程。然而,動態的本構關系僅對閉孔緩沖包裝材料具有良好的緩沖性能[10],對于開孔的緩沖包裝材料具有一定的局限性。另一種減少產品損壞的方法是對產品的包裝系統進行力學建模,如線性或非線性單自由度或二自由度系統[11-12],通過對產品在跌落過程進行振動響應分析,使產品在跌落時產生的峰值響應加速度降低到產品的脆值(產品的固有屬性)以下。

基于可靠度的優化設計(reliability-based design optimization, RBDO)是解決工程中不確定性的主要手段,得到了廣泛地應用[13]。RBDO概率模型由最小目標函數和概率約束條件組成,以尋求最佳的工程設計,同時降低材料成本[14]。功能度量法(performance measure approach, PMA)[15]和可靠度指標法(reliability-based design optimization,RIA)是求解RBDO概率模型的2大主流方法。RIA方法是求解RBDO概率模型主要技術手段,但當遇到強非線性函數時,RIA方法會產生收斂失敗和數值奇異解的現象[16-17]。

本文通過定義主動集合策略,提出一種改進的RBDO方法,克服了傳統RIA方法的缺點同時解決包裝工程中的不確定性問題。將得到的最優解采用蒙塔卡羅法(Monte-Carlo simulation,MCs)進行驗證,并提供了一種方便簡單的緩沖包裝防護設計方法,實現質量和成本之間的平衡。

1 基于可靠度的優化設計

1.1 RBDO的數學模型

RBDO的數學模型為:

(1)

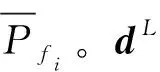
在可靠度理論中,通常采用統計模型來計算系統的失效概率:

(2)

式中fX(x)是X的聯合概率密度函數。式(2)需要求解多維積分得到系統的失效概率。然而,對于大多數實際工程問題,求解多維積分是非常困難的,甚至是不可能完成的。

可靠度指標克服求解多維積分的困難[18],在標準正態空間內原點到功能函數曲面的最短距離,可靠度指標βHL為:

(3)

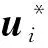
可靠度指標取值均為正,沒有考慮負可靠度指標的情況。因此,可靠度指標的定義是導致RIA方法收斂困難和數值不穩定的主要原因。

1.2 修正的可靠度指標

針對傳統RIA方法不收斂和數值不穩定的現象,本文對傳統可靠度指標的定義進行修正。

本文采用一個邏輯不等式定義一個主動集合策略(active set strategy,ASS)實現對MPP點的過濾和識別,數學表達式為:

(4)

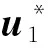
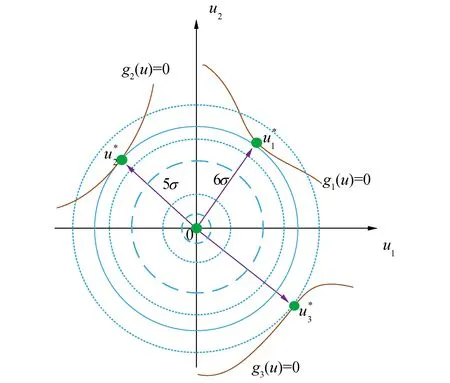
圖1 MPP和±6σ之間的關系Fig.1 The positional relationship between MPP and ±6σ

對于大多數工程問題,如果設計變量落在±3σ范圍內,則認為是可接受的設計,該設計稱為3σ設計。該情況系統的可靠度為99.73%,失效概率為0.27%,如表1所示。然而,由于實際工程系統中存在各種不確定因素的擾動,對于大型復雜的工程結構,3σ設計則被認為是一種不充分和不可靠的設計水平。所以,本文選擇6σ水平設計,其規定范圍相當于99.999 999 8%的可靠度和0.000 000 2%的失效概率,遠遠優于其他設計水平。

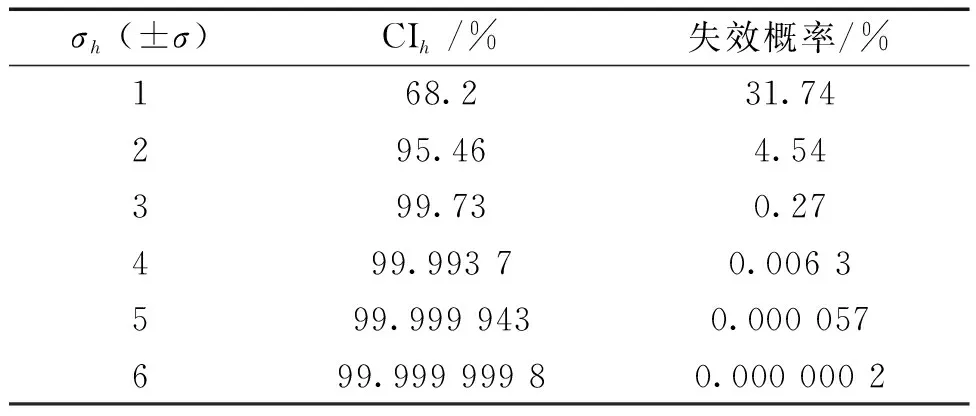
表1 不同的σh對應的CIh和失效概率Table 1 CIh and probability of failure for various σh

修改的可靠度指標重新定義為:

(5)

2 基于主動集合策略的可靠性設計優化方法

在式(1)中定義的RBDO問題,在求解過程通常采用雙循環求解策略,即內循環和外循環,內循環是在獨立的標準正態隨機空間(U-空間)中進行可靠性分析,外循環是在原始物理空間(X-空間)中進行結構優化分析。在本節中,將分別詳細的介紹內循環和外循環,這是本文提出方法的基礎。

2.1 內循環

由于內循環主要是在U-空間執行一個次優化問題來確定MPP和可靠性指標βsj,因此,首先應使用轉化公式將所有隨機變量從最開始的空間轉換為標準正態分布空間,如圖2所示。

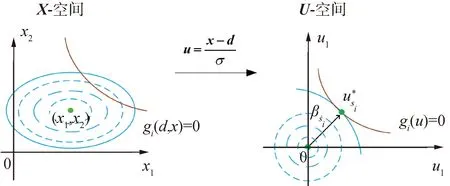
圖2 X空間轉化到U空間Fig.2 The X-space mapping to the U-space

(6)

其次,求解MPP執行的是一個次優化過程,其優化格式表示為:

(7)

式中:gj(u)是第j個有效約束條件的功能函數。借助于MPP后,將概率約束條件使用Rosenblatt[21]變換公式轉化為確定性約束條件:

(8)

式中Φ是標準正態累積分布函數(CDF),因此,

(9)

(10)

根據式(9)和式(10)可以完成約束條件的轉換,式(1)重新寫成:

(11)

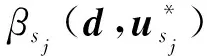
2.2 外循環

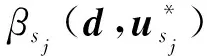
(12)

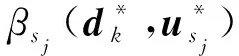
(13)

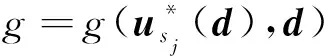
(14)

結合式(5)、(11)和(14)可得到最終的優化迭代格式為:

(15)

在優化開始之前,給出初始設計點d(0)和u(0)。對于每次迭代,首先執行式(7)完成內循環,以求解MPP點和可靠度指標。其次執行式(15)完成外循環,并更新內循環的解,直到程序收斂到最優解。迭代收斂標準‖d(k+1)-d(k)‖/d(k+1)≤ε(ε為給定的極小值),否則,當迭代次數大于允許次數時,則迭代停止。

3 緩沖包裝防護結構的不確定性研究

3.1 包裝系統的跌落模型

包裝件通常由產品,緩沖材料和外包裝箱組成,如圖3所示。將產品和緩沖材料被理想化為具有剛度系數k的無阻尼非線性質量彈簧系統[22-23],本文忽略了外瓦楞紙箱,產品的質量用m表示。

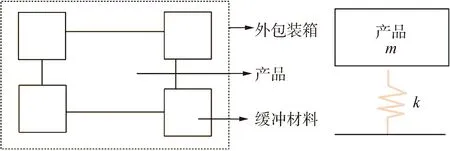
圖3 包裝產品的示意Fig.3 Graphic of a packaged product

包裝系統的跌落模型如圖4所示,其中h為跌落高度,t為緩沖保護材料的厚度。本文采用具有良好的緩沖性能閉孔泡沫聚苯乙烯(EPS)作為緩沖材料[24]。緩沖包裝材料的非線性本構關系是通過壓縮實驗機獲得壓縮數據,并將數據進行多項式擬合確定,實驗裝置如圖5和6所示。

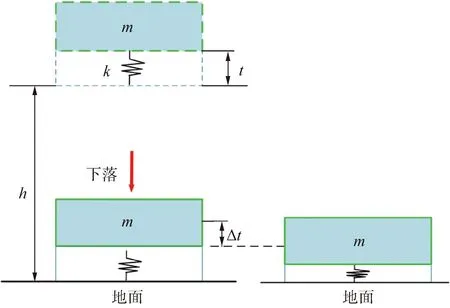
圖4 模型與地面撞擊過程Fig.4 The process of collision between model and the ground

圖5 壓縮試驗機5566Fig.5 Instron 5566

圖6 緩沖材料和壓盤Fig.6 The cushion material and platen

3.2 跌落過程中的能量分析

在跌落過程中,當包裹與地面碰撞時,緩沖包裝材料被壓縮為動態非線性變化過程。假設在動態沖擊過程中,沖擊產生的能量全部被緩沖材料吸收并使其變形最大不再傳遞到外界(忽略摩擦力的影響)。因此,本文以產品m為研究對象,由能量平衡得:

(16)

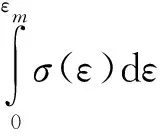
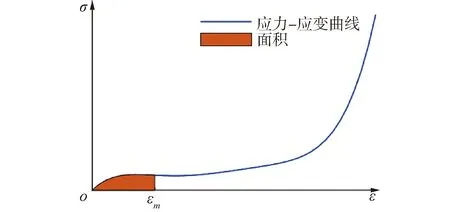
圖7 動態的應力-應變曲線Fig.7 Dynamic stress-strain curve

進而計算出產品的最大加速度為:

amax=σ(εm)A/m

(17)

3.3 RBDO 數學模型

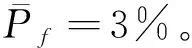
(18)

在本文中,初始設計點設置為d(0)=0.05和u(0)=0。優化收斂標準為ε=10-6,且給定的最大迭代步數是200次。

應用本文提出的ASS方法對上述數學模型進行計算求解。在評估概率約束的過程中需要迭代18次,收斂得到的最優解為0.036 0,其迭代過程如圖8所示。此外,應用MCs驗證最優解,隨機抽取2×106個樣本點對失效概率進行評估,2個約束的失效概率均在允許的失效概率(3%)內。因此,ASS解決了緩沖防護結構的厚度不確定性問題,并提供了緩沖包裝防護結構的最佳厚度尺寸是0.036 0 m。

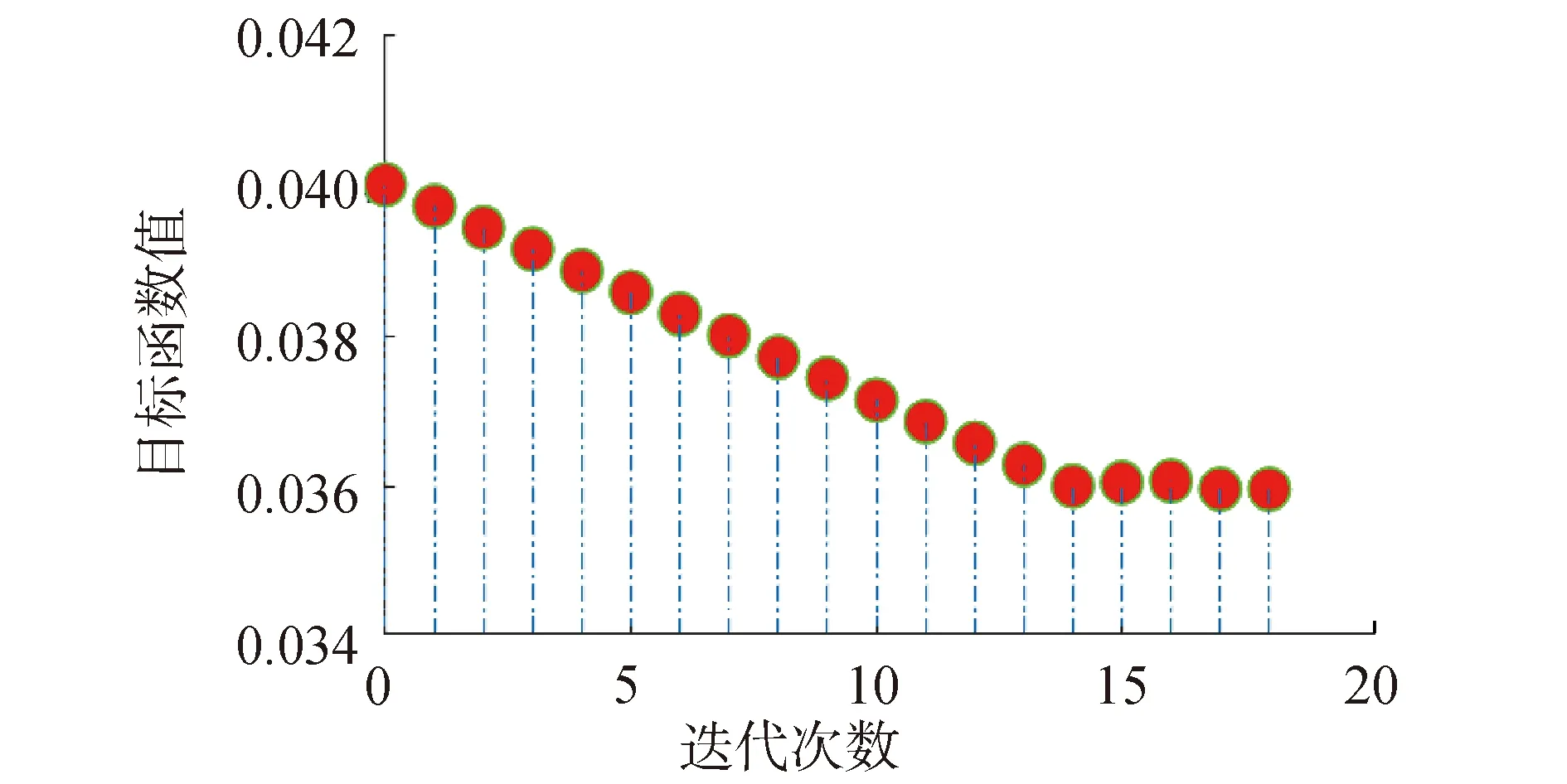
圖8 迭代過程Fig.8 The process of iteration

4 結論

1)本文提出基于主動集策略的可靠度優化方法。通過在內循環中使用一個邏輯的不等式引入了主動集合策略對傳統可靠度指標的定義進行修正,解決了傳統RIA方法收斂困難和數值奇異性問題。

2)本文提出的ASS方法解決了包裝工程中的不確定性問題。該方法充分考慮了緩沖包裝防護結構厚度幾何尺寸的不確定性因素,基于能量守恒建立了緩沖包裝防護結構動態非線性的本構關系模型,通過將不確定性進行量化,構造了RBDO概率模型,并運用本文提出的方法計算出了全局最優解。最后,采用MCs方法對最優解進行驗證,結果表明計算出的最優解是正確并且是合理的。

3)本文提出的方法為緩沖包裝防護結構的輕量化設計和可靠性設計提供了理論支撐。