機器學習在航空發動機排氣溫度預測中的應用研究*

易文川 王 興 王 翔 唐慶如

（1.中國民用航空飛行學院航空工程學院 廣漢 618307）（2.中國民用航空飛行學院工程技術訓練中心 廣漢 618307）

1 引言

離開燃燒室的氣體混合物的溫度是優化發動機性能和控制排放的關鍵參數，這是因為排氣溫度（Exhaust Gas Temperature，EGT）與氣缸內的燃燒過程密切相關［1］。EGT 影響排放控制系統的性能。例如，不完全燃燒產物（如一氧化碳和未燃燒碳氫化合物）的催化氧化需要EGT 大于250℃［2］。此外，EGT還可以用于發動機故障診斷和維護，以延長發動機壽命［3～5］。因此，在發動機運行期間預測EGT十分重要。

文獻中發表了幾種可以預測給定操作條件下EGT 的物理模型［6～7］。一般來說，物理模型包括缸內燃燒模型、傳熱模型和排氣模型。然而，在燃燒后期發生的復雜現象［8］可能使傳統物理模型難以準確預測EGT。如果考慮基于數據驅動的預測模型，采用機器學習算法來模擬燃燒過程、傳熱過程和排氣冷卻過程，則可以降低預測EGT 的復雜性。文獻綜述表明，相關模型已成功用于預測EGT［9～14］。總的來說，這些方法支持使用機器學習技術來構建快速、穩健的基于數據驅動的EGT 預測模型，進而協助或替代物理預測模型。盡管EGT 在發動機開發中很重要，但文獻中使用機器學習技術預測EGT的研究數量有限，因此本文的目標是研究基于數據驅動的機器學習預測模型在預測EGT 方面的性能。鑒于難以為該任務先驗地選擇最合適的機器學習算法，評估了不同算法的預測性能，即人工神經網絡（Artificial Neural Network，ANN）、隨機森林（Random Forest，RF）、支持向量回歸（Support Vector Regression，SVR）和門控循環單元（Gate Recurrent Unit，GRU）?？偟膩碚f，本文的結果有助于優化發動機性能、排放和壽命，同時能夠對從事相關研究的學者有一定的借鑒意義。

2 機器學習算法簡介

2.1 人工神經網絡

基于數學計算，神經網絡算法使用一組相互連接的人工神經元在發動機關鍵性能參數（燃油流量、滑油壓力和轉速）和排氣溫度之間建立非線性關系。如圖1 所示，該模型使用了帶反向傳播算法（此處未顯示）的3-N-1架構，隱藏層與輸出層的傳遞函數分別為tansig和purelin。盡管在三層網絡結構中沒有選擇隱層神經元數量N 的一般規則，文獻［15］建議N=2n+1，n為輸入變量的個數。

圖1 人工神經網絡模型示意圖

神經元是人工神經網絡的基本處理單元，執行兩個功能：收集輸入和生成輸出。輸入和輸出之間的關系為

其中，wi為第i個輸入Ii的權重；b為偏置；f(·)為激活函數；O為神經元的輸出。多層前饋網絡具有多層結構的神經元，可以在沒有反饋連接的情況下單向傳遞信息。第l+1層的神經元j可表示為

其中，nij為第l層的所有神經元；wlij為連接第l層神經元i和第l+1 層神經元j的權重；blj為第l層神經元j的偏置。

反向傳播算法通常用于訓練前饋神經網絡，它有規則地調整每個訓練模型的權重，以最小化網絡預測值與實際值之間的誤差。在監督學習的過程中神經網絡通過迭代的方式學習樣本特征。訓練網絡需要設計合適的網絡結構（如隱藏層的層數、每一層神經元的個數等）和超參數（如初始化權重、學習率、正則化參數等）以防止過擬合。

2.2 隨機森林

與神經元和人工神經網絡之間的關系類似，決策樹是隨機森林算法的基本處理單元。圖2 顯示決策樹表示一組約束或條件，這些約束或條件按層次組織并從樹的根依次應用到終端節點。在處理回歸問題時，從數據集中執行遞推分割和多元回歸以形成決策樹。從根節點開始，在樹的每個內部節點中重復進行數據分割過程，直到達到之前指定的停止條件。每個終端節點或葉節點都有一個僅適用于該節點的簡單回歸模型。樹的分枝過程一旦完成，就可以進行剪枝，目的是通過降低樹的結構復雜性來提高樹的泛化能力。

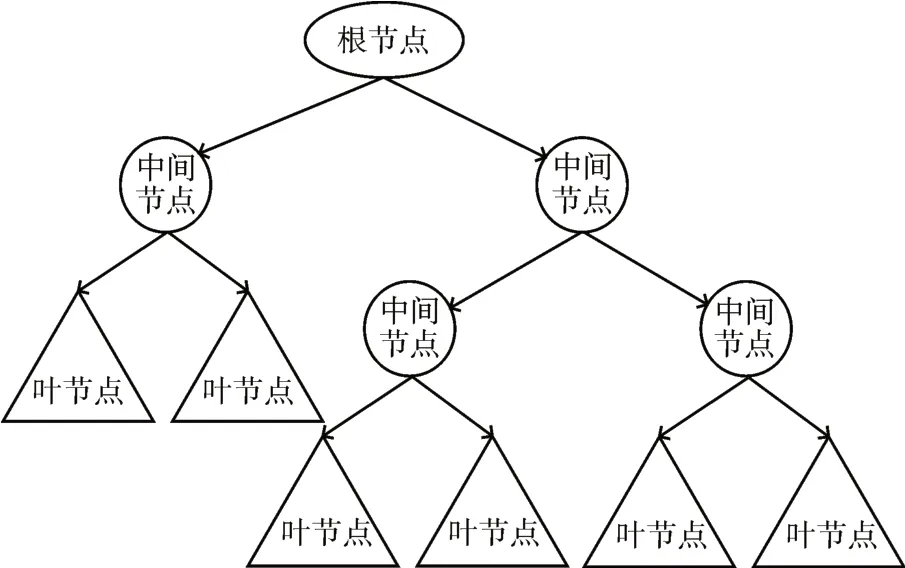
圖2 決策樹示意圖

在決策樹的形成過程中，決策樹在所有候選分枝中搜索最佳分枝，以最小化結果樹的“雜質”：其中，s是節點t處的候選分枝，i(t)為分枝前的“雜質”度量，Δi(s，t)為分枝后的“雜質”減少量。在該等式中，節點t被劃分為左子節點tL（比例為PL）和右子節點tR（比例為PR）。基尼指數（Gini index，GI）通常用以衡量“雜質”：

其中，f(tX(xi)，j)表示值為xi的樣本屬于葉節點j和中間節點t的比例，決策樹以最小化基尼指數作為分枝標準。

隨機森林是一種回歸技術，它結合了眾多決策樹算法的性能來分類或預測變量的值。如果隨機森林基于輸入矢量{x} 構建了K個決策樹，那么隨機森林預測模型表示為

其中，Tk(x)為第k個決策樹的預測，為所有決策樹預測的平均值。

2.3 支持向量回歸

支持向量機的基本思想是將輸入特征轉換為一個高維空間，其中兩個類別可以由一個高維曲面線性分離，稱為超平面［16］。假設一個訓練數據集有N個樣本和L個輸入特征，對應于已知的輸出特征，支持向量回歸模型定義如下：

其中，φ是將輸入數據映射到高維特征空間的非線性函數；w是垂直于超平面的權重矢量；b為超平面偏置。在軟邊界約束下，支持向量回歸模型的優化定義了一個超平面，該超平面將具有最大邊界的訓練數據分離。該優化問題可以使用拉格朗日乘數法（Lagrange multiplier method）求解：

其中，γ為核參數。支持向量回歸沒有設計映射函數、轉換數據并計算內積，而是直接將內核定義為輸入特征向量的函數。通過引入核表示法，極大簡化了該代價函數的優化問題。

2.4 門控循環單元

循環神經網絡（Recurrent Neural Network，RNN）在處理時間序列數據時優勢明顯，作為RNN 的一種變體，長短期記憶網絡（Long Short Term Memory，LSTM）增加了一種攜帶信息跨越多個隱含層的方法，從而防止較上層的信息在傳遞過程中逐漸失真。但LSTM 的隱含層結構復雜，訓練樣本的時間過長。門控循環單元在結構上簡化了LSTM 網絡的門設置，圖3為門控循環單元示意圖。

圖3 門控循環單元示意圖

圖中，⊙表示矩陣點乘；⊕表示矩陣相加；Tanh為激活函數，將數據縮放到(-1 ～1) 的范圍內；xt為t時刻的輸入；ht-1、ht分別為上一節點傳遞下來的隱狀態和當前節點的隱狀態；r、u分別為重置門和更新門。門控更新過程為

其中，rt、ut分別為t時刻重置門與更新門的狀態；Wr、Wu、Wh′、Wy為學習的參數矩陣；h'、yt分別為當前節點的中間狀態和模型輸出；σ為sigmoid函數；*代表矩陣點乘。第t個節點的隱藏狀態聚集了前t個時間步的信息，用當前輸入xt和上一節點傳遞下來的隱藏狀態ht-1進行建模。

3 數據說明及預處理

筆者的前期工作收集了同一架次Cessna-172R 型飛機（使用一臺活塞式發動機，型號為IO-360-12A）在約400次飛行訓練過程中的機載傳感器數據，傳感器以離散形式記錄數據，數據刷新頻率為1Hz。該數據集記錄了反映飛機當前性能和狀態的52種飛行參數，其中包括7種與發動機直接相關的飛行參數，即油箱油量（FQty）、滑油溫度（OilT）、燃油流量（FFlow）、滑油壓力（OilP）、轉速（RPM）、缸頭溫度（CHT）和排氣溫度（EGT），實測數據部分展示如表1所示。

表1 實測數據

由于過擬合會給機器學習模型的訓練帶來誤差，因此需要進行特征子集選擇。皮爾遜相關系數通常用來衡量特征之間的相關性［17］，7 種飛行參數之間的皮爾遜相關系數如圖4 所示。本文以燃油流量、滑油壓力和轉速作為輸入，以建立用于預測EGT的機器學習模型，因為這些參數與EGT高度相關［18］。

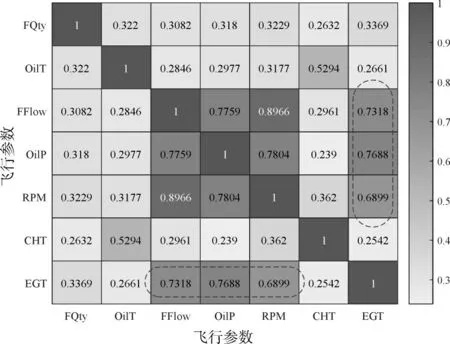
圖4 飛行參數之間的相關系數

大約80%的數據用于訓練機器學習模型，其余20%用于測試EGT 預測模型的性能。在評估機器學習模型性能期間，根據預測值與實際值之間的差異計算均方根誤差（RMSE），以確定預測的精度和偏差。此外，決定系數（R2）用以衡量預測值與實際值的擬合優度。在統計學中，接近1 的R2和接近0的RMSE表示良好的預測性能。

4 機器學習算法性能評估

4.1 機器學習算法在預測EGT中的性能比較

本文使用貝葉斯優化方法獲得機器學習模型的最佳超參數。貝葉斯優化已成為支持向量機或深度神經網絡等機器學習算法超參數優化的成功工具。該算法在目標函數內部模擬高斯過程模型，通過評估目標函數來訓練該模型［19］。貝葉斯超參數優化后，機器學習模型的一些關鍵超參數如表2所示。

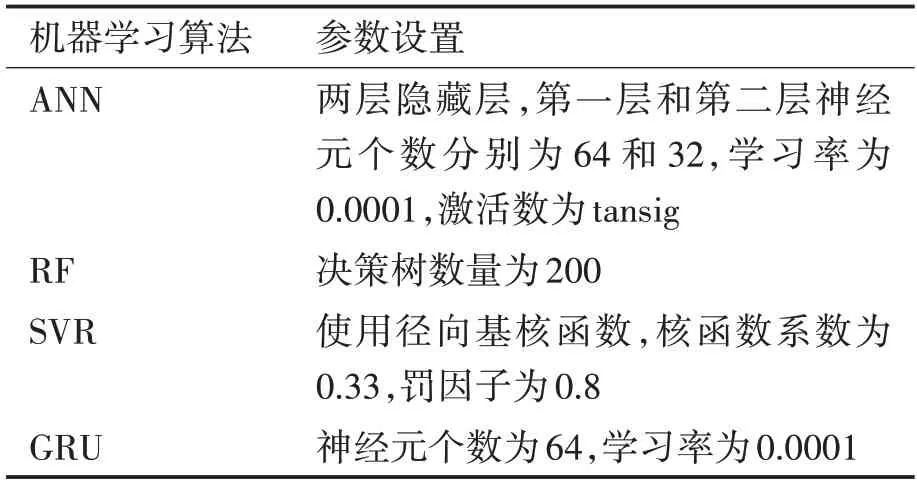
表2 機器學習算法關鍵超參數設置

超參數優化后訓練機器學習模型，并在測試數據上驗證EGT 預測模型的性能，結果如圖5 所示。實際EGT和預測EGT分別繪制在x軸和y軸上。圖5 表明預測存在可接受的偏差。為了幫助評估圖5中的模型性能，陰影區域覆蓋了誤差在±1%（約為12deg F）以內的預測數據，幾乎所有的點都聚集在45°對角線上。值得一提的是，接近1 的斜率和接近0的RMSE表明三個模型輸入（即燃油流量、滑油壓力和轉速）足以預測EGT。

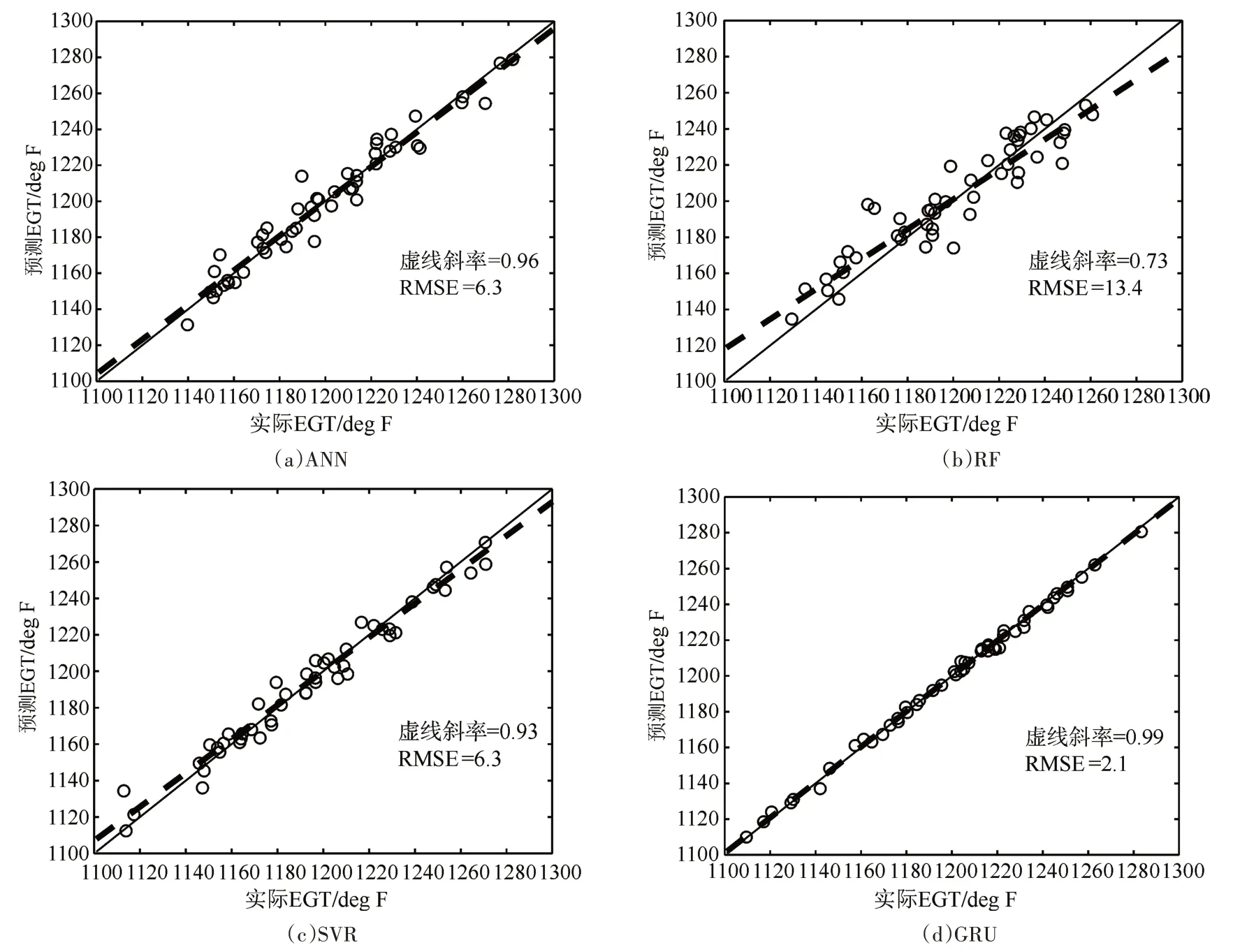
圖5 機器學習模型預測性能

顯然，GRU、ANN 和SVR 的預測性能優于RF，這表現在陰影區域內的點更多、斜率更接近1 且RMSE 更小。此外，RF 高估了EGT 較低的情況，但低估了EGT 較高的情況。盡管RMSE 和陰影區域內的點數幾乎相同，但ANN 的表現略優于SVR，這可以通過更接近1 的斜率來證明。GRU 在這四種算法中表現最好，因為圖5（d）中陰影區域內的點幾乎成線性分布。

圖6 在擬合優度上比較了四種機器學習模型的EGT 預測性能，此外，以每秒鐘機器學習模型訓練的樣本數（samples per second，SPS）來衡量模型復雜度并給出對比結果。

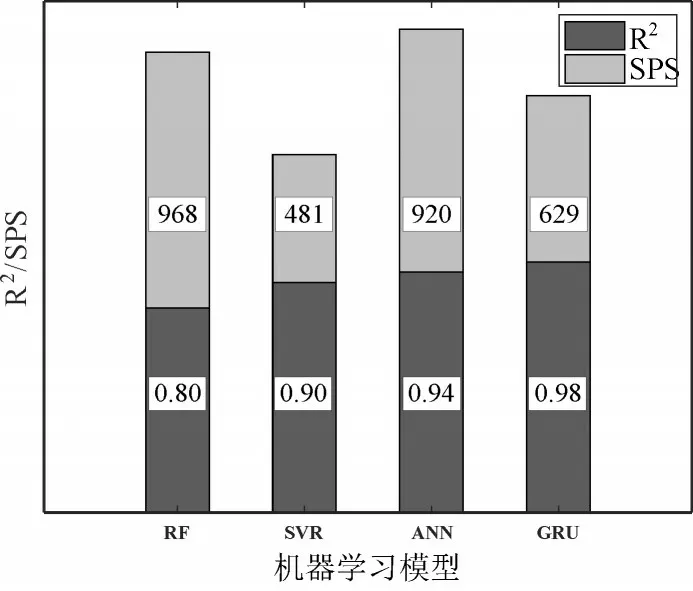
圖6 模型的預測性能與復雜度對比

從擬合優度上評估模型預測性能，GRU 預測EGT的準確性最高，而RF算法的準確性最低，這與圖5 得出的結論一致。然而，RF 算法的計算效率最高，與之相反，SVR 的計算效率最低但保證了較好的預測精度。如果經過良好訓練，ANN 是最合適的EGT 預測算法，在預測精度和計算效率上均表現優異，這在EGT 實時預測時尤其重要。然而，ANN 在正確調整其超參數方面需要大量努力。

4.2 機器學習算法的抗噪能力

評估機器學習算法的抗噪能力也很有意義。實際情況下，數據樣本中摻雜噪聲信號是不可避免的，噪聲信號的強弱將影響EGT 預測的準確性［20］。本文對模型的輸入樣本添加不同功率的噪聲信號，用以模擬發動機在真實飛行環境下可能受到擾動而導致傳感器記錄的數據產生噪聲。原始數據與噪聲的功率比用信噪比（Signal to Noise Ratio，SNR）來描述：

其中，x(t)為原始數據；n(t)為噪聲。在不同的信噪比條件下，對四種機器學習模型的EGT預測性能進行評估，結果如圖7 所示。一般來說，所有機器學習模型的預測性能都隨著信噪比的增加而提升，當信噪比在9dB～21dB 時，所有模型的預測性能顯著提升。對于SNR 在15dB～30dB 的情況，GRU 在所有機器學習模型中表現最佳，但信噪比低于18dB 時，隨著信噪比的降低，GRU 的預測性能快速下降，信噪比低于12dB 時，它的表現最差。因此，GRU 保證高預測性能的前提是模型輸入需要高質量的無噪聲數據。此外，在低信噪比（小于15dB）條件下，ANN 的預測性能優于其他機器學習模型。

圖7 不同信噪比條件下機器學習模型的預測性能

4.3 機器學習算法的魯棒性與泛化能力

為了說明機器學習算法的魯棒性與泛化能力，從整個數據集中多次隨機劃分訓練集和測試集，對文中提到的模型進行多次訓練與測試。

圖8（a）顯示了使用四次隨機選擇的80%數據訓練后的機器學習模型擬合優度。結果表明，無論訓練集如何，機器學習模型都表現良好，相似的R2證明了這一點。在監督訓練后，對其余20%數據進行EGT 預測。圖8（b）表明，無論是在訓練集還是測試集，機器學習模型都表現出了相似的擬合優度，這說明模型的預測性能從訓練集泛化到測試集。總的來說，RF、SVR、ANN 和GRU 均是穩健EGT預測算法。

圖8 分析機器學習模型的魯棒性與泛化能力

5 結語

在燃燒后期發生的復雜現象可能使傳統物理模型難以準確預測EGT。本文的目的是研究當使用燃油流量、滑油壓力和轉速作為模型輸入時，用實測數據訓練的機器學習模型是否有助于EGT 預測。鑒于難以為該任務先驗地選擇最合適的機器學習算法，評估四種經典機器學習回歸算法在預測EGT方面的性能，即人工神經網絡、隨機森林、支持向量回歸和門控循環單元。主要結論如下：

1）四種機器學習模型在可接受的誤差范圍內預測了排氣溫度，這表明三個模型輸入（即燃油流量、滑油壓力和轉速）足以預測EGT。

2）模型性能相互比較時，門控循環單元的預測精度最高，但它通常需要高質量的無噪聲數據；隨機森林的精確度最低，但需要的計算資源最少；支持向量回歸在耗費高計算資源的前提下保證了較好的預測精度；人工神經網絡是最合適的預測算法，但它存在繁瑣的超參數調整過程。