一種雙層圓孔陣列全介質超表面完美吸收器

許瑞星,呂曉龍,郭云勝

(內蒙古科技大學 理學院,內蒙古 包頭 014000)

全介質超表面與金屬超表面相比,具有耐高溫、耐腐蝕、歐姆損耗低等優點[1-3],在無線通信[4]、寬帶吸收[5]、濾波器[6]、頻率選擇[7]、傳感[8-9]、天線[10]和生物醫學[11-12]等領域有廣泛的應用。2016 年,Michael 等提出全介質惠更斯超表面完美吸收器[13],開啟了全介質超表面在吸波領域的重要應用。一般而言,把具有適當損耗的高介電常數圓柱體周期性地嵌入到低介電常數材料中,調整圓柱體高度與直徑的比值,使入射電磁波在介質圓柱內激發的電偶極子和磁偶極子諧振于同一頻率,反射率和透射率都會變為零,從而實現了全介質惠更斯超表面的完美吸收。為了驗證上述理論,Liu 等采用絕緣襯底上的硼摻雜硅工藝制作了太赫茲波段實驗樣品,測試結果表明在1.011 THz 處吸收率為97.5%,與完美吸收的微小差距是由樣品的粗糙度造成的[14]。2017 年,Ming 等基于簡并臨界耦合理論進一步闡述了惠更斯超表面完美吸收器的工作原理[15],為設計完美吸收超表面提供了充足的理論依據。

然而,對于完美吸收全介質超表面實驗樣品的制備而言,采用硅摻雜工藝在襯底材料上制作具有一定損耗的諧振器,存在難度大、周期長、成本高等問題,嚴重限制了全介質超表面的應用。考慮到微波段完美吸收超表面在電磁隱身和屏蔽等方面具有較大的應用前景[16-19],本文探究一種微波段全介質超表面完美吸收樣品的簡單結構和制作方法。研究結果表明,由損耗較大的磁性復合材料吸波片和損耗極小的聚四氟乙烯陶瓷復合材料組合成雙層基板,在其上排列的周期性圓孔陣列能夠實現惠更斯全介質型超表面的近似完美吸收。

1 模型與仿真

本文采用Comsol Multiphysics 軟件對圓孔陣列全介質超表面進行仿真。一般而言,電磁波在某個頻率處的完美吸收與超表面結構的幾何和材料參數有極大關系。為尋找圓孔陣列超表面實現完美吸收的一般規律,首先在一定材料參數的介質板上設計圓孔陣列結構,通過優化圓孔結構的幾何參數,使超表面在外界電磁波的激發下產生的電偶極子和磁偶極子在同一頻率處諧振;然后優化材料損耗,找出完美吸收所需的最佳值,從而完成了超表面完美吸收樣品的設計。圖1(a)為構建的介質圓孔陣列超表面樣品的單元結構,其中P和D分別是單元結構的周期和直徑,t是圓孔的厚度。圖1(b)是單元結構在xy平面上的 3×3 陣列。圖1(a)的仿真模型中,波矢量沿z方向,電場沿x方向;與x和y方向垂直的平面分別設置為周期性邊界條件,與z方向垂直的兩個平面設置端口。在超表面樣品設計中,通過反射系數S11和透射系數S21計算得出反射率R(ω)=和透射率T(ω)=,可得到吸收率A(ω)=1-R(ω)-T(ω) 隨樣品的幾何和材料參數的變化情況。

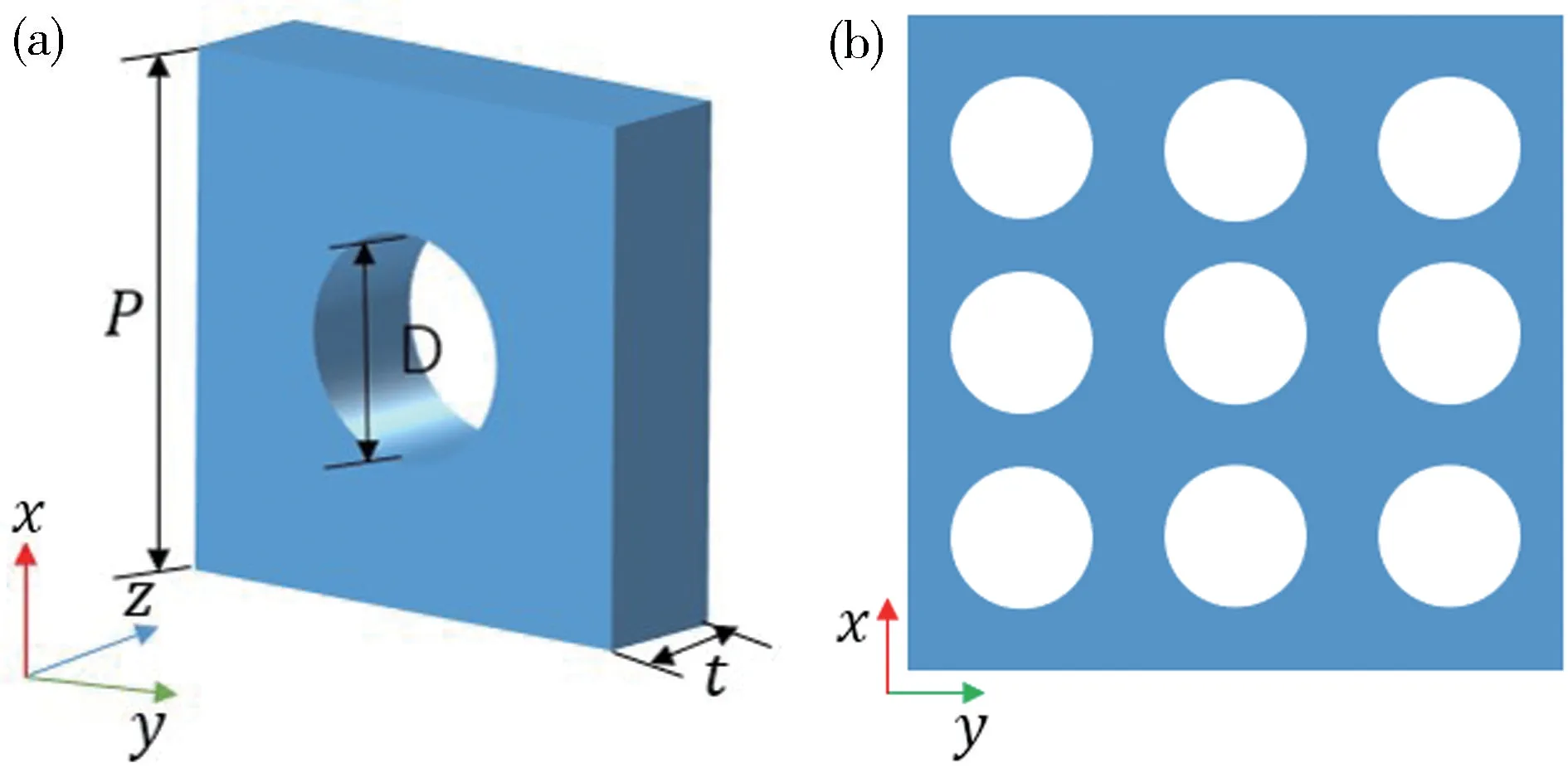
圖1 (a)全介質超表面的單元結構;(b)超表面單元在xy 平面的 3×3 陣列Fig.1 (a) Cell structure of all-dielectric metasurface;(b) 3× 3 array of metasurface units in the xy plane

圖1(a)中單元結構的大小為16 mm,厚度為5 mm,介質材料的相對介電常數為11,介質損耗角正切為0.03,吸收率隨圓孔直徑D的變化規律如圖2(a)所示。從圖2(a)可清楚地看出,當圓孔直徑從11.2 mm 變化到15.2 mm 時,從低頻段開始出現的兩個吸收峰逐漸合并為一個峰,然后又逐漸分離。以圓孔直徑為11.2 mm 的兩個吸收峰為例,分析它們的電磁諧振模態可知,9.8 GHz 處的吸收峰為電諧振峰,其模態的電場與電偶極子[20-22]相似,如圖2(b)所示;11 GHz 處的吸收峰為磁諧振峰,其模態的磁場與磁偶極子[20-22]相似,如圖2(c)所示。當圓孔直徑為13.2 mm時,電諧振峰和磁諧振峰在11.3 GHz 處重疊。由于介質損耗不是最佳值,諧振峰重疊處的吸收峰僅為75.3%。

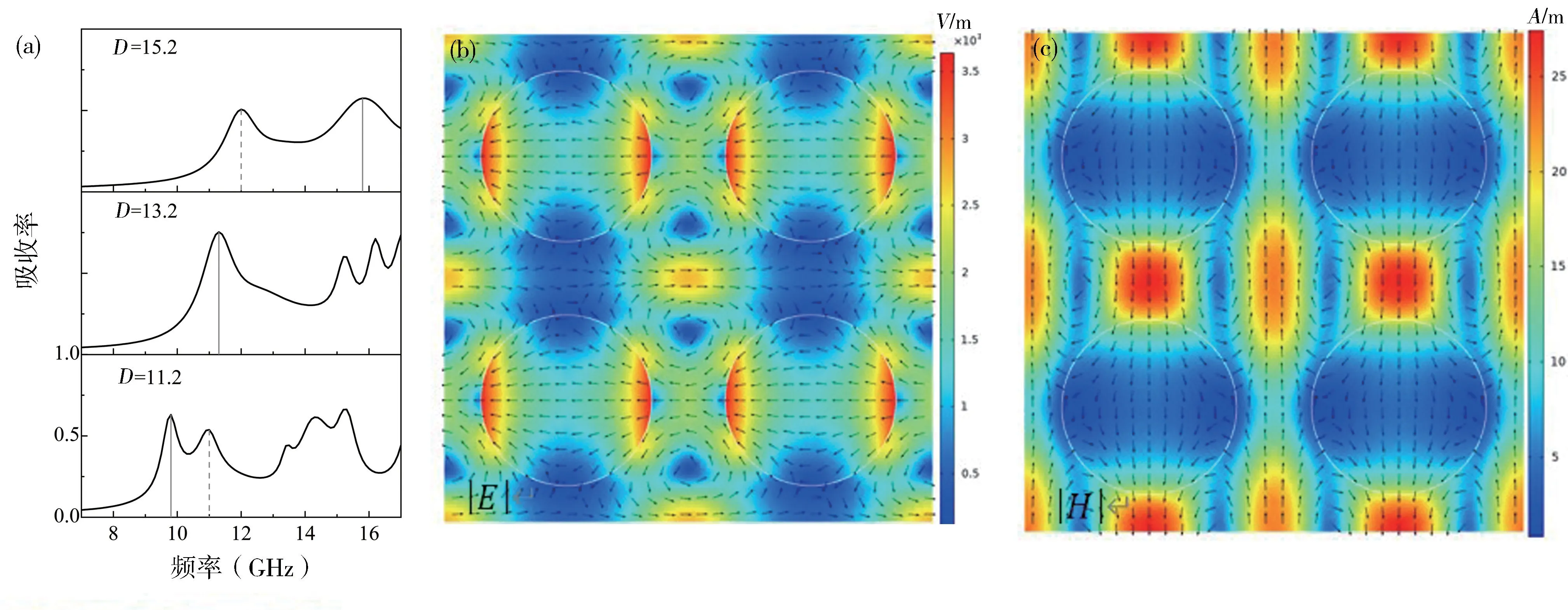
圖2 (a)圓孔直徑不同的情況下,超表面的吸收譜中電諧振峰(垂直實線)和磁諧振峰(垂直虛線)的變化;圓孔直徑D=11.2 mm 時(b)9.8 GHz 處的電場模和(c) 11 GHz 處的磁場模Fig.2 (a) Variation of the electric (vertical solid line) resonance peaks and magnetic (vertical dashed line)resonance peaks in the absorption spectrum of the metasurface for different circular hole diameters;(b) Electric field mode at 9.8 GHz and (c) magnetic field mode at 11 GHz when the circular hole diameter D is 11.2 mm

固定圓孔直徑為13.2 mm,優化介質損耗角正切值,吸收率隨損耗角正切的變化結果如圖3(a)所示,可以看出: 介質損耗角正切值從0.05 變化到0.15,在11.3 GHz 處的吸收率先增大后減小;當介質損耗角正切tanδ=0.1 時,接近于完美吸收(99.95%)。另外,為了驗證圓孔陣列是實現超表面完美吸收的關鍵因素,對無圓孔陣列介質平板進行仿真對比。介質平板的厚度和材料參數與圓孔陣列超表面中的相應參數完全相同,材料的介質損耗角正切變化范圍也相同。介質平板對電磁波的吸收率隨介質損耗角正切變化的規律如圖3(b)所示。從圖3(b)中可清楚地看出,當介質損耗角正切值逐漸增大時,介質平板的吸收率都較低,因此圓孔結構對超表面實現完美吸收起到關鍵作用。

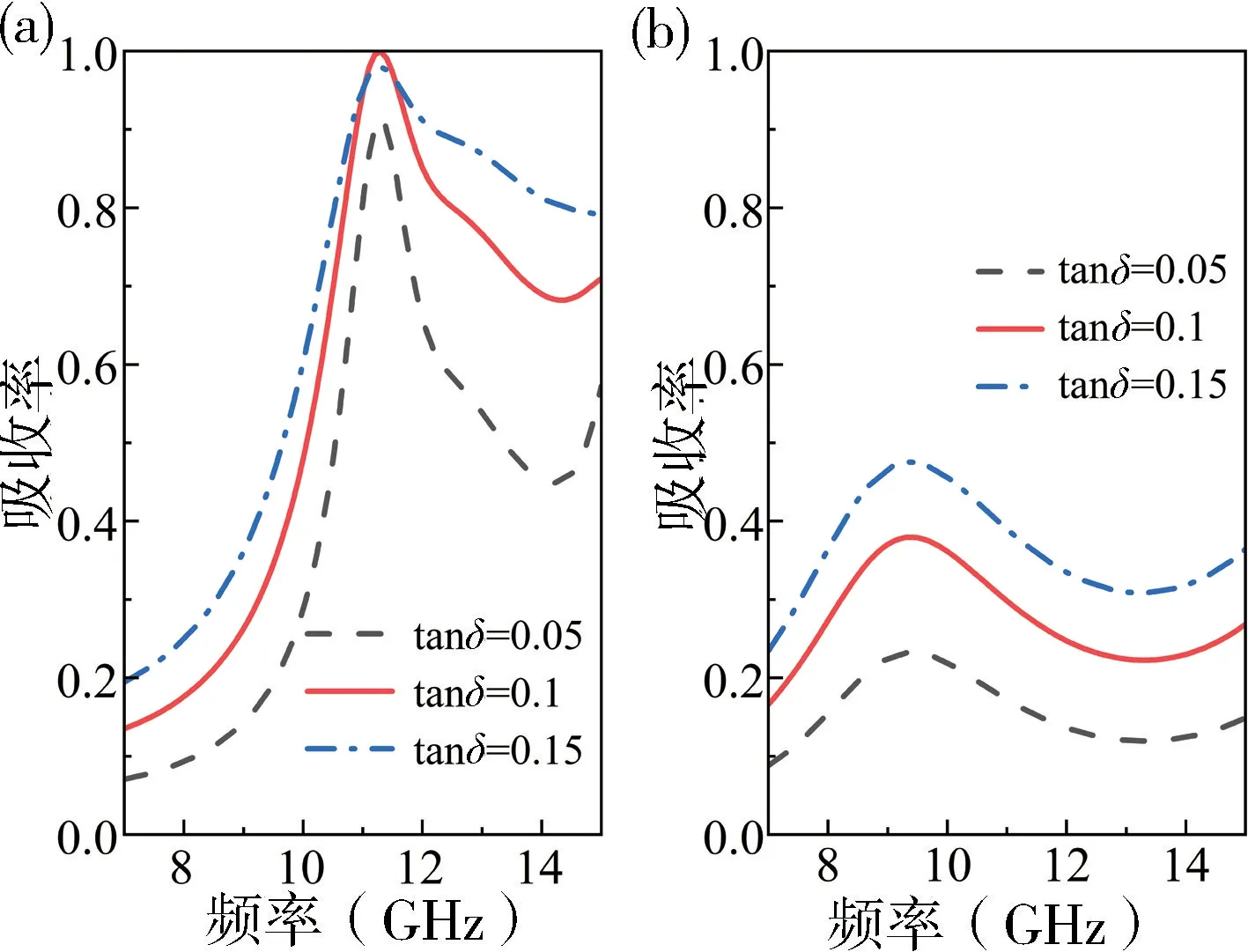
圖3 (a)圓孔陣列超表面和(b)介質平板的吸收率隨損耗角正切的變化Fig.3 The absorptivity of (a) circular hole array metasurface and (b) dielectric plate varies with the tangent of the dielectric loss angle

以上研究是5 mm 厚度介質板上分布周期性圓孔陣列實現完美吸收的情況,對于相同材料參數不同厚度的介質板,通過優化圓孔陣列的周期和直徑,也能在其他頻段實現完美吸收,從而實現完美吸收的連續可調諧性。圖4 為厚度從3 mm 變化到7 mm 時完美吸收的圓孔直徑D與諧振頻率處的波長λ0的關系曲線。當厚度為3 mm,周期和直徑分別優化為9.6 mm 和8 mm 時,在18.8 GHz(波長為16 mm)處實現完美吸收;當厚度為6 mm,周期和直徑分別優化為19.2 mm和16 mm 時,在9.4 GHz(波長為32 mm)處實現完美吸收。因此在各自諧振頻率處,圓孔直徑與諧振波長的比值基本符合D/λ0=0.5 的關系,與Yang 等的文章報道結果[23]一致。

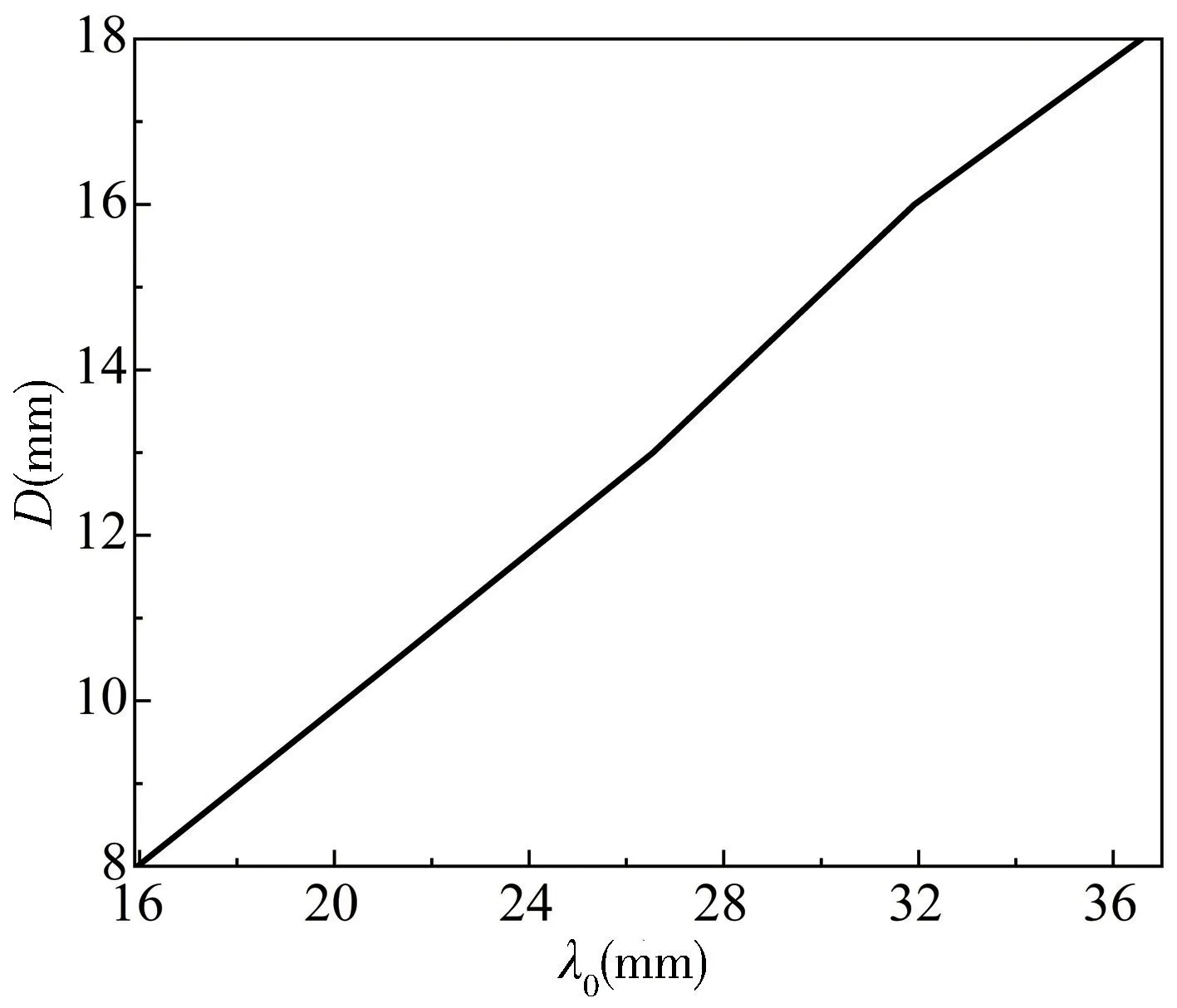
圖4 不同厚度超表面實現完美吸收時直徑與諧振波長的關系Fig.4 Diameter versus resonant wavelength for perfect absorption at different thicknesses of metasurface

上述研究都是基于電磁波的垂直入射(入射角為0°),對于斜入射的情況,研究結果如圖5 所示。設置材料的介質損耗角正切值為0.1、超表面的周期為16 mm,通過優化圓孔直徑和厚度,實現對超表面的完美吸收。由于超表面的單元結構具有中心對稱性,所以只考慮入射角在0°～90°范圍內的變化。當入射角為30°時,圓孔直徑和厚度分別調整為14.4 mm 和4 mm,超表面的吸收率最大(98.1%),實現近完美吸收,如圖5(a)所示。圖5(b)和(c)給出了入射角分別為45°和60°的超表面最佳吸收情況。從圖中可以看出,隨入射角增大,吸收率將逐漸減小。

圖5 入射角分別為(a)30°、(b)45°和(c)60°的吸收譜Fig.5 Absorption spectra with incidence angles of (a) 30°,(b) 45° and (c) 60°

2 實驗案例

從以上電磁仿真研究結果可知,全介質超表面完美吸收需要兩個基本條件,即超表面結構產生的電諧振模態和磁諧振模態發生簡并且兩個模態都處于臨界耦合狀態。然而,對于由同一種材料組分構成的介質基板而言,其材料的損耗難以與形成的諧振結構的輻射損耗剛好達到臨界耦合。因此,本實驗采用損耗極小的聚四氟乙烯陶瓷復合材料和損耗較大的磁性復合材料吸波片實現完美吸收。其中,聚四氟乙烯陶瓷復合材料的相對介電常數經測試為10,磁性復合材料吸波片由綿陽西磁科技有限公司生產,其相對介電常數和磁導率的測試結果如圖6(a)所示。磁性復合材料吸波片覆蓋在聚四氟乙烯陶瓷復合材料基板上得到的雙層圓孔超表面單元結構如圖6(b)所示,通過調節這兩種材料的厚度,使雙層基板組合達到簡并臨界耦合,進而實現完美吸收。

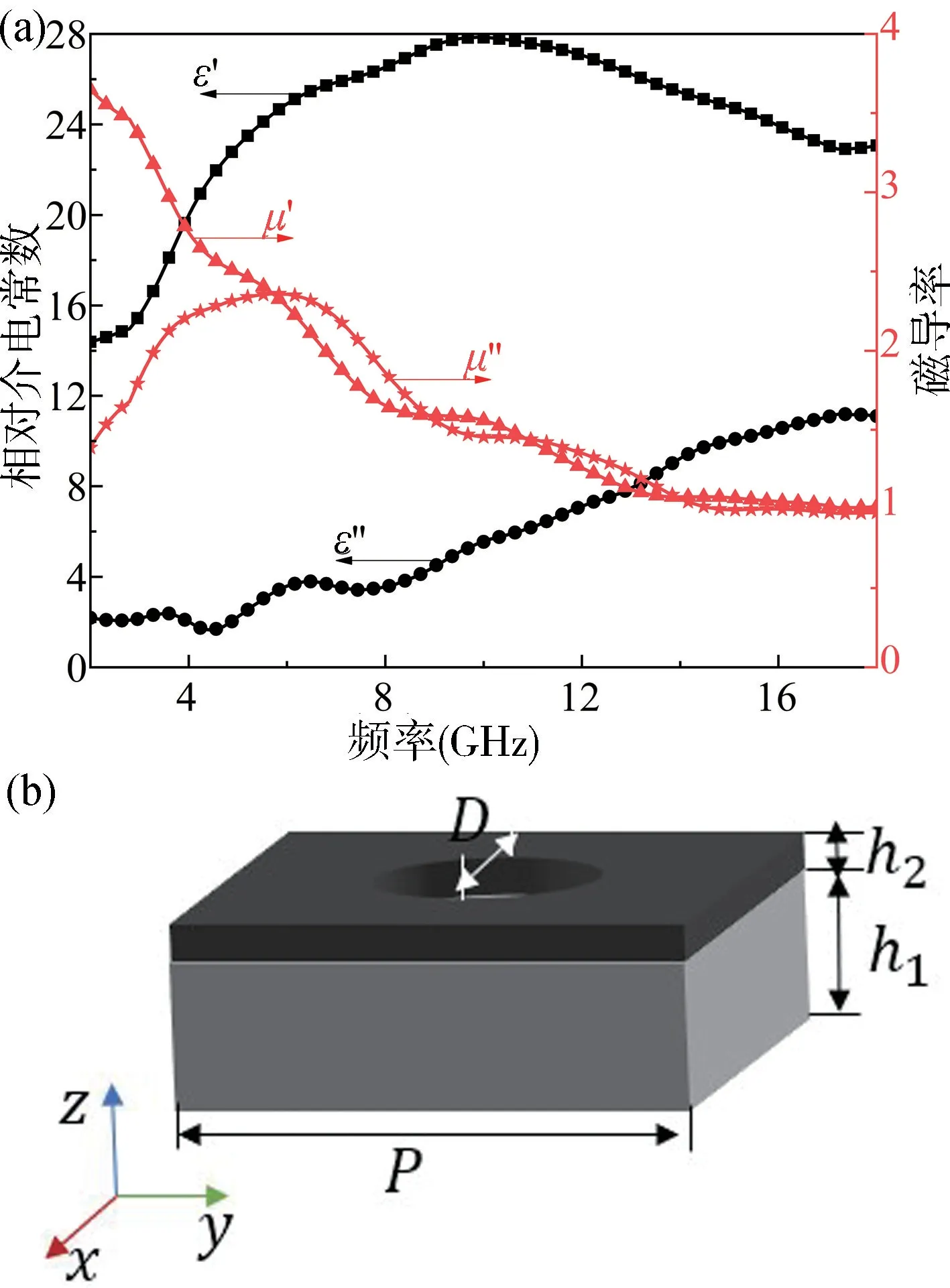
圖6 (a)磁性復合材料吸波片的材料參數、介電常數的實部( ε′)和虛部( ε″)以及磁導率的實部( μ′)和虛部( μ″)隨頻率變化的曲線;(b)全介質超表面吸收器的單元結構,由上到下第一層為磁性吸波材料,第二層為聚四氟乙烯陶瓷復合材料Fig.6 (a) Material parameters of the magnetic composite absorber,the real ( ε′) and imaginary ( ε″) parts of the permittivity and the real ( μ′) and imaginary ( μ″) parts of the permeability as a function of frequency;(b) Unit structure of the all-dielectric metasurface absorber,from top to bottom the first layer is the magnetic absorbing material and the second layer is the Teflon ceramic composite

確定周期P=20 mm,圓孔直徑D=17 mm,分別調節聚四氟乙烯陶瓷復合材料的厚度h1和磁性復合材料吸波片的厚度h2。考慮到雙層圓孔結構的非對稱性,需研究電磁波在不同端口入射時對吸收性能的影響。首先,考慮電磁波沿z軸方向入射(正入射)時的吸收情況: 圖7(a)為磁性復合材料吸波片的厚度設置為1 mm,聚四氟乙烯陶瓷復合材料的厚度從3 mm 變化到5 mm 時的吸收譜。從圖中可以看出,當h1=4 mm 時,超表面在10.3 GHz 處實現了完美吸收(99.6%);圖7(b)為聚四氟乙烯陶瓷復合材料的厚度h1=4 mm,磁性復合材料吸波片的厚度從0.5 mm 變化到1.5 mm 時吸收曲線,從圖中可以清楚地看出,當h2=1 mm 時超表面在10.3 GHz 處實現了完美吸收(99.6%)。所以,對于圓孔直徑和圓孔周期固定的情況,可以通過調節聚四氟乙烯陶瓷復合材料和磁性復合材料吸波片的厚度實現雙層介質結構的完美吸收。接著,考慮電磁波沿z軸負方向入射(反入射)時的吸收情況;圖7(c)為磁性復合材料吸波片厚度為1 mm,聚四氟乙烯陶瓷復合材料的厚度在3～5 mm 變化過程中的吸收譜;圖7(d)為聚四氟乙烯陶瓷復合材料的厚度為4 mm,磁性復合材料吸波片的厚度在0.5～1.5 mm 變化過程中的吸收譜。從這兩幅圖中可以看出,反入射時吸收率較低,所以僅僅通過調節聚四氟乙烯陶瓷復合材料和磁性復合材料吸波片的厚度無法實現完美吸收。

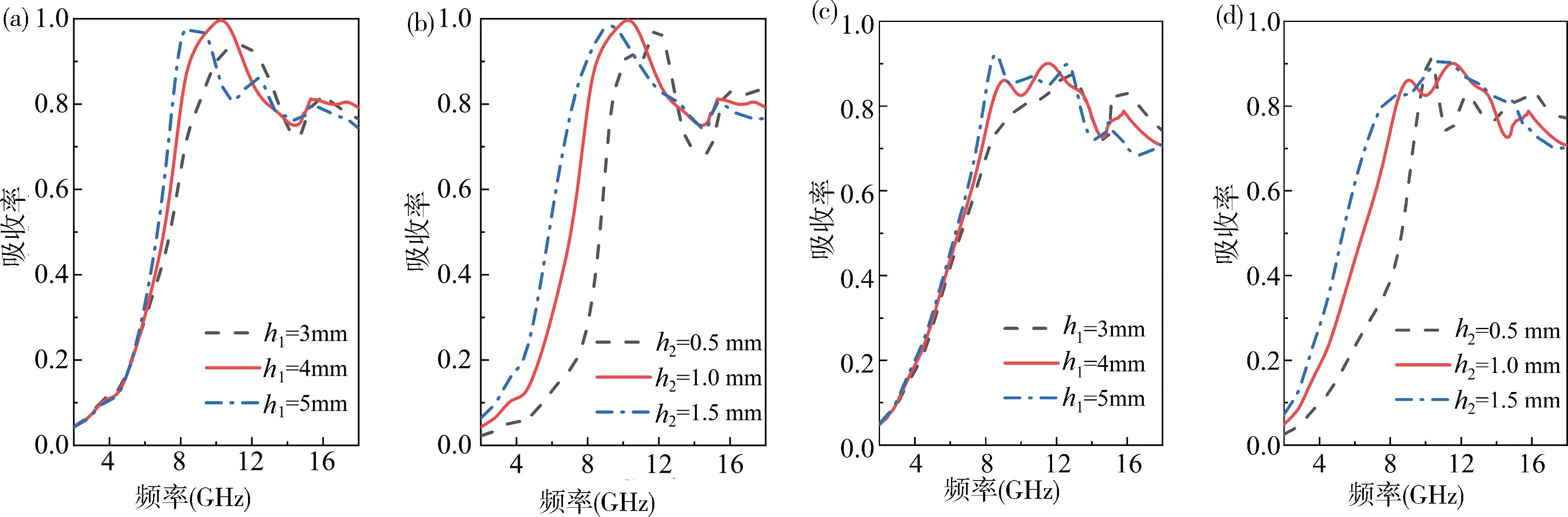
圖7 周期P=20 mm,圓孔直徑D=17 mm。電磁波正入射: (a) 磁性復合材料吸波片厚度為1 mm,聚四氟乙烯陶瓷復合材料厚度在3～4 mm 變化過程中的吸收譜;(b)聚四氟乙烯陶瓷復合材料厚度為4 mm,磁性復合材料吸波片厚度在0.5～1.5 mm 變化過程中的吸收譜;電磁波反入射: (c)磁性復合材料吸波片厚度為1 mm,聚四氟乙烯陶瓷復合材料厚度在3～4 mm 變化過程中的吸收譜;(d)聚四氟乙烯陶瓷復合材料厚度為4 mm,磁性復合材料吸波片厚度在0.5～1.5 mm 變化過程中的吸收譜Fig.7 Period P=20 mm,circular hole diameter D=17 mm.Electromagnetic wave forward incidence: (a) Absorption spectrum of magnetic composite absorbers with a thickness of 1 mm and teflon ceramic composite thickness varying from 3 mm to 4 mm;(b) Absorption spectrum of magnetic composite absorbers with a thickness of 4 mm and Teflon ceramic composite thickness varying from 0.5 mm to 1.5 mm;Electromagnetic wave back incidence: (c)Absorption spectrum of magnetic composite absorbers with a thickness of 1 mm and a thickness of teflon ceramic composite varying from 3 to 4 mm;(d) Absorption spectrum of teflon ceramic composite with a thickness of 4 mm and magnetic composite absorbers varying in thickness from 0.5 to 1.5 mm

圖8(a)為單元結構在xy平面10×10 陣列的實驗樣品,對該樣品進行的測試裝置如圖8(b)所示。在測試過程中,電磁波正入射的頻率范圍為6～18 GHz,測得的反射率、透射率和吸收率隨頻率變化的曲線如圖8(c)所示。從圖8(c)中可以看出,在9.68 GHz 處,吸收率的測量值達到了最大(92.4%),與仿真結果的差異主要是由于樣品的尺寸較小而未能使諧振頻率處入射波的透射率完全變為0 導致的。圖8(d)為電磁波反入射的情況下實驗和仿真結果,造成二者差異的原因與上述基本相同。因此,從兩個實驗結果來看,圓孔陣列全介質超表面具有接近完美吸收的吸波性能。

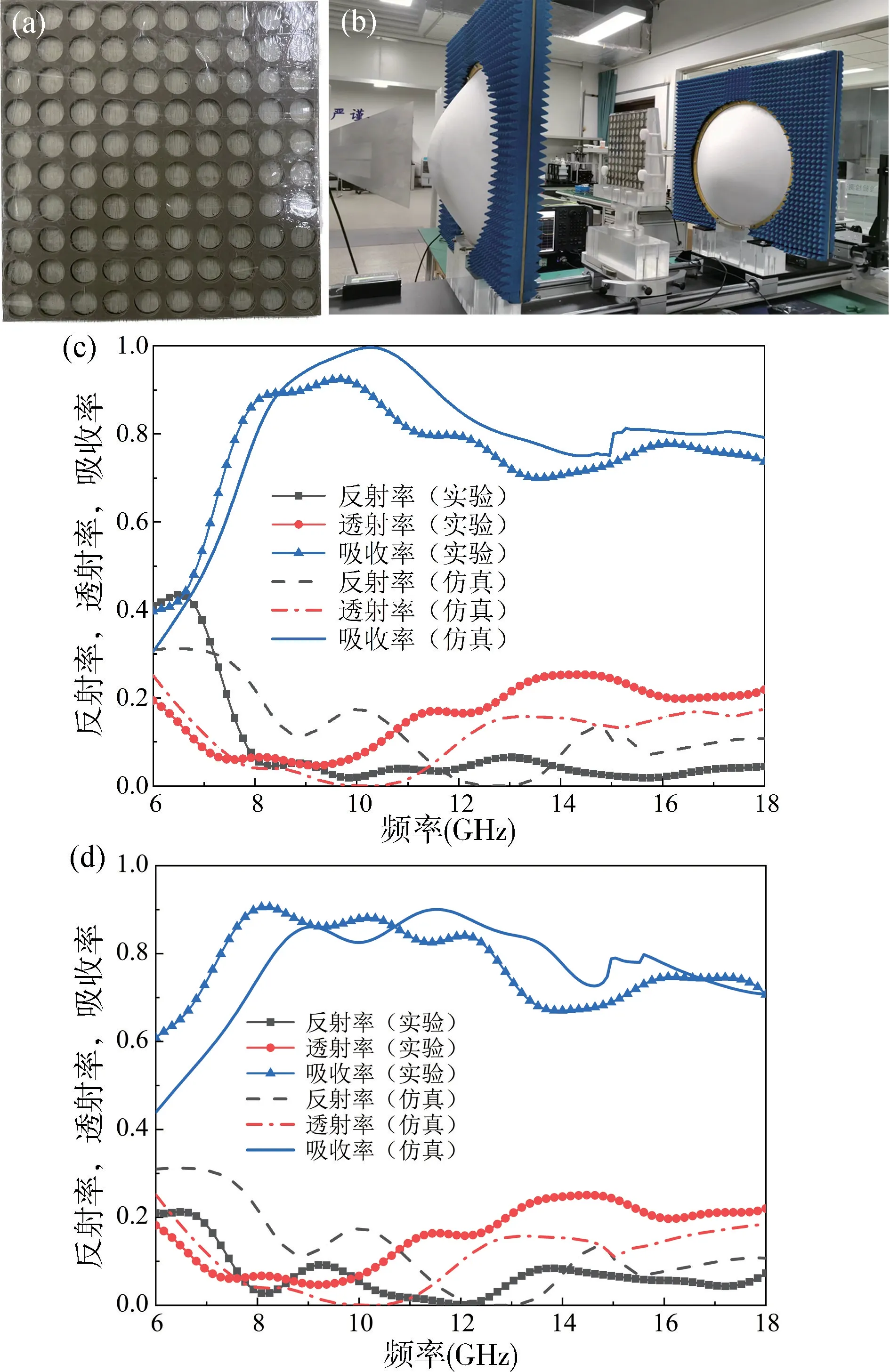
圖8 (a)全介質超表面樣品;(b)實驗測試裝置;電磁波(c)正入射和(d)反入射時吸收器的實驗和仿真結果Fig.8 (a) All-dielectric metasurface sample;(b) Experimental test equipment;Experimental and simulation results of absorber at(c) forward and (d) reverse incidence of electromagnetic wave

3 結論

本文提出了一種雙層圓孔陣列構建的全介質超表面完美吸收器。通過優化圓孔陣列幾何參數,使超表面中激發的電諧振和磁諧振簡并,再通過優化介質材料的損耗使材料損耗率等于輻射損耗率,進而實現超表面的完美吸收。采用厚度為1 mm 的磁性復合材料吸波片覆蓋在厚度為4 mm 的聚四氟乙烯陶瓷復合材料上的雙層介質結構,在其上排列周期為20 mm、直徑為17 mm 的圓孔陣列時,能夠在10.3 GHz 的頻率處實現完美吸收。實驗結果表明在9.68 GHz 處的吸收率為92.4%。仿真與實驗結果的差異是由于樣品的尺寸較小造成的。本文提出的雙層圓孔陣列全介質超表面具有吸收效率高、結構簡單、成本低等優點,有望在電磁隱身和屏蔽的應用中發揮重要應用。