云巴系統線路最小坡段長度參數的探討

王澤欣

(中鐵第五勘察設計院集團有限公司,北京 102600)

0 引言

云巴系統作為城市軌道交通中低運量制式的一員,具有諸多優勢。云巴工程投資低,可降低快速公共交通系統發展初期的投資門檻,在較小的財務風險下,提前實現交通供給;同時也可以最大程度上避免對城市地面交通及路權資源的占用;保證地面交通系統不受大的影響。舒適度作為城市軌道的一個重要的指標,云巴系統應重點考慮。由于列車通過變坡點時會產生附加力和附加加速度,設計較長的坡段有利列車平穩性。但實際工程中,會遇到諸多工程控制點,較長坡段對其適應性不強。故應綜合選取合適的坡段長度。

1 云巴簡介

云巴車輛采用橡膠車輪沿U型軌道梁上方行走的中小運量交通系統,其導向輪鑲嵌于軌道梁的內側;主要采用高架敷設,建設周期短,成本低,使用橡膠輪胎驅動及導向,線路半徑小,坡度大,地形適應性好,運營噪聲低、振動小,造價相對較低。參照貴州省住建廳頒布的DBJ52/T 092—2019膠輪有軌電車交通系統設計規范[1],云巴系統車輛的主要技術參數如表1所示。

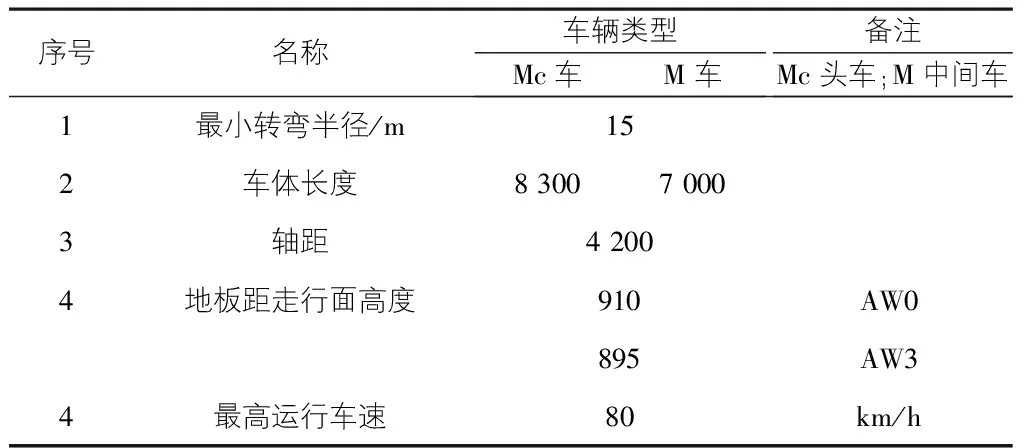
表1 云巴車輛主要技術參數表

2 列車舒適度分析

列車舒適度主要與列車未被平衡水平向的離心加速度as和垂向離心加速度az有關,本文主要分析垂向離心加速度az。

2.1 坡度代數差

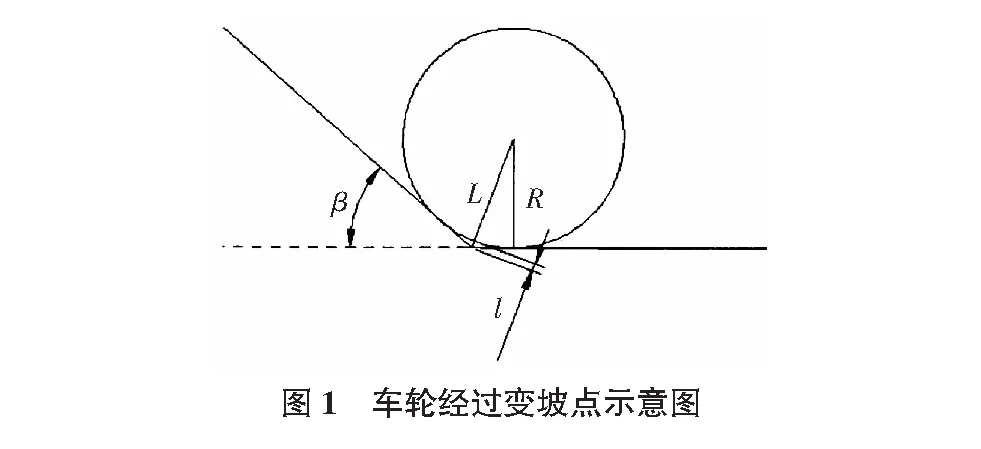
列車經過線路縱斷面的變坡點處(見圖1),會產生瞬時的沖擊加速度,影響旅客的乘車舒適度。為分析不設置豎曲線對導軌式有軌電車動力學響應的影響,利用動力學軟件進行以下仿真[2-4]。

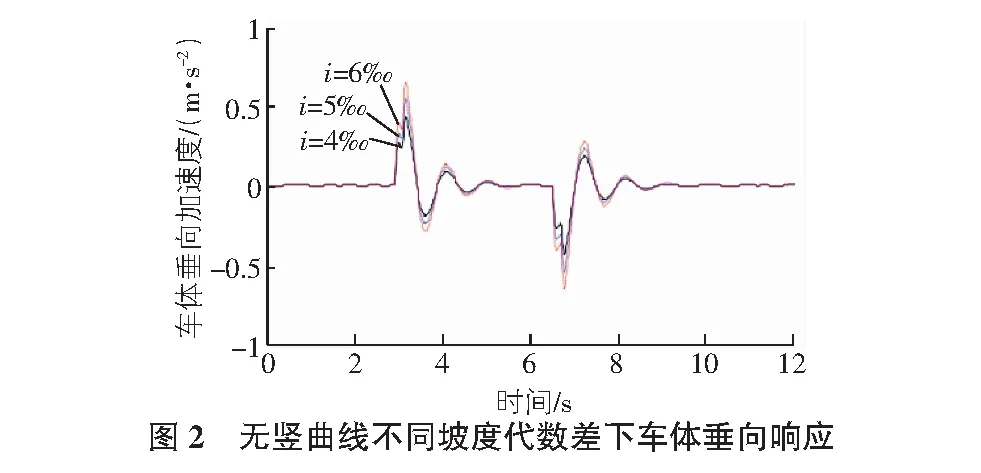
當坡道不設置豎曲線時,車輛通過變坡點時會產生一定的沖擊,坡度代數差越大,則車體垂向振動響應越劇烈。當坡度為4‰時,車體垂向響應幅值為0.45 m/s2,滿足舒適度要求;坡度為5‰時,車體垂向響應幅值為0.54 m/s2,超過舒適度允許值(見圖2)。

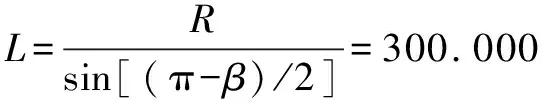
因此,兩相鄰坡段的坡度代數差不小于5‰時,應設圓曲線型的豎曲線連接。

2.2 豎曲線半徑

參考地鐵、單軌、公路等交通設計規范[5-7],豎曲線線型宜采用圓曲線形。列車在通過豎曲線時,產生的豎直向上或者向下的離心加速度不應大于旅客舒適度要求的加速度允許值。由此限制豎曲線半徑的計算公式為:

其中,V為設計車速,km/h;Rz為豎曲線半徑,m;az為垂向離心加速度允許值,m/s2。

各制式豎曲線上的垂向離心加速度允許值如表2所示。

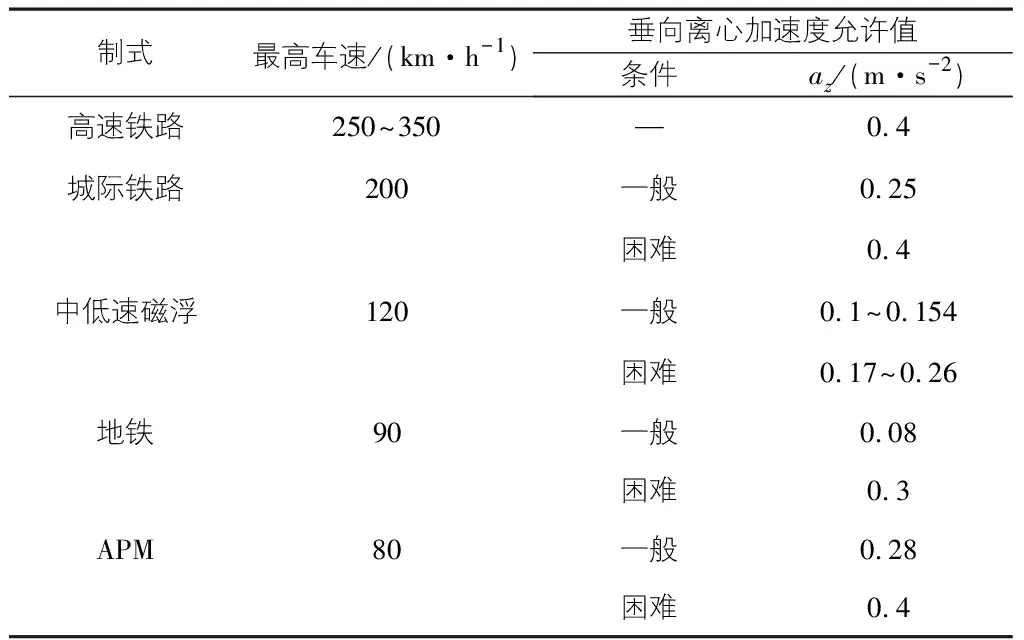
表2 各制式豎曲線上的垂向離心加速度允許值

結合行業經驗,建議云巴系統車輛垂向離心加速度允許值az一般條件下取值0.28 m/s2,困難取值為0.4 m/s2。

分析豎曲線半徑對車輛動力學響應的影響,仿真計算參數:行車速度80 km/h,坡度6%,豎曲線半徑分別取500 m,1 000 m,2 000 m,不考慮軌道隨機不平順。分別計算不同半徑對車體垂向振動加速度和輪軌力的影響,結果如圖3,圖4所示[8-9]。

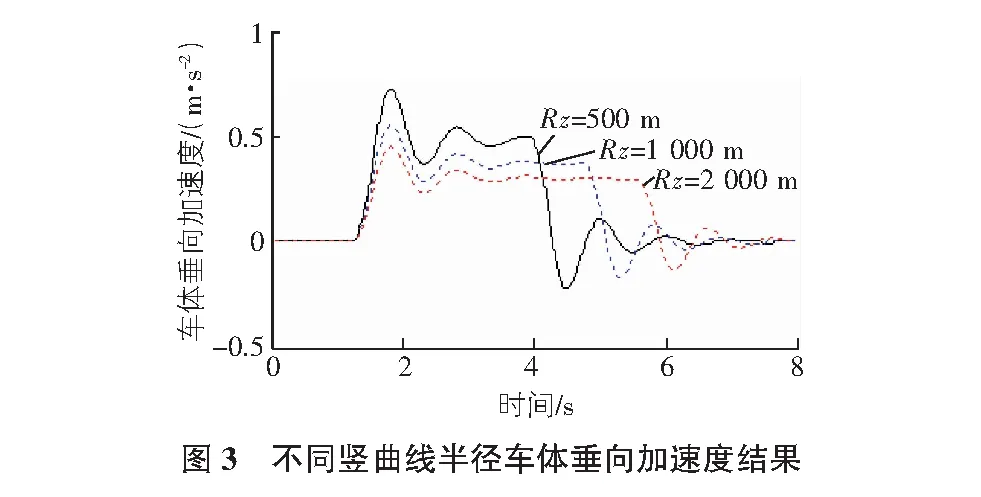
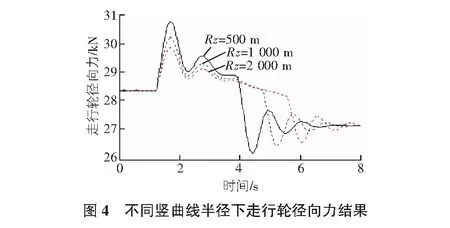
1)隨著豎曲線的半徑增大,車體的垂向加速度幅值逐漸減小,從舒適度評價指標來看,增大豎曲線半徑,舒適度指標逐漸減小,因此選取較大半徑的圓曲線均有利于行車的安全性和舒適性。

2)計算取整得,云巴系統線半徑一般取2 000 m,困難條件下取1 000 m(見表3)。

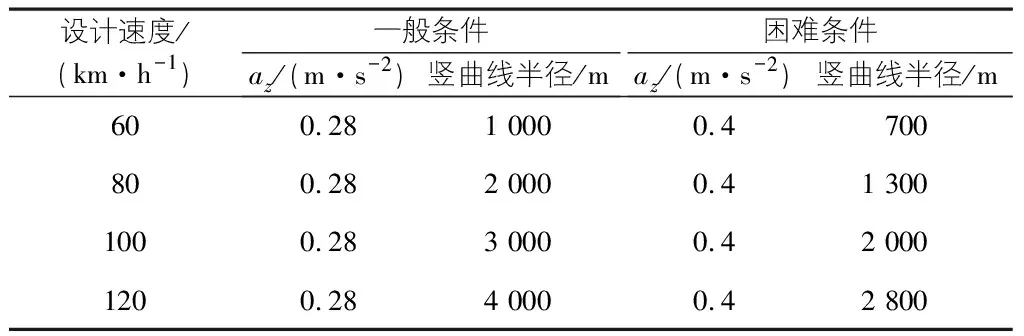
表3 不同工況下豎曲線半徑限值

2.3 豎曲線最小長度

豎曲線的最小長度與相鄰豎曲線間夾直線長度的確定方法一致,關鍵性因素為行車速度和車體垂向振動的衰減時間豎曲線長度與夾坡段長度確定原則一樣,主要有兩個原則:一是舒適度,二是安全性。以夾坡段為例,其中舒適度主要考慮車輛在前一個豎曲線產生的振動衰減后再進入第二個曲線,不致兩個曲線的振動疊加,按照這一要求,夾坡段的長度就是振動衰減所需的距離。安全性為輪軌的幾何關系,保證車輛任何時候都不跨越兩種線型,按照這一要求,夾坡段長度原則上不小于一節車輛長度。故豎曲公式為:

其中,Vmax為最高運行速度,km/h;Ls為豎曲線長度,m;n為振動衰減周期次數;Tz為垂直振動周期,s。

其中,參數n和Tz與車輛的結構和二系懸掛的特性有關。根據云巴系統列車懸掛參數計算出其車體垂向振動(沉浮振動和點頭振動)頻率在1.0 Hz～1.2 Hz左右,振動周期約為Tz=0.8 s～1 s,且振動響應的衰減在兩個周期內基本完成,即n=2。因此以云巴系統列車兩個垂向振動周期的運行距離定義夾坡段的最小長度,換算為長度即為0.5Vmax。同時為了避免一節車同時跨越兩個線型,要求最小夾坡段長度不應小于一節車長度,即15 m。

根據以上分析,建議夾坡段直線的最小長度為一般地段40 m,困難地段15 m。

2.4 豎曲線最大切線長分析

豎曲線切線長可由下列公式可得:

豎曲線切線長和坡度代數差與豎曲線半徑的大小有關。列車經過變坡點的時候產生垂向力和垂向加速度,通過豎曲線連接相鄰坡段能夠有效減緩車輛振動和垂向加速度。然而當坡度代數差太大時(例如反向大坡度坡段),列車交替加速減速,影響列車行駛平穩性與乘客舒適性。綜合考慮乘客舒適性、降低養護維修和運營費用等方面,應當對坡度代數差的最大值做限制。參照普速鐵路、跨坐式單軌、中低速磁浮等制式的常規做法,建議Δimax=imax=80‰。則由上式可得,一般情況下,TSHmax=80 m;困難情況下,TSHmax=40 m。

3 最小坡段長度

3.1 最小坡段長度分析

若采用較短坡段長度,工程上,能夠更好適應地形;但會降低列車運行平穩性,降低乘客舒適度。故,坡段長度既要考慮降低工程量又要滿足列車平穩運行的要求[10]。

坡段長度由相鄰豎曲線的切線長度和夾坡段直線長度構成,如圖5所示。

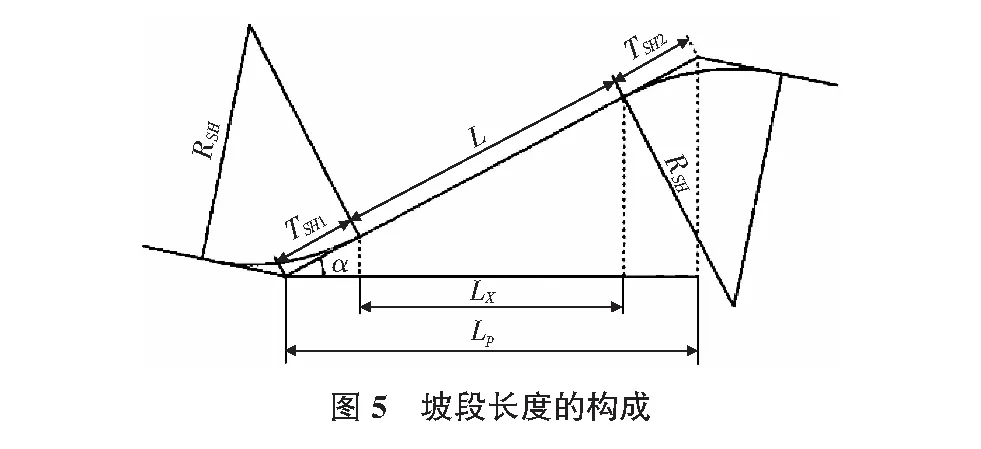
由于tanα≤imax≈80‰,cosα≥0.996 8,

得:(L+TSH1+TSH2)×cosα≈Lx+TSH1+TSH2,Lx=L×cosα≈L。

其中,LP為坡段長度;TSH1為前一豎曲線切線長;TSH2為后一豎曲線切線長;L為夾坡面長度;Lx為夾坡段長度;α為該坡段坡度角;i為該坡段坡度。計算可得L一般=200 m;L困難=100 m。

3.2 列車不同時跨兩個變坡點

云巴系統列車線路的最小坡段長度應滿足其不小于云巴列車長度的要求,以避免變坡點附加力的疊加影響和附加力的頻繁變化,保證行車的平穩。

云巴采用全動車設計,編組靈活,可根據不同的運量需求選擇2節～4節車輛自由編組,每節車廂2個單軸轉向架,連接的兩節車廂之間設有貫通道和車鉤。其中Mc車長度為8 300 mm,M車長度為7 000 mm(見圖6)[11]。

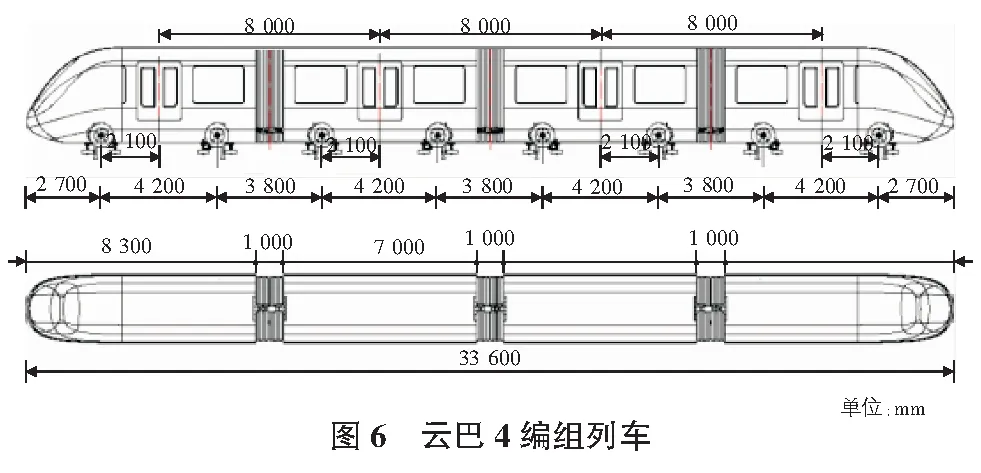
考慮到遠期4輛編組的目標,建議云巴線路最小坡段長度不小于33.6 m。

3.3 最小坡段長度的取值

綜合分析,豎曲線的切線長度與夾坡段的直線長度確定的最小坡段長度;列車長度(不同時跨越兩個變坡點)所確定的最小坡段長度,得到云巴系統線路的最小坡度長度:一般情況為200 m,困難情況為100 m。

4 結語

本文結合跨坐式單軌等制式的線路最小坡段長度的確定方法與云巴系統自身的技術特點,確定了云巴系統線路的最小坡段長度。本文所確定的一般200 m,困難100 m的最小坡段長度參數已在武漢黃陂云巴可行性研究中得到應用,得到專家認可。而現運營的璧山云巴1號線由于采用參數偏小,車輛經過時突變振動明顯。全國運營的云巴的線路里程較短,缺乏一定的實踐經驗,最小坡段長度的取值還需在以后實踐中進一步驗證和完善。