結合極化自注意力機制的空間目標位姿估計

竇凱云,樊永生,王 濤

1.中北大學大數據學院,太原 030051 2.中北大學電氣與控制工程學院,太原 030051

0 引言

近年來,人類太空活動日漸頻繁,在軌航天器數量與日俱增。傳統航天器造價昂貴卻只能一次性使用,因而在軌服務出現,為太空中的航天器提供部件維修、更換等服務[1]。通過目標飛行器相對于服務飛行器的位姿估計推斷目標的運動狀態,是空間在軌服務的基礎和關鍵技術之一。位姿估計是估計相機坐標系下目標的位置和姿態。傳統的目標位姿估計方法包括基于特征點的方法、基于模板的方法和基于點云的方法,整體是通過從圖像中提取特征后建立二維像素點與三維位置點的對應關系來計算位姿[2]。基于特征的方法是通過提取圖像像素中的局部特征與三維模型上的特征進行匹配,建立2D-3D對應(典型的如PnP算法),從而得到位姿信息。它對于物體之間的遮擋有很好的處理效果,但需要豐富的紋理來計算局部特征。基于模板的方法是通過模板匹配得到物體的位姿信息,對無紋理對象效果很好,但對光照和遮擋都很敏感。基于點云的方法處理對象是點云數據,通過求解3D-3D特征點的對應關系來獲取位姿,對光照敏感,因此不適用于室外場景。

隨著近年來深度學習的發展,通過卷積神經網絡[3]從圖像中學習目標的位姿特征提高了目標位姿估計的速度和準確度[4]。Yu等[5]提出的PoseCNN網絡可以從RGB圖像中直接回歸得到6D相機姿態,其將VGG網絡提取的圖像特征輸入到分割、平移、旋轉3個網絡分支。其中,分割分支得到每個像素的類別標簽;平移分支通過投票機制估計位置信息;旋轉分支在RoI Pooling后通過全連接層回歸到四元數得到目標的姿態信息。Do等[6]提出的Deep-6D pose框架同樣采取了直接回歸的方式,與PoseCNN不同,它的位置分支與姿態分支全部使用全連接層直接回歸的方式,并且創新性的采取了李代數表示旋轉信息。除了直接回歸以外,Rad等[7]提出的BB8將CNN網絡獲取的物體三維邊界的頂點投影到二維圖像中,通過PnP算法計算位姿。Pix2Pose[8]和PVnet[9]等方法同樣是獲取圖像的關鍵點后建立2D-3D映射關系,通過PnP方法得到6D位姿。

相比采用關鍵點進行預測,使用PnP算法計算位姿,直接回歸能夠以端對端的方式輸出位姿。本文與直接回歸的位姿估計方法如Deep-6D pose相比,引入Polarized Self-Attention注意力機制嵌入到殘差網絡ResNet-50[10]中,利用其獨特的極化濾波和HDR機制,對圖像中空間目標的空間信息通過加權進行了增強,提高姿態估計的精準度。同時借鑒PoseCNN的方法解耦位姿,用2個分支分別獲取圖像的位置和姿態信息,但不同于PoseCNN。PoseCNN使用2個分支用于姿態回歸,1個用于位置回歸。在姿態信息回歸分支上,對姿態信息進行軟分配編碼,相比于直接回歸能有效減少姿態誤差。最后在URSO數據集上進行了實驗驗證,實現了空間目標的端對端位姿估計。

1 網絡結構設計

空間目標的位姿估計包括位置估計和姿態估計,本文采用端對端的回歸法從圖像數據中學習空間目標的位姿映射關系以得到位姿數據。

1.1 網絡框架

對于給定的輸入圖像,姿態估計的任務是獲取目標從物體坐標系到相機坐標系的變換,包括三維平移和三維旋轉。由于兩者有著不同的度量單位,分別為米和度,因此解耦為2個網絡分支分別計算。如圖1所示,整體網絡包括3個階段:

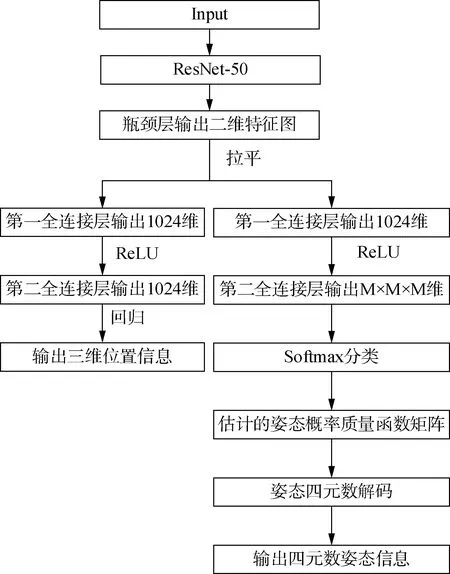
圖1 網絡結構圖

1)主干網絡。用殘差網絡ResNet-50提取圖像的深層特征。由于空間目標位姿估計需要深度學習網絡具備較強的空間位置提取能力,將Polarized Self-Attention注意力機制模塊嵌入殘差塊中,利用其獨特的極化濾波和HDR機制,對圖像中空間目標的顯著特征信息通過加權進行了增強。

2)嵌入網絡。將主干網絡輸出的二維特征圖輸入到可調節通道數的3×3卷積核進行二維卷積,步長為2,從而降低輸出維度,進行降維卷積處理,最終將特征圖經過拉平成一維數組,為后面全連接層的運算極大地減少了參數量,從而降低了訓練時間。

3)分支網絡。通過前兩階段生成的圖像特征通過2個分支分別輸出位置信息和姿態信息。其中,采取了兩層全連接層結構以直接回歸方式輸出三維信息。第一個全連接層用于將拉平后的特征圖信息再進行降維操作,壓縮至1024個維度,經過ReLU激活函數后,再將該層輸出數據輸入到下一個全連接層,最終輸出為三維數據,直接對應所求的三維坐標信息x,y和z。

姿態分支基于軟分配編碼實現,輸出四元數的姿態信息[11]。其中的核心思想是將姿態四元數按照高斯分布模型進行編碼,轉換為姿態離散空間中的概率質量函數值,因此該分支結構針對概率質量函數進行學習。最終可將網絡輸出的包含概率質量函數的三維矩陣解碼,得到估計出的位姿四元數值。

1.2 注意力機制

在空間目標的位姿估計中,空間位置提取能力對結果精準度有很大影響。對于包含空間目標的整張圖像,空間目標只占其中有限的一部分,其余的是太空背景和地球背景,占據了不小的面積。在深度學習過程中,這些背景信息由于參與了卷積等計算,產生了冗余信息,對空間目標的識別、定位和位姿估計均產生了干擾。因此,在深度學習過程中,針對性地提高空間信息的權重,降低不必要的干擾至關重要。為了實現空間目標的精準位姿估計,減少背景信息的干擾,本文將PSA(Polarized Self-Attention)注意力機制模塊嵌入到殘差塊中以解決該問題。

Polarized Self-Attention[12]由南京理工大學和卡內基梅隆大學于2021年聯合提出,是一種基于像素級回歸的雙注意力機制。它有2個特點:

1)極化濾波:大多數的像素級回歸為了魯棒性和計算效率而輸出低分辨率的特征,高度非線性的物體邊緣部分會因此損失很多分辨率特征。而Proenca等[13]的研究表明,位姿估計對圖像分辨率的敏感度很高。PSA的極化濾波機制是使一個維度的特征完全折疊,其正交方向的維度保持高分辨率。如通道維度特征折疊,則空間維度特征保持高分辨率。因此,對于空間目標的位姿估計的精準度有一定的幫助。

2)High Dynamic Range(HDR):對注意力模塊中最小的特征張量進行softmax歸一化以擴寬注意力范圍,進行信息增強,然后使用sigmoid函數進行投影映射。

PSA注意力模塊分為通道分支和空間分支,在計算完成后通過串聯進行融合。

PSA注意力模塊中通道分支的權重計算公式為:

Ach(X)=FSG[Wz|θ1(Wv(X))×FSM(σ2(Wq(X)))]

(1)

其中:Ach(X)∈RC×q×1,FSM表示softmax函數,FSG表示sigmoid函數,W表示不同的卷積操作,σ表示不同的降維操作,×表示矩陣點積運算。

通道分支先通過卷積操作Wv把通道數壓縮為一半,然后將其由二維特征圖降為一維,與壓縮全部通道的空間特征信息點積后,通過卷積Wz恢復通道數,最后經Sigmoid歸一化,把不同通道的權重加權到原來的特征上。另外,壓縮全部通道的空間信息還通過FSM函數進行了一次信息增強。

空間分支的權重計算公式為:

Asp(X)=FSG[σ3(FSM(σ1(FGP(Wq(X))))×

σ2(Wv(X)))]

(2)

其中:Asp(X)∈R1×H×W,Wv和Wq為卷積操作,σ1和σ2為降維操作,σ3為升維操作,FSG、FSM、FGP分別為sigmoid函數、softmax函數和全局池化。

空間分支與通道分支不同之處有2點:1)壓縮全部空間的通道信息,經過了卷積、全局池化、降維和softmax函數回歸;2)點積后沒有再一次的卷積操作,而是直接通過σ3恢復維度。

可見,PSA同時在空間和通道維度上保持了高分辨率,并且利用softmax對瓶頸張量進行了非線性激活。調整權重,即賦予重要特征信息更大權重,有助于增強圖像空間通道的顯著特征,更精準地定位空間目標在圖像中的位置。

因此,本節在主干網絡ResNet-50的殘差塊的BN層前加入PSA注意力機制模塊,使網絡更好地注意到圖像中空間目標的空間信息,同時盡可能減少圖像復雜背景的干擾。

1.3 軟分配編碼

姿態信息進行軟分配編碼[13]:首先為每個姿態角劃分24個區間,進而可以得到13824個姿態信息離散點,并可以近似地一一對應空間中任意一個姿態旋轉矩陣,用集合Q={b1,…,bN}來表示。其中,bi為用四元數形式表示的第i個姿態。然后對每個姿態信息bi按照下式進行軟分配編碼:

(3)

其中:K(x,y)為核函數,利用歸一化的姿態軸角偏差表示2個四元數x和y之間的相對誤差為:

(4)

(5)

其中:方差σ2表示量化誤差;Δ/M表示量化步驟;Δ為平滑項;M為三個姿態角各自劃分的區間數目。

對網絡輸出的概率質量函數進行解碼,即可得到估計的位姿四元數。網絡輸出的概率質量函數可用集合{w1,…,wN}表示。然后估計出的四元數為:

(6)

其中:N為姿態離散空間的離散點數目。

另外,在回歸的過程中,使用如下的損失函數來保證四元數的歸一化:

(7)

如圖1中右下的姿態分支網絡結構所示。同樣的,姿態分類分支與位置回歸分支的第1層結構仍然大體相同,為全連接層,區別在于第2全連接層之后的部分。第2層所輸出的維度為M×M×M維的,經過ReLU激活函數以及softmax分類,從而得到估計出的M×M×M維概率質量函數矩陣,到此網絡完成訓練部分。接下來是解碼該矩陣,進而得到輸出的四元數姿態信息。

1.4 損失函數

由于位置分支和姿態分支采取不同的回歸方法,因此采取不同的損失函數。

位置分支使用相對誤差形式而不是歐式距離。這是由于空間目標數據集的z軸范圍是10 m到20 m,當目標的z軸距離偏大時,導致歐式距離即估計位置與實際位置的幾何距離非常大,從而在小批量訓練中加大了對遠距離目標圖像學習的位置損失函數的權重,最終使網絡對近距離目標位置的估計能力下降。位置損失函數定義如下:

(8)

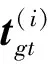
姿態信息的損失函數可由標簽信息編碼后的正態分布離散函數值與輸出信息的概率質量分布的交叉熵計算得到,交叉熵計算如下:

(9)

其中:x為離散空間中的一個四元數,Q={x1,…,xM3}為在離散空間上的四元數集合,p(x)為網絡對x的概率質量函數值,q(x)為由標簽值編碼后的概率質量函數對x的值。

2 實驗驗證

2.1 數據集

用于空間目標的識別、定位和位姿估計等的URSO數據集[13]基于虛幻引擎4(Unreal Engine 4)構建,用于渲染繞地球運行的航天器的高清圖像。USRO數據集是從近地球軌道高度在地球上隨機取5000個視點,空間目標隨機在攝像機觀察范圍10～20 m之間。其中,地球的自轉、相機方法和空間目標的姿態都是隨機生成的。數據集分為訓練集、測試集和驗證集,后兩者分別使用5000張圖像中的10%,圖像的分辨率大小為1280×960。圖2為部分展示。

圖2 URSO數據集(部分)

2.2 評價指標

評價指標是用來反映模型潛在的問題和評價模型性能優劣的定量指標。常規的是對各類物體位姿估計,本文是對一類物體即空間目標估計,因此采用歐空局針對空間目標提出的一套位姿估計評價方法[14],分別計算位置和姿態誤差。

位置誤差的計算公式如下:

(10)

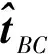
姿態誤差的計算公式如下:

(11)

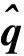
空間目標圖像的位姿估計的總誤差即為位置誤差和姿態誤差的總和,所有空間目標位姿估計的平均位姿誤差為總和除以圖像數量。

2.3 實驗結果

URSO數據集中包含復雜的太空背景和地球背景,有些航天器被淹沒在地球背景中。本文提出的空間目標深度學習位姿估計,即使在復雜的地球背景下仍能夠獲得魯棒的估計結果。基于URSO數據集測試本文算法,數據訓練180次,前100次學習率為0.001,后80次為0.0001。在相機坐標系下,根據2.2節評價指標,測試集的位置誤差為0.85 m,姿態誤差為9.7°。如圖3和圖4所示,隨著迭代次數增加,位置和姿態誤差趨于穩定。

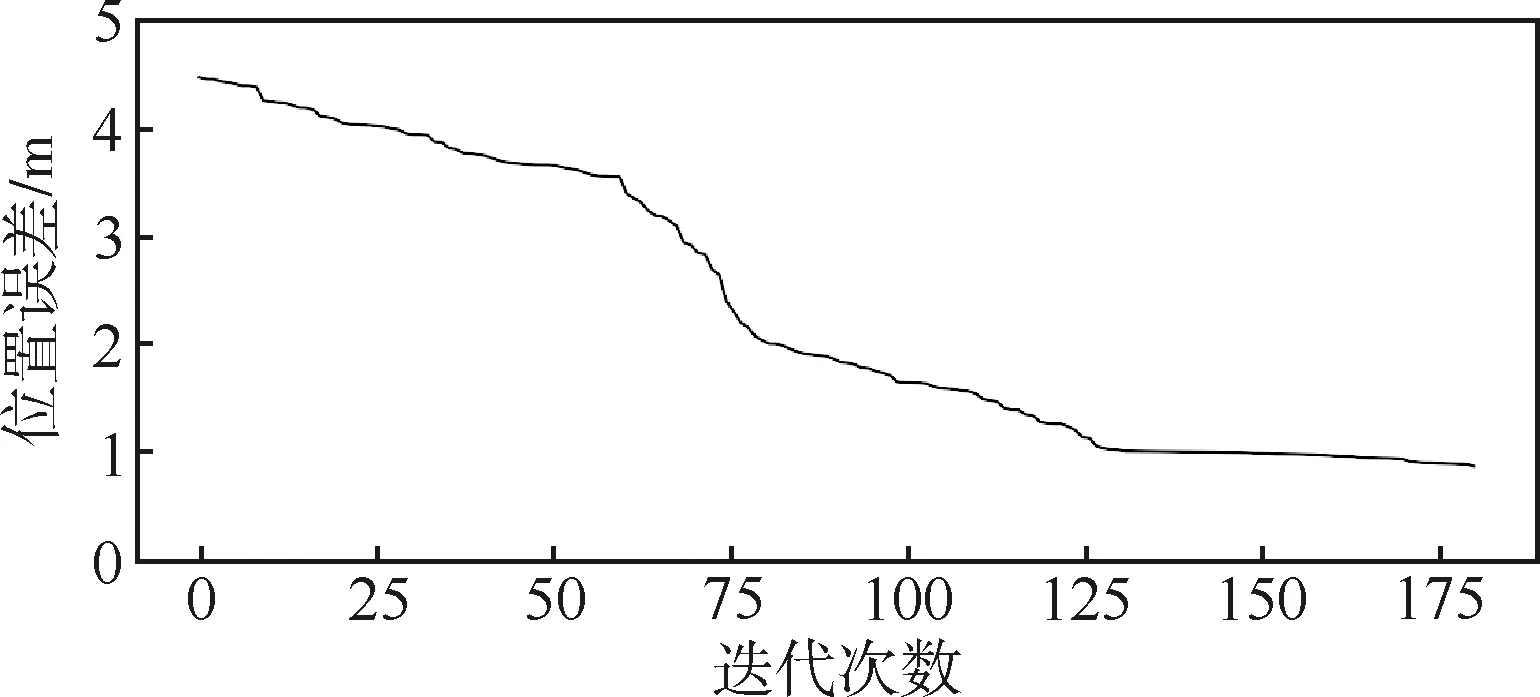
圖3 位置迭代誤差圖

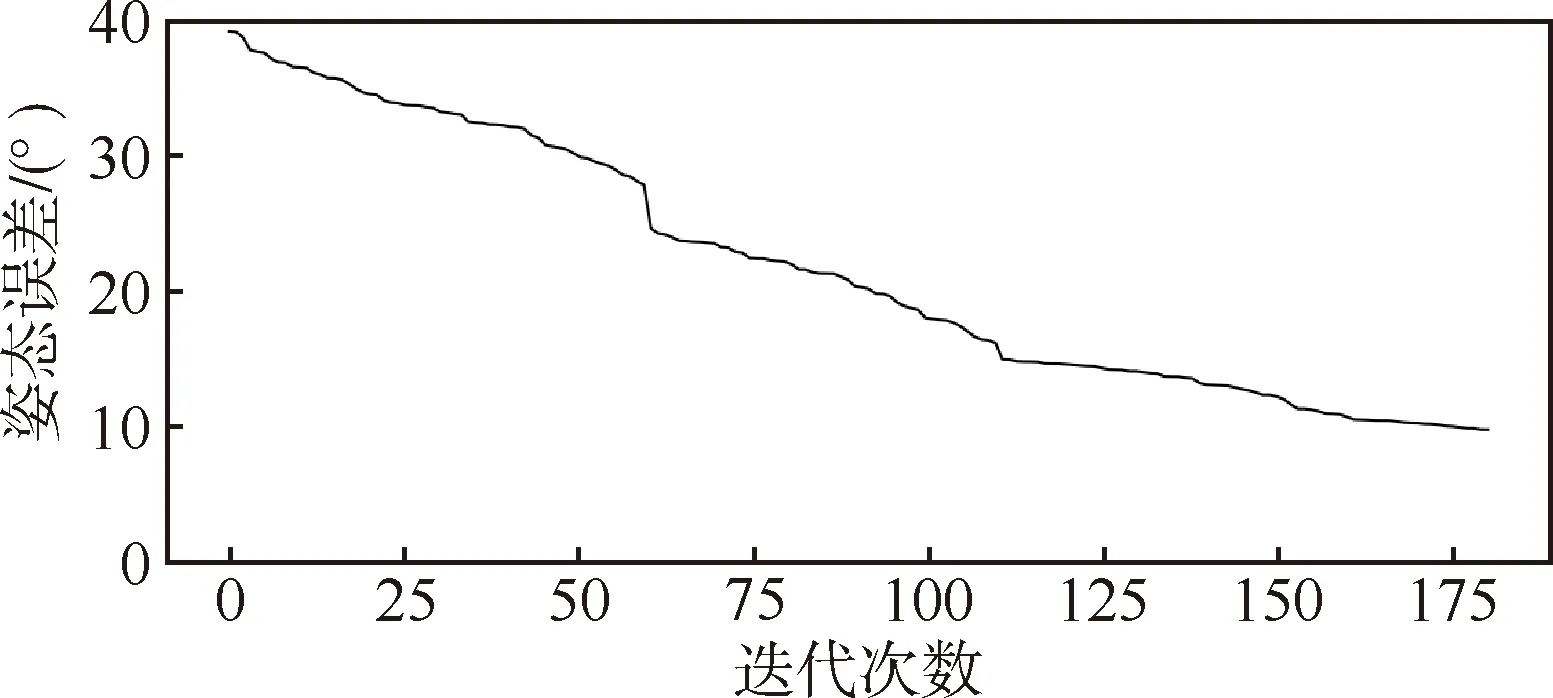
圖4 姿態迭代誤差圖

圖5給出了利用USRO數據集對本算法進行測試的可視化結果。在空間目標圖像中,為了進行可視化,將姿態信息的四元轉換為方向余弦矩陣后,結合相機參數映射到空間目標圖像中,紅、藍、綠三個箭頭分別表示航天器的俯仰角、滾轉角和偏航角,而三個箭頭的交匯處即為空間目標的位置。

圖5 基于URSO數據集的測試結果

圖5中的空間目標圖像在對小數點后3位四舍五入后,實際位置信息和姿態信息分別為[-0.601,3.455,17.287]和[0.147,0.408,0.452,0.779],而估計值分別為[-0.723,3.163,16.051]和[0.134,0.379,0.476,0.782],根據2.2提出的評價指標計算誤差,位置信息的平均絕對誤差約為0.95 m,姿態信息的角度誤差約為4.53°。其中,圖5(a)為位置可視化圖,兩個斑點分別表示真實位置和預測位置。圖5(b)展示了姿態信息在歐拉角的極坐標圖形式下的預測誤差,兩條虛線分別表示真實和預測角度信息。圖5(c)為姿態直觀可視化圖像。由此可見,本文所提算法具有一定的精準度。

為了驗證PSA注意力機制對于空間目標圖像位姿估計精度提升的有效性,在URSO數據集上進行了消融實驗,如表1所示。分析表1結果,對比可見,引入Polarized Self-Attention注意力機制可使得圖像位姿估計位置誤差精度從1.1 m提升到0.85 m,姿態誤差精度從10.9°提升到9.7°,表明引入注意力機制可以增加算法對圖像中重要特征信息的篩選能力,通過權重提升有效增強了算法在空間上的特征表達能力,有效提升了模型的估計精度。

表1 消融實驗結果

此外,為了充分評估本文設計的位姿估計算法,驗證其對空間目標位置和姿態估計的精準度,本文與直接回歸的空間目標位姿估計算法Deep-6DPose進行了對比。從表2可以得出,誤差估計和姿態估計的精度均有提升。

表2 不同算法模型在URSO數據集上的對比

3 結論

設計了一種基于深度卷積殘差網絡的方法用于空間目標的位姿估計,引入了Polarized Self-Attention注意力機制,實現了空間目標圖像對空間信息的加權,另外采取軟分配編碼取代姿態信息直接回歸,有效且有一定精準度地實現了空間目標端對端的位姿估計。