改進SO優化KELM的液體火箭發動機故障檢測*

王聞浩,許 亮

1.天津理工大學電氣工程與自動化學院,天津 300384 2.天津市復雜系統控制理論與應用重點實驗室,天津 300384

0 引言

液體火箭發動機作為液體火箭的核心,其運行工況的正常與否直接決定了火箭是否可以成功發射。液體火箭發動機屬于多學科、多領域的復雜耦合系統,當其運行于高溫高壓的極端環境下,極易出現難以預料的故障[1]。因此,對液體火箭發動機進行故障檢測顯得尤為重要。

分類算法是液體火箭發動機故障檢測的主要手段和方法。早期的故障檢測方法以神經網絡為主。王克昌[2]將BP神經網絡應用于火箭發動機故障診斷,指出在大量訓練樣本的支撐下,診斷結果的正確性可以得到保證。但其局限性在于,對于訓練樣本中不存在的故障情況,診斷結果的可信度大大降低。同時,當存在參數相近,而故障模式不同的樣本時,訓練過程較慢,且難以獲得理想的結果。王平等[3]采用神經網絡對滾動軸承故障包絡信號進行自動識別。從包絡信號的時域和頻域提取故障特征信息,作為神經網絡的輸入。結果表明,該神經網絡可以有效識別滾動軸承的各類運行故障。隨著分類算法的快速發展,火箭發動機故障檢測方法也更加多元。韓泉東等[4]將支持向量機應用于火箭發動機故障檢測。采用支持向量機對所有的故障類型設計一個分類器。根據所有分類器的輸出結果,對樣本故障類型進行判斷,仿真結果表明該方法可以有效識別故障。俞剛等[5]將支持向量機和卡爾曼濾波器結合。首先采用最小二乘支持向量機,對部件故障進行分類。最后由卡爾曼濾波器估計故障部件參數,從而進行故障檢測。

以上算法均可實現火箭發動機的故障檢測,但也存在一定的問題。BP神經網絡采用反向傳播學習算法,其網絡結構、初始權值和閾值對網絡訓練的影響很大。支持向量機分類的重要環節是懲罰因子和核函數參數的選取。對于這些問題,人們只能依靠已有的經驗,或將隨機參數帶入模型,通過觀察輸出結果選取最優值。為了解決這些問題,多數學者開始使用群體算法來優化分類模型。楊晉朝[6]采用遺傳算法優化BP神經網絡的權值和閾值,結果表明該模型可以有效避免網絡陷入局部最優。Xu等[7]采用量子遺傳算法優化BP神經網絡。許亮等[8]采用粒子群算法對小波神經網絡的權值和基函數參數進行了尋優,仿真結果表明所提出的模型訓練時間最少,且精度最高。陳占國等[9]建立了松鼠搜索算法優化支持向量機的故障檢測模型,實驗表明該模型具有較高的準確率。馬碩[10]采用改進后的哈里斯鷹算法優化概率神經網絡(Probabilistic Neural Networks,PNN),并與PNN和BP算法的分類結果進行了對比。結果表明所提出的故障檢測模型要優于另外兩種算法。

核極限學習機(Kernel Extreme Learning Machine,KELM)自提出以來,已被應用于多個領域。馬超等[11]將KELM用于液壓泵在線預測,為液壓泵的預測控制和故障預測提供了參考。陳紹煒等[12]建立了基于KELM的模擬電路故障診斷模型,并且與支持向量機和極限學習機進行對比,結果顯示準確率優于另外兩個模型。劉鷺航等[13]采用半監督極限學習機進行故障檢測,解決了由于控制力矩陀螺故障數據不足導致的結果不準確的問題。馮磊華等[14]用KELM優化電站鍋爐,有效減少了有害氣體的排放。

本文依據KELM在分類和擬合方面具有強大適應性的優點,將其應用于液體火箭發動機故障檢測。依據蛇優化算法(Snake Optimizer,SO)較強的尋優能力和存在的一些不足,對SO進行了改進,并將改進后的算法用于優化核函數參數和懲罰因子。最后基于歷史樣本數據,對建立的故障檢測模型進行了實驗仿真。

1 核極限學習機

單隱層前饋神經網絡在進行訓練時,多采用梯度下降法。傳統的學習算法存在訓練速度慢、易陷入局部最優、學習速率難以選擇等缺點。鑒于此,Huang教授提出了極限學習機(Extreme Learning Machine,ELM)算法[15]。該算法僅需設置隱含層的個數即可,輸入層與隱含層之間的權值和隱含層的閾值由隨機數生成。該方法具有訓練速度快、泛化性能好等優點。算法結構如圖1所示。

圖1 極限學習機結構

通過圖1可以看出,網絡的輸出受隱含層的輸出和隱含層與輸出層之間連接權值β影響。隱含層的輸出由輸入層與隱含層之間的連接權值a、隱含層的閾值b以及隱含層的激活函數G(·)決定。而輸入層與隱含層之間的權值a和隱含層的閾值b由隨機數生成。在確定激活函數后,可以求得隱含層的輸出。因此,我們的目標是求得隱含層與輸出層之間的權值β。

以單個訓練樣本為例。假設網絡有n個輸入層,m個輸出層,l個隱含層。輸入層與隱含層之間的權值矩陣為al×n,隱含層閾值矩陣為bl×1,隱含層與輸出層之間的權值矩陣為βl×m。隱含層激活函數為G(·)。則網絡的輸出可以表示為:

(1)

式(1)可簡化為:

Hβ=YT

(2)

式中:H1×l為隱含層輸出矩陣,HT為輸出矩陣Y的轉置。為使得預測輸出和實際輸出誤差盡可能小。對以下方程組進行求解:

(3)

得:

(4)

其中:H-1為輸出矩陣H的逆矩陣。

在2012年,Huang等將支持向量機中核函數的思想引入ELM,提出了核極限學習機[16]。在保證網絡結構泛化能力的前提下,提高了系統的魯棒性和運算速度,且算法的實現也較為簡單。

首先引入懲罰因子C,將隱含層與輸出層之間的權值矩陣β重新定義為:

(5)

將核函數矩陣ΩKELM代替HHT,可得:

(6)

那么,KELM的輸出函數為:

(7)

本文核函數采用徑向基(RBF)核函數,其數學表達形式為:

(8)

其中:σ為核函數參數。

在實際應用中,核極限學習機(KELM)的核函數參數σ和懲罰因子C對算法的輸出結果影響較大,但其具體數值的確定又較為困難。學者們一般通過選取不同的數值進行多次嘗試,選擇輸出結果較好的一組數值作為參數。但該方法需要消耗大量的時間,且存在隨機性。鑒于此,本文采用一種新的群體智能算法對KELM模型參數進行尋優,以確定模型的最優參數。

2 ISO-KELM故障檢測模型

1.1 蛇優化算法

蛇優化算法(SO)是由Hashim和Hussien兩位學者根據蛇的交配行為所提出的一種新的元啟發式算法[17]。該算法根據蛇在低溫和食物充足的條件下進行交配這一特性,將算法流程分為探索和開發兩個階段。首先將所有個體劃分為雄性種群和雌性種群,在整個算法流程中,兩個種群的位置更新公式完全相同。因此下文僅對雄性種群更新公式進行介紹。

食物數量Q和溫度T的更新公式為:

(9)

(10)

式中:N為最大迭代次數,n為當前迭代次數,c1為常數,設置為0.5。可以看出,食物數量隨著迭代次數的增加而增加,溫度隨著迭代次數的增加而降低。

當Q<0.25時,算法處于探索階段,種群個體通過移動自身位置來尋找食物,更新公式為:

Xi(t+1)=Xrand(t)±c2×A×

((Xmax-Xmin)×r+Xmin)

(11)

(12)

式中:Xi為更新后的雄性個體位置,fi為該個體的適應度。Xrand為隨機雄性個體,frand為隨機雄性個體的適應度。Xmax和Xmin分別為求解問題的上邊界和下邊界。r為0～1之間的隨機數。c2為常數,設置為0.05。

當Q>0.25時,算法進入開發階段。在該階段,當T>0.6時,雄性個體在食物周圍進行開發,其更新公式為:

Xi(t+1)=Xfood±c3×T×r×(Xfood-Xi(t))

(13)

式中:Xi為雄性個體位置,Xfood為所有種群中最優個體的位置。c3為常數,設置為2。

當T≤0.6時,雄性個體將進入戰斗模式或交配模式,由隨機數決定。戰斗模式更新公式為:

Xi(t+1)=Xi(t)+c3×Fm×r×

(Q×Xbest,f-Xi(t))

(14)

(15)

式中:Xi為雄性個體位置,fi為其適應度。Xbest,f為雌性群體中的最優個體位置,fbest,f為其適應度。

交配模式更新公式為:

Xi,m(t+1)=Xi,m(t)+c3×Mm×r×

(Q×Xi,f(t)-Xi,m(t))

(16)

(17)

式中:Xi,m為雄性個體位置,fi,m為其適應度。Xi,f為雌性個體位置,fi,f為其適應度。

交配之后有50%的概率會產生后代,用以代替雄性種群中的最差個體。

2.2 蛇優化算法改進

蛇優化算法(SO)的初始種群由軟件的隨機數函數生成,可能會使得初始個體離最優點較遠,導致算法尋優能力不足;SO探索和開發階段的轉換由食物數量(Q)來決定。由于Q的大小僅受迭代次數影響,使得SO進入開發階段較晚,導致算法后期尋優能力不足;同時,SO后期種群多樣性減少,難以跳出局部最優點。

針對以上問題,分別提出以下3點算法改進策略。

2.2.1 Tent映射

針對初始化種群離散度不高,導致算法尋優能力下降的問題。采用Tent混沌映射對種群進行初始化操作。Tent映射表達式為:

(18)

本文將α的數值設置為0.499。因為當α等于0.5時,在經過50次左右的迭代后,種群會收斂至0,失去遍歷性。

2.2.2 動態策略

針對算法較晚進入開發階段,導致尋優能力較弱的特點,采用動態策略轉換探索和開發階段。為了使SO提前結束探索階段,增加開發階段的迭代次數,采用以下動態策略控制階段轉換:在探索階段,當種群最優適應度連續6代不發生變化的時候,SO進入開發階段。動態策略公式為:

D(t+1)=c4×D(t)+|fbest(t)-fbest(t-1)|

(19)

式中:D為動態參數。fbest為種群最優適應度。c4為常數,設置為0.1。當D的值小于1×10-6時,SO進入開發階段。

此外,將常數c4引入探索階段雌性種群的位置更新公式,加快種群的收斂。由于SO的特殊性,在雌性種群快速收斂的同時,雄性種群依舊可以在全局進行遍歷。

2.2.3 柯西變異

針對SO后期易陷入局部最優的特點,采取柯西變異策略對陷入局部最優的種群進行處理。

柯西變異策略來源于柯西分布。柯西分布的概率密度函數為:

(20)

當a=1時,稱為標準柯西分布。在SO中,柯西分布隨機變量生成函數為:

μ=tan(π×(r-0.5))

(21)

r為0～1之間的隨機數。個體位置擾動公式為:

Xworst(t+1)=Xworst(t)×(1+μ)

(22)

式中:Xworst為最優適應度較差的種群。

進入開發階段后,當全局最優值連續6代沒有發生變化的時候,對兩個種群中最好適應度較差的群體進行柯西變異。

改進后的算法流程如圖2所示。

圖2 改進蛇優化算法流程圖

2.3 算法優化流程

針對KELM參數難以確定的問題,采用上文改進后的蛇優化算法對參數進行尋優。

整個算法流程如圖3所示。

圖3 ISO-KELM模型流程圖

具體尋優過程為:

1)導入數據,包括數據樣本和標簽;

2)將樣本劃分為訓練集和測試集;

3)對訓練集數據進行歸一化處理,再使用訓練集歸一化時的映射對測試集進行歸一化;

4)初始化ISO算法參數,包括種群數量,種群維度,種群上下限和測試函數;

5)建立ISO-KELM模型,對KELM參數進行尋優。具體過程如圖2所示;

6)將所求得的最優懲罰因子C和核函數參數σ賦予KELM;

7)使用優化后的KELM進行故障檢測;

8)對尋優結果進行評價對比。

3 實驗仿真

3.1 故障模式

本次實驗數據選取某型號液體火箭發動機歷史試車數據,共420組。正常數據和故障數據分別為210組。故障數據包括渦輪葉片損壞、燃燒室喉部燒蝕、氧化劑泵汽蝕、氧化劑泵管路堵塞和氧增壓系統減壓閥故障5種典型故障模式。同時,為了使所提出算法具有較高的準確性和適用性,選取14個代表性強且相關性弱的發動機參數作為輸入。

3.2 數據處理

本次實驗采用仿真軟件進行仿真。選取前42組數據作為測試集,剩余數據作為訓練集。訓練集中的前42組數據作為驗證集,并將驗證集的準確率作為ISO的適應度。

ISO參數設置如下:種群數量設置為30,種群維度為2,第一維代表懲罰因子C,第二維代表核函數參數σ。種群上限和下限分別設置為100和0.001。

3.3 結果對比

我們將核極限學習機(KELM)、蛇優化算法優化核極限學習機(SO-KELM)、改進后的蛇優化算法優化核極限學習機(ISO-KELM)3種模型的故障檢測結果和傳統BP神經網絡模型故障檢測結果進行對比。部分模型輸出結果如圖4所示。

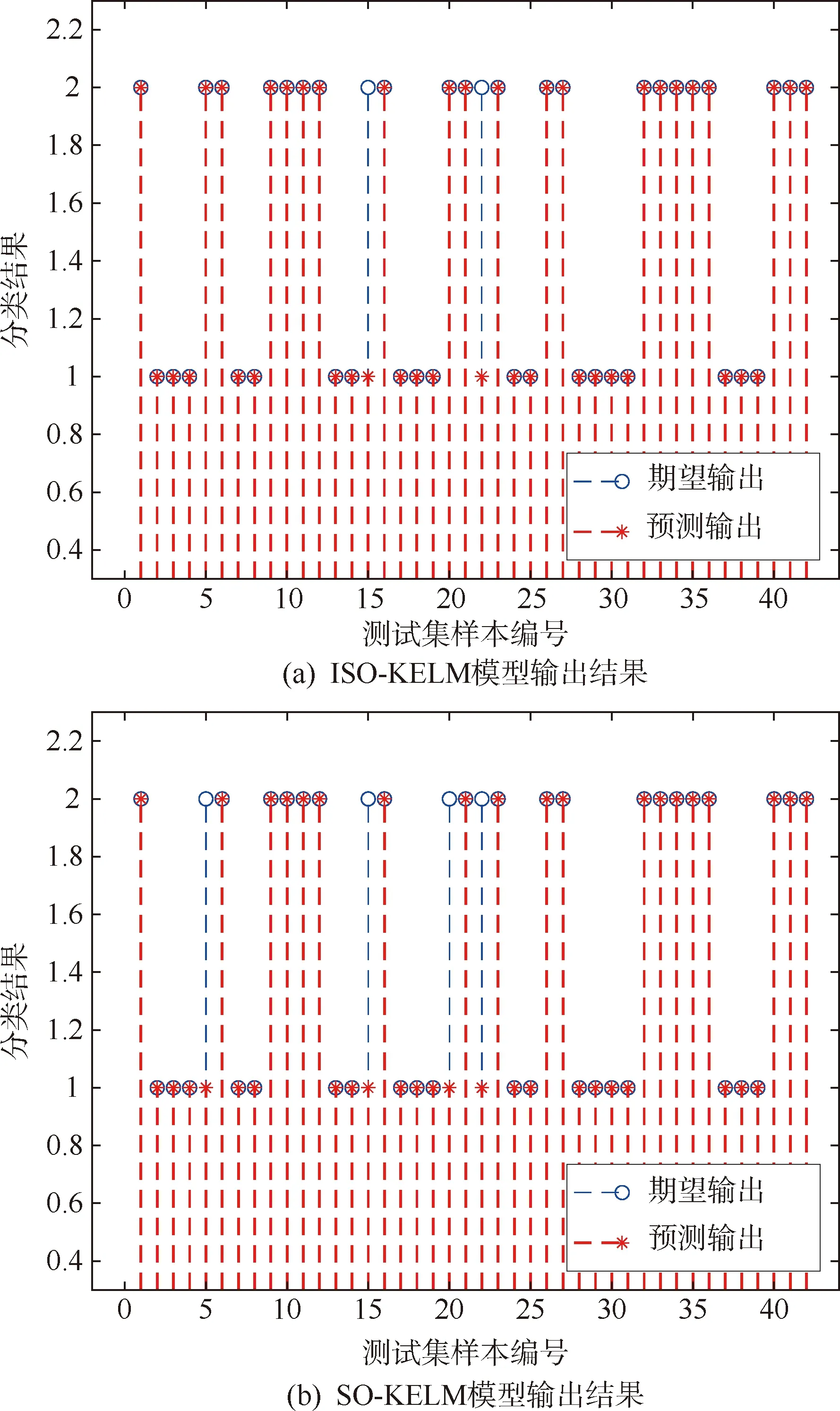
圖4 部分模型輸出結果

為便于直觀了解各個故障檢測模型的性能,采用誤報率、漏報率和準確率對4種模型進行評估。具體結果如表1所示。

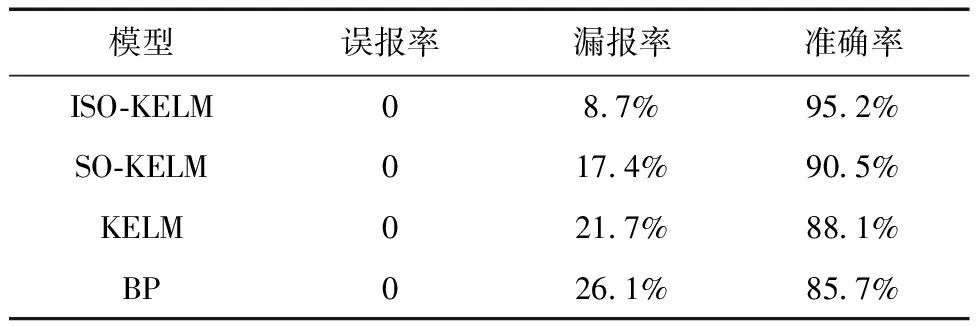
表1 模型檢測結果對比

通過表1可以看出,4種模型的誤報率均為0。漏報率的高低直接影響了模型的準確率。其中,KELM模型的漏報率相比于傳統BP神經網絡較低。同時,分別采用SO和ISO優化KELM后的模型均能提高檢測結果的準確率,且ISO-KELM模型的漏報率更低,檢測結果也更加準確。

為了驗證改進蛇優化算法具有更好的性能,采用適應度曲線作為算法的評估條件。

圖5分別為ISO和SO的適應度變化曲線。可以看出,在算法開始運行時,ISO的適應度低于SO的適應度,原因是ISO的初始種群遍歷性較強,在前期有更強的尋優能力。由于ISO在探索階段尋優能力有限,因此在前幾次迭代過程中適應度沒有發生變化。此時算法提前結束探索階段,進入開發階段。且在第18代尋得最優值。而SO整體收斂速度較慢,在第25代完成收斂,且尋得的最優值大于ISO。

圖5 算法適應度曲線

4 結論

使用改進蛇優化算法優化核極限學習機(ISO-KELM),并將其應用于液體火箭發動機故障檢測。可以得出以下結論:

(1)改進后的蛇優化算法可以提高種群前期的尋優能力,使種群提前進入開發階段,加快后期收斂,且收斂能力更強;

(2)ISO可以和KELM模型相結合,通過ISO獲得KELM模型的最優參數,從而實現對液體火箭發動機故障的有效檢測;

(3)仿真實驗表明,所提出ISO-KELM故障檢測模型的準確率優于傳統BP神經網絡故障檢測算法,實驗結果更加理想。