含非線性時間項的無偏灰色模型構建與應用

黃渝晴, 劉曉梅, 高美娜

(上海第二工業大學a. 計算機與信息工程學院;b. 數理與統計學院,上海 201209)

0 引言

自鄧聚龍教授1982 年提出灰色系統理論以來,灰色預測模型因其建模過程簡單、所需樣本少等優點,已經成功地應用于工業、農業、科技、軍事等眾多領域[1-2]。GM(1,1) 模型是灰色預測模型的經典形式,但學者們發現即使原始數據完全符合齊次指數規律,GM(1,1)模型也不能完全擬合原始序列,進而提出了無偏GM(1,1)模型的概念[3],并通過采用參數修正、調整灰導數和背景值等方法實現了無偏GM(1,1) 模型的構建[4-7], 使模型滿足協調性條件,實現從差分到微分的統一, 提高模型的擬合精度。隨后學者們對模型結構較簡單的NGM(1,1,k) 模型[8-9]、Verhulst 模型[10-13]、灰色Bernoulli 模型[14]進行了無偏性研究,提高了模型擬合精度,拓展了適用范圍。

但隨著各類系統不斷涌現出新特性、新問題,多種復雜的灰色模型被提出, 譬如: 灰色Riccati 模型[15-17]、分數階灰色模型[18-20]、時間冪次項灰色模型(GM(1,1,tα))[21-25]、時間項灰色模型等, 其中從灰作用量出發所構建的含多項式時間項灰色模型[26-28]具有一定的普適性, 極大地拓展了灰色模型的應用范圍, 可以用于擬合齊次、非齊次指數或者振蕩性數據。學者們在此基礎上也對原始序列采用分數階累加算子、對模型采用分數次冪時間項等方面進行改進[29-30],進一步提升了含時間項灰色模型的普適性。在含多項式時間項灰色模型中, 模型NGM(1,1,k)是最簡單的,因其模型結構簡單,易于構建無偏模型,但對于一般的含多項式時間項模型(也包括時間冪次項GM(1,1,tα)模型),因其白化方程離散時間響應函數的遞推公式難以從時間響應函數表達式推出,所以難以通過建立與參數估計遞推公式的等價關系來獲得無偏參數估計,因此,含時間項無偏灰色模型的研究也比較少。

本文以二次多項式時間項為例提出了含時間項無偏灰色模型的直接建模法。首先引入新變量, 借助于矩陣微分方程的解直接建立了白化方程離散時間響應函數的遞推關系,并與參數估計遞推關系建立等價關系,獲得了模型的無偏參數估計,構建了含二次多項式時間項的無偏灰色模型,并證明了此模型具有嚴格含線性時間項的非齊次指數序列重合性; 其次,在無需給出白化方程解析解的條件下,根據精細積分法直接進行模型的模擬(預測), 其計算結果可達到計算機精度,并運用最優化理論探討了模型基值修正;最后,以嚴格含線性多項式時間項非齊次指數序列和能源消費量2 個實例,驗證了本文模型的有效性和實用性。

1 含二次多項式時間項無偏灰色模型構建

定義1設原始序列為

其1-AGO 序列為

式中:x(1)(k) =(z(1)(2),···,z(1)(n) 為X(1)的緊鄰均值生成序列;z(1)(k)=(x(1)(k)+x(1)(k ?1))/2,k=2,3,···,n。

定義2稱x(0)(k)+az(1)(k)=b0+b1k+b2k2為含二次多項式時間項灰色模型(GMP(1,1,t2))的基本形式。稱

為GMP(1,1,t2)模型的白化微分方程。a反映了序列的發展態勢(本文只研究a ?= 0 的情況),b0為灰作用量,b1,b2為時間修正項。

特別地,當b1=0,b2=0 時,GMP(1,1,t2)模型退化為GM(1,1) 模型; 當b2= 0 時, GMP(1,1,t2)模型退化為NGM(1,1,k) 模型; 當b1= 0 時,GMP(1,1,t2) 模型退化為含時間冪次項模型GM(1,1,t2)。

1.1 無偏GMP(1,1,t2)模型參數辨識

為了獲得無偏GMP(1,1,t2) 模型的參數估計,需首先構造遞推關系,令

則GMP(1,1,t2)模型的白化微分方程(1)轉變為

式中,A=。

根據微分方程解的理論可知式(2)的解析解在t=k時的表達式為:y(k) = eA(k?1)y(1), 且易得y(k)=eAy(k ?1)。

定理1白化方程(1) 離散時間響應函數的遞推關系為

其中:

證明記由矩陣的運算可知

將其代入eA的Taylor 展開式,可得

又因D2=Dn= 0,n≥3,則上式化簡后可得

其中,u1、u2、u3、u4如定理1 中所給。并將其代入y(k)=eAy(k ?1)可得

從式(3)可以看出,后面3 個等式是恒成立的,所以式(3)轉化為

即得結論,證畢。

利用最小二乘法, 可知u= (u1,u2,u3,u4), 參數估計的法方程組為

將其記為

定理2Bu=Y中參數的最小二乘估計為

以下根據直接建模法, 利用定理1 獲得無偏GMP(1,1,t2)模型a、b0、b1、b2的參數估計。

定理3無偏GMP(1,1,t2)模型的參數估計為其中

1.2 無偏GMP(1,1,t2)模型的預測

通常灰色模型參數識別后, 直接代入白化方程的解析解進行模擬和預測,但當時間項冪次比較高時,解析解的表達式是非常繁瑣的,不利于求解,并且由于計算機字長的限制,可能會進一步引入舍入誤差。本文引入了精細積分法, 在無需求出其解析解的前提下,只需要根據估計的模型參數即可求出其數值解,并且解的精度可以達到計算機精度。精細積分法是鐘萬勰院士等[31]針對齊次微分方程所提出的,其核心是精細計算其微分方程通解中的傳遞矩陣Mτ=exp(Aτ),τ為步長。具體為:將步長切分為2N份,N為正整數(稱為精細參數),則傳遞矩陣Mτ可寫為

當2N很大時,exp(Aτ/2N)=E+A·τ/2N,其中E為單位矩陣,記S=A·τ/2N,則傳遞矩陣Mτ就可寫為

而(E+S)(E+S) =E+2S+S2,因為S很小,當它與單位矩陣相加時就成為其尾數,在計算機舍入操作中其精度將喪失殆盡,故采用如下程序降低舍入誤差(先將小量相加,再與單位矩陣相加)。

使數值解的精度基本上可以達到計算機精度。精細積分法中雖然步長變小了,但傳遞矩陣Mτ只需生成一次就可終身使用,計算量并沒有增大,是一種高精度的計算方法。

定理4序列X(0)、X(1)和無偏GMP(1,1,t2)模型中參數a、b0、b1、b2估計值如定理3 所述,取x(1)(1) =X(0)(1),y(1)(1) = (x(1)(1),1,1,1), 則序列?y的遞推公式為

式中,k=2,3,···,n。

本文利用直接建模法建立參數a、b0、b1、b2的無偏估計,根據精細積分法給出(1)(k)的預測, 稱此模型為基于精細積分法的無偏GMP(1,1,t2)灰色模型(簡記:HUGMP(1,1,t2))。

2 無偏GMP(1,1,t2)模型的性質

引理1GMP(1,1,t2)模型的離散時間響應函數為

定理5若原始數據序列嚴格服從含線性時間項的非齊次指數規律

式中:k= 1,2,···,n;q ?= 0;c1,c2,c3為任意常數,則無偏GMP(1,1,t2)模型能夠完全擬合此非齊次指數規律。

證明根據原始序列x(0)(k)可得

與式(3)進行比較,可得

再根據定理3 可知

利用引理1 可得

將此代入式(6),可得

與(0)(k)相同,故此模型具有含線性時間項的非齊次指數規律。證畢。

定理6設非負序列G(0)為X(0)的數乘變換序列, 且g(0)(k) =ρx(0)(k),ρ為非負常數。對非負序列X(0)={x(0)(1),x(0)(2),···,x(0)(n)}和G(0)={ρx(0)(1),ρx(0)(2),···,ρx(0)(n)}分別建立無偏GMP(1,1,t2)模型,記,0,1,2和,0,1,2分別為序列X(0)和G(0)的模型參數估計值, 則=0,1,2。

證明記X(0)的各參數如定理2 所示,=,不妨設BTB的伴隨矩陣為

故

記G(0)的各參數也如定理2 所示,則

定理7設非負序列G(0)為X(0)的數乘變換序列, 其中g(0)(k) =ρx(0)(k),ρ為非負常數。記和分別為序列X(0)和G(0)的無偏GMP(1,1,t2)模型的模擬值(預測值),則

證明根據引理1 和定義1 可知,

故還原的模擬值為

其中,k=2,3,···,n。證畢。

定理6 和定理7 稱為無偏GMP(1,1,t2)模型伸縮變換一致性定理,故對原始序列進行數乘變換不影響模型模擬和預測值的相對誤差。因此, 在原始序列數量級較大時可以預先進行必要的數乘變換,以有效解決模型的病態問題。

3 模型的迭代基值優化

通常考慮給迭代初值增加一個修正項以盡可能消除迭代初始值對模型擬合值的影響,反向抵消初始值帶來的偏差。選擇迭代基值在HUGMP(1,1,t2) 模型基礎上加上基值修正項ε,即利用式(5)計算再取第1 個分量結果作為,進而構建了1 個無約束的優化模型

由此優化模型可以看出,P為關于ε的二次多項式, 且ε2項系數為正實數。故由極值的必要條件(dP/dε= 0) 得ε值, 再由極值第二充分條件(d2P/dε2>0)知函數P的最小值點為ε。

基于迭代基值優化的HUGMP(1,1,t2) 模型的具體計算步驟如下:

Step 1 識別參數,根據式(4)利用最小二乘法獲得參數的估計值

Step 3 迭代基值優化, 根據精細積分法, 利用式(5)求, 進而獲得并根據式(7)求出HUGMP(1,1,t2)模型的迭代基值修正項ε;

Step 4 模擬預測, 在優化初始值的基礎上,求出(1)(k+1), 并根據式(6) 還原原有序列數值(0)(k)。

4 算例分析

4.1 HUGMP(1,1,t2)模型無偏性驗證

為了驗證HUGMP(1,1,t2)模型的無偏性,下面將從嚴格含線性時間項的非齊次指數序列和不同指數的含線性時間項非齊次指數序列2 個方面來驗證本文模型的無偏性。

例1取序列x(0)(k) = 2k+ 3k+ 5,k=1,2,···,6, 構建HUGMP(1,1,t2) 模型。圖1 給出了取不同精細參數N時基于迭代基值優化的HUGMP(1,1,t2) 模型的平均絕對百分比誤差MAPE (mean absolute percentage error, MAPE =· 100%) 結果, 縱坐標為MAPE 的對數值, 即log10MAPE。從圖1 中可以看出,隨著精細參數N的增加, MAPE 逐漸穩定在10?13,說明所設計的算法能夠嚴格擬合非齊次指數序列,也驗證了此模型的無偏性。

根據圖1 可知,精細參數N=40 時模擬精度最高,N≥45 時模擬精度趨于穩定,故表1 列舉了無偏GMP(1,1,t2)在不同精細參數(N= 40,45)、不同模擬方法(直接代入解析解或采用精細積分法)、是否采用迭代基值優化的各種情況下的模擬精度。可以看出,當選取合適的精細參數N時, 基于精細積分法的無偏GMP(1,1,t2)模型的模擬精度要優于采用解析解獲得的模擬精度。由于計算機舍入誤差的存在,對此嚴格序列采用迭代基值優化的方法基本上與未采用的結果相差無幾,但均優于采用解析解模擬的無偏GMP(1,1,t2)模型, 說明本文所設計算法的有效性。

表1 嚴格含線性時間項非齊次指數序列擬合精度Tab.1 The fitted precisions of rigorous nonhomogeneous exponential series with linear time terms

例2取x(0)(k)=3qk+5k+8,k=1,2,···,6。分別設q= 0.5,3,6,9,12, 所得原始序列如表2 所示(表中數據通過四舍五入保留小數點后四位), 采用HUGMP(1,1,t2) 建模(取精細參數N= 40), 計算得到各序列的參數和擬合情況如表3 所示。從表3 中可以看出, 除去由計算機數據處理精度造成的誤差,參數c1,c2,c3的擬合精度都比較高,其中對q的擬合最好,序列擬合精度高;當序列增長比較平緩時,模擬的精度相對較差,MAPE 為2.869E?007,而q= 3 時,模擬精度最好,MAPE 為8.317E?013。通過對多個非齊次指數序列的計算,再一次證明了所提出的模型具有無偏性。

表2 多個含時間項非齊次指數序列數據Tab.2 Nonhomogeneous exponential series in different time terms

表3 多個指數序列的HUGMP(1,1,t2)模型參數及誤差Tab.3 The parameters estimations and their errors of HUGMP(1,1,t2)model for different exponential series

4.2 實例分析

例3選取2005—2016 年上海市能源消費量(單位: 萬t 標準煤) 為模擬數據, 2017—2019 年上海市能源消費量為預測數據, 構建GM(1,1) 模型、無偏NGM(1,1,k)模型、GMP(1,1,t2)模型以及HUGMP(1,1,t2)模型。

GM(1,1)模型:

其時間響應方程為

無偏NGM(1,1,k)模型:

其時間響應方程為

GMP(1,1,t2)模型:

其時間響應方程為

優化HUGMP(1,1,t2)模型:

各模型擬合(預測) 值和相對百分比誤差(APE%) 結果見表4, 從表中可以看出, 隨著時間項冪次的增大,模型的擬合和預測精度逐步提高,平均擬合誤差MAPE_sim 從GM(1,1)模型(含零次多項式時間項) 2.38% 降至無偏NGM(1,1,k) 模型(含一次多項式時間項)0.89%、GMP(1,1,t2)模型(含二次多項式時間項) 0.80%, 平均預測誤差MAPE_pre也從4.22% 降至1.60%。并且本文所提出的HUGMP(1,1,t2) 模型無論是擬合誤差還是預測誤差均低于傳統的GMP(1,1,t2)模型,提高了擬合(預測)精度,同時也表明了所構建無偏模型的有效性。

表4 各種模型擬合(預測)結果對比Tab.4 Comparisons of the fitted and predicted results with different methods

例4選取《2019BP 世界能源統計年鑒》中2001—2018 年石油消費量進行建模,其中2001—2015 作擬合, 2016—2018 年作預測分析。分別采用GM(1,1)、NGM(1,1,k)、Verhulst、ARMA(1,1)、GRM(灰色Riccati 模型)[17]、HUGMP(1,1,t2) 建模。由表5 和圖2 可見, NGM(1,1,k)、Verhulst 2 個模型的結果偏離實際值比較大, 擬合(預測) 效果差, ARMA(1,1) 的模擬結果有振蕩性,擬合能力不好, GM(1,1) 模型的預測能力較弱。GRM、HUGMP(1,1,t2)模型的模擬(預測)值與實際值基本重合。進一步從表6 和圖3 中可以看出,GM(1,1)模型、NGM(1,1,k)、Verhulst、ARMA(1,1)、GRM 的最大APE 為10.2829%、54.3376%、75.2261%、9.6100%、7.0255%, 而本文模型的最大APE 為6.5917%。本文模型的MAPE 為1.8343%,低于其他模型的3.6436%、11.9337%、34.9516%、3.8968%、2.0580%。綜合來看,ARMA(1,1)、GRM、HUGMP(1,1,t2)能很好地擬合石油消費量的趨勢,并且HUGMP(1,1,t2)是最好的模型。

表5 原油消費各模型的擬合值和預測值Tab.5 The fitted and predicted values of different models in oil consumption

表6 原油消費各模型擬合和預測誤差Tab.6 The fitted and predicted errors of different models in oil consumption

圖2 各模型擬合(預測)值與實際值對比Fig.2 Comparisons of the fitted and predicted values of different models with actual values

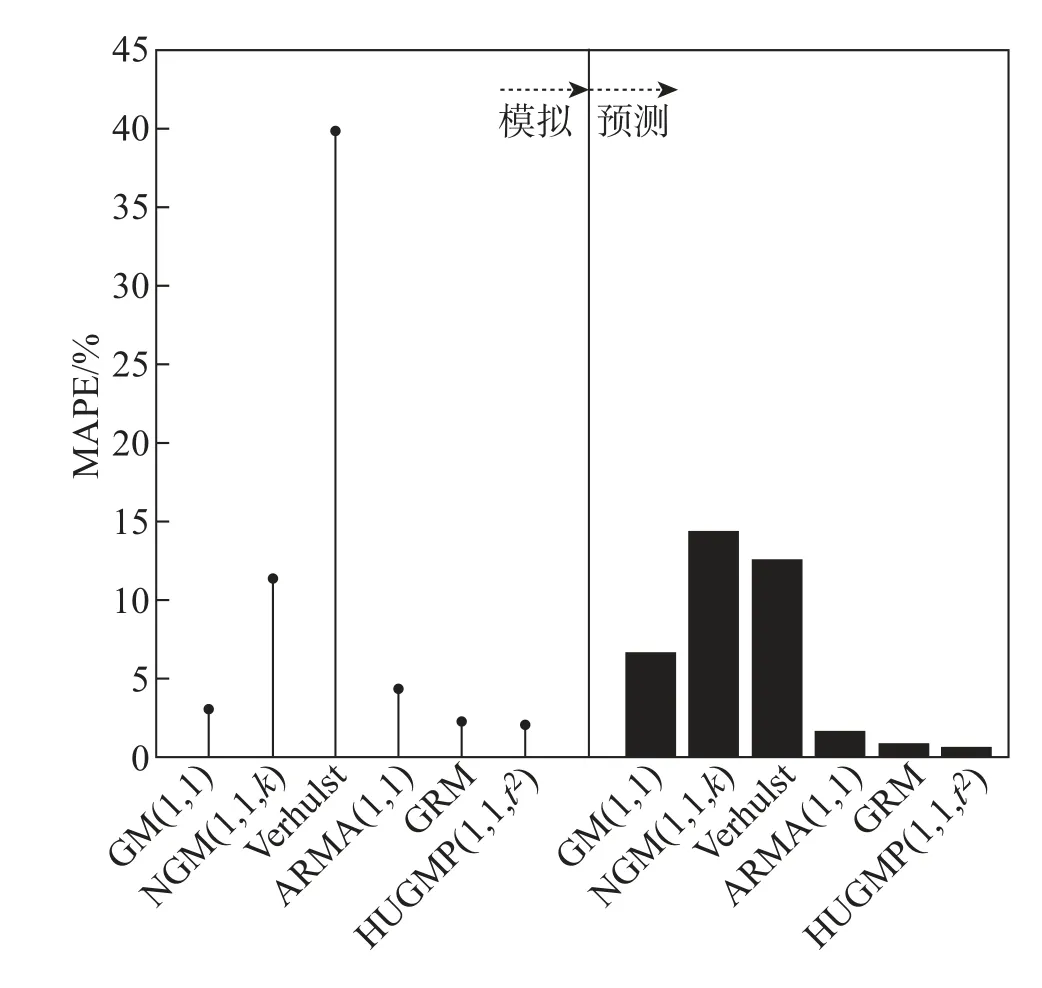
圖3 各模型擬合(預測)誤差Fig.3 The fitted and predicted errors of different model

5 結論

本文對含二次多項式時間項的灰色模型進行了研究, 提出了基于精細積分法的無偏灰色模型HUGMP(1,1,t2), 對該模型的建模機理和實際應用進行了研究,具體結論如下:

(1) 無需已知白化方程解析解的前提下, 給出了無偏GMP(1,1,t2)模型的參數估計,構建了無偏GMP(1,1,t2) 模型, 證明了此模型具有含線性時間項非齊次指數序列的重合性以及具有伸縮變換的一致性,具有較好的模擬和預測能力;

(2) 無需已知白化方程解析解的前提下, 采用精細積分法給出GMP(1,1,t2) 模型的模擬(預測)值,建立了基于精細積分法的無偏GMP(1,1,t2)模型, 即HUGMP(1,1,t2) 模型, 并利用最優化理論及Matlab 編程對模型HUGMP(1,1,t2) 的迭代基值進行了優化;

(3) 從嚴格含線性時間項非齊次指數序列和能源消費量兩個實例中可以看出, 所構建的HUGMP(1,1,t2) 模型能嚴格模擬含線性時間項非齊次指數序列, 驗證了此模型的無偏性, 且HUGMP(1,1,t2) 模型在模擬和預測精度優于傳統的GM(1,1) 模型, 也優于許多灰色預測模型NGM(1,1,k)、Verhulst 模型、GRM 模型等), 其模擬和預測結果都得到了明顯提高。