融入MATLAB 軟件的機械振動混合教學模式探索*

牛燕 姚明輝 吳啟亮

天津工業大學人工智能學院 天津 300387

0 引言

近年來，隨著科技的進步以及工業的發展，對工程結構性能的需求也逐漸提升，既要實現高性能，又要滿足高可靠性，而振動問題也必然成為亟須解決的關鍵問題。機械振動是機械、力學等專業重要的專業基礎課，是一門理論基礎要求高且綜合性強的課程。掌握振動的基本理論，合理地利用或避免振動，為學生提供基本的技能知識，是該課程的主要目標。本課程主要學習線性振動相關知識，從單自由度系統進行介紹，逐步擴展到多自由度系統，最后介紹連續體系統，講述不同系統相關的基本理論以及在工程中的應用。此課程可以滿足機械或結構振動相關崗位的需求，對于有興趣在振動方面進行深入研究的學生，可以繼續學習后續振動相關知識，例如非線性振動、隨機振動以及瞬態振動等。機械振動課程需要扎實的數學知識和大量的計算過程，內容抽象晦澀，學生反映課程枯燥無趣，難以理解，所以傳統的機械振動教學模式效果不佳，迫切需要探索新的教學模式。

機械振動課程中涉及大量的公式推導，如果純粹是教師和學生自己推導，會浪費大量的時間，也打擊學生的積極性和主動性。以求解固有頻率和主振型為例，主要是利用線性代數中的求解特征值和特征向量知識。此時，MATLAB 軟件因其強大的計算功能，可用于輔助計算。此種融合MATLAB 軟件的混合教學模式既可以將學生從枯燥乏味的公式推導中解脫出來，還可以提高計算的準確性，激發學生的科研興趣。學生熟練掌握MATLAB 軟件后，只需要掌握基本原理和求解方法，耗時耗力的求解過程通過輔助軟件進行，學生可以對知識進行靈活運用并拓展思維，有更多的精力和興趣放在重點、難點知識上，在實踐中理解理論知識，在融匯理論知識的基礎上再進行實踐應用，實現“實踐—理論—實踐”的飛躍[1]，將理論和實踐融會貫通，做到學以致用。楊帆[2]利用MATLAB 軟件對簡諧波進行合成，利用軟件的可視化功能將抽象復雜的振動知識呈現出來。呂書峰等[3]利用MATLAB 軟件分別求解單自由度系統線性振動和非線性振動的幅頻特性曲線。

常年的學習過程中，學生理論知識水平掌握很扎實，但是也僅限于理論學習，在面對工程應用時往往會力不從心、無從下手，這不僅打擊他們學習的積極性，也會讓他們產生迷茫感。適當地混合教學模式可以充分調動學生的積極性，培養學生的創造性思維，寓教于樂，使學生主動探索書本上的知識，而不是被動接受教師的灌輸。

1 MATLAB 軟件的功能介紹

MATLAB 軟件是1982 年美國MathWorks 公司開發的一款高性能數值計算和可視化軟件，MATLAB軟件編程計算與人類進行計算的思路完全一致，無需專業的編程語言基礎，比其他高級語言更容易掌握，在工科專業中廣泛使用。以下是MATLAB 軟件一些常用的功能。

1.1 推導計算

MATLAB 軟件中函數非常全面，還有專門的Toolbox 工具箱，可以快速準確地解決復雜的數學計算，常見的案例為MATLAB 軟件在線性代數以及高等數學中的應用，例如快速求解矩陣的秩、行列式、特征值以及特征向量等。針對計算量非常大的情況，MATLAB 計算機輔助軟件的優勢就顯而易見，對于龐大的矩陣運算，計算機幾秒就可以準確計算出結果。

1.2 繪圖

MATLAB 軟件的一個重要優勢在于數據可視化[4]，工科專業中經常會遇到函數，有些函數過于抽象，難以直觀想象。通過MATLAB 軟件的繪圖功能，簡單的語句就可以將抽象函數具體化，因此在教學、科研中廣泛應用，例如最常用的二維圖形、三維圖形以及隱函數圖形的繪制。應用最為廣泛的二維曲線繪圖函數為plot 函數。將二維曲線繪圖函數plot 擴展到三維空間，可以利用plot3 函數繪制三維曲線。空間曲面是高等數學課程中常見的內容，也是比較抽象的內容，很難想象出來，此處可以利用MATLAB 軟件進行繪制。常用的繪制三維曲面的函數為surf 函數和mesh 函數，其中surf 函數用來繪制三維曲面圖，mesh函數用來繪制三維網格圖。此外還有很多繪制三維圖的函數，例如waterfall函數、contour3 函數、stem3 函數、bar3 函數等。

1.3 建模仿真

利用MATLAB 軟件進行建模或仿真十分便利，例如Simulink 系統，可以用來對各種動態系統的交互環境進行建模和仿真。此外，MATLAB 軟件的應用使得之前需要進行簡化假設的隨機因素、非線性因素等可以考慮在內，因此求解范圍更廣，準確性更高。在MATLAB 軟件中直接進行簡單編程也可以對方程進行數值仿真，例如高維非線性常微分方程的解基本難以求得，此時可以利用不同的算法進行數值仿真，通過仿真分析可以得出系統的響應曲線等等，從而對工程實踐進行指導，將數學知識與工程應用進行有效結合。

2 融入MATLAB 軟件的機械振動教學實踐

按照自由度進行分類，振動系統可以分為單自由度系統、多自由度系統和連續體系統（無限自由度系統）。首先以多自由度系統—彈簧質量塊系統為例，其次以連續體系統—薄板結構為例，引入MATLAB 輔助教學軟件，分別求解固有振動特性，用實例來探索混合教學模式的便利和優勢。

2.1 彈簧質量塊系統的固有振動特性求解實例

以一個三自由度的彈簧質量塊系統為例[5]，如圖1 所示，其中k1=3k，k2=2k，k3=k，m1=2m，m2=1.5m，m3=m，假設k=m=1，求系統的固有頻率和主振型。求解過程如下：

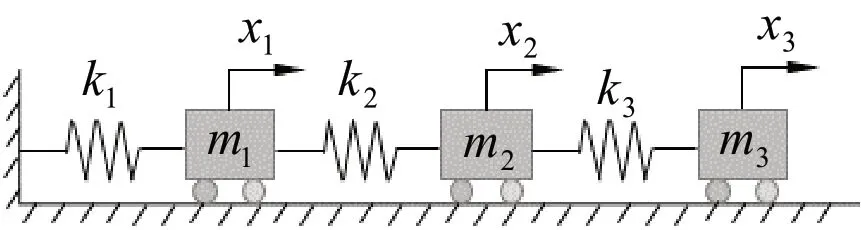
圖1 彈簧質量塊系統示意圖

首先取x1，x2和x3為廣義坐標，則三自由度系統的質量矩陣和剛度矩陣可以求解為：

系統自由振動的微分方程表示如下：

采用MATLAB 軟件進行求解，求解結果如圖2

圖2 MATLAB 軟件運行結果

所示，具體求解程序如下：

clear；

M = [2 0 0; 0 1.5 0; 0 0 1]; % 質量矩陣

K = [5 -2 0; -2 3 -1; 0 -1 1]; % 剛度矩陣

[PPP,lamuda] = eig(K,M); % 求解特征值和特征向量

np = sort(diag(lamuda)); % 求解出的特征值從小到大進行排序

frequency = sqrt(np) % 開根號得出固有頻率

for i = 1:1:3

Modeshape(:,i) = PPP(:,i); % 前三階振型

end

% 規定每一階主振型中最大的一個坐標幅值為1

f1 = 1/Modeshape(3,1);

Mode1 = f1 * Modeshape(:,1) % 第一階主振型

f2 = 1/Modeshape(3,2);

Mode2 = f2 * Modeshape(:,2) % 第二階主振型

f3 = 1/Modeshape(3,3);

Mode3 = f3 * Modeshape(:,3) % 第三階主振型

其中%后面內容是為方便理解添加的注釋，此部分內容在運行程序時不執行。首先求解三自由度系統的質量矩陣M和剛度矩陣K，利用eig函數求解特征值和特征向量，利用diag 函數得到對角線上的廣義特征值，再利用sort 函數進行排序，最后通過sqrt 函數開平方得到固有頻率。前面程序可以求解出相應的特征向量，假設每一階主振型中第三個元素為1，需要同時對前面的特征向量進行同比放大或縮小，也就需要引入系數f1、f2、f3，從而得到每一階主振型Mode1、Mode2 和Mode3。

運行結果如圖2 所示。

運用上述MATLAB 軟件進行求解，只需要寫出多自由度系統的質量矩陣M和剛度矩陣K，即可簡單求解出固有頻率和主振型。課程教學中，要求學生掌握基本的MATLAB 編程技能，使用此計算機輔助軟件對機械振動課程進行計算，還可以增加系統難度，鍛煉學生舉一反三的能力以及提升編程能力。此處只是一個簡單的三自由度系統，所以質量矩陣和剛度矩陣都是三階方陣，學生自己進行手動計算也可以很快得出結果。但是對于實際工程需求或者科研需求，系統的自由度往往很多，那么K和M就是高階方陣，計算過程很復雜，計算結果也容易出現錯誤，對于學生而言，手動推導是很頭疼的一件事，此時MATLAB 軟件的優勢顯而易見，學生只需要掌握計算方法和簡單的編程原理就可以準確求解，這對于解決學生面臨的實際工況或者激發學生科研興趣均有極大的幫助，也是探索混合教學模式的目的所在。針對手動難以求解的問題進行案例介紹，下面以一個連續體系統為例，探索MATLAB輔助計算機軟件的優勢，并采用繪圖功能生動形象地向學生展示理論基礎對應的工程應用。

2.2 薄板結構的固有振動特性求解實例

工程中常見的結構為連續體結構，例如梁、板、殼等結構，其固有頻率和模態振型也備受關注。求解過程比多自由度系統復雜很多，沒法直接列出質量矩陣和剛度矩陣。以板結構為例，簡單介紹一種求解方法，需要利用一階剪切變形理論對其進行動力學建模，分別推導出結構的動能和勢能表達式，利用瑞利—里茨法求解固有頻率和模態振型。連續體系統考慮為無限自由度系統，實際求解過程中可以發現考慮前五階或六階模態就可以收斂，一階剪切變形理論中有五個變量，再考慮前五階模態，計算量十分龐大，此過程如果手動推導難以實現，學生不僅耗時耗力，還很難保證結果的準確性。此時采用MATLAB 軟件進行計算非常便利，既可以保證計算推導的準確性，又能顯著提高效率，是科研工作中經常采用的方法。

以一塊長度為a=300 mm，寬度為b=300 mm，厚度為h=3 mm 的平板為例，如圖3 所示，板的邊界條件是懸臂邊界條件。假設材料屬性如下：楊氏模量為，密度為，泊松比為μ=3.0，利用MATLAB 軟件求解平板結構前五階無量綱固有頻率，與Gu 等[6]結果進行對比，如表1 所示，本文采用MATLAB 軟件求解得到的結果與參考文獻吻合得很好。

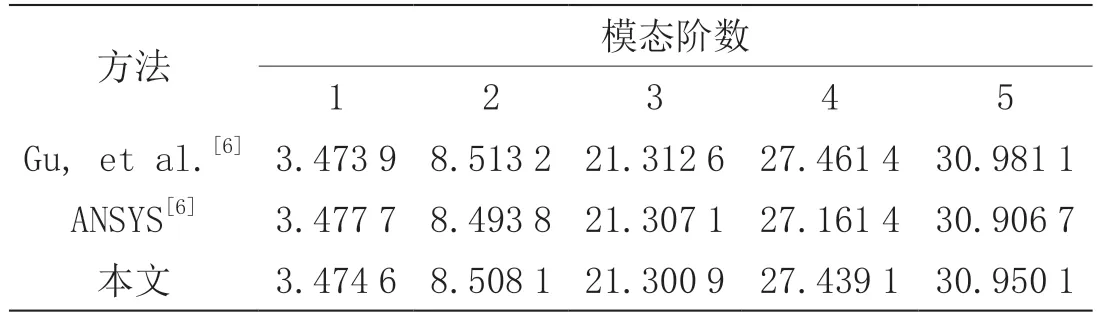
表1 平板結構前五階無量綱固有頻率對比

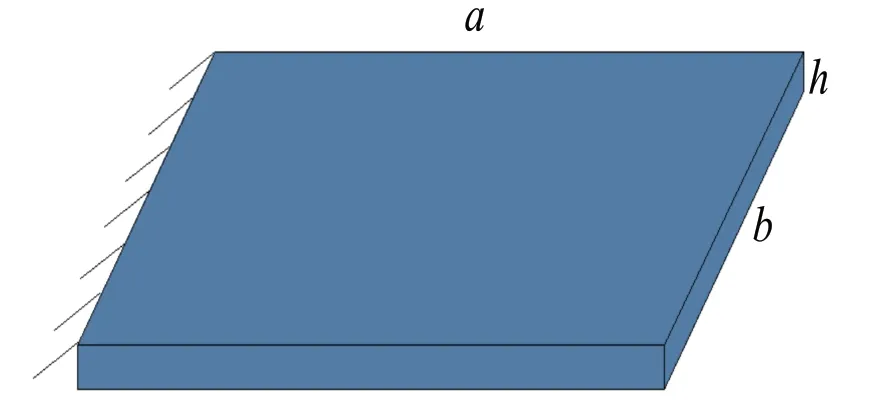
圖3 平板結構示意圖

工程中除了常用的固有頻率，模態也十分關鍵。通過模態分析可以了解結構各階模態的主要特性，進而預測結構的實際振動響應。因此，模態分析是進行結構設計和故障診斷所采用的重要方法之一。利用MATLAB軟件求解上述平板結構的模態振型圖，如表2 所示。利用軟件的繪圖功能和可視化功能向學生生動地展示平板的振動形式。傳統的課程教學中教師的講解很枯燥，學生也難以直觀想象平板究竟會出現何種振動形式，甚至于很難理解何為模態。但是采用混合教學模式，可以清晰地向學生展示出各階模態圖，由表中可以看出第一階模態振型為一階彎曲模態（First Bending mode，1B），第二階模態振型為一階扭轉模態（First Torsional mode，1T），第三階模態振型為一階邊緣彎曲模態（First Edgewise Bending mode，1EB），第四階模態振型為一階弦向彎曲模態（First Chordwise Bending mode，1CB），第五階模態振型為二階扭轉模態（Second Torsional mode，2T）[7]。單純聽教師在課堂上對固有振動特性相關知識進行講解，對于沒有工程背景或立體感比較差的學生來說很難理解，也會導致對本課程逐漸產生抵觸和厭學心理。然而對照表2，學生可以清晰地看出平板結構在懸臂邊界條件下的各階模態形式，也會形成一個立體的認識，甚至可以舉一反三，自己動手對不同邊界條件或者結構尺寸下平板結構的模態振型進行求解，極大地調動學生學習的積極性和探索心理，這也是大學或者研究生期間課堂教學的主要目的。

3 結束語

以求解多自由度系統和連續體系統的固有振動特性為案例，將MATLAB 輔助軟件融入機械振動課堂，探索混合教學模式的實用性和便捷性。在引導學生掌握固有振動特性含義的過程中，通過計算機仿真軟件生動直觀地向學生進行展示，這對于學生的理解和領悟有著極大的幫助。熟練掌握解決振動相關知識，對于很多工科專業學生來說至關重要，是學生解決工程實際所需的基本技能，也是后續進行科研工作的基礎。此外，將MATLAB 軟件融入實踐教學中，有助于緩解學生對于枯燥公式推導的抵觸心理，調動學生的課堂參與度并激發學習積極性，使學生產生濃厚的編程興趣。在機械振動課程教學中，教師多鼓勵學生對相關知識進行MATLAB 編程，培養學生的編程能力，并鍛煉學生進行自主學習，利用軟件編程來輔助解決機械振動相關知識，達到培養學生實踐能力和科研興趣的目的。