巖土體抗剪強度對抗滑樁內力分布規律影響研究
肖可洋
(江西省水投建設集團有限公司,江西 南昌 330000)
滑坡災害是全球范圍內廣泛發育的一種地質災害,由于其規模大、分布范圍廣和危害性大的特點,容易造成較大的社會影響。
抗滑樁由于施工簡單,治理效果優越而被廣泛使用在滑坡治理工程中。國內外許多學者針對抗滑樁的受力性能及治理效果展開了深入的研究。麥合木提江[1]基于Geo-studio軟件研究了抗滑樁對滑帶土受力的影響。結果表明,抗滑樁對于水文地質條件復雜的滑坡治理效果良好。平詩語等[2]基于FLAC 3D數值有限元研究了滑坡的演化模式對抗滑樁的加固樁位與嵌固深度的影響。結果表明,樁體的有效嵌固深度比與滑坡類型無關,樁的最有效加固樁位并不一定是最合理樁位。仉文崗等[3]基于可靠度理論研究了巖體參數空間變異性對抗滑樁受力的響應。結果表明,強度參數的空間變異性對邊坡的失效概率及抗滑樁響應有顯著影響,不考慮巖土體的空間變異性將導致邊坡失效概率增大及低估抗滑樁的樁頂位移。劉孟瀚等[4]基于極限平衡原理研究了樁前溶洞對抗滑樁嵌固段穩定性的影響,并基于極限平衡法提出了樁前存在溶洞時嵌固段承載力驗算方法。周德培等[5]采用理論分析手段研究了邊坡工程中抗滑樁合理樁間距。結果表明,其他條件不變的情況下,樁間距隨樁后土體內聚力和內摩擦角增大而增大,隨樁后推力的增大而減小。韓愛民等[6]基于數值模擬研究了影響樁間土拱效應因素。結果表明,土的泊松比、剪脹角和樁土接觸特征對土拱效應的影響最明顯。張建勛等[7]采用數值模擬研究了土體性質、群樁以及樁土接觸面性質等因素對土拱效應的影響。結果表明,樁間距是影響土拱效應的最主要因素。戴自航[8]基于理論分析研究了滑坡推力和樁前滑體抗力分布規律,并建立了相應的滑坡推力和土體抗力分布函數模型,為滑坡治理及抗滑樁的合理設計提供參考。
本文基于數值模擬,研究了巖土體抗剪強度參數對抗滑樁內力分布特征影響。
1 數值模型
1.1 模型建立
建立典型數值計算模型如圖1所示。邊坡坡角為15°。抗滑樁共前后兩排,長度均為16 m,樁徑為1 m,嵌固段長度為6~7 m,樁心距為4 m,前后兩排樁排距也為4 m。在滑體后方施加40 kN/m的水平均布荷載模擬滑坡推力。共建立10根樁,前后各5根。

圖1 有限元分析模型
1.2 計算參數
巖土體破壞準則采用摩爾-庫倫本構,抗滑樁采用各向同性完全彈性本構,鋼筋采用強化拉伸塑性應力-應變本構。巖土體及鋼筋混凝土的物理力學參數見表1所示。
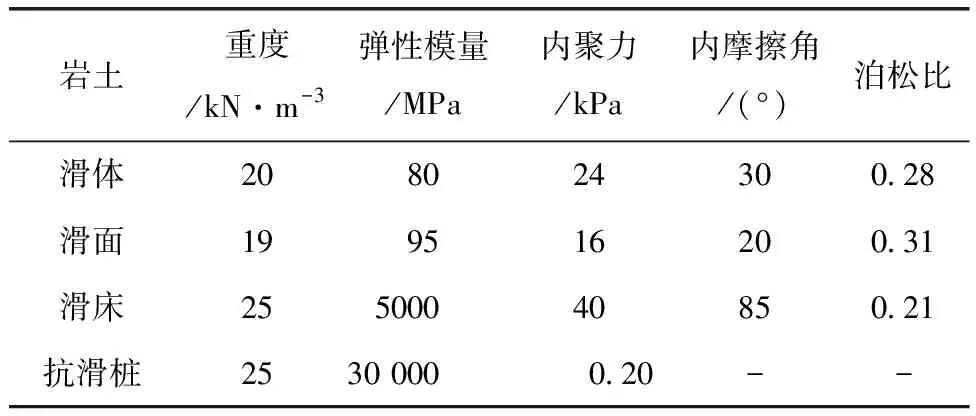
表1 材料物理力學參數值
2 計算結果與分析
2.1 內聚力影響
圖2匯總得到樁頂位移隨內聚力變化規律,結果表明,在其他條件不變的情況下,樁頂位移隨內聚力的增大而減小,但隨內聚力逐漸增大,位移減小速率越來越平緩。也即內聚力越小,滑坡推力越大,樁頂位移越大。
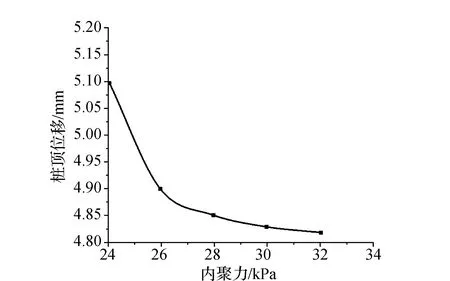
圖2 樁頂位移隨內聚力變化規律
圖3匯總得到前排樁和后排樁樁身彎矩隨樁長的變化規律。結果表明,其他條件相同的情況下,內聚力對樁身彎矩影響較小。兩排樁彎矩最大的位置均出現在樁身11 m的位置。
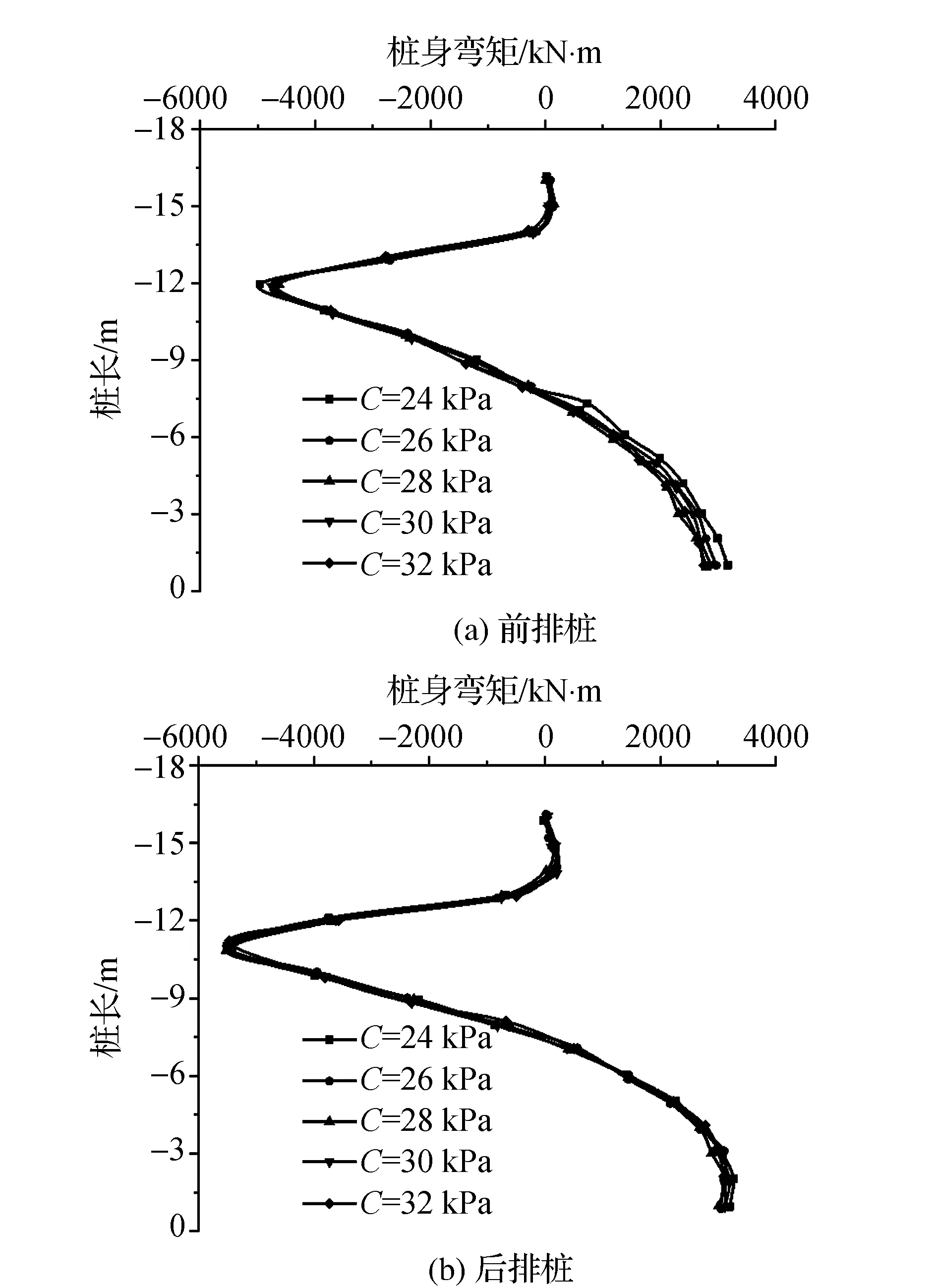
圖3 樁身彎矩隨樁長變化規律
進一步匯總得到樁身最大彎矩隨內聚力變化規律見圖4所示。結果表明,樁身最大彎矩隨內聚力的增大而減小。隨內聚力的增大,最大彎矩變化速率變平緩。對于后排樁而言,當內聚力分別為24 kPa、26 kPa、28 kPa、30 kPa和32 kPa時,彎矩最大值分別為5513 kN·m、5383 kN·m、5336 kN·m、5321 kN·m和5025 kN·m;前排樁的彎矩最大值分別為4742 kN·m、4644 kN·m、4596 kN·m、4571 kN·m和4557 kN·m。總之,內聚力越小,對樁身最大彎矩影響越大。
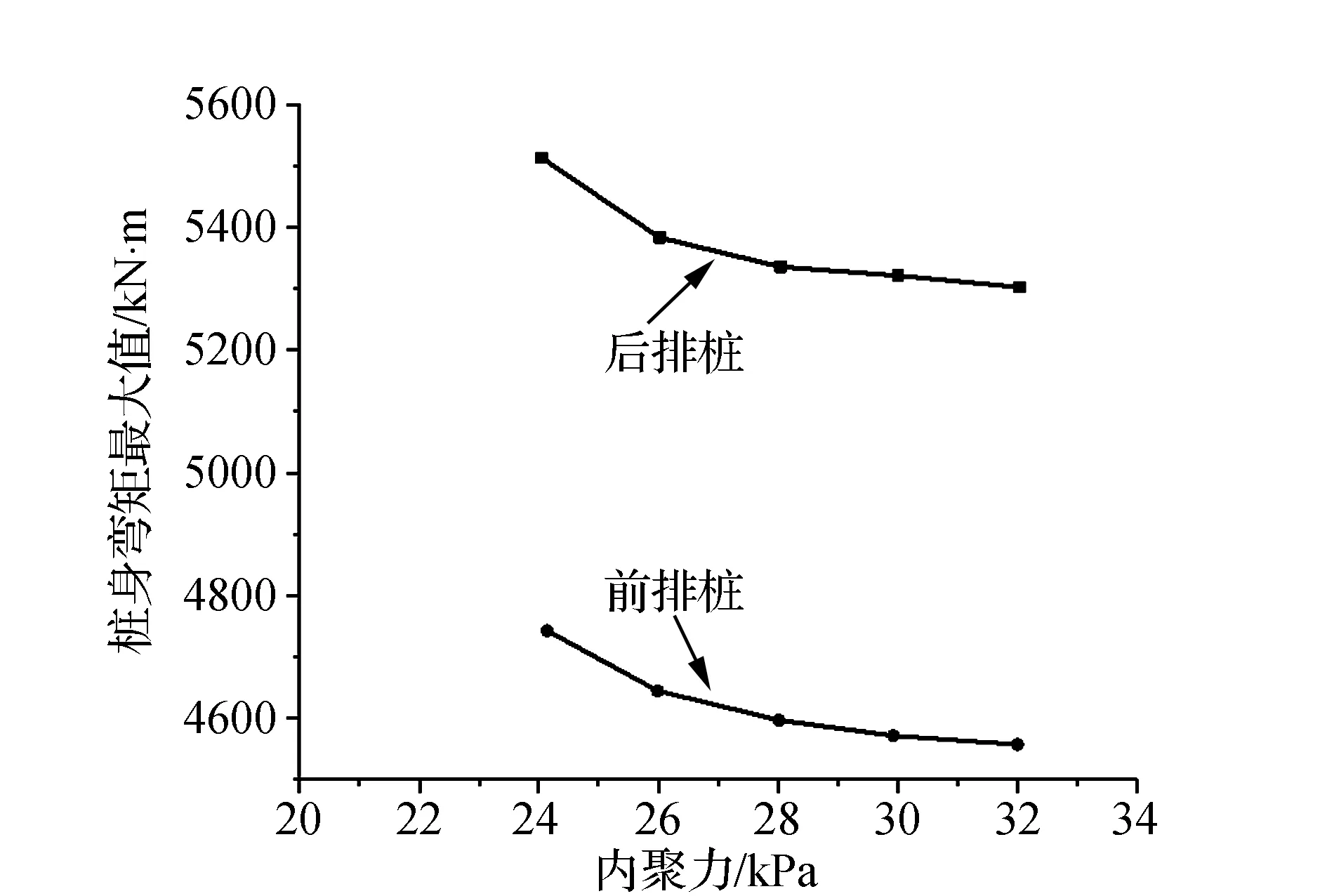
圖4 樁身彎矩最大值隨內聚力變化規律
圖5匯總得到前排樁和后排樁樁身剪力隨樁長的變化規律。結果表明,其他條件相同的情況下,內聚力對樁身剪力影響較小。
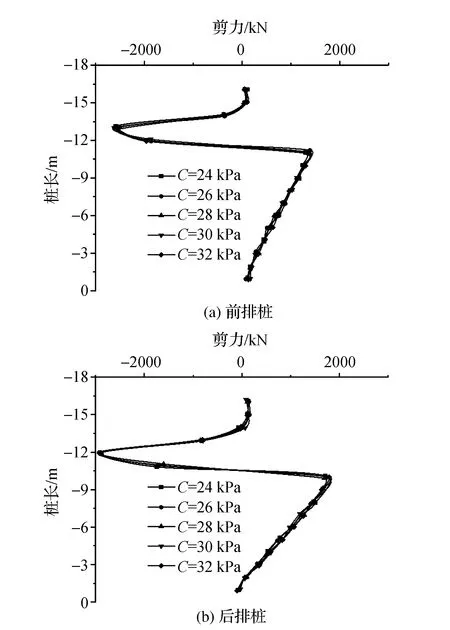
圖5 樁身剪力隨樁長變化規律
進一步匯總得到樁身最大剪力隨內聚力變化規律見圖6所示。結果表明,樁身最大剪力隨內聚力的增大而減小。隨內聚力的增大,最大剪力變化速率變平緩。對于后排樁而言,當內聚力分別為24 kPa、26 kPa、28 kPa、30 kPa和32 kPa時,后排樁剪力最大值分別為2951 kN、2869 kN、2856 kN、2849 kN和2850 kN;前排樁剪力最大值分別為2527 kN、2498 kN、2489 kN和2484 kN。總之,內聚力越小,對樁身最大剪力影響越大。
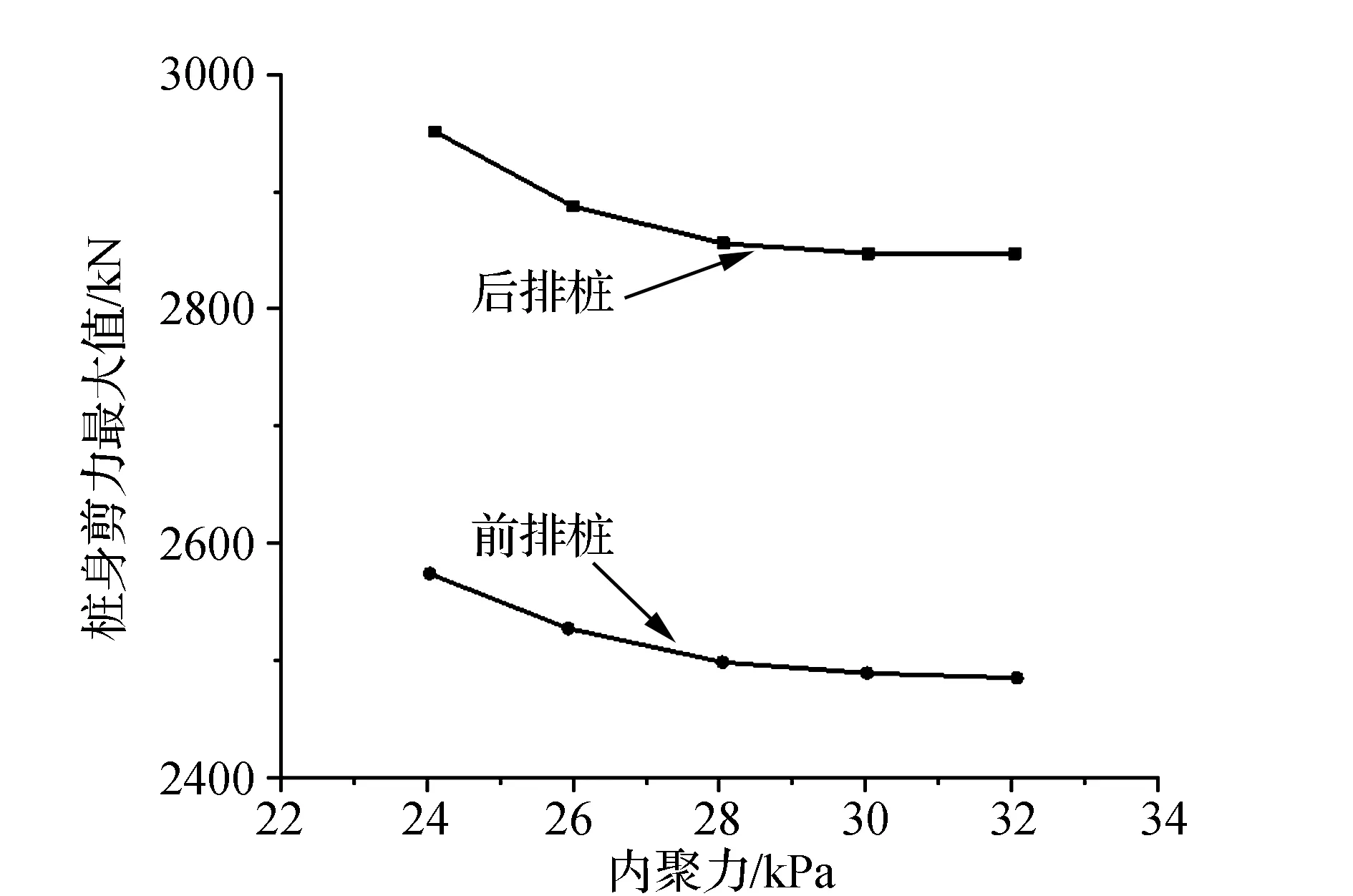
圖6 樁身剪力最大值隨內聚力變化規律
圖7匯總得到抗滑樁承擔滑坡推力隨內聚力變化規律。結果表明,內聚力比較小時,后排樁承擔滑坡推力比例隨內聚力的增大而減小,而前排樁隨內聚力的增大而增大。當內聚力較大時,不同位置抗滑樁承擔滑坡推力比例差異逐漸減小,內聚力大于30 kPa時,兩者比例趨于一致。
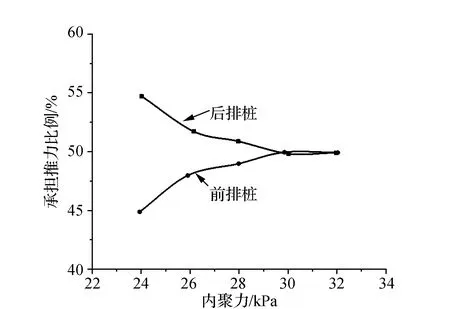
圖7 樁位承擔推力隨內聚力變化規律
2.2 內摩擦角的影響
圖8匯總得到樁頂位移隨內摩擦角變化規律。結果表明,在其他條件不變的情況下,樁頂位移隨內摩擦角的增大而減小,但隨內摩擦角逐漸增大,位移減小速率越來越平緩。也即內摩擦角越小,滑坡推力越大,樁頂位移越大。樁頂位移隨內摩擦角的變化規律與圖2一致。
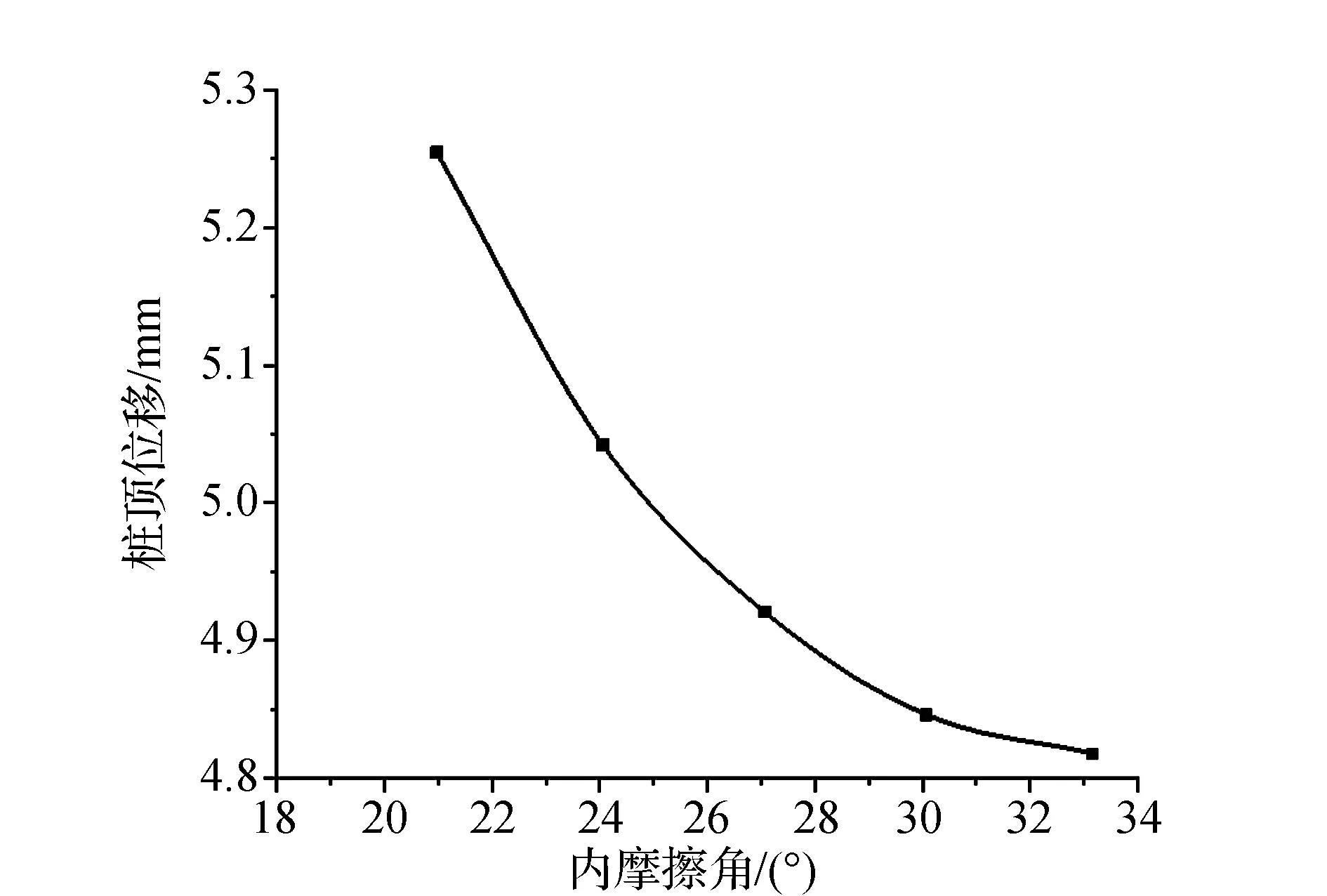
圖8 樁頂位移隨內摩擦角變化規律
圖9匯總得到前排樁和后排樁樁身彎矩隨樁長的變化規律。結果表明,其他條件相同的情況下,內摩擦角對樁身彎矩影響較小。
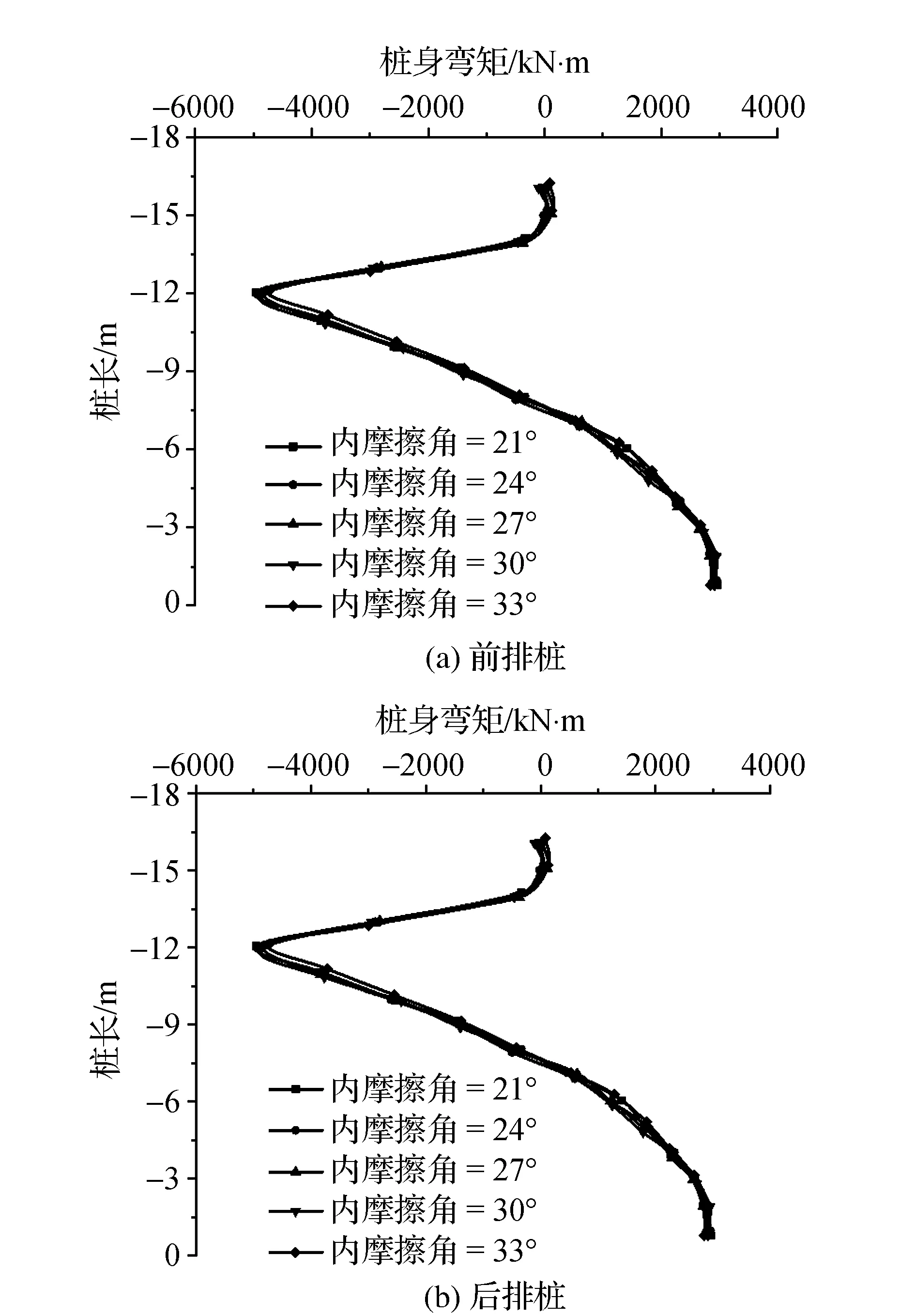
圖9 樁身彎矩隨樁長變化規律
進一步匯總得到樁身最大彎矩隨內聚力變化規律見圖10所示。結果表明,樁身最大彎矩隨內摩擦角的增大而減小。內摩擦角越大,樁身最大彎矩越小,與內聚力對樁身最大彎矩的影響相比,內摩擦角對最大彎矩的影響更為顯著。
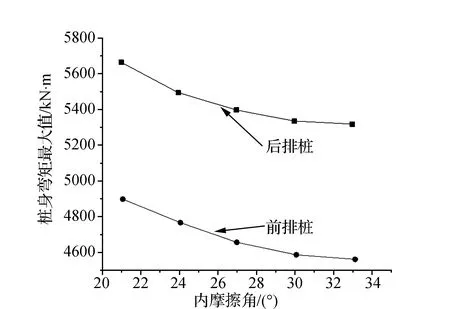
圖10 樁身彎矩最大值隨內摩擦角變化規律
圖11匯總得到前排樁和后排樁樁身剪力隨樁長的變化規律。結果表明,其他條件相同的情況下,內摩擦角對樁身剪力影響較小。剪力最大值出現的位置也基本保持一致。因此,改變土體的內摩擦角不會影響抗滑樁的剪力分布。
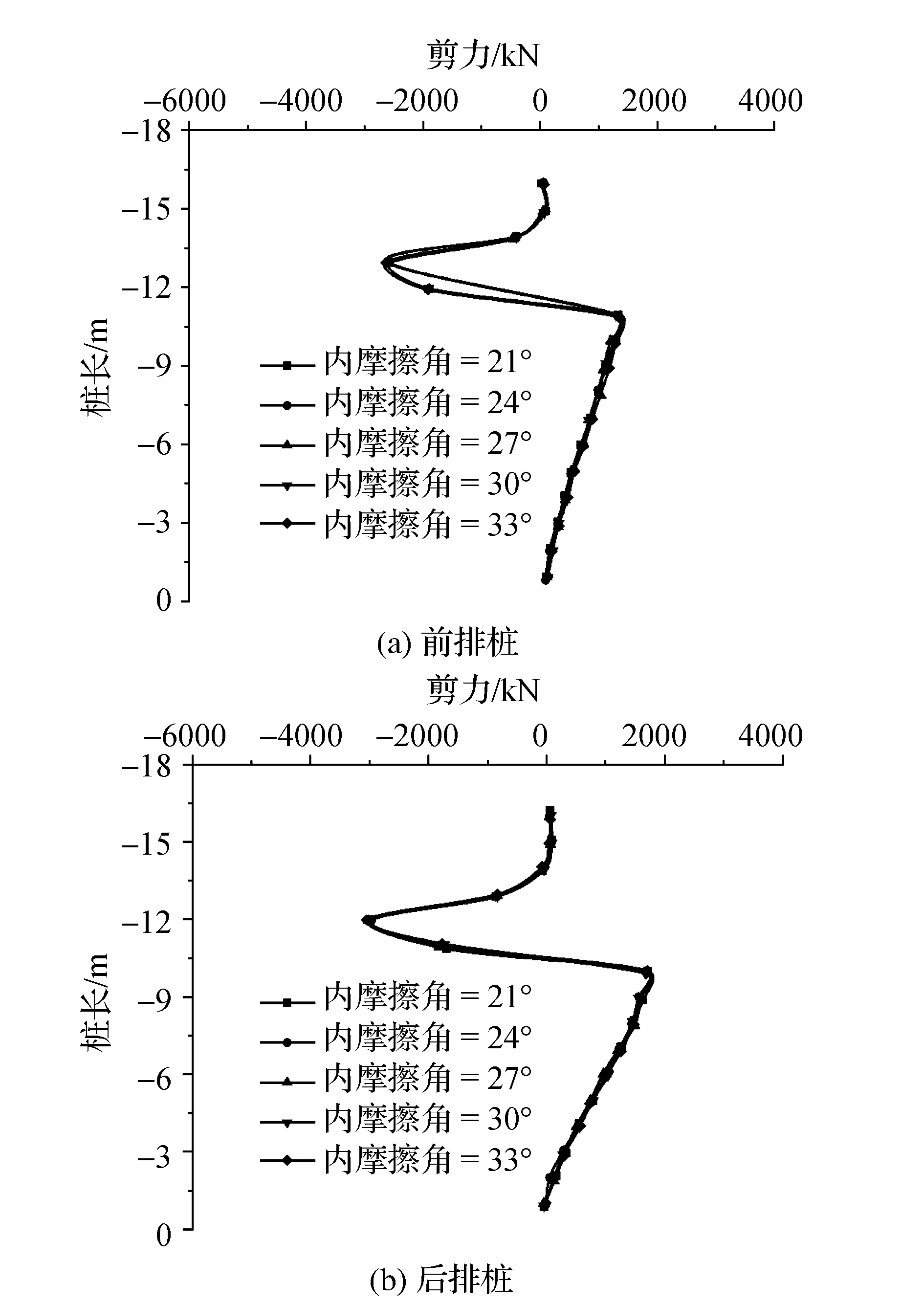
圖11 樁身剪力隨樁長變化規律
進一步匯總得到樁身最大剪力隨內摩擦角變化規律,見圖12所示。結果表明,樁身最大剪力隨內摩擦角的增大而減小。內摩擦角越大,樁身最大剪力越小。
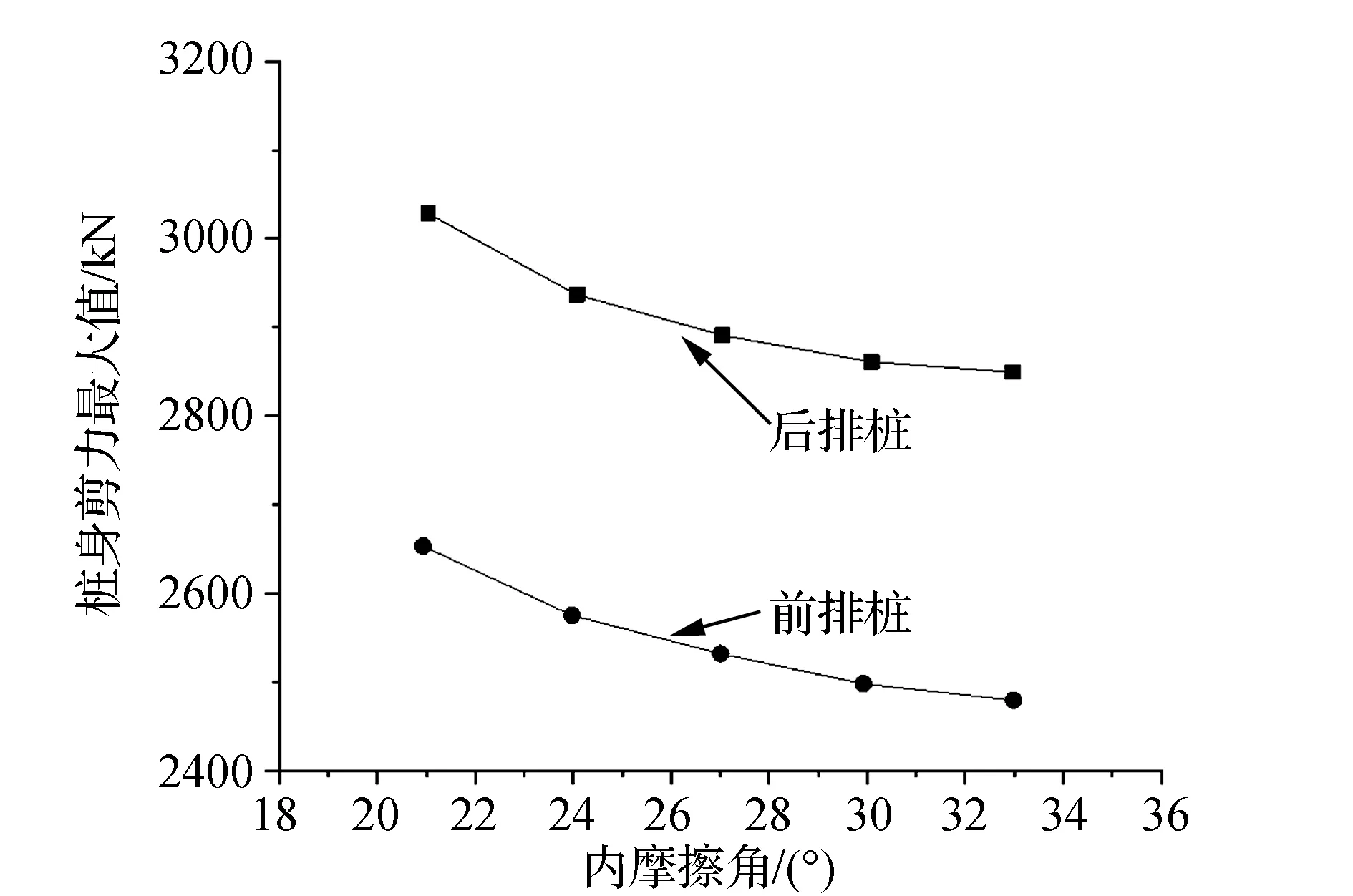
圖12 樁身剪力最大值隨內摩擦角變化規律
圖13匯總得到內摩擦角發生變化時,抗滑樁承擔滑坡推力比例關系。結果表明,當內摩擦角較小時,后排樁承擔滑坡推力的比較逐漸減小,而前排樁承擔的比例逐漸增大,但當內摩擦角為33°時,兩排樁承擔滑坡推力的比例趨于相同。
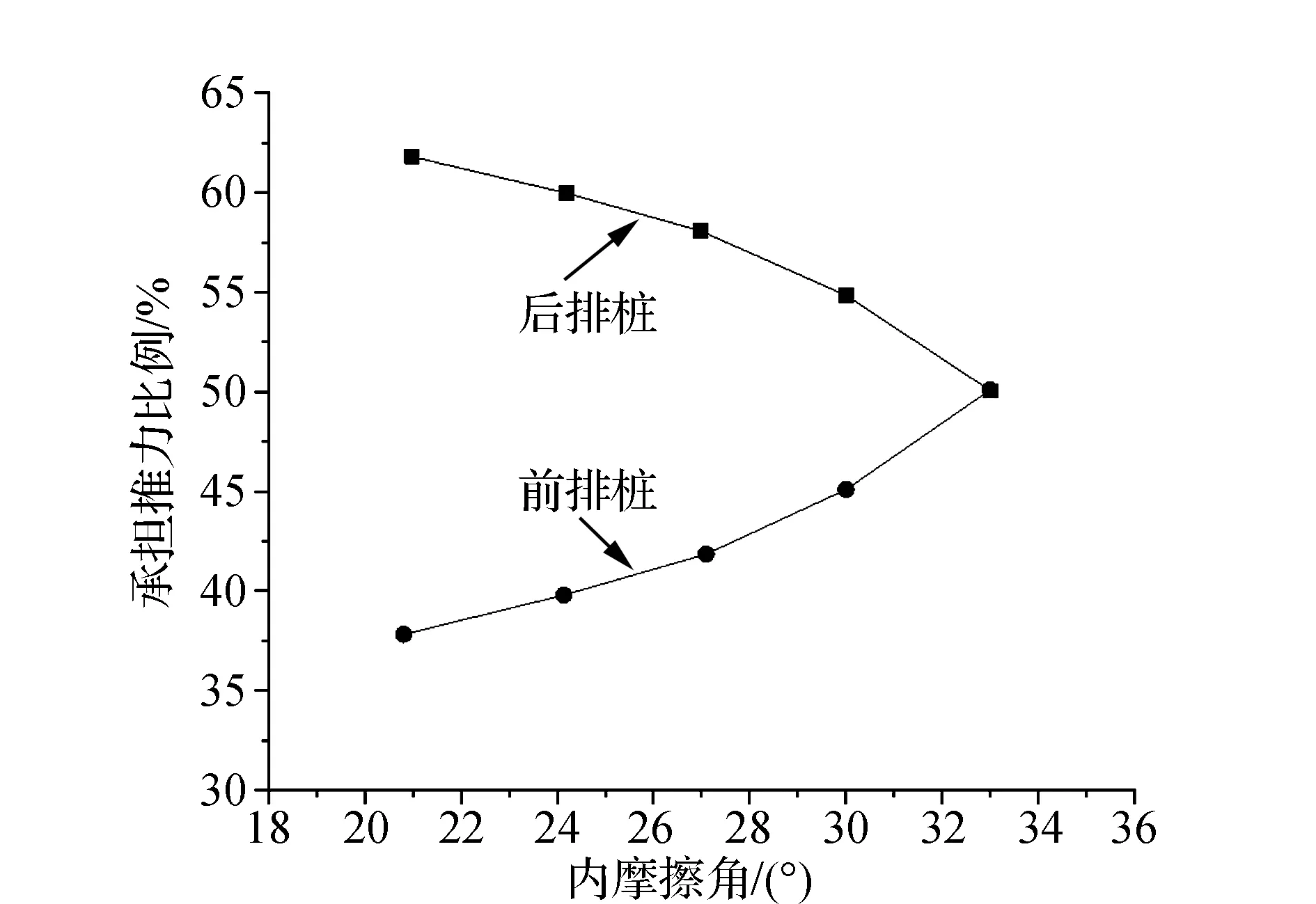
圖13 樁位承擔推力隨內摩擦角變化規律
3 結 論
采用數值有限元研究了土體抗剪強度參數對抗滑樁樁頂位移、樁身彎矩及樁身剪力分布規律s的影響,得到如下結論:
(1)巖土體的抗剪強度參數對抗滑樁的內力分布規律影響不顯著,但會顯著的影響彎矩最大值和剪力最大值。
(2)當土體的強度參數較小時,參數變化對抗滑樁承擔滑坡推力的比例的影響較大,隨著抗剪強度參數的增大,對承擔滑坡推力比例影響越來越小。此外,土體內摩擦角變化對抗滑樁的彎矩和剪力影響幅度比內聚力變化影響更為顯著。

