調頻多普勒引信靜動態干擾信號響應差異性研究

覃 朗,閆曉鵬,代 健

(北京理工大學機電動態控制重點實驗室,北京 100081)

0 引言

在引信抗干擾靜動態等效試驗方法的研究中,需要明晰模擬過程中應考慮的影響因素,以及各種因素的影響程度,才能對干擾信號進行合理設置。為此進行引信靜動態干擾信號響應差異性研究,在內場構造干擾場景以求模擬出真實的外場動態干擾場景,建立引信靜動態干擾信號響應模型。目前的研究中,引信抗干擾靜動態等效試驗方法常常依托經驗,缺乏完整有效的理論支撐。文獻[1—2]通過對正弦調幅干擾信號進行增幅處理的方法得到了引信抗干擾等效試驗實測結果,研究結果表明:在增幅調幅正弦波干擾信號作用下,引信檢波信號具有明顯的增幅特性,能一定程度上模擬出引信動態接近過程中對干擾信號的響應變化。但是該等效試驗方法過于簡單,既沒有考慮引信與干擾機的實際交會場景,也未能獲得引信靜動態條件下對干擾信號的響應變化規律。

調頻多普勒引信由于具有炸點散布小、定距精度高、抗干擾性能好等優點,在常規彈藥中得到廣泛應用[3-4]。文獻[5]研究了調幅干擾對調頻多普勒引信作用機理,研究結果表明:調頻多普勒引信抗正弦波調幅、方波調幅和三角波調幅干擾能力相當;文獻[6]研究了掃頻式干擾對調頻多普勒引信作用機理,研究結果表明:通過合理設置掃頻參數,可以對諧波定距調頻多普勒引信進行干擾。上述研究結果對調頻多普勒引信靜動態抗干擾試驗場景的構造提供了依據,但相關研究均沒有充分考慮引信靜動態干擾信號響應差異性的問題。

本文基于推板試驗實現引信低速運動來構建引信靜態抗干擾試驗場景,設定122 mm 9M22U火箭彈引信受干擾的實際場景來構造引信動態抗干擾試驗場景,并分析對地調頻多普勒引信靜動態條件下對干擾信號的響應規律,進行引信靜動態干擾信號響應差異性研究,為引信抗干擾靜動態等效試驗方法的建立提供技術支撐。

1 調頻引信對典型干擾信號響應特性

典型諧波定距對地調頻多普勒無線電引信的工作原理如圖1所示。圖中m為引信諧波次數,fm為引信調制信號頻率,fd為引信回波信號多普勒頻率。系統工作過程為:經過三角波線性頻率調制的發射信號遇到目標反射后由收發共用天線接收,回波信號與參考調頻信號混頻后輸出包含目標距離信息的差頻信號;差頻信號經過帶通濾波器,濾出包含第m次諧波的中頻信號,然后與預定頻率為mfm的參考信號進行2次混頻和多普勒濾波;輸出的多普勒信號經過信號識別與邏輯判斷后輸出起爆信號。

圖1 調頻多普勒無線電引信原理框圖

以掃頻干擾信號為例,干擾機在對引信進行干擾時,掃頻帶寬通常覆蓋引信的工作頻帶,掃頻信號的載頻會在一定頻率范圍內按一定規律來回擺動。設干擾機的掃頻起始頻率為fj0,掃頻終止頻率為fjN,掃頻步長為Δfj,第n個掃頻點的干擾信號載頻為fjn,掃頻總點數為N+1。則

fjn=fj0+nΔfj,n=0,1,…,N。

(1)

因為干擾機所發射的掃頻干擾信號的載頻是離散變化的,所以引信接收到的干擾信號表達式是一個分段函數,可以將其寫成與門函數相乘的形式。引信所接收到的掃頻式干擾信號可表示為

Sj(t)=[Aj+f(t)]cos(2πfjnt+φjn)gn(t),(n=0,1,…),

(2)

以正弦波調幅掃頻干擾信號為例。掃頻式干擾信號被引信接收后,經過兩次混頻后,對應的多普勒濾波器輸出檢波信號為[6]

(3)

式(3)中,am是引信發射信號的傅里葉系數,A表示引信發射信號幅度,AjM為干擾調制信號幅值,fΔ=fj0-fc為初始頻率差,m表示引信發射信號的諧波次數,m0為諧波定距調頻多普勒引信所選取的定距諧波次數。

2 引信靜動態干擾信號響應差異性

由引信運動引起的瞬時頻率調制:

(4)

式(4)中,fjd是干擾信號到達引信接收機處多普勒頻率,θ是彈-干擾機連線與彈-目連線的夾角,λ是引信工作波長。

由引信和干擾機之間距離和方向系數變化引起的瞬時幅度調制[1-2]:

(5)

式(5)中,k為混頻系數,λ為引信工作波長,D(θ,φ)為引信天線方向性系數,Dj(θ,φ)為干擾機天線方向性系數,φ為方位角(彈目連線與彈-干擾機連線夾角),H為引信-干擾機距離。

可以看出由式(4)、式(5)得到的多普勒信號的幅度和頻率參量包含了引信與目標之間的距離(或者高度)、引信與干擾機的相對運動速度、引信的相對方向系數(天線方向系數和干擾機方向系數)等信息。因此,引信內場靜態對干擾信號的響應和外場動態對干擾信號響應必然會形成顯著差異。而距離和速度是由運動彈道確定的,天線相對方向系數則是由運動彈道和對抗雙方的天線特性共同確定的。對于運動彈道,典型場景下的彈道模型是確定的。對于天線特性,引信和干擾機確定,其相對的方向圖特性也是確定的。以S波段為例,該波段的調頻多普勒無線電引信常采用矩形微帶天線,而在該頻段干擾機多采用喇叭天線[7]。

基于此,本文首先結合典型122 mm 9M22U火箭彈末彈道模型構造動態干擾場景,再構造經過等效縮比的靜態干擾場景,隨后建立引信和干擾機作用模型。接著通過插值的方法,將引信動態場景下得到的受距離變化調制和方向圖相對增益變化調制的檢波信號進行擬合,仿真得到引信動態條件下對干擾信號響應曲線。此外,根據距離與功率衰減關系進行縮比,設置靜態場景等效干擾信號功率實測得到靜態條件下引信對干擾信號的響應曲線。最后,將結果進行對比,可定量得到引信靜動態干擾信號響應差異性。具體流程如圖2所示。

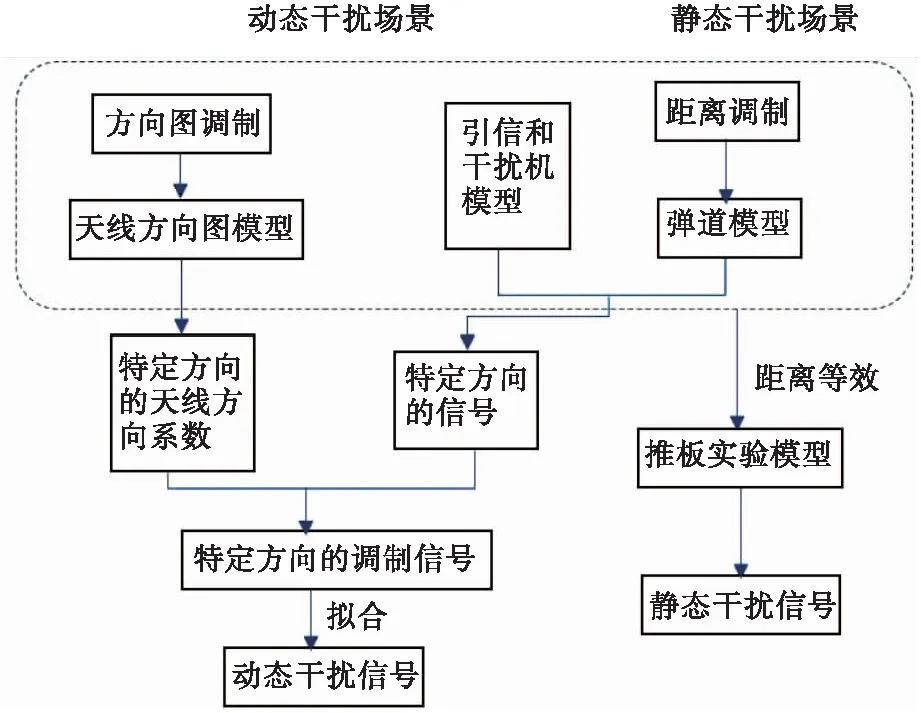
圖2 引信靜動態干擾信號響應差異性分析流程圖

3 試驗驗證分析

3.1 引信動態場景干擾信號響應仿真實驗

建立引信動態干擾場景如圖3所示。其中彈道軌跡仿真距離設為末端1 000 m,干擾機方位設為垂直于彈-目平面距離炮彈落地區100 m的位置,干擾中心設為在x上投影坐標原點800 m左右的位置。以下所有仿真結果水平距離均表示距離彈道起點的橫向距離(在圖3中x軸上投影距離)。

圖3 引信動態干擾場景示意圖

典型122 mm 9M22U火箭彈在發射狀態的仿真參數設置如表1所示[8],結合彈道學典型場景進行仿真,末彈道仿真結果如圖4—圖6所示。

表1 典型火箭彈發射參數

圖4 火箭彈飛行軌跡示意圖

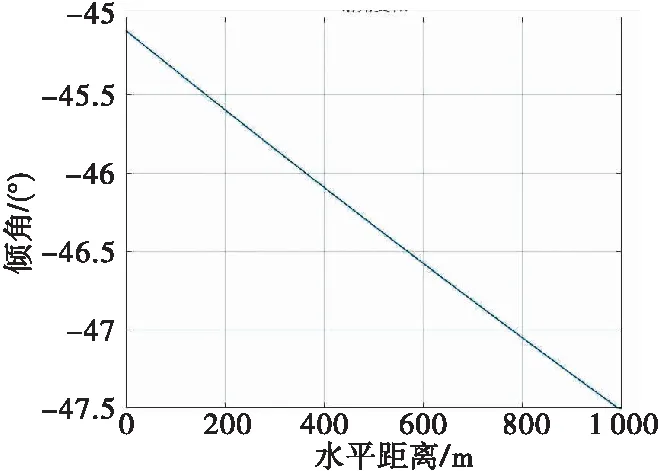
圖5 落角變化示意圖

圖6 速度變化示意圖

由以上仿真數據處理結果可知,火箭彈末彈道飛行軌跡近似為勻速直線運動,速度傾角會有小幅度擺動,其速度呈增大的趨勢。這符合實際發射時122 mm 9M22U火箭彈的變化趨勢[9]。

在建立調頻多普勒引信和干擾信號模型時,引信和干擾信號進行相應參數設置如表2—表3所示[10]。根據圖3所示干擾機與引信對抗場景,參照SPR-2干擾系統的相關性能指標,干擾機的有效輻射功率設置為50 dBm[11-12]。

表2 引信參數

表3 干擾機參數

引信、干擾機模型如圖7—圖8所示。

圖7 三角波調頻多普勒引信模型

圖8 正弦波調幅掃頻式干擾模型

由圖3的布設可以看到,在火箭彈穿越干擾區域時引信具有受干擾機天線旁瓣作用到主瓣作用的過程。引信微帶天線和干擾機用喇叭天線的三維天線方向圖如圖9—圖10所示。圖10喇叭天線波瓣寬度在50°左右,這符合實際使用需求[13]。

圖9 引信微帶天線三維方向圖

圖10 干擾喇叭天線三維方向圖

結合圖5—圖6的火箭彈引信落角、速度與距離關系,可得到特定距離下的天線方向系數,并通過插值的方法,在建立的引信和干擾機作用模型的基礎上,擬合出了引信動態條件下對干擾信號響應曲線,結果如圖11所示[14-15]。可以看到動態干擾場景下,在距離坐標原點600 m之內引信響應的干擾信號較小,但在600 m距離之外的響應信號會急劇增加。形成該結果的原因有兩點:一是引信在初始運動階段和干擾機旁瓣相對,此時方向系數對引信輸出的檢波信號幅度存在較大影響;二是依據雷達方程,引信響應信號幅度隨距離的增加是指數級衰減的。

圖11 引信動態場景下干擾信號響應輸出

3.2 引信靜態場景干擾信號響應試驗

在引信對干擾信號的靜態響應研究中,為了更直觀地對比引信靜動態干擾信號響應差異性,目標與引信移動距離范圍取10 m,速度取4 m/s,這樣得到的引信靜動態干擾信號響應時間幾乎一樣。利用距離與功率衰減關系進行干擾功率設置,靜態干擾場景示意圖如圖12所示。

圖12 引信靜態干擾場景示意圖

采集測試結果,在靜態干擾場景下引信響應干擾信號時檢波輸出信號隨距離變化的結果如圖13所示,可以看到靜態干擾場景下的輸出基本是均勻增大的。

圖13 靜態干擾場景下引信輸出檢波信號

為了更直觀地體現差異性,將靜動態干擾場景下引信響應干擾信號的檢波輸出放在同一時間維度進行觀察,結果如圖14所示。檢波包絡1、2表示在動態和靜態干擾場景下引信響應干擾信號的輸出變化情況。

圖14 靜動態干擾場景下引信輸出檢波信號包絡

可見,在典型122 mm 9M22U火箭彈末端運動的速度范圍內(390～405 m/s),引信在未進入干擾機天線主瓣干擾范圍時(運動的前1.5 s,距離目標水平距離400～1 000 m范圍內),得到的動態干擾信號響應檢波包絡幅度比靜態干擾信號的小1～2個數量級;而在進入干擾機天線主瓣干擾范圍時(運動的1.5～2.5 s,距離目標水平距離0～400 m范圍內),得到的動態干擾信號響應檢波包絡幅度和靜態干擾信號在同一個數量級。因此,在進行引信靜態抗干擾試驗場景構建時應對干擾環境信號進行相應的幅度補償,以逼真的模擬引信動態場景下對干擾信號的響應過程。

4 結論

本文開展了引信抗干擾靜動態等效試驗中的干擾信號響應差異性研究,分析了造成引信靜動態干擾信號響應差異的主要影響因素,獲得了各種影響因素在末彈道不同彈道區間對干擾信號響應的影響程度。本文的研究結果為構造不同場景下的引信抗干擾靜動態等效試驗方法提供了技術支撐。實際情況下還會有許多需要進一步考慮的影響因素,例如干擾機布設方式、天線極化特性等對引信靜動態干擾信號響應的差異性影響,后續將對相關問題進行深入的研究。