4X框架木箱結構內力計算方法研究

黃林峰，滑廣軍，盧富德，肖楚桓，黃益陽

4X框架木箱結構內力計算方法研究

黃林峰1，滑廣軍1，盧富德1，肖楚桓1，黃益陽2*

（1.湖南工業大學，湖南 株洲 412007；2.深圳市冠為科技股份有限公司，廣東 深圳 518110）

以重型包裝運輸用木質框架結構為研究對象，解決木質框架結構內力求解困難的問題。利用解析法，以4X框架結構為例，分別以經驗簡化靜定桁架與無簡化超靜定桁架進行求解；基于ANSYS軟件建立經驗簡化靜定桁架、無簡化超靜定桁架、梁模型、梁桿組合模型及實體模型，并進行對比分析。有限元求解結果與解析法結果具有高度的一致性；經驗簡化靜定桁架的最大軸力超過無簡化超靜定桁架的最大軸力15%；梁模型、梁桿組合模型及實體模型的計算結果與無簡化超靜定桁架的計算結果一致。經驗法對框架結構的簡化往往會導致比較大的誤差，可能導致過包裝設計或欠包裝設計。梁桿組合模型和實體模型建模過程比較復雜，選用梁單元對木箱用框架結構進行數值計算分析，不僅計算精度高，分析處理快捷，而且對復雜工況具有較好的適應性。

重型包裝；框架木箱；力法；超靜定結構；數值仿真分析

重型裝備質量及尺寸規格大，對包裝儲運裝置的強度有較高的要求。目前，木箱仍然是重型裝備儲運的主要形式之一，框架結構是重型木箱的主承載結構，由國家及國際標準指導設計[1]。由于重型裝備結構復雜，重型木箱承載條件惡劣，按照標準設計的木箱結構還需進行驗算[2]。重型木箱框架結構尺寸規格大，對實驗設備要求高，實驗需要將框架和內裝物加工出來才能實施，實驗成本較高，目前驗算的方法主要有解析法和有限元法[3]。木質框架結構一般為超靜定結構，采取解析法計算比較復雜，因此探究高效的數值模擬分析方法，對超靜定木質框架結構的優化設計具有重要意義。

在重型包裝結構的數值模擬分析方面，蔡麗娜等[4]利用ANSYS軟件建立了框架木箱的有限元模型，并進行了靜載、堆碼、叉取、跌落等工況的分析。王海飛等[5]建立了異性截面木塑復合材料托盤的數值模型，并進行了多工況的模擬分析，數值分析結果與實驗測試結果具有高度的一致性。石軍鍵等[6]對非標設計的鋼木組合箱進行了數值建模分析，基于多工況對鋼木組合箱進行了優化。沈仙法等[7]基于ANSYS軟件對木箱的枕木和縱梁構件進行了輕量化設計。邱鵬飛等[8]采用有限元軟件分析了包裝箱底座的承載能力，基于結構整體應力分布及變形，對結構進行了改進設計。衛佩行等[9]利用ANSYS軟件研究了汽輪機產品用木框架包裝箱的力學性能，為改進框架式包裝箱提供了依據。在對框架結構的解析法分析方面，彭國勛等[10]將4X框架結構簡化為桁架，并將其中的8根桿作為零力桿來處理，獲得了靜定的桁架結構，并采取解析方法獲得了各桿的內力。郭長城[11]將1X框架作為超靜定桁架結構進行解析求解，分析表明，1X框架中沒有零力桿。隋允康等[12]以超靜定桁架為研究背景，利用其結構特性提高了自適應結構的承載能力。邊文鳳等[13]提出了微分解析法以求解高次超靜定桁架的變形協調方程問題。吳曉[14]采用構造拉格朗日函數法研究了超靜定工程結構的內力求解，結合算例分析表明，該方法通用性強，且無須補充變形協調方程。

為準確把握木質框架結構的承載狀態，本文以框架木箱中使用的4X框架結構為例，采取解析法，分別以簡化靜定桁架結構、無簡化超靜定桁架結構為對象進行理論求解。基于ANSYS仿真平臺，分別建立簡化靜定桁架結構模型、無簡化超靜定桁架模型、無簡化梁模型、梁桿組合模型、實體模型。對解析結果與數值計算結果進行對比分析，給出木質框架結構內力分析方法的建議，為復雜超靜定木質框架結構準確、高效的設計提供支撐。

1 木箱用框架結構特點

包裝用框架木箱的側面通常由框架和箱板組成，如圖1所示。框架由上框木、下框木、立柱和斜撐等構件組成，一般采用鋼釘或螺栓連接，典型的框架結構形式主要有：無斜撐結構、N、X、K、HK、XX、KK、KKK形框架等[1]。框架結構的承載狀態與框架的結構形式、載荷形式有關。以圖2所示的4X框架為例，當兩端起吊，底部3個節點承受載荷時，立柱、斜撐、上框木、下框木承受的載荷都是沿著構件軸線方向，可以簡化為桁架結構。更普遍的工況是產品的重量通過枕木作用在滑木和下框木組成的組合梁上，如果枕木沒有布置在立柱與下框木連接部位，或起吊點不在構件的連接節點上，則組合梁會承受垂直軸向的載荷，此時不能用桿件來近似。因此，該4X框架只有在特殊承載條件下才能簡化為桁架結構，而更普遍的情況則應該用梁構件進行表征。對木箱結構進行工程分析，雖然可以選用實體單元對結構的承載狀態進行表征，但重型包裝用的木質框架并非精加工結構，各構件之間的接觸狀態難以準確模擬。下面分別基于解析法和不同類型的數值模擬方法進行對比分析，為包裝用框架結構準確、高效的分析方法的選擇提供依據。

圖1 側面框架結構

2 木質框架結構內力的解析解

對于靜定桁架，一般采取節點法或截面法求解各桿內力。對于超靜定桁架，一般采取力法或位移法求解，這2種方法的求解思路都是將未知超靜定結構問題轉換成已知的靜定結構問題，轉換的橋梁是基本體系，轉換的條件是基本方程，要解決的關鍵問題是求解基本未知量[11]。其中，力法是以多余未知力為基本未知量、一般用靜定結構作為基本結構，基于變形協調條件建立基本方程，最后求解超靜定結構內力[15]。

2.1 經驗簡化桁架模型解析法

對于復雜桁架結構，一般根據經驗確定零力桿，去掉零力桿后得到靜定結構，然后利用節點法或截面法進行求解。對于圖2所示4X木質框架，若各桿截面積均為、框架高度為、各橫跨間距為、外載荷為、木材彈性模量為、泊松比，計算各桿軸向力a。按照文獻[10]，將該4X結構中的8根桿作為零力桿處理，去掉零力桿的結構如圖3所示。其中，點與點的支反力為1.5，方向向上。利用力平衡方程從點開始，按照方程組（1）可逐點求解圖3各桿軸力。

圖2 4X平面桁架

Fig.2 4X plane truss

圖3 去除零力桿后的4X平面桁架

2.2 無簡化桁架模型解析法

對于圖2框架結構，根據文獻[11]可知，此類型的桁架結構屬于超靜定結構，可以按照力法建立變形協調方程進行求解。

用力法求解超靜定結構時，首先要確定超靜定次數。切斷超靜定結構的一根桁架桿會暴露出一個靜不定力，相當于去掉一個多余聯系。圖2所示結構切斷桿、桿、桿、桿后化為靜定體系，見圖4，則原結構的超靜定次數等于4。

圖4 4X框架基本結構

取基本結構如圖4所示。有4個變形條件：

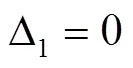
其展開式為：

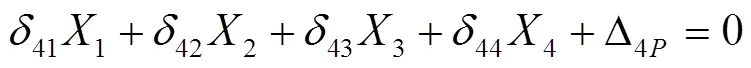
式（6）分別表示基本結構的5桿、6桿、7桿、8桿截口兩側截面無相對位移。基本結構的位移是由桿件軸向變形引起的，則典型方程中的系數和常數項按式（4）計算。

3 木質框架結構內力的解析法應用實例

圖2所示的4X木質框架中，各桿截面積為0.002 5 m2、框架高度為1 m、橫跨間距為1 m、外載荷=10 000 N、木材彈性模量為10 GPa、泊松比為0.3，計算各桿軸向力a。利用方程組（1）從點開始，可求解圖3各桿件的軸力a，結果如表1所示，其中桿件2、桿件3承受的最大拉力為20 000 N，桿件10、桿件20承受最大壓力為21 210 N。按照超靜定桁架結構內力求解方法，可得該4X框架無簡化桁架模型的解析解。無簡化桁架模型的解析解表明，該4X框架結構沒有零力桿，桿2、桿3承受的最大拉力為16 530 N，桿6、桿7承受的最大壓力為18 470 N。

表1 框架軸力

Tab.1 Axial force of frame N

4 木質框架結構內力的有限元分析

從木質框架結構特征來分析，在實際工程應用時，圖2所示結構的上部4個構件和下部4個構件往往選擇一根整體材料，承載點一般也不在立柱與下框木連結部位，因此圖2所示桁架是木質框架結構的簡化特例，簡化往往會導致較大的誤差（表1的解析解已經表明）。本研究基于ANSYS仿真平臺，分別建立了圖3所示的經驗簡化靜定桁架模型、圖2所示的無簡化超靜定桁架模型、無簡化梁模型、梁桿組合模型和實體模型，并對各構件的內力進行了對比分析。

4.1 經驗簡化桁架模型解析法

在ANSYS的Mechanical APDL工作環境，選擇Link180單元，定義桿截面為0.002 5 m2，定義材料屬性=10 GPa，泊松比為0.3。先輸入坐標定義節點，再通過節點創建單元，建立圖3所示桁架的有限元模型，并在、、點施加載荷，在、點施加約束，創建完畢的有限元模型如圖5所示。執行求解后，軸力如圖6所示，其中底部4根桿和3根立柱承受拉力，頂部2根桿和4根斜撐承受壓力。定義單元表（Element Table）各單元軸向力，提取單元表數據得到各桿軸力，如表1所示。

4.2 無簡化桁架模型數值分析

按照圖2在ANSYS的Mechanical APDL工作環境構建無簡化桁架結構有限元模型，單元選擇、材料定義、桿單元節點定義、載荷及約束施加方法與4.1節相同。執行求解后，軸力圖如圖7所示，其中底部4根桿和中間3根立柱承受拉力，頂部4根桿和兩端立柱承受壓力，各桿的軸力如表1所示。由表1中無簡化桁架模型計算結果可知，解析解與數值解一致，圖2中的框架結構中并沒有真正的零力桿。

圖5 經驗簡化桁架模型

圖6 經驗簡化桁架模型軸力

圖7 無簡化桁架模型軸力

4.3 無簡化梁模型數值分析

對于圖2所示的4X框架結構，當非節點部位承受橫向載荷時，下部結構用桿結構進行簡化則會造成較大的誤差，因此考慮基于梁模型描述4X框架的承載狀態。在ANSYS的Mechanical APDL工作環境下，單元選擇Beam188單元，梁截面定義為面積為0.002 5 m2的正方形。材料定義、梁單元節點定義、載荷及約束施加方法與4.1節相同。建模過程仍然采取直接建模法，先建節點，再建單元，計算結果如圖8所示，無簡化梁模型計算各構件的承載狀態與無簡化桁架模型的相同。具體各構件的承載力如表1所示，因此，對于圖2的特殊工況條件，采取梁模型的分析結果與采取桿模型的分析結果高度一致。當底部構件在非連接點部位承受非軸向載荷時，采用梁模型進行分析更加方便。

圖8 無簡化梁模型軸力

4.4 桁架和梁組合模型有限元分析

當圖2所示的4X框架結構用于框架木箱時，用梁模擬上框木和下框木更有普遍性。在使用過程中，斜撐和立柱很少受到非軸向載荷，因此用桿進行模擬是合理的。綜合考慮用梁桿混合模型對圖2的4X木質框架結構進行模擬，對上部4個構件和下部4個構件采用梁單元建模，對斜撐和立柱采用桿單元建模，形成組合結構模型。建模過程、材料特性、構件截面參數、載荷及約束與4.1節及4.2節相同。計算結果如圖9所示，各構件的承載狀態與無簡化梁模型相同，軸力數值相差僅在1.6%以內。具體各構件的承載力如表1所示。

圖9 梁與桿組合模型軸力

4.5 實體模型有限元分析

對圖2所示的木制框架結構在ANSYS Workbench工作環境中用實體單元構建有限元模型，與之前的模型進行對比和分析。先在三維設計軟件繪制0.05 m×0.05 m的矩形橫截面框架木箱側面結構實體模型，將其導入Workbench中生成有限元模型。材料定義與4.1節相同，構件之間的接觸類型定義為Bonded。選擇下框木左部底邊棱，施加、、3個方向的平動約束；選擇下框木右部底邊棱，施加、2個方向的平動約束，提取第一主應力以及各構件內力。執行求解后，應力如圖10所示。在受約束部位出現應力奇異現象，該處的應力值過大且不收斂。根據圣維南原理可知，在離約束端稍遠處的模型內部的應力值依舊是準確的。由表1可見，各構件的受力狀況與圖7、圖8、圖9基本一致，但相比于桿單元、梁單元和混合單元，實體單元模型的仿真結果與解析解差距較大。其中14號桿的仿真結果與解析解相差約15%。

圖10 實體模型應力

5 結語

以4X型木質框架為例，分別采取解析法及5種有限元模型進行分析，計算了各構件的承載力。通過分析得到以下結論：

1）對于經驗簡化桁架模型，采取解析法的計算結果與有限元法的計算結果具有高度的一致性，但經驗簡化桁架模型的最大軸力比無簡化桁架模型中的最大軸力大15%左右，因此經驗簡化會放大結構的承載狀態，對框架木箱的設計不利。

2）無簡化桁架模型、無簡化梁模型、梁桿混合模型及實體模型計算結果表明，框架木箱使用的4X型框架結構中沒有零力桿，采取經驗法常常會出現誤判的現象。有限元數值分析方法能夠避免經驗判定造成的誤差，同時避免了采用解析法求解超靜定結構的大量人工計算。

3）梁模型的計算結果與桁架模型的計算結果一致，誤差小于1%。桁架模型只能分析節點受軸向載荷的特殊工況，而梁模型能夠分析更普遍的工況，也能夠避免經驗法造成的誤判。因此對于重型包裝中的木質框架結構，采用梁模型進行數值模擬分析，是一種高效、精確、適應性好的分析方法。

4）實體模型、梁桿混合模型的計算結果與超靜定桁架模型、梁模型的計算結果具有高度的一致性，誤差小于1.6%。梁桿混合模型的建模較復雜，需要對不同單元的節點進行耦合處理。實體單元建模過程中各構件之間的接觸類型較難確定。本文采用的Bonded接觸不允許接觸面之間存在法向分離和切向滑移，接觸剛度大，用它來模擬木框架構件之間的接觸狀態會產生一定的誤差，且計算時容易在幾何約束部位與載荷施加部位產生應力奇異，影響對結構承載狀態的準確評價，分析效率低。

5）綜合分析認為，基于ANSYS協同仿真平臺，選用梁單元對木箱用框架結構進行數值計算分析，不僅計算精度高，分析處理快捷，同時對復雜工況具有較好的適應性。

[1] GB/T 7284—2016, 框架木箱[S].

GB/T 7284—2016, Wooden Framed Case[S].

[2] 彭國勛. 機電產品木包裝系統設計[M]. 北京: 印刷工業出版社, 2014: 282-283.

PENG Guo-xun. Wood Packing System Design with Mechatronics Products[M]. Beijing: Printing Industry Press, 2014: 282-283.

[3] 滑廣軍, 易穎茵, 肖建, 等. 基于Ansys的重型包裝鋼架箱工程輕量化設計[J]. 包裝工程, 2022, 43(3): 183-188.

HUA Guang-jun, YI Ying-yin, XIAO Jian, et al. Engineering Lightweight Design of Steel Frame Box for Heavy-Duty Packaging Based on Ansys[J]. Packaging Engineering, 2022, 43(3): 183-188.

[4] 蔡麗娜, 王玉龍, 徐潔, 等. 框架木箱有限元受力分析[J]. 包裝工程, 2010, 31(17): 13-15.

CAI Li-na, WANG Yu-long, XU Jie, et al. Finite Element Analysis to Stress of Wooden Framed Box[J]. Packaging Engineering, 2010, 31(17): 13-15.

[5] 王海飛, 滑廣軍, 郭亞飛, 等. 異形截面木塑復合材料托盤的數值模擬與實驗對比分析[J]. 包裝學報, 2019, 11(2): 8-13.

WANG Hai-fei, HUA Guang-jun, GUO Ya-fei, et al. Numerical Simulation and Experimental Analysis of Wood Plastic Composite Pallet with Irregular Section[J]. Packaging Journal, 2019, 11(2): 8-13.

[6] 石軍鍵, 李光. 不同工況下鋼架木箱有限元分析及優化設計[J]. 包裝與食品機械, 2016, 34(2): 37-40.

SHI Jun-jian, LI Guang. Finite Element Analysis and Optimization Design on Steel Frame Wooden Cases under Different Working Conditions[J]. Packaging and Food Machinery, 2016, 34(2): 37-40.

[7] 沈仙法, 崔小龍. 基于Ansys Workbench的機電產品木質包裝箱的結構優化[J]. 包裝工程, 2020, 41(13): 104-110.

SHEN Xian-fa, CUI Xiao-long. Structural Optimization of Wood Packaging Boxes for Mechanical and Electrical Products Based on Ansys Workbench[J]. Packaging Engineering, 2020, 41(13): 104-110.

[8] 邱鵬飛, 王泉中, 蔣身學. 基于ansys的大型機電產品包裝箱底架有限元分析[J]. 木材加工機械, 2014, 25(1): 45-48.

QIU Peng-fei, WANG Quan-zhong, JIANG Shen-xue. Finite Element Analysis of Packing Based on ANSYS of Large Electromechanical Products[J]. Wood Processing Machinery, 2014, 25(1): 45-48.

[9] 衛佩行, 饒鑫, 王泉中, 等. 基于ANSYS的機電產品框架型包裝箱有限元分析[J]. 木材加工機械, 2014, 25(4): 9-12.

WEI Pei-xing, RAO Xin, WANG Quan-zhong, et al. Finite Analysis of the Electromechanical Packing Container by Ansys Software[J]. Wood Processing Machinery, 2014, 25(4): 9-12.

[10] 彭國勛. 物流運輸包裝設計[M]. 2版. 北京: 印刷工業出版社, 2012: 194-198.

PENG Guo-xun. Logistics Transportation Packaging Design[M]. 2nd ed. Printing Industry Press, 2012: 194-198.

[11] 郭長城. 結構力學[M]. 武漢: 武漢大學出版社, 2000: 163-164.

GUO Chang-cheng. Structural Mechanics[M]. Wuhan: Wuhan University Press, 2000: 163-164.

[12] 隋允康, 邵建義. 自適應超靜定桁架結構強度控制的研究[J]. 固體力學學報, 2001, 22(2): 136-142.

SUI Yun-kang, SHAO Jian-yi. Research on Strength Control for Adaptive Structure of Statically Indeterminate Truss[J]. Acta Mechanica Solida Sinica, 2001, 22(2): 136-142.

[13] 邊文鳳, 董正筑. 超靜定桁架變形協調方程的新方法[J]. 計算力學學報, 2002, 19(2): 250-252.

BIAN Wen-feng, DONG Zheng-zhu. A New Method for Problem of Hyperstatic Truss[J]. Chinese Journal of Computational Mechanics, 2002, 19(2): 250-252.

[14] 吳曉. 求解工程中靜不定結構內力的通用方法[J]. 中南大學學報(自然科學版), 2016, 47(1): 262-272.

WU Xiao. A General Method of Solutions for Engineering Statically Indeterminate Structure Force[J]. Journal of Central South University (Science and Technology), 2016, 47(1): 262-272.

[15] 劉鴻文. 材料力學Ⅱ[M]. 高等教育出版社, 2017: 129-132.

LIU Hong-wen. Mechanics of Materials II[M]. Higher Education Press, 2017: 129-132.

Internal Force Calculation Method of Wooden Box Structure with 4X Frame

HUANG Lin-feng1, HUA Guang-jun1, LU Fu-de1, XIAO Chu-huan1, HUANG Yi-yang2*

(1. Hunan University of Technology, Hunan Zhuzhou 412007, China; 2. Shenzhen Glareway Technology Co., Ltd., Guangdong Shenzhen 518110, China)

The work aims to propose a solution method of the internal force of the wooden frame structure by taking the wooden frame structure for heavy-duty packaging and transportation as the research object. With 4X frame structure as an example, the empirical simplified statically determinate truss and non-simplified statically indeterminate truss were theoretically solved by analytical method. Based on ANSYS software, empirical simplified statically determinate truss, non-simplified statically indeterminate truss, beam model, beam and rod combination model and solid model were established respectively, and comparative analysis was carried out. The results of finite element analysis were highly consistent with those of analytical method. The maximum axial force of empirically simplified statically determinate truss exceeded the maximum axial force of non-simplified statically indeterminate truss by 15%. The calculation results of beam model, beam and rod combination model and solid model were highly consistent with those of the non-simplified statically indeterminate truss. The simplification of frame structure by empirical method often leads to large errors, resulting in over packaging design or under packaging design. The modeling process of beam and rod combination model and solid model is relatively complex. The beam element is selected for numerical calculation and analysis of the frame structure for wooden box, which not only has high calculation accuracy and fast analysis processing, but also has good adaptability to complex working conditions.

heavy-duty packaging; framed wooden box; force method; statically indeterminate structure; numerical simulation analysis

TB485.3

A

1001-3563(2023)17-0167-07

10.19554/j.cnki.1001-3563.2023.17.020

2023-03-11

湖南省教育廳重點科研項目（21A0353，22A0397）；湖南省自然科學基金（2022JJ30223）；湖南省高等學校教學改革研究（HNJG-2021-0123，HNJG-2021-0704）；國家級大學生創新創業訓練計劃項目（202111535014）

責任編輯：曾鈺嬋