剛性彈侵徹/貫穿混凝土靶體的工程實用化計算模型*

洪智捷，楊耀宗，孔祥振，方 秦

（陸軍工程大學爆炸沖擊防災減災國家重點實驗室，江蘇 南京 210007）

隨著常規武器的迅速發展，鉆地彈的命中精度和侵徹能力均有了較大提高，對我國重要軍事工程及關鍵基礎設施帶來了嚴峻威脅。準確計算鉆地彈的侵徹破壞效應是工程防護設計的基礎，也是防護工程領域關心的熱點問題。

鉆地彈對混凝土材料的侵徹深度是工程防護設計關注的首要問題。針對該問題，國內外學者進行了大量的研究工作，建立了侵徹深度的預測公式，主要可分為兩類。一類是以理論模型為基礎確定彈體侵徹過程中靶體阻力函數，然后通過試驗數據確定或修正相關系數，最終得到預測侵徹深度的半解析模型，如空腔膨脹模型[1-3]、速度場模型[4]等。上述理論模型雖然能較好描述侵徹過程中的關鍵物理機制，但一般形式較為復雜，不便于工程應用，且大部分模型是通過小口徑縮比彈試驗進行擬合和驗證的，因此是否能推廣到大口徑原型彈值得商榷。另外一類是目前在防護工程設計中廣泛使用的經驗公式。當前國內外有關鉆地彈對介質侵徹深度的計算公式有幾十種，但是隨著鉆地彈武器的發展，新型鉆地彈具有彈頭尖銳、長徑比大等特點，因此上述經驗公式的適用性和準確性還有待進一步驗證。Li 等[5]、王安寶等[6]、張爽[7]和程月華等[8]從公式形式、適用范圍和預測精度對已有侵徹深度的經驗公式進行了較為全面的評述，主要有兩個結論：一是經驗公式形式簡單，但量綱不協調，經驗系數無明顯物理意義；二是不同的經驗公式往往只適用于特定的彈頭形狀、質量以及靶體強度，尺寸效應突出導致多數經驗公式對大口徑鉆地彈的預測精度較差，難以為防護設計提供可靠參考。因此，目前仍缺乏具有一定物理基礎、預測精度較高且形式簡單的新型鉆地彈侵徹深度的工程實用化計算模型。

靶體的侵徹不貫穿厚度（或臨界貫穿厚度）是防護工程設計關注的另外一個主要問題，可為遮彈層設計提供參考。現有臨界貫穿厚度的公式形式都較為簡單，大多通過對試驗數據直接擬合得到。龔自明等[9]通過開展貫穿試驗，得到鋼筋混凝土的臨界不貫穿厚度為1.3 倍的侵徹深度；修正的Petry 公式[10]中臨界貫穿厚度為侵徹深度的2 倍；而ACE 公式[11]和NDRC 公式[12]中的臨界貫穿厚度則與侵徹深度呈簡單的一次關系式。這些取值或關系式都缺乏理論基礎，因此可能導致對臨界貫穿厚度的預測誤差較大。Li 等[13]和Chen 等[14-15]基于試驗現象提出了彈體貫穿混凝土的三階段模型，并認為臨界貫穿厚度應等于彈體侵徹深度和靶背沖塞塊高度之和，同時給出了計算沖塞塊高度的計算公式，但缺乏足夠的試驗數據對該公式進行驗證。Peng 等[16]基于對貫穿試驗后坑高度的試驗數據分析，認為厚靶沖塞塊高度約為2.5 倍的彈徑，而薄靶則約為0.5 倍靶體厚度，但缺乏一定的理論依據。因此，目前仍缺乏考慮彈體及靶體材料性質的臨界貫穿厚度的工程實用化計算模型。

為解決上述問題，本文中基于對剛性彈侵徹貫穿混凝土靶體的阻力和過程分析，分別建立相關的計算模型，給出侵徹深度和臨界貫穿厚度的工程實用化計算公式，并通過145 組侵徹試驗和32 組貫穿試驗數據對計算模型進行了驗證。

1 剛性彈侵徹混凝土靶體的計算模型

首先對剛性彈侵徹混凝土靶體的阻力進行分析，提出線性上升-恒定的兩階段阻力模型，并基于此建立侵徹深度的計算公式；然后基于大量試驗數據，通過引入彈徑修正系數提高計算公式的預測精度；最后基于大口徑、大長徑比的彈體侵徹試驗數據，驗證提出公式的可靠性。

1.1 侵徹阻力

剛性彈侵徹過程中，彈體所受阻力是建立侵徹深度計算模型的基礎。基于空腔膨脹模型，Forrestal 等[17]、Chen 等[18]給出剛性彈侵徹阻力F的一般形式為：

式中：d為彈徑，fc為靶體單軸壓縮強度，ρ 為靶體密度，A和B為與靶體材料相關的常數，v為侵徹過程中彈體瞬時速度，N1和N2為與彈頭幾何形狀及彈靶摩擦相關的無量綱數。從式（1）可看出，彈體所受阻力由兩部分組成：一是準靜態阻力項，主要與材料強度相關；二是動態阻力項（慣性項），主要與速度相關。

注意到式（1）為侵徹穩定階段的彈體阻力（彈體加速度），而實際侵徹過程中彈體加速度的變化較為復雜。Forrestal 等[19]、Rosenberg 等[20-23]、Yankelevsky 等[24-25]、陳小偉等[26]和Kong 等[2,27]針對上述問題提出了不同的觀點。Forrestal 等[19]基于彈載加速度試驗數據，發現彈體加速度分為兩個階段：第一階段為線性上升段，對應于侵徹的初始階段；第二階段為緩慢下降的平臺段，對應于侵徹的隧道階段。Rosenberg 等[20-23]通過開展彈體侵徹金屬靶體的二維數值模擬，發現彈體侵徹金屬靶體的加速度幾乎為一個定值，進一步結合彈體侵徹混凝土靶體的試驗數據，認為恒定加速度的模型可以推廣到混凝土靶體中，并忽略了彈體侵徹過程中初始階段加速度的變化（圖1 中橘色線）。但是陳小偉等[26]認為速度較低時，慣性項影響可忽略；而當速度較高時，慣性項和材料強度項相當，不可忽略。Yankelevsky等[24]也指出，恒定加速度模型沒有物理意義，認為Forrestal 等[19]提出的兩階段侵徹阻力模型（圖1 紅線）較為可靠，并在此基礎上提出了改進的二階段加速度線性下降模型（圖1中綠線）。Kong 等[27]與Forrestal 等[19]、陳小偉等[26]和Yankelevsky 等[24]的看法相似，即隧道階段的彈體加速度與速度相關，只是在低速情況下動態阻力項的貢獻較小。

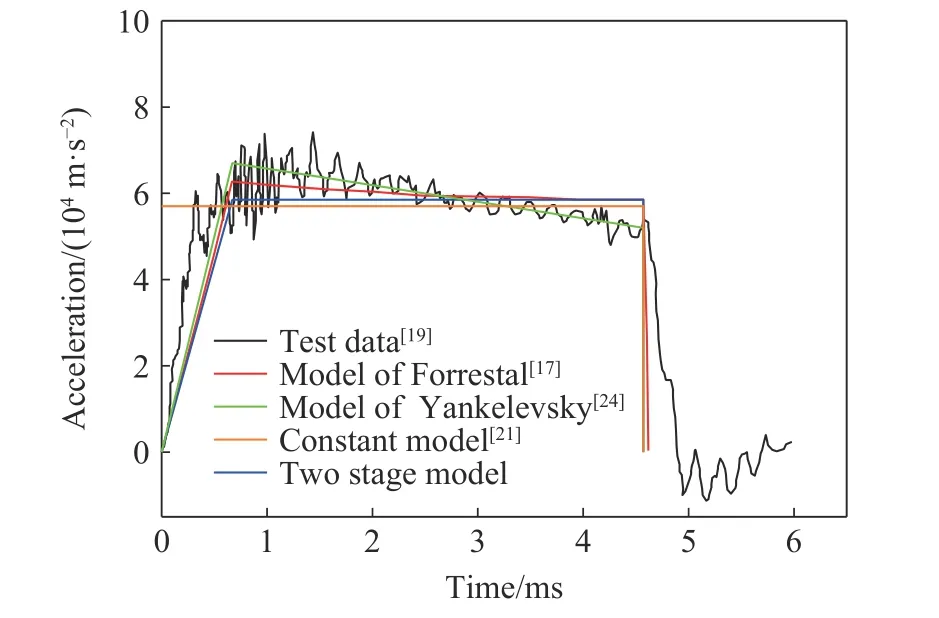
圖1 彈體加速度時程曲線Fig.1 Acceleration-time history curves of projectile

綜上所述，針對剛性彈侵徹混凝土靶體過程中的侵徹阻力/彈體加速度主要存在以下兩點爭議，一是初始階段侵徹阻力的變化是否需考慮，二是隧道階段侵徹阻力中的慣性項是否需考慮。首先，本文主要研究的是淺侵徹問題，因此初始階段的侵徹阻力變化不可忽略。其次，根據Forrestal 等[19]和Frew 等[28]開展的混凝土侵徹試驗發現在其試驗速度范圍內（＜460 m/s）慣性項的影響非常小，Rosenberg 等[20]也對Frew 等[29]開展的小直徑尖卵形剛性彈侵徹混凝土靶體試驗開展分析，發現在400～1 200 m/s 范圍內，慣性項的影響同樣可忽略。而鉆地彈著靶速度通常不超過400 m/s，因此為便于解決工程問題，隧道區采用恒定阻力（即不考慮慣性項）是合理的，這也與Peng 等[16]提出的平均阻力模型一致，因此可采用線性上升-恒定的兩階段侵徹阻力模型，如圖1 中藍色實線所示。

目前針對上述兩階段的界限仍存在分歧，Forrestal 等[1]和Chen 等[18]認為混凝土靶體的開坑深度即為初始階段的侵入深度，同時分別假定開坑深度為2d和0.707d+l（l為彈頭長度）。而Teland 等[30]假設尖卵形彈體侵徹過程中彈體受力面積近似線性增加，因此認為初始階段侵徹阻力線性上升。圖2 則給出了尖卵形彈體侵入混凝土靶體的高速攝像[29]，從圖中可以看出彈體頭部侵入靶體后，混凝土仍未產生飛濺，因此認為侵徹阻力隨著受力面積增加而線性上升的描述是合理的。故本文中采用Teland 等[30]的假設，即認為初始階段侵徹深度為彈頭長度l，同時忽略彈靶界面的摩擦效應，則侵徹阻力表達式為：

圖2 彈體侵入混凝土靶體圖像[31]Fig.2 Photograph of projectile penetrating concrete target[31]

1.2 計算模型

基于上述討論，剛性彈侵徹過程中所受阻力如圖3 所示，其中Fm為隧道區恒定阻力。

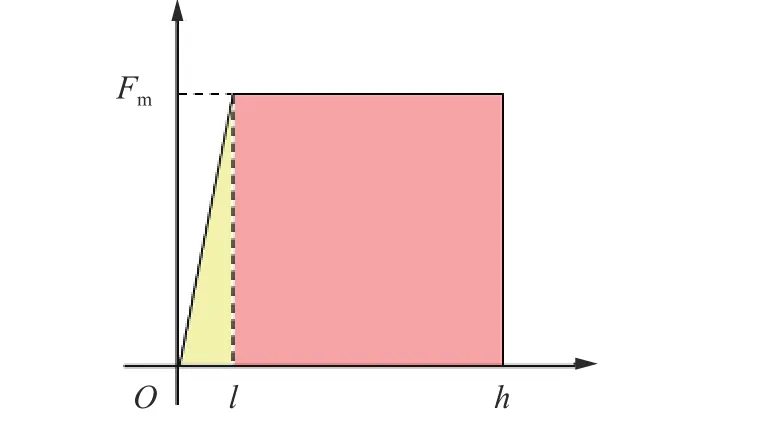
圖3 線性上升-恒定的侵徹阻力模型Fig.3 A linear increasing-constant penetration resistance model

依據能量守恒定律，彈體動能全部轉化為阻力做功，即：

需要指出的是，由于A是Forrestal 等[29,32]基于試驗數據反向擬合得到，式（5）仍是一種半經驗公式。注意到確定A值大多是基于縮比試驗數據，彈體口徑較小，使得式（5）的適用范圍有限，若要將其推廣應用到大口徑鉆地彈則必須考慮尺寸效應的影響。

1.3 尺寸效應系數

尺寸效應可簡單地表述為幾何相似的彈體侵徹同一混凝土靶體時，無量綱侵徹深度不相等。吳飚等[33]開展了7 種不同比尺的彈體以450 m/s 的速度分別侵徹C40 和C60 混凝土靶體的試驗研究，結果表明，無量綱侵徹深度h/d隨彈徑的增加而增加。Wu 等[34]認為造成尺寸效應的主要原因是混凝土中粗骨料的粒徑，即按照彈體比例縮放靶體模型時，粗骨料的粒徑沒有進行相應縮比。而后彭永等[35]基于混凝土靶體的細觀有限元模型，開展了相應數值模擬研究，驗證了上述結論。Canfield 等[36]開展的侵徹試驗中對粗骨料粒徑進行了相應地縮比（也即保證彈徑與粗骨料粒徑比不變），結果表明無量綱侵徹深度滿足相似律，進一步驗證了上述結論。但是，從量綱分析可知，影響尺寸效應還有材料的應變率和斷裂能等[37-38]。總之，目前尚未完全揭示彈體侵徹的尺寸效應的作用機制。為此，本文中采用已有大口徑試驗數據修正的方法考慮尺寸效應。即在式（5）的基礎上引入彈徑修正系數λd：

為確定彈徑修正系數λd的取值，收集了145 組剛性卵彈侵徹混凝土靶體的試驗數據[1,8,19,28-29,32-34,39-48]，彈徑范圍為10～400 mm，彈體初速度范圍為100～700 m/s，通過以下方法對彈徑修正系數λd進行確定。

首先，采用未修正的式（5）對收集到的試驗數據進行計算，并求得式（5）與試驗值的誤差；然后，根據彈體直徑分階段分析誤差數據，求得每種分類下的平均誤差，如圖4 中紅點所示。可以看出，平均誤差可分為3 個階段：當彈徑在10～50 mm 時，式（5）計算值大于試驗值，且平均誤差約在10%；當彈徑在50～130 mm 時，式（5）計算值小于試驗值，且隨著彈徑增加，平均誤差逐漸增大；而當彈徑大于130 mm時，式（5）計算值小于試驗值，且誤差穩定在約35%。

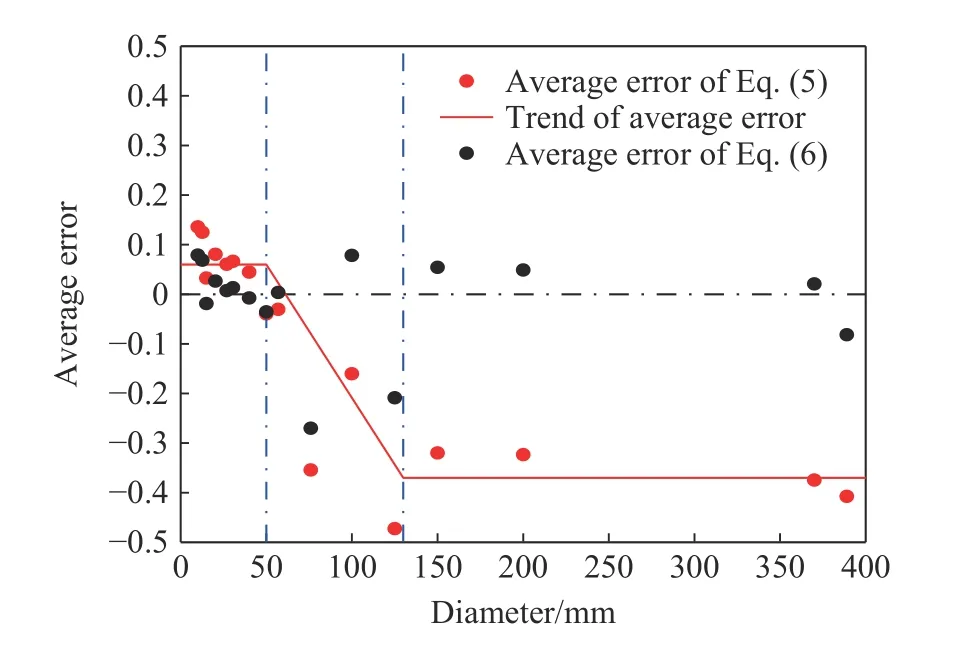
圖4 預測侵徹深度的平均誤差Fig.4 Average error of predicted penetration depth

根據上述規律，可得出彈徑修正系數λd的取值如表1 所示，分為3 個階段：當彈徑小于40 mm 時，λd取0.95；當彈徑在40～130 mm 之間時，λd在0.95～1.55 之間線性插值；當彈徑大于130 mm 時，λd取1.55。經過彈徑修正系數的修正之后，對平均誤差重新進行計算，如圖4 中黑點所示，發現式（6）預測不同彈徑的侵徹深度的平均誤差大多約在±10%。

表1 彈徑修正系數取值表Table 1 Correction factor for projectile diameter

圖5 給出了考慮彈徑修正系數的式（6）預測的侵徹深度和試驗數據的對比（試驗數據按照l/d的取值分為3 類）。圖中紅色實線為式（5）中無量綱侵徹深度h/d與無量綱因子I之間關系，淡紅色點為原始試驗數據，而黑色點則為經過彈徑修正系數倒數1/λd逆修正后的試驗數據。通過比較可以發現，式（6）預測值與試驗數據吻合較好，經過彈徑修正系數的修正，原來較為彌散的試驗數據進一步靠近紅色實線，說明提出的彈徑修正系數有效提高了侵徹深度的預測精度。

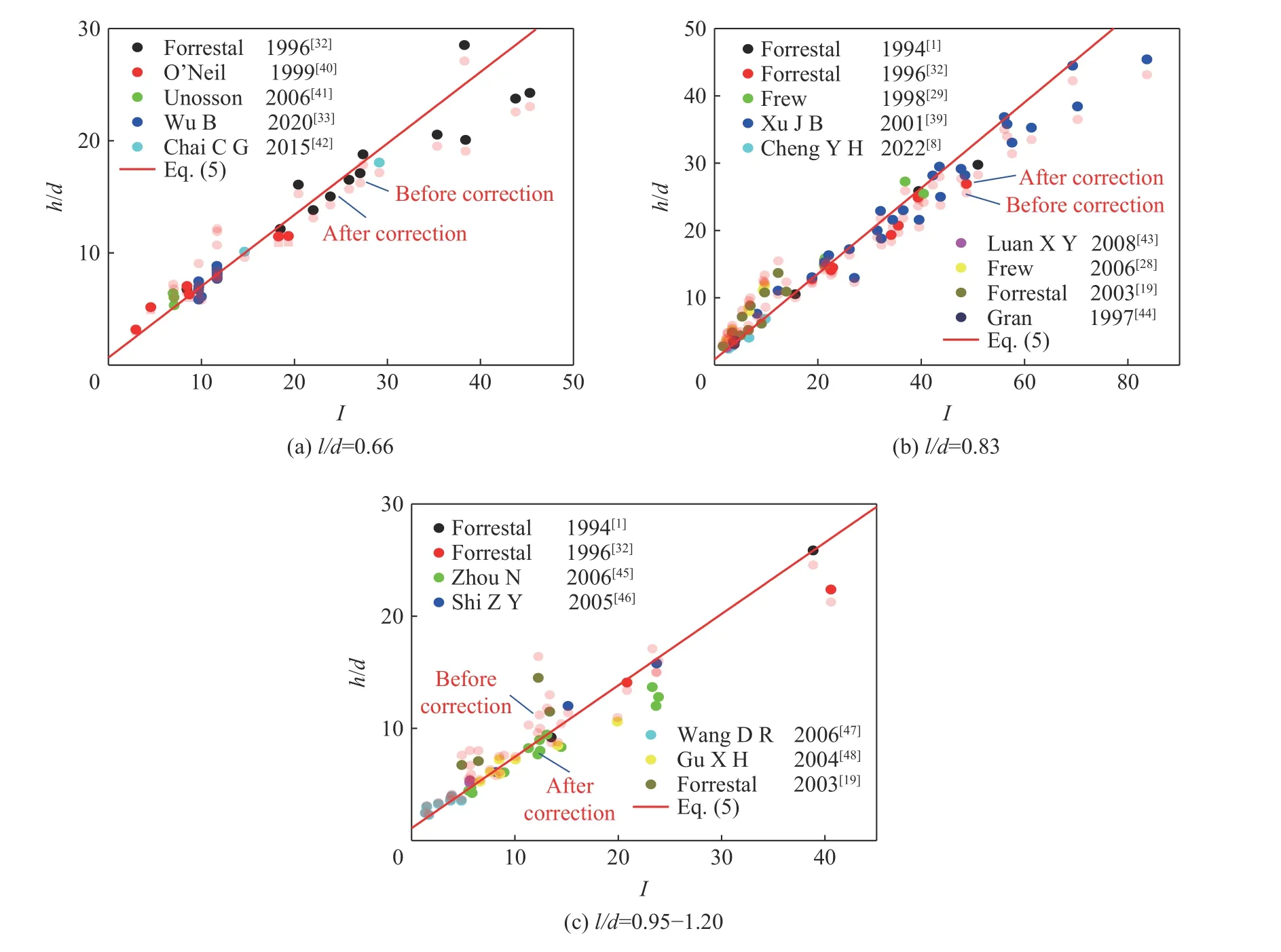
圖5 式（5）預測值和試驗值的對比Fig.5 Comparison of penetration depth predicted by Eq.(5) with test data

1.4 與已有經驗公式的對比分析

選取目前廣泛使用的ACE 公式[11]和NDRC 公式[12]進行對比分析，ACE 公式為：

式中：N*為彈頭形狀系數，對于平頭、半球、鈍頭和尖頭彈體分別取0.72、0.84、1.00 和1.14。

主要關注大口徑彈體的中低速剛性侵徹，因此選取了周寧等[45]、程月華等[8]、吳飚等[33]和王德榮等[47]開展的彈徑100 mm 及以上的15 組大口徑彈體侵徹混凝土靶體的試驗數據與本文中提出公式、ACE 公式和NDRC 公式進行對比分析，試驗工況及各公式預測誤差如表2 所示。可以看出，本文中提出公式計算得到的預測值與試驗值的平均誤差為5.5%，具有較高的預測精度。而ACE 公式和NDRC 公式的預測值與試驗值相比有較大的差異，ACE 公式平均誤差約為15.7%，NDRC 公式的平均誤差約為24.9%，且兩者計算得出的侵徹深度均小于試驗侵徹深度，對防護工程設計來說是偏于危險的。

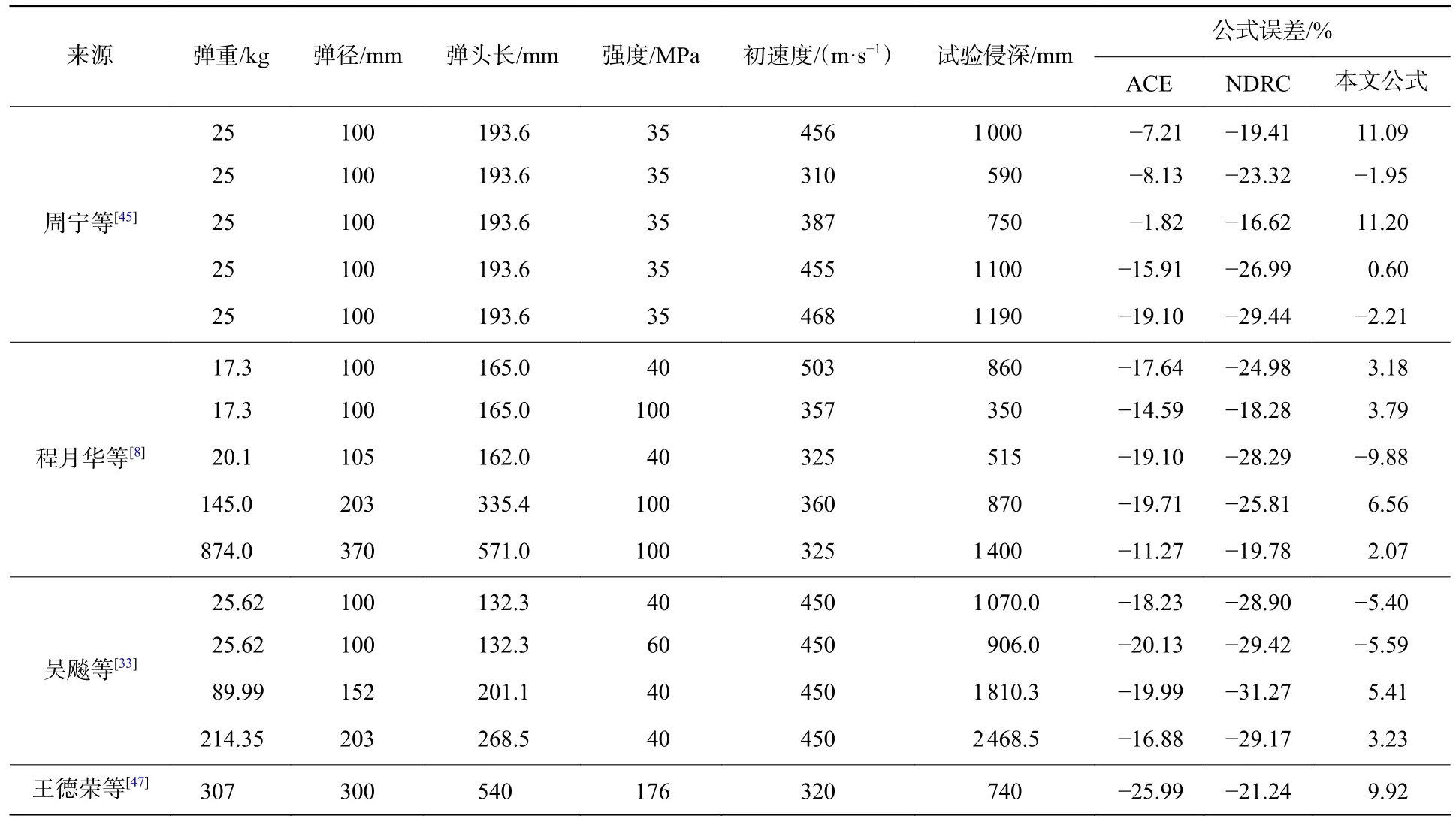
表2 大口徑彈體侵徹混凝土靶體試驗數據及各公式預測誤差Table 2 Test data and formulas error for projectile penetrating into concrete targets with large projectile diameters

2 剛性彈貫穿混凝土厚靶的計算模型

首先對剛性彈貫穿混凝土厚靶的3 個階段進行細致分析，提出靶背震塌坑破壞形成的條件，進一步建立后坑高度的計算模型；在此基礎上給出臨界貫穿厚度、彈道極限以及殘余速度的計算模型，并通過試驗數據的驗證；最后分析4 種典型鉆地彈的侵徹不貫穿系數。

2.1 震塌坑形成條件

基于大量的貫穿試驗[12,31,49-52]，對于防護工程主要關注的厚靶而言，貫穿過程可分為前開坑、隧道區和后震塌坑（簡稱后坑）3 個典型階段，如圖6 所示。

圖6 彈體貫穿混凝土厚靶的3 個階段試驗照片Fig.6 Post-test pictures of three stages for projectile penetrating into thick concrete target

前開坑通常認為是由彈體沖擊下靶體材料發生剪切及拉伸（上自由表面反射的拉伸波引起）破壞造成的，隧道區主要由混凝土材料發生內部孔隙壓實破壞所致[53-54]。而對于后坑的形成，目前仍有爭議，主要有下述兩種觀點。Li 等[12]認為后坑機理為彈體侵徹下的剪切沖塞效應，即震塌塊與靶體界面的剪應力達到材料剪切強度破壞；而武海軍等[55]、鄧國強等[56]則認為后坑破壞為壓縮波在靶體后自由表面反射產生拉伸波引起的層裂拉伸破壞。Zhang 等[53]和Wang 等[54]基于綜合考慮剪切損傷、拉伸損傷和體積壓縮損傷的Kong-Fang 模型[57]對彈體貫穿混凝土靶體機理進行了精細化數值模擬分析，發現后坑主要由拉伸破壞引起，如圖7（b）所示。

圖7 數值模擬得到的彈體貫穿混凝土靶體的損傷云圖[53]Fig.7 Damage contour in concrete subjected to projectile penetration obtained from numerical simulation[53]

2.2 臨界貫穿厚度

根據圖7 的數值模擬結果可判斷后坑的形成機制主要為拉伸破壞，基于Chen 等[14-15]貫穿公式的推導過程可建立臨界貫穿厚度的相關計算模型，如圖8 所示，其中xf和xr分別為開坑和后坑高度，ft為混凝土拉伸強度，α 為錐形后坑的半錐角，As為后坑的表面積，hbal為臨界貫穿厚度。

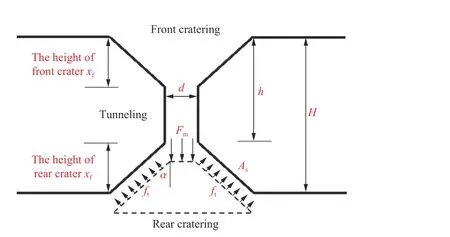
圖8 彈體臨界貫穿模型示意圖Fig.8 Schematic diagram of critical penetration

臨界貫穿厚度是指彈體侵徹不貫穿時靶體的最小厚度，此時后坑塊體形成但速度為零，由力的平衡條件可得：

錐形后坑的表面積As可表示為：

聯立式（9）～（10）可得

則臨界貫穿厚度的無量綱形式可寫為：

式中：侵徹深度h由式（6）計算得到。

從式（11）中可以看出，無量綱后坑高度主要與混凝土壓拉強度比、阻力系數A和錐形后坑半錐角α 等3 個參數相關，其中最關鍵的參數為α。已有剛性卵彈貫穿混凝土靶體試驗中，僅有少數關注了錐形后坑的半錐角。其中Dancygier 等[49]測量了普通混凝土和高強混凝土后坑半錐角的平均值分別為66.1°、76.3°，Li 等[31]試驗測得C35 混凝土靶體的后坑半錐角平均值為67.6°，Wu 等[51]試驗測得C40 混凝土靶體后坑半錐角平均值為64.6°。可以看出，對于普通混凝土，后坑半錐角的測量值均在約65°，而高強混凝土的后坑半錐角的試驗數據有限，后文為便于分析，后坑半錐角統一取65°。

為驗證后坑高度式（11）的可靠性，選取Hanchak 等[50]、Li 等[31]和Wu 等[51]的實測數據進行對比分析，對比結果如表3 所示。可以看出，公式預測結果與試驗結果較為接近，且大部分無量綱后坑高度均在2d～3d（d為彈體直徑）之間，這與Peng 等[16]基于大量試驗數據擬合得到的后坑高度2.5d一致。

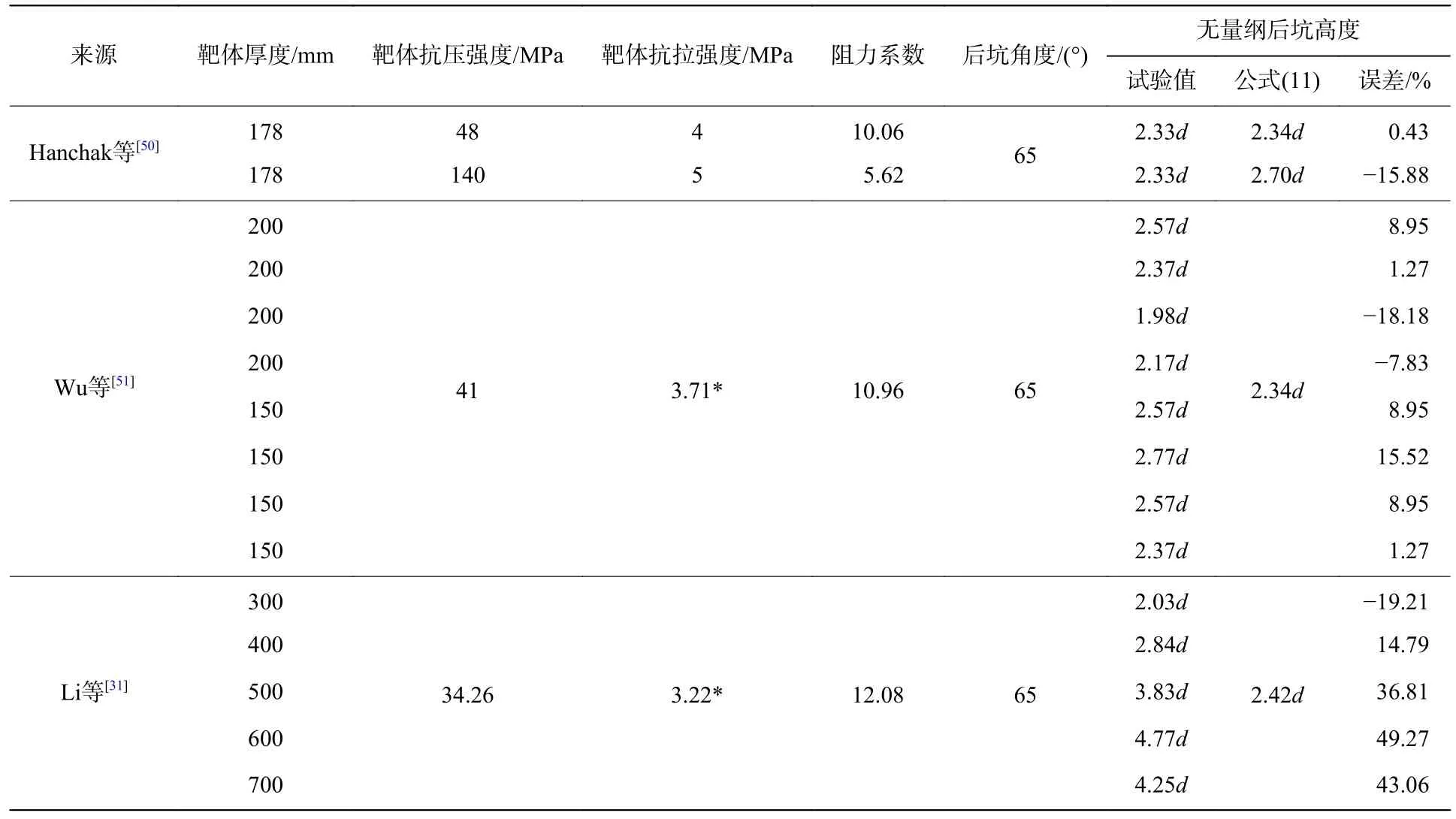
表3 后坑高度預測值和試驗值的對比Table 3 Comparison of scabbing depth predicted by Eq.(11) with test data

2.3 彈道極限和殘余速度

彈道極限vbal即在給定靶體厚度H的情況下，彈體不貫穿靶體的最大速度，可通過聯立式（6）、（11）～（12）求得為：

式中：mc為錐形后坑塊的質量，可表示為：

式中：ρc為混凝土密度。聯立式（14）～（15）可求得彈體殘余速度為：

為驗證式（13）和（17）的可靠性，選取Hanchak 等[50]、Wu 等[51]和薛建鋒等[52]進行的彈體貫穿混凝土靶體試驗進行驗證，注意到Hanchak 等[50]開展的試驗既有貫穿又有未貫穿，可同時驗證式（13）和（17）。公式預測與試驗對比如圖9 所示，可以看出式（17）預測的殘余速度與試驗吻合較好，且式（13）預測的彈道極限與Hanchak 等[50]試驗數據相吻合（圖9 中粉紅色標注處）。

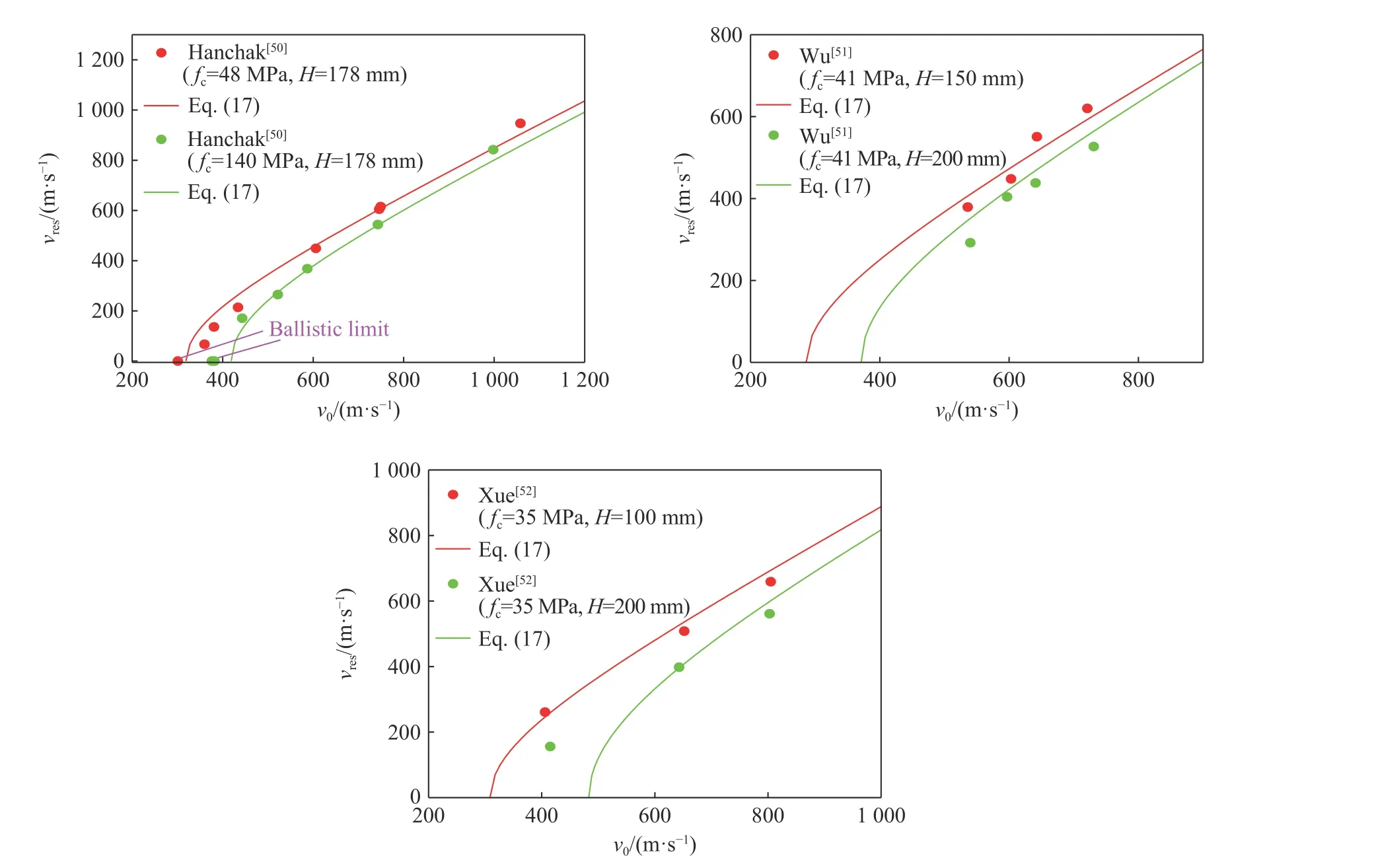
圖9 殘余速度和彈道極限的預測結果和試驗數據的對比Fig.9 Comparison of residual velocity and ballistic limit between predictions and test data

2.4 典型鉆地彈的侵徹不貫穿系數

侵徹不貫穿系數可為防護結構的遮彈層設計提供直接參考，侵徹不貫穿系數Kg為在臨界貫穿狀態下，臨界貫穿厚度與彈體侵徹深度的比值，即：

結合式（12）可得：

因此，根據本文中提出的侵徹深度計算式（6）和后坑高度計算式（11）即可快速得到侵徹不貫穿系數。通過對式（19）簡單分析可知，Kg的大小主要取決于后坑高度與侵徹深度的比值，比值越大，侵徹不貫穿系數也就越大，反之則越小。根據2.2 節分析，后坑高度的大小雖與靶體強度相關，但不同強度靶體的后坑高度差異不大，均在2d～3d之間。因此，侵徹不貫穿系數Kg的大小主要取決于彈體侵徹能力的強弱，即彈體侵徹能力越弱，Kg越大，反之則越小。

圖10 給出了BLU-109/B、BLU-122/B、WDU-43/B 和SDB 等4 種典型戰斗部以200～500 m/s 初速度侵徹C40、C80、CF120（強度為120 MPa 的纖維增強超高性能混凝土）的侵徹不貫穿系數，其中4 種戰斗部的公開資料參見文獻[59-60]。由圖10 可以看出幾點規律：隨著彈體侵徹速度的增加，后坑高度與侵徹深度的比值減小，侵徹不貫穿系數逐漸減小并趨近于1；隨著靶體強度的增加，侵徹深度減小，后坑高度與侵徹深度的比值變大，侵徹不貫穿系數小幅增加，但變化不明顯；4 種戰斗部當中，BLU-109/B 的侵徹不貫穿系數最大，其余3 種戰斗部相差不大，主要由于BLU-109/B 的侵徹能力較弱。當以300 m/s 的速度侵徹C80 混凝土時，4 種戰斗部的無量綱侵徹深度分別為3.75、6.80、7.52 和6.86，侵徹不貫穿系數分別為1.63、1.35、1.31 和1.34。

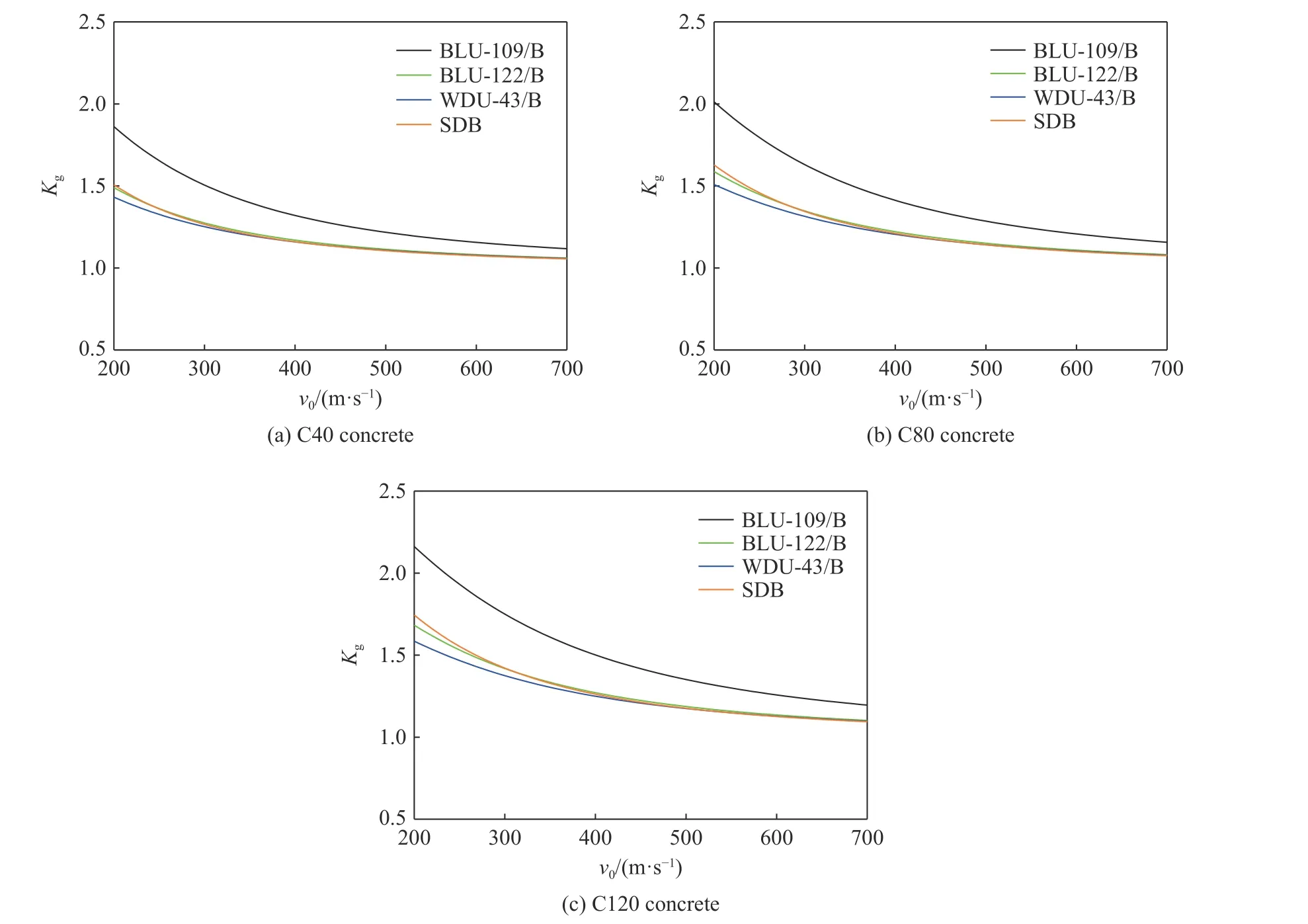
圖10 四種典型戰斗部的侵徹不貫穿系數Fig.10 Coefficients of concrete targets in preventing perforation for four typical warheads

3 結 論

為解決現有彈體對混凝土靶體侵徹深度計算公式預測精度不高、形式復雜，以及臨界貫穿厚度缺乏理論基礎等問題，基于已有大量的試驗數據，對彈徑為10～100 mm、彈速為100～700 m/s 情況下剛性卵彈垂直正侵徹/貫穿混凝土靶體的實用化計算模型進行了研究，主要結論如下。

（1）通過對剛性彈侵徹混凝土靶體的阻力分析，提出線性上升-恒定的兩階段阻力模型，并基于此建立侵徹深度的計算公式，然后根據大量的試驗數據，引入考慮尺寸效應影響的彈徑修正系數，大幅提高了計算公式的預測精度。

（2）基于15 組彈徑在100 mm（包含）以上的侵徹試驗，對本文中提出公式及已有常用公式進行了對比分析，發現本文中公式預測結果的平均誤差約為5.4%，而ACE 和NDRC 公式的平均誤差約為15.7%和24.9%，驗證了本文中公式預測大口徑、大長徑比的彈體侵徹深度的可靠性和優越性。

（3）基于后坑由拉伸破壞引起的基本假定，得到了后坑高度的計算公式，并給出了臨界貫穿厚度、彈道極限和殘余速度的計算模型，通過與現有的試驗數據對比分析，驗證了上述模型的可靠性。

（4）對4 種典型鉆地彈戰斗部的侵徹不貫穿系數討論分析發現，侵徹不貫穿系數隨著侵徹速度的增加會逐漸減小但始終大于1，隨著靶體的強度的增加會有較小幅的增大。