六自由度上肢康復機器人運動學分析及軌跡規劃

馬曉君，劉訓報，賈秋生，劉德勝，袁銘潤，劉玉陽

（1.佳木斯大學 a.機械工程學院；b.信息電子技術學院，黑龍江 佳木斯 154007；2.哈爾濱軸承集團有限公司，哈爾濱 150002）

0 引言

李宇淇等[1]為了探究上肢康復機器人聯合康復訓練對腦卒中恢復期患者上肢運動功能的影響，在南方醫科大學珠江醫院對40例腦卒中恢復期患者進行了實驗研究，結果表明，上肢康復機器人聯合上肢康復訓練可以有效改善腦卒中恢復期患者上肢運動功能，促進偏癱上肢肌肉激活和運動單位募集同步化，提高日常生活能力，值得臨床推廣應用。

Qian等[2]提出一種基于神經網絡的平面上肢康復機器人，其采用導納控制策略實現主動訓練模式，結果表明，患者與健康受試者在交互作用力、運動偏差、運動范圍和運動平滑度方面存在顯著差異，圓形軌跡跟蹤的運動范圍和運動平滑度與臨床頻率測定裝置呈正相關。Roy等[3]針對現有上肢康復原型的旋轉關節設計了一個2自由度PID控制器，仿真和實驗數據表明，所提出的2DOF PID控制器類似于一種適合單自由度肘部運動的控制器。Yan等[4]對人體上肢的解剖結構的了解，設計了一種廣義肩關節上肢康復機器人，通過建立上肢康復機器人運動學模型，并進行運動學分析，求出了逆運動學解條件數的標定、可操作性橢球分析及二者的比較配置方案的結果，來對比在正常上肢姿勢下人體的運動學性能。

Zhao等[5]提出了新的機器人結構，將柔性繩索與外骨骼結合使用，以確保其與患者上肢相連的運動部件可以達到輕便、準確、靈活的觸覺效果。Wang等[6]為了提高上肢外骨骼機器人在康復過程中的人機交互性能訓練，對卡爾曼濾波與削波濾波二者相合提出了一種改進方法，并使其達到自適應效果，以減輕采集信號的噪聲和延時。所設計的系統有效地遵循了預期的運動意圖，證明該方法是對上肢人機交互控制的一個重大改進。Fang等[7]為了分析新型外骨骼的電動機轉矩和關節轉矩之間的關系，提出了一種將電動機運動映射到關節運動的轉換算法。為了驗證所提算法是否有效，對其進行了軌跡跟蹤仿真，結果證明了所提算法的有效性。Li等[8]采用逆坐標系法求解外骨骼串聯等效構型的逆運動學，結果表明所提出的逆運動學算法和軌跡規劃方法是有效的。

針對腦卒中患者上肢康復訓練問題，本文對設計的六自由度上肢康復機器人進行了運動學仿真及五次多項式軌跡規劃，并最終驗證了其設計的合理性。

1 上肢結構及運動范圍分析

上肢手臂主要由肱骨、橈骨、尺骨、腕骨、掌骨、指骨組成，可以實現上肢的空間運動。

圖1 人體上肢骨骼結構圖

肩關節是人體比較靈活的一個關節，具有3個自由度，其活動的范圍非常大，肩關節活動度的正常范圍，主要包括：外展一般情況下為90°，內收為20°～45°，前屈為70°～90°，后伸為30°～40°，內旋為45°～75°，外旋為45°～60°。肩關節的3種運動形式如圖2所示。

圖2 肩關節的3種運動形式

肘關節位于上肢的中部，肘關節和小臂連接在一起具有2個自由度，由上臂肱骨的髁部和前臂尺骨的近端，以及前臂橈骨的橈骨頭共同構成，是一種復關節。肘關節屈曲的范圍因人而異，一般可以達到135°～150°，肘關節向后伸的角度相對小一些，一般在10°以內。肘關節和小臂主要運動形式如圖3所示。

圖3 肘關節和腕關節主要運動形式

圖4 上肢康復機器人模型

腕關節主要有2個自由度，腕關節主要是屈曲、伸展和內收、外展運動。

2 康復機器人結構設計

2.1 外骨骼上肢康復機器人模型

通過對人體上肢結構的分析，設計了一款6個自由度的上肢康復機器人，傳動件選擇伺服電動機，具有質量輕、穿戴方便的優點。上肢康復機器人可以完成肩關節的3個自由度運動，肘關節和小臂的2個自由度運動，腕關節的屈曲、伸展的1個自由度運動，具有康復訓練的功能。

上肢康復機器人裝置主要由10個部分組成，即康復機器人旋轉手柄、轉動部件、角接觸球軸承S7210、小臂連桿、伺服電動機、大臂連桿、肩部連桿、肩部滑桿、肩部滑軌、背板。上肢康復機器人裝置可以實現手臂的空間范圍的運動，主要由伺服電動機驅動手臂的運動，旋轉手柄可以實現手腕在空間范圍的運動，肩寬采用可調節式滿足不同患者康復使用。康復訓練模式采用被動訓練和主動訓練這兩種模式，被動訓練模式是通過伺服電動機帶動的被動康復訓練，主動訓練模式適用于患者主動進行康復訓練。

依據中國成年人人體上肢尺寸數據GB/T 10000-88，滿足90%中國成年人患者的穿戴需求，上肢康復機器人尺寸設計如表1所示。

表1 上肢康復機器人設計參數

2.2 步進電動機選型及估算

2.2.1 肘關節電動機選型及估算

小臂質量定為0.6 kg，肘關節驅動電動機主要克服小臂做功，考慮到摩擦及傳動效率影響，小臂運動到水平位置時，電動機轉矩最大，此時轉矩為T1=mgD1=0.6×9.8×0.253=1.48764 N·m。因此電動機選擇額定轉矩為2 N·m的伺服電動機。

2.2.2 肩關節電動機選型估算

大臂質量定為0.7 kg，肩關節電動機主要克服大臂和小臂做功，電動機達到極限位置時的轉矩最大，最大轉矩為T2=(m1+m2)gD2=(0.6+0.7)×9.8×(0.333+0.188+0.065)=7.46564 N·m。因此電動機選擇額定轉矩為8 N·m的伺服電動機。

3 上肢康復機器人運動學

從機械的角度看，上肢康復機器人可以用一系列轉動關節或移動關節連接的剛體表示。可以通過每一連桿相對于前一連桿的基本運動合成得到上肢康復機器人的運動結果。因此，為了表示空間中的康復訓練路徑，有必要描述出末端執行器的位置和方向。若要讓上肢康復機器人安全、準確地完成規定的康復訓練，應該對其進行運動學分析。建立上肢康復機器人D-H坐標系，對末端位置進行求解，如圖5所示。圖5中：L1=333 mm，L2=188 mm，L3=65 mm。上肢康復機器人運動參數如表2所示。

表2 上肢康復機器人運動參數

圖5 上肢康復機器人D-H坐標系

由機器人運動學知識可以得到連桿坐標系間的齊次變換矩陣為

式中，正弦和余弦可以簡化為：sin θi=si，cos θi=ci。

由矩陣變換的知識，可以得到上肢康復機器人的Ai變換為：

T6為上肢康復機器人基坐標系和末端坐標系之間的總變換：

計算可得：

4 Adams運動學仿真

肩關節和肘關節的屈伸是康復運動過程中最常做的運動，為了使上肢康復機器人更加真實地模擬人體康復運動的過程，在Adams中對肩關節和肘關節屈伸康復訓練進行了運動學仿真。

肩關節外展內收是上肢康復運動的主要形式，肩關節外展設為90°，內收為20°。肘關節運動主要是伸屈運動，伸展設為180°，彎屈為135°。腕關節主要運動是外擺內收，外擺為60°，內收為60°。肩關節、肘關節、腕關節康復運動都是多次往復運動，在Adams中編寫驅動函數，讓上肢康復機器人規定路線運動。仿真時間設置為20 s，步長為1000，具體驅動函數如下：

如圖6所示，利用腕關節的外擺內收的仿真數據，最終得到了線速度和角速度的曲線圖。經分析可知，線速度和角速度都是平穩變化，沒有發生突變，可以達到穩定的康復運動效果。

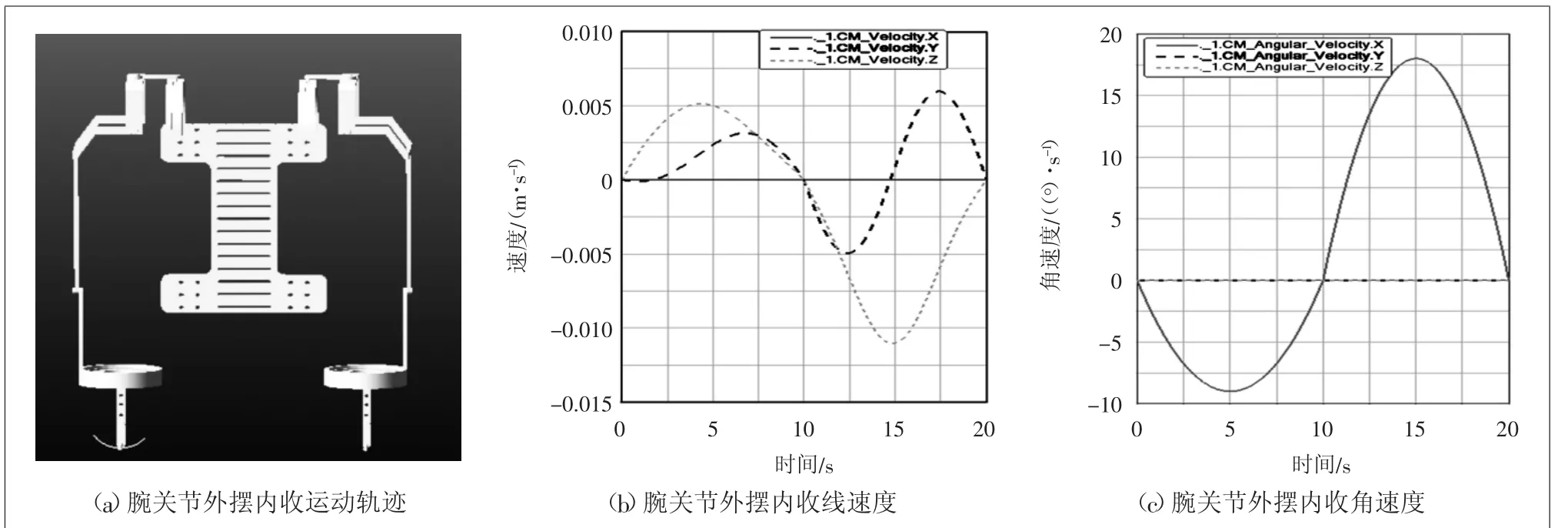
圖6 腕關節外擺內收

如圖7所示，肘關節線速度和角速度運動曲線表明，在屈伸的過程中，速度呈現出簡諧運動，速度增加或減小的過程中沒有發生較大的波動，能夠完成肘關節的屈伸康復運動。

圖7 肘關節屈伸

如圖8所示，肩關節的運動外展內收表明，肩關節可以在一定的速度下進行康復運動，運動過程中速度沒有發生突變，可以完成肩關節的外展內收動作。

圖8 肩關節外展內收

5 基于Matlab的機器人軌跡規劃

5.1 六自由度上肢康復機器人模型建立

利用在Matlab中應用機器人工具箱中的link函數和serillink函數建立上肢康復機器人運動模型。使用表2的參數，建立名為“上肢康復機器人”的模型，程序如下：

5.2 空間軌跡規劃

空間軌跡規劃主要包括關節空間軌跡規劃和笛卡兒空間軌跡規劃。六自由度上肢康復機器人關節空間軌跡規劃和笛卡兒空間軌跡規劃如圖9所示。

圖9 上肢康復機器人空間軌跡規劃曲線

關節空間軌跡規劃采用五次多項式規劃，五次多項式有6個待定系數，可同時對起始點和目標點的角度、角速度和角加速度給出約束條件，設關節角計算公式為：

將相鄰的兩個插值點看作一小段軌跡的起點和終點，分別用q0和qf表示，約束起始速度為v0，終止速度為vf，計算公式為：

在Matlab中采用五次多項式進行上肢康復機器人關節空間軌跡規劃，first_theta=[0 0 0 -pi/2 0 pi/2]初始關節角為上肢康復機器人處于水平伸展位置，final_theta=[pi/2 pi/2 pi/10 -1.25*pi pi 3*pi/4] 最終關節角為肩關節內收、肘關節屈伸、腕關節內收一定角度，采樣點數為200個，對規劃軌跡進行仿真。五次多項式插值法所得到的軌跡加速度也是平滑曲線，并沒有出現突變的情況。在機器人系統中，關節角加速度沒有出現突變現象意味著關節電動機不會受到沖擊，關節角加速度曲線平滑連續可以保證電動機平穩運行。首末兩點的速度和加速度都可以約束為零，由此可知六自由度上肢康復機器人可以平穩地進行康復訓練，不會出現安全問題。

6 結論

1）本文對人體上肢的生理結構進行分析，根據其上肢關節的自由度范圍設計了一款可穿戴式六自由度上肢外骨骼康復機器人，并對其進行了實體建模，估算出電動機型號。建立了上肢康復機器人D-H坐標系，求出末端軌跡坐標，在Adams中設置step函數，對上肢康復運動進行了仿真，獲得了線速度、角速度運動參數，最終確定康復機器人可以完成肩部、肘部、手腕的運動，驗證了機器人設計的實用性。

2）通過Matlab中六自由度上肢康復機器人的軌跡規劃仿真，位置、速度、加速度曲線平滑連續，可平穩地完成康復訓練過程，保證患者康復訓練安全性，證明了穿戴式六自由度上肢康復機器人設計的合理性，為上肢康復機器人研究提供了理論基礎。