基于阻抗模型的工業(yè)機(jī)器人磨拋柔順控制

王曉永，解海亮

（1.內(nèi)蒙古第一機(jī)械集團(tuán)股份有限公司，內(nèi)蒙古 包頭 014030；2.華中科技大學(xué) 國(guó)家數(shù)控系統(tǒng)工程技術(shù)研究中心，武漢 430074）

0 引言

為了避免智能化加工設(shè)備加工過(guò)程中工具與工件之間的接觸狀態(tài)切換引起振動(dòng)與沖擊，國(guó)內(nèi)外研究機(jī)構(gòu)提出柔順控制策略[1-2]。1985年，N.Hogan[3]提出在系統(tǒng)操作過(guò)程中，僅僅考慮運(yùn)動(dòng)學(xué)量的相互匹配是不夠充分的，同時(shí)應(yīng)該考慮2個(gè)物體的阻抗特性。由此提出了阻抗控制，實(shí)現(xiàn)了操作過(guò)程中的運(yùn)動(dòng)學(xué)約束、動(dòng)力學(xué)交互、抓取和避障的統(tǒng)一方法，建立起力與位置、速度、加速度之間的關(guān)系。A.Lopes等[4]采用基于位置的阻抗控制策略，設(shè)計(jì)了一款末端恒力控制裝置，通過(guò)調(diào)整阻抗模型中剛度參數(shù)、阻尼參數(shù)及慣性參數(shù)，使得末端執(zhí)行器在受到作用力時(shí)表現(xiàn)出不同的動(dòng)態(tài)響應(yīng)，以達(dá)到順應(yīng)未知加工狀況的目的。2018年，Duan J.J.[5]提出基于追蹤誤差采用自適應(yīng)的方式實(shí)時(shí)修改阻抗模型參數(shù)，以達(dá)到對(duì)期望力的動(dòng)態(tài)追蹤。2019年，Zhou P.等[6]針對(duì)航空發(fā)動(dòng)機(jī)復(fù)雜葉片提出采用模糊控制算法結(jié)合經(jīng)典PID理論，以實(shí)現(xiàn)自適應(yīng)恒力打磨，改善銑削后的葉片表面質(zhì)量。周亞軍[7]將ATI公司的六維力傳感器集成到機(jī)器人控制系統(tǒng)，為機(jī)器人磨拋系統(tǒng)增加力感知功能，實(shí)時(shí)監(jiān)測(cè)磨拋過(guò)程中的磨拋力，采用基于位置的阻抗控制策略對(duì)末端執(zhí)行器的位置進(jìn)行補(bǔ)償，改變工件與工具之間的接觸變形量，達(dá)到恒力加工的目的。張琛[8]利用六維力傳感器獲取機(jī)器人末端執(zhí)行器與打磨工件之間不同接觸狀態(tài)下的實(shí)際接觸力，進(jìn)而建立起與末端執(zhí)行器相接觸的環(huán)境剛度模型。基于環(huán)境剛度模型，結(jié)合力覺(jué)感知系統(tǒng)修正末端執(zhí)行器的位置，達(dá)到恒力打磨的目標(biāo)。2019年，在采用基于位置的阻抗控制時(shí)，針對(duì)環(huán)境剛度模型未知的情況，Liang X.Q.等[9]提出通過(guò)在線估算環(huán)境位置及環(huán)境剛度來(lái)設(shè)計(jì)機(jī)器人運(yùn)動(dòng)軌跡，然而機(jī)器人始終存在位置跟蹤誤差，為了減少力追蹤誤差，采用迭代學(xué)習(xí)控制算法來(lái)減少位置追蹤誤差。Sun T.等[10]針對(duì)獲取準(zhǔn)確機(jī)器人動(dòng)力學(xué)模型難度較大這一問(wèn)題，提出了一種變阻抗控制方法，所提出的阻抗控制器可以采用PID形式實(shí)現(xiàn)，具有結(jié)構(gòu)簡(jiǎn)單、易于實(shí)現(xiàn)和保證控制穩(wěn)定性的優(yōu)點(diǎn)。基于Tikhonovs定理，證明了閉環(huán)控制系統(tǒng)具有半全局實(shí)際指數(shù)穩(wěn)定性。以五桿并聯(lián)機(jī)器人為例，說(shuō)明了所提變阻抗控制器的有效性。Zhang X.[11]采用變阻抗控制策略，通過(guò)改變期望剛度和期望阻尼來(lái)提高機(jī)器人與環(huán)境交互的順應(yīng)性和魯棒性。針對(duì)機(jī)器人與環(huán)境交互問(wèn)題，提出了一種基于神經(jīng)網(wǎng)絡(luò)的變阻抗控制器，通過(guò)變阻抗控制誤差的收斂增強(qiáng)系統(tǒng)的魯棒性。Xiong G.[12]提出了一種7自由度冗余度機(jī)械臂阻抗控制方法。在關(guān)節(jié)中間描述了冗余度機(jī)械臂的阻抗運(yùn)動(dòng)，建立了關(guān)節(jié)空間下的阻抗方程。為成功獲取關(guān)節(jié)角速度，設(shè)計(jì)了高增益觀測(cè)器，驗(yàn)證了所提控制方法的穩(wěn)定性。

然而，上述應(yīng)用于航空發(fā)動(dòng)機(jī)葉片存在力跟蹤效果差、抗沖擊特性差或響應(yīng)速度慢等問(wèn)題，都無(wú)法很好地解決加工具有自由曲面、變厚、非對(duì)稱特點(diǎn)的復(fù)雜構(gòu)件的問(wèn)題。此外，現(xiàn)有的末端磨拋執(zhí)行器控制策略[13]難以實(shí)現(xiàn)工藝參數(shù)的自律調(diào)整，基于材料去除模型的主動(dòng)柔順控制策略研究又十分匱乏。因此研究基于模型驅(qū)動(dòng)的智能柔順控制策略，對(duì)實(shí)現(xiàn)磨拋執(zhí)行器的磨拋工藝自律調(diào)整具有重要意義。

1 磨拋執(zhí)行器動(dòng)力學(xué)建模

力位混合控制[14]和阻抗控制都是在被控對(duì)象運(yùn)動(dòng)中實(shí)現(xiàn)對(duì)外界接觸力柔順響應(yīng)。因此需要首先考慮機(jī)器人柔順磨拋執(zhí)行器的動(dòng)力學(xué)模型，即在受到外界作用力下，磨拋執(zhí)行器的伺服電動(dòng)機(jī)輸出力矩與磨拋執(zhí)行器運(yùn)動(dòng)過(guò)程中運(yùn)動(dòng)量參數(shù)之間的定量關(guān)系。常用的動(dòng)力學(xué)建模的方法有牛頓-歐拉迭代法及拉格朗日法。其中牛頓-歐拉公式被認(rèn)為主要是用來(lái)解決在動(dòng)力學(xué)建模中遇到的力平衡問(wèn)題，而拉格朗日動(dòng)力學(xué)方程則是一種從系統(tǒng)能量的角度進(jìn)行動(dòng)力學(xué)建模的一種方法。本文將基于拉格朗日法建立機(jī)器人柔順磨拋執(zhí)行器的動(dòng)力學(xué)方程。

磨拋執(zhí)行器結(jié)構(gòu)如圖1所示。由于磨拋執(zhí)行器的浮動(dòng)方向與重力方向互相垂直，因此磨拋執(zhí)行器的勢(shì)能函數(shù)為一常量函數(shù)。磨拋執(zhí)行器運(yùn)動(dòng)的動(dòng)力來(lái)源于伺服電動(dòng)機(jī)，因此基于能量守恒原理且考慮摩擦力f與外力Fext，將伺服電動(dòng)機(jī)的驅(qū)動(dòng)力矩τ與激勵(lì)力矢量F之間進(jìn)行轉(zhuǎn)換：

圖1 浮動(dòng)磨拋執(zhí)行器三維模型

式中：x為磨拋執(zhí)行器浮動(dòng)方向上的位置；Fext為外力；Ff為摩擦力；η為能量從伺服電動(dòng)機(jī)傳遞至磨拋執(zhí)行器的磨拋功能模塊造成的能量損失。

滾珠絲杠螺母副運(yùn)動(dòng)傳遞規(guī)律公式為

式中，l代表滾珠絲杠的導(dǎo)程。

將式（2）代入磨拋執(zhí)行器動(dòng)力學(xué)方程得：

令I(lǐng)=ml/η，τf=fl/η，τext=Fextl/η，則式（4）轉(zhuǎn)變?yōu)?/p>

由于機(jī)器人柔順磨拋執(zhí)行器的結(jié)構(gòu)簡(jiǎn)單，同時(shí)方便拆卸，因此通過(guò)解體稱重的方式獲得磨拋執(zhí)行器的動(dòng)力學(xué)模型參數(shù)，磨拋執(zhí)行器的磨拋功能模塊硬件組件的質(zhì)量數(shù)據(jù)如表1所示。

表1 磨拋功能模塊硬件組件的質(zhì)量 kg

2 基于阻抗模型的柔順控制算法

對(duì)于磨拋執(zhí)行器與葉片之間的法向接觸力的大小，可以通過(guò)適當(dāng)調(diào)節(jié)磨拋執(zhí)行器在葉片型面法線方向的位置來(lái)調(diào)節(jié)。常用的一種方法是根據(jù)磨拋執(zhí)行器感知到的接觸力來(lái)調(diào)整自動(dòng)化設(shè)備的位置，從而動(dòng)態(tài)調(diào)節(jié)磨拋執(zhí)行器與接觸物體之間的接觸力。實(shí)現(xiàn)力的控制有兩種方法：一是基于位置的阻抗控制；另外一個(gè)則是基于力矩的阻抗控制。本文主要研究基于位置的阻抗控制策略。

基于位置的阻抗控制算法的實(shí)現(xiàn)過(guò)程如下：首先采用離線的方式規(guī)劃出設(shè)備的參考軌跡x0，由自動(dòng)化設(shè)備的位置控制環(huán)實(shí)現(xiàn)對(duì)參考軌跡的追蹤。在追蹤離線編程軌跡的同時(shí)，采用阻抗控制算法將設(shè)備與外界的接觸力信息Fext與期望接觸力Fd之間的差值轉(zhuǎn)換為自動(dòng)化設(shè)備的軌跡修正量Xa：

在下一個(gè)位置控制周期內(nèi)，由自動(dòng)化設(shè)備的位置控制環(huán)追蹤經(jīng)過(guò)修正后的軌跡信息xd=x0-xa。因此，這種控制模式是通過(guò)位置伺服控制內(nèi)環(huán)及阻抗力控制外環(huán)的結(jié)合來(lái)實(shí)現(xiàn)的。這種阻抗控制方法容易在現(xiàn)有的大多數(shù)位置控制系統(tǒng)的自動(dòng)化設(shè)備上實(shí)現(xiàn)。基于位置的阻抗控制實(shí)現(xiàn)框圖如圖2所示。

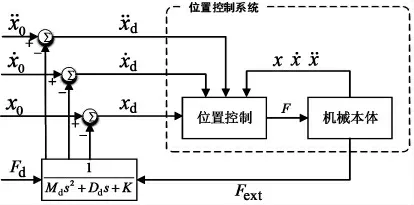
圖2 基于位置的阻抗控制框圖

基于位置的阻抗控制算法的力控制外環(huán)實(shí)現(xiàn)過(guò)程如下：

接下來(lái)對(duì)基于位置的阻抗控制算法的內(nèi)環(huán)位置控制環(huán)展開(kāi)介紹。針對(duì)位置控制環(huán)的開(kāi)環(huán)運(yùn)動(dòng)方程，即上文推導(dǎo)出的機(jī)器人磨拋執(zhí)行器的動(dòng)力學(xué)方程式（7）。

將內(nèi)環(huán)位置控制環(huán)的控制規(guī)律分為基于模型的控制部分和伺服控制部分等2個(gè)部分。基于模型的控制部分的表達(dá)式為

式中，α和β為常數(shù)或函數(shù)。如果將τ′作為新的系統(tǒng)輸入，那么可選擇α和β是系統(tǒng)簡(jiǎn)化為單位慣量構(gòu)成的系統(tǒng)。對(duì)于這種控制規(guī)律結(jié)構(gòu)，系統(tǒng)方程為

因此，為了在τ′輸入下將系統(tǒng)簡(jiǎn)化為單位慣量，系統(tǒng)中的α和β選擇如下；

對(duì)上述條件進(jìn)行整合后可得

式（10）是一個(gè)單位慣量的運(yùn)動(dòng)方程，可以作為被控系統(tǒng)的開(kāi)環(huán)動(dòng)力學(xué)方程。根據(jù)離線編程生成的任務(wù)軌跡θ0（t）及經(jīng)過(guò)柔順控制算法計(jì)算出的軌跡修正量θa（t），得到了經(jīng)過(guò)柔順后的期望軌跡θd（t）。所以軌跡生成器在任意時(shí)間t都會(huì)有一組θ¨d、θ˙d、θd，定義e=θd－θ為期望軌跡與實(shí)際估計(jì)之差。因此機(jī)器人柔順磨拋執(zhí)行器的基于位置的阻抗控制系統(tǒng)內(nèi)環(huán)位置追蹤環(huán)控制框圖如圖3所示。

圖3 位置控制環(huán)框圖

由伺服控制規(guī)律得出的軌跡方程為

將式（13）與單位慣量運(yùn)動(dòng)方程聯(lián)立后可得

對(duì)機(jī)器人磨拋執(zhí)行器浮動(dòng)功能模塊的工作過(guò)程及運(yùn)動(dòng)傳遞過(guò)程進(jìn)行分析，確定伺服電動(dòng)機(jī)控制參數(shù)。磨拋執(zhí)行器力感知功能模塊工作過(guò)程為：當(dāng)推動(dòng)打磨模塊轉(zhuǎn)接板時(shí)，會(huì)對(duì)滑動(dòng)拖板與磨拋功能模塊轉(zhuǎn)接板之間的4個(gè)傳感器產(chǎn)生擠壓或者拉伸變形，從而產(chǎn)生力信號(hào)。力傳感器輸出的電壓信號(hào)被送到信號(hào)放大器，在放大處理之后傳遞給數(shù)字采集卡。由上位PC機(jī)調(diào)用數(shù)字采集卡的三方庫(kù)接收經(jīng)過(guò)信號(hào)放大器處理后的傳感器檢測(cè)信號(hào)。

柔順浮動(dòng)功能模塊的運(yùn)動(dòng)傳遞過(guò)程為：伺服電動(dòng)機(jī)通過(guò)聯(lián)軸器帶動(dòng)滾珠絲杠副轉(zhuǎn)動(dòng)，滾珠絲桿螺母副的螺母與安裝在滑動(dòng)拖板上的螺母座之間緊固連接。其中運(yùn)動(dòng)傳遞過(guò)程中伺服電動(dòng)機(jī)的轉(zhuǎn)速n與滑動(dòng)拖板的移動(dòng)速度v之間的關(guān)系為v=nl，l為滾珠絲杠的導(dǎo)程。

伺服電動(dòng)機(jī)速度控制輸入信號(hào)模擬量電壓與伺服電動(dòng)機(jī)轉(zhuǎn)速之間的關(guān)系如下：伺服電動(dòng)機(jī)最大輸入電壓為+12 V，+6 V對(duì)應(yīng)的是伺服電動(dòng)機(jī)的額定轉(zhuǎn)速3000 r/min。其中伺服電動(dòng)機(jī)的輸入電壓信號(hào)與運(yùn)動(dòng)控制卡輸出的DAC量值之間的對(duì)應(yīng)關(guān)系為：0～10 V對(duì)應(yīng)0～32 767。因此假設(shè)控制的電動(dòng)機(jī)轉(zhuǎn)速為n，伺服電動(dòng)機(jī)速度控制輸入信號(hào)模擬量電壓為V，對(duì)應(yīng)的輸入DAC值為：

調(diào)用運(yùn)動(dòng)控制卡的三方庫(kù)修改DAC的數(shù)值，即可修改伺服電動(dòng)機(jī)的轉(zhuǎn)速，完成了柔順浮動(dòng)功能模塊的伺服電動(dòng)機(jī)的調(diào)速工作。

綜合以上基于位置的阻抗控制算法的力控制外環(huán)及位置控制內(nèi)環(huán)，機(jī)器人柔順磨拋執(zhí)行器的控制系統(tǒng)框圖如圖4所示。

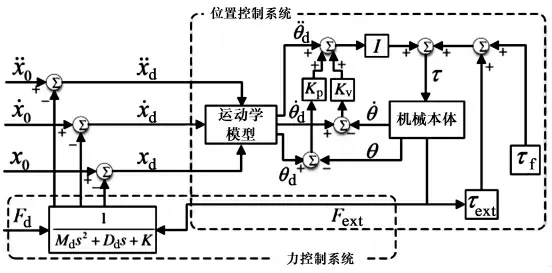
圖4 機(jī)器人柔順磨拋執(zhí)行器控制系統(tǒng)框圖

3 系統(tǒng)穩(wěn)定性分析與模型參數(shù)整定

接下來(lái)利用李雅普諾夫第二方法對(duì)上文中提到的基于位置的磨拋執(zhí)行器控制系統(tǒng)的穩(wěn)定性進(jìn)行分析，同時(shí)利用自動(dòng)控制系統(tǒng)相關(guān)的知識(shí)針對(duì)磨拋執(zhí)行器設(shè)計(jì)的控制系統(tǒng)進(jìn)行控制性能分析。

3.1 李雅普洛夫第二方法

系統(tǒng)的穩(wěn)定性是系統(tǒng)的重要考核指標(biāo)之一，李雅普諾夫?qū)τ谙到y(tǒng)穩(wěn)定性的判定提出了兩種方法：李雅普諾夫第一方法稱為間接法，第二方法稱為直接法。前者通過(guò)求解系統(tǒng)微分方程，根據(jù)其解的特性來(lái)判斷系統(tǒng)的穩(wěn)定性，但由于系統(tǒng)微分方程建立的難度較大，同時(shí)復(fù)雜系統(tǒng)微分方程求解的難度系數(shù)也相對(duì)較大，所以李雅普諾夫第一方法的應(yīng)用受到了極大的限制。本文采用李雅普諾夫第二方法。

李雅普諾夫函數(shù)是一個(gè)表征系統(tǒng)能量的函數(shù)，被記為V（x，t）。這個(gè)函數(shù)與系統(tǒng)的位置x1、x2、…、xn及時(shí)間t有關(guān)。物理系統(tǒng)的能量衰減特性采用能量函數(shù)的導(dǎo)數(shù)V˙（x，t）進(jìn)行表述。所以李雅普諾夫第二方法是從能量的角度判斷系統(tǒng)穩(wěn)定性，分析過(guò)程如下：首先構(gòu)造系統(tǒng)的能量函數(shù)，然后根據(jù)能量函數(shù)的特性及描述能量耗散函數(shù)的特性來(lái)進(jìn)行系統(tǒng)的穩(wěn)定性分析。因?yàn)橹苯臃ú恍枰獙?duì)系統(tǒng)的微分方程進(jìn)行求解，因此在某種程度上降低了復(fù)雜系統(tǒng)穩(wěn)定性判斷的難度，同時(shí)直接法相對(duì)簡(jiǎn)單，所以受到控制系統(tǒng)設(shè)計(jì)領(lǐng)域的學(xué)者青睞，并被廣泛使用。

李亞普諾夫第二方法中提出：對(duì)于一個(gè)定常系統(tǒng)x˙=f（x），t≥0，其中f（0）=0，如果該系統(tǒng)的能量函數(shù)V（x，t）的一階導(dǎo)函數(shù)V˙（x，t）存在而且連續(xù)，且V（0，t）=0，并且對(duì)于系統(tǒng)的狀態(tài)空間X中的一切非零點(diǎn)x滿足以下條件：1）V（x，t）為正定；2）V˙（x，t）為負(fù)定；3）當(dāng)‖x‖→∞時(shí)V（x，t）→∞。

按照李雅普諾夫理論得到結(jié)論，該系統(tǒng)為大范圍漸進(jìn)穩(wěn)定性的定常系統(tǒng)。

柔順磨拋執(zhí)行器的控制系統(tǒng)是由基于位置的阻抗控制的力控制外環(huán)及位置追蹤控制內(nèi)環(huán)組成。本文采用的是運(yùn)動(dòng)控制卡實(shí)現(xiàn)位置追蹤功能，因此磨拋執(zhí)行器的控制系統(tǒng)的內(nèi)環(huán)位置追蹤環(huán)是穩(wěn)定的。本文接下來(lái)主要分析的是基于位置的阻抗控制的力控制外環(huán)的穩(wěn)定性，如果外環(huán)是穩(wěn)定的，則機(jī)器人柔順磨拋執(zhí)行器的控制系統(tǒng)即為穩(wěn)定控制系統(tǒng)。

基于位置控制的阻抗控制系統(tǒng)的力控制外環(huán)的傳遞函數(shù)為

因此控制系統(tǒng)外環(huán)的微分方程為

下面對(duì)該微分方程進(jìn)行求解，為減少振蕩，針對(duì)該二階系統(tǒng)設(shè)計(jì)過(guò)阻尼的響應(yīng)形式，所以Δ=D2-4KM＞0。該非齊次線性微分方程對(duì)應(yīng)的特征方程的根計(jì)算結(jié)果λ1、λ2如下所示：

該微分方程的初始條件即系統(tǒng)的初始狀態(tài)，即當(dāng)t=0時(shí)，x（t）=0，v（t）=0。計(jì)算該非齊次線性微分方程的特解：

根據(jù)李雅普諾夫第二方法，設(shè)定能量函數(shù)為

因此當(dāng)t=0時(shí)，V（t）=0；當(dāng)t≠0時(shí)，V（t）≥0。因此V（t）為正定。

由于λ1、λ2＜0，因此當(dāng)t≠0時(shí)，V˙（t）≤0，因此V˙（t）為負(fù)定。由李雅普諾夫第二方法可知控制系統(tǒng)是穩(wěn)定的。

3.2 模型參數(shù)整定

為方便對(duì)系統(tǒng)動(dòng)態(tài)性能進(jìn)行分析，在自由空間內(nèi)（即機(jī)器人磨拋執(zhí)行器沒(méi)有與外界發(fā)生接觸）時(shí)，將磨拋執(zhí)行器近似簡(jiǎn)化成為一個(gè)具有質(zhì)量彈簧并且有阻尼的物理系統(tǒng)。當(dāng)磨拋執(zhí)行器到達(dá)任務(wù)工作區(qū)且與外界環(huán)境之間發(fā)生接觸時(shí)，此時(shí)將與磨拋執(zhí)行器相接觸的物體簡(jiǎn)化成為一個(gè)剛度為Ke的輕質(zhì)彈簧，簡(jiǎn)化模型如圖5所示。

圖5 接觸狀態(tài)模型簡(jiǎn)化圖

機(jī)器人磨拋執(zhí)行器與外界環(huán)境發(fā)生穩(wěn)定性接觸的運(yùn)動(dòng)過(guò)程如下：首先，在初始t0時(shí)刻，此時(shí)磨拋執(zhí)行器沒(méi)有受到外界作用力，因此根據(jù)基于位置的阻抗控制算法，磨拋執(zhí)行器在期望磨拋力Fd的作用下會(huì)向初始平衡位置A點(diǎn)運(yùn)動(dòng)；當(dāng)磨拋執(zhí)行器與外界物體發(fā)生接觸時(shí)，記為t1時(shí)刻。此時(shí)由于受到了外界剛度為Ke的物體干擾，磨拋執(zhí)行器會(huì)在反饋回來(lái)的實(shí)際作用力Fext與期望力之間的差值的驅(qū)動(dòng)下運(yùn)動(dòng)到新的平衡位置B點(diǎn)。選取機(jī)器人磨拋執(zhí)行器與外界物體發(fā)生接觸的一瞬間，記為初始時(shí)刻t=0，則整個(gè)機(jī)器人磨拋執(zhí)行器與外界環(huán)境發(fā)生穩(wěn)定性接觸過(guò)程的運(yùn)動(dòng)微分方程可以描述為：

第一，執(zhí)行依據(jù)不明確并不是當(dāng)事人造成的，很大程度上的原因應(yīng)該歸咎于人民法院，是其生產(chǎn)了不合格的產(chǎn)品(執(zhí)行依據(jù))。如果執(zhí)行依據(jù)不明確的法律后果是不予立案的話，無(wú)疑是讓當(dāng)事人來(lái)承擔(dān)執(zhí)行依據(jù)不明確的法律后果，這對(duì)當(dāng)事人來(lái)說(shuō)是不公平的。

當(dāng)x（t）＞l時(shí)，

當(dāng)x（t）≤l時(shí)，

在系統(tǒng)的初始狀態(tài)時(shí)x（0）=0，x˙（0）=0。當(dāng)磨拋控制器與環(huán)境接觸的時(shí)刻，即x（t）≤l時(shí)，對(duì)上述方程整理可得

對(duì)應(yīng)的特征方程為

它的兩個(gè)特征根為：

該方程對(duì)應(yīng)的特解為

該微分方程的通解如下：

1）當(dāng)與機(jī)器人磨拋執(zhí)行器相接觸的物體剛度很小的時(shí)候，即Ke比較小，此時(shí)D2-4（Kp+Ke）M＞0。則微分方程的通解為

由于對(duì)應(yīng)的λ1、λ2＜0。因此系統(tǒng)最終收斂至初始位置x（0）=0其收斂速度主要取決于特征值的大小（即D和M）。

2）當(dāng)與機(jī)器人磨拋執(zhí)行器相接觸的物體剛度很大的時(shí)候，即Ke比較大，此時(shí)D2-4（Kp+Ke）M＜0，則λ=α+iβ。其中：

因此該微分方程的通解為

通過(guò)微分方程的解可以看出，接觸的物體剛度較大，系統(tǒng)會(huì)出現(xiàn)振蕩的過(guò)程。不難看出，當(dāng)α的絕對(duì)值越大時(shí)，系統(tǒng)衰減的速度越快，系統(tǒng)收斂到穩(wěn)定狀態(tài)的速度也越快。

綜上所述，與機(jī)器人磨拋執(zhí)行器相接觸的物體剛度很大時(shí)，需要通過(guò)調(diào)整參數(shù)D和M，增大α絕對(duì)值的同時(shí)降低β絕對(duì)值。要使得α絕對(duì)值增加，可以增加系統(tǒng)阻尼系數(shù)D或減小質(zhì)量系數(shù)M；要使得β絕對(duì)值減小，可以增大D值、減小系統(tǒng)彈簧系數(shù)Kp值或者增大M值。一般物理系統(tǒng)的質(zhì)量系數(shù)M是定值，所以通過(guò)調(diào)節(jié)系統(tǒng)的阻尼參數(shù)來(lái)調(diào)節(jié)α與β。與機(jī)器人柔順磨拋執(zhí)行器接觸的機(jī)器人剛度為Ke=5，根據(jù)二階系統(tǒng)的控制參數(shù)整定方法，同時(shí)根據(jù)以上分析，確定基于位置的阻抗控制模型參數(shù)，如表2所示。

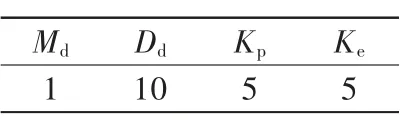
表2 基于位置的阻抗控制模型參數(shù)表

4 仿真結(jié)果與分析

在Windows系統(tǒng)PC機(jī)上，基于C++語(yǔ)言，利用QT設(shè)計(jì)了現(xiàn)場(chǎng)工程師與葉片磨拋設(shè)備之間進(jìn)行數(shù)據(jù)與指令交互的操作軟件，在操作軟件中集成本文設(shè)計(jì)的機(jī)器人柔順控制系統(tǒng)。航空發(fā)動(dòng)機(jī)葉片以壓氣機(jī)葉片為例，其主要特征包括葉盆、葉背、葉緣、安裝板、葉身與安裝板之間的轉(zhuǎn)接圓角及榫頭。

4.1 試驗(yàn)平臺(tái)搭建

航空發(fā)動(dòng)機(jī)葉片的磨拋加工過(guò)程順序如下：葉片裝夾→工具工件坐標(biāo)系標(biāo)定→利用磨拋設(shè)備對(duì)葉片葉背進(jìn)行粗磨→利用磨拋設(shè)備對(duì)葉片葉盆進(jìn)行粗磨→利用磨拋設(shè)備對(duì)葉片進(jìn)氣邊進(jìn)行粗磨→利用磨拋設(shè)備對(duì)葉片排氣邊進(jìn)行粗磨→更換目數(shù)更高的細(xì)砂帶→按同樣的順序進(jìn)行精拋→磨拋完成→卸載葉片。面向航空發(fā)動(dòng)機(jī)葉片磨拋搭建的機(jī)器人磨拋加工實(shí)驗(yàn)驗(yàn)證平臺(tái)如圖6所示。

圖6 機(jī)器人磨拋加工實(shí)驗(yàn)驗(yàn)證平臺(tái)

4.2 葉片磨拋加工驗(yàn)證

從葉片表面質(zhì)量來(lái)看，進(jìn)行磨拋加工之前的葉片型面表面存在著上一步葉片銑削加工留下的銑削刀紋。在采用自主設(shè)計(jì)的磨拋執(zhí)行器對(duì)葉片進(jìn)行磨拋加工之后，葉片型面的銑削刀紋不僅完全被去除，同時(shí)葉片型面邊緣的進(jìn)排氣邊區(qū)域沒(méi)有出現(xiàn)過(guò)磨的現(xiàn)象，葉片表面型面完整度好，不存在手工磨拋出現(xiàn)的接刀痕，型面一致性好。而且磨拋加工之后的葉片葉盆部位的表面粗糙度為Ra0.26 μm，葉背部位的表面粗糙度為Ra0.3 μm，均滿足葉片磨拋加工表面粗糙度Ra0.4 μm以內(nèi)；葉片型面輪廓度磨拋加工精度為-0.03～0.05 mm，滿足葉片磨拋加工型面尺寸要求的-0.05～0.05 mm，接下來(lái)以葉背磨拋為例介紹具體實(shí)驗(yàn)結(jié)果。

首先進(jìn)行葉片磨拋加工路徑規(guī)劃，利用機(jī)器人離線編程軟件InteRobot生成航空發(fā)動(dòng)機(jī)葉片葉背的磨拋加工路徑，磨拋路徑規(guī)劃參數(shù)如表3所示，磨拋路徑展示如圖7所示。

表3 葉背磨拋路徑規(guī)劃參數(shù)表

圖7 葉背磨拋路徑示意圖

針對(duì)航空發(fā)動(dòng)機(jī)葉片葉背的磨拋工藝參數(shù)如表4所示。

表4 葉背磨拋工藝參數(shù)表

葉片葉背磨拋加工過(guò)程中實(shí)際接觸力如圖8所示，實(shí)際接觸力的最大值為1.433 N，最小值為1.359 N。

經(jīng)檢測(cè)，葉片經(jīng)數(shù)控機(jī)床銑削之后，葉背表面布滿著密集的銑削刀紋，經(jīng)過(guò)磨拋加工之后的葉片表面光滑平整，沒(méi)有出現(xiàn)明顯的接刀痕跡，表面質(zhì)量及型面尺寸均滿足葉片磨拋工藝需求。驗(yàn)證了本文提出的磨拋執(zhí)行器柔順控制方法的可行性。

5 結(jié)論

本文采用基于位置的阻抗控制算法及控制規(guī)律分解的系統(tǒng)設(shè)計(jì)方法，設(shè)計(jì)了磨拋執(zhí)行器的柔順控制系統(tǒng)，基于阻抗控制算法及力傳感系統(tǒng)建立力控制外環(huán)，基于動(dòng)力學(xué)模型、伺服單元及運(yùn)動(dòng)控制卡建立了位置控制內(nèi)環(huán)，實(shí)現(xiàn)了機(jī)器人柔順磨拋執(zhí)行器對(duì)外界接觸力的柔順響應(yīng)；最后利用李雅普諾夫第二方法分析了磨拋執(zhí)行器的控制系統(tǒng)運(yùn)行的穩(wěn)定性，提高了系統(tǒng)穩(wěn)定性，可確保葉片磨拋加工過(guò)程中磨拋力的穩(wěn)定性。以壓氣機(jī)葉片為對(duì)象進(jìn)行實(shí)驗(yàn)，通過(guò)對(duì)葉背磨削前后參數(shù)進(jìn)行對(duì)比，驗(yàn)證本文所提出的柔順控制算法能夠?qū)崿F(xiàn)提高葉片表面磨拋加工質(zhì)量及葉片型面尺寸精度的目的。