考慮加班的無拖期作業車間調度問題多目標金鷹優化算法研究

史雙元 熊禾根

武漢科技大學機械自動化學院,武漢,430081

0 引言

制造系統優化調度是實現制造資源優化利用和提高生產運作效率的重要和關鍵技術之一。在諸多的制造系統優化調度目標中,對于面向訂單型制造企業,滿足客戶訂單的交貨期是最重要的目標之一。然而,由于企業內部生產能力相對穩定與外部訂單任務隨機性之間的矛盾,當制造系統負荷率較高時,常規工作時間的生產作業可能導致某些訂單的拖期交貨,進而造成因拖期懲罰而帶來的經濟損失和影響企業商譽。為了盡可能避免上述不利情況的發生,企業管理者通常在采用生產優化調度的同時,通過加班作業的方式擴充常規生產能力,從而盡力保證訂單無拖期交貨。顯然,一方面,加班作業可以擴充生產能力,但另一方面也會產生額外的生產費用。如若加班作業在時間和資源對象上安排不恰當不合理,可能不但無法有效和針對性地提前訂單的完成時間,還會增加企業生產成本。如何將加班作業與優化調度進行融合,從而實現企業損失的最小化和效益的最大化,是面向訂單型企業生產運作管理亟待解決的重要問題。為此,本文提出了一種考慮加班作業的多目標無拖期作業車間調度問題(multi-objective no-tardiness job shop scheduling problem with overtime consideration,MONTJSSP/O),以期通過問題的研究,在生產負荷較重但處于有限范圍內的狀況下,充分和優化地利用加班作業,從而實現訂單的無拖期交貨。

MONTJSSP/O問題的關鍵特征在于無拖期交貨和考慮加班作業。在大量與拖期有關的作業車間調度問題研究中,絕大多數研究對問題進行數學建模時,將交貨期考慮在優化的目標函數中,如最小化(加權)總拖期和/或總提前、最小化最大拖期、最小化(加權)拖期工件數量等[1-5]。這些研究只是降低了拖期程度,并不能保證訂單的無拖期交付。現有研究中,在作業車間調度問題中考慮無拖期約束的研究尚未見到,與無拖期相關的調度問題研究報道也比較少,且基本是針對單機調度問題[6-8]的。CHAND等[6]針對無拖期單機調度問題,以總加權提前量為優化目標,設計了精確算法和近似方法進行求解;ZHAO等[7]分析了具有劣化作業(即工件加工時間隨著開工時間線性遞減)的單機調度問題,在滿足無拖期工件的前提下,提出了以最小化總提前懲罰為目標的優化算法。加班作業是制造企業應對客戶需求激增常采用的一種短期擴大產能的方法[9-10]。查閱已有文獻發現,針對作業車間調度問題,通過加班作業擴大產能的研究不是很多。ZHANG等[11]通過加班作業提高產能,以單機調度問題研究了無拖期交付的問題。HOLLOWAY等[9]提出了一種考慮工件交貨期和加班作業的靜態和動態作業車間調度問題解決方法,以找出加班與總拖期之間的關系。YODA等[12]通過在每個常規班次中延長加班時間來調整產能,并以最小化總拖期和總加班時間為優化目標。上述文獻或者不是基于作業車間調度問題進行的研究,或者不是真正意義上的無拖期交付。

問題求解方面,本文提出了基于精英保留策略的非支配排序金鷹優化算法(elitist non-dominated sorting golden eagle optimizer,NSGEO)。金鷹優化算法(golden eagle optimizer,GEO)是一種基于群體的新型智能優化算法[13]。自GEO算法被提出以來,已被應用于諸多領域[14-17]。針對多目標問題,MOHAMMADI-BALANI等[13]擴展單目標GEO算法提出了多目標金鷹優化算法,在10個標桿測試函數上對算法性能進行了測試和驗證,結果表明所提算法的性能優于其他用于對比的常見多目標算法(包括多目標灰狼算法、帶精英保留策略的非支配排序遺傳算法、多目標粒子群算法、多目標樽海鞘群算法)。從上述文獻中可以看出,多目標金鷹優化算法在求解多目標優化問題時能表現出較好的性能。

綜上所述,本文研究的創新點主要體現在:①已有拖期相關作業車間調度問題研究主要將拖期作為目標函數,以實現訂單拖期的最小化,本研究將訂單無拖期交付作為問題約束,構建了相應的數學規劃模型;②在調度時間域上設置加班時間區間,以區別常規工作時間,進而采用加班作業擴大常規生產能力,通過優化調度實現訂單無拖期交付;③關于多目標金鷹優化算法的研究主要側重于連續多目標優化問題的求解,本研究通過有效的編碼和解碼設計將其用于求解無拖期作業車間調度組合優化問題,并通過仿真調度實驗驗證了算法的有效性和優越性能。

1 MONTJSSP/O問題描述與建模

1.1 MONTJSSP/O問題描述

所提MONTJSSP/O問題可描述如下:有n個獨立的待加工工件和m臺可用機器;每個工件都有若干道具有工藝約束的工序,每道工序需要在一臺事先確定的機器上加工,且加工時間已知;每個工件都有嚴格的交貨期;在整個計劃時間區間內,除了常規的工作時間外,還有一些可拓展使用的時間片段(加班時間);若加班時間被利用,則將產生額外的生產成本;工件交貨期不能處于加班時間區間。問題求解目標是優化安排加班時間,確定各工序的加工順序和開工時間,從而使完成所有工件的工期和總加班時間最小。

此外,MONTJSSP/O問題還遵從以下假設條件:①所有工件和機器零時刻可用;②不單獨考慮裝設時間和轉序時間;③同一時刻下,每臺機器只能加工一個工件,每個工件只能被一臺機器加工;④工件的加工過程不允許被中斷,即不允許工時拆分,不允許被搶占;⑤工件間相互獨立,且不存在優先級關系;⑥不考慮機器故障、訂單變化和急件插入等動態事件;⑦所有加班時間區間內的單位時間加班成本相同;⑧工件的交貨期設置合理,考慮加班作業情況下不至于絕對超負荷。其中,假設①～⑥是研究作業車間調度問題的基本假設[1-4,18];假設⑦主要是為了簡化加班成本的計算;假設⑧約定了本研究適用范圍,如果交貨期設置不合理,則存在不使用加班作業也能實現無拖期交付,或者使用所有加班時間也無法實現無拖期交付的情況。

1.2 數學模型建立

為了方便建立問題數學模型,定義本文中用到的數學符號如表1所示。

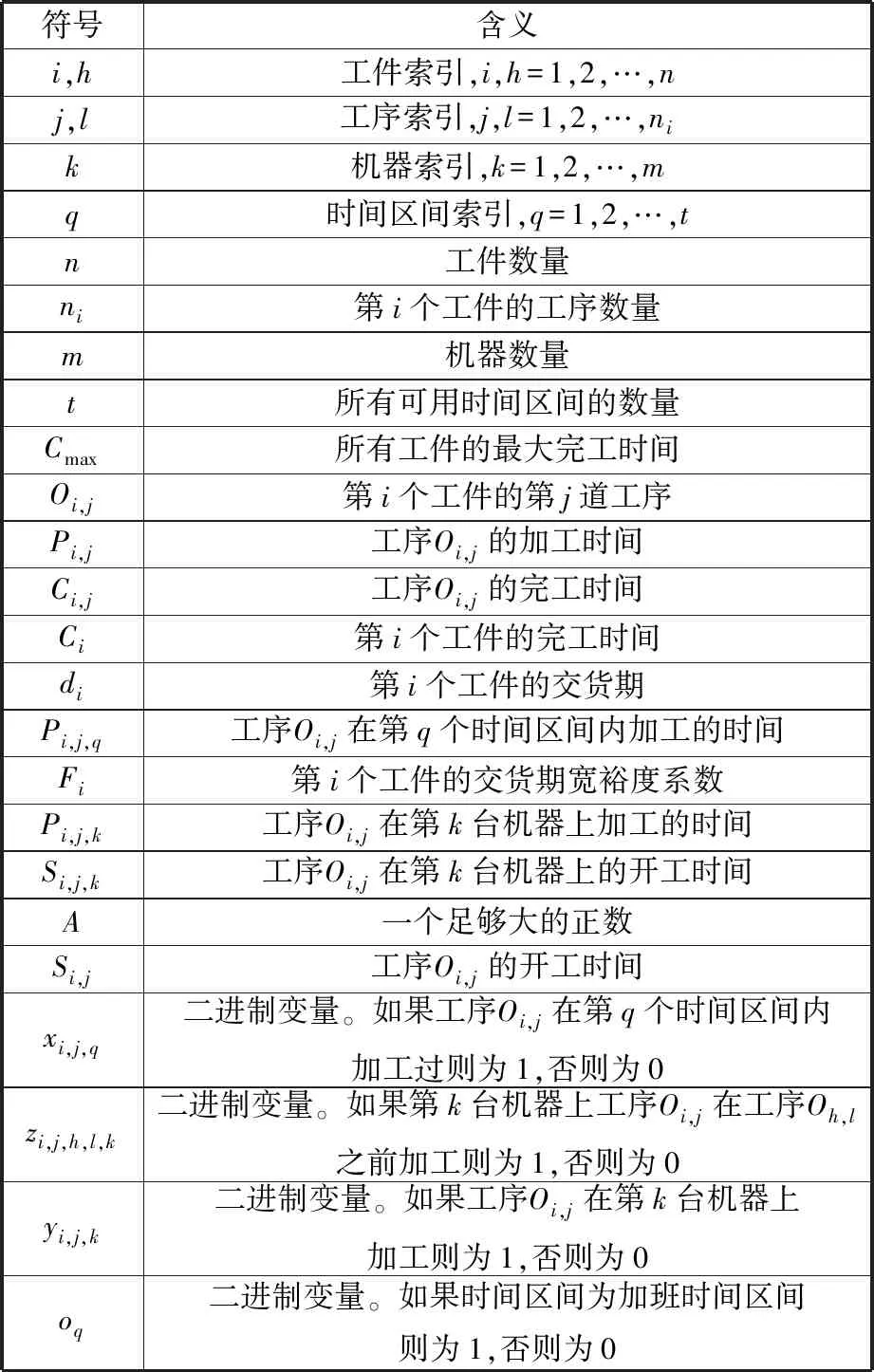
表1 數學符號定義

基于表1所示的符號定義,MONTJSSP/O問題的數學模型可表示如下:

(1)

minf2=Cmax

(2)

滿足約束如下:

Ci-di≤0i=1,2,…,n

(3)

Si,j+Pi,j≤Si,j+1

(4)

i=1,2,…,nj=1,2,…,ni-1

Si,j≥0i=1,2,…,nj=1,2,…,ni

(5)

Si,j+Pi,j=Ci,j

(6)

i=1,2,…,nj=1,2,…,ni

(7)

i=1,2,…,nj=1,2,…,ni

(8)

i=1,2,…,nj=1,2,…,ni

(9)

i=1,2,…,nj=1,2,…,ni

Si,j,k+Pi,j,k≤Sh,l,k+A(1-zi,j,h,l,k)

(10)

i,h=1,2,…,nj,l=1,2,…,ni

k=1,2,…,m

其中,式(1)和式(2)表示兩個目標函數,分別為最小化總加班時間和最小化最大完工時間;式(3)定義無拖期約束;式(4)和式(5)約束一個工件的工序只能在它的緊前工序加工完成后才能開始加工,且開工時間須在零時刻以后;式(6)表示工序一旦開工就不能被中斷;式(7)和式(8)表示工序可在一個或多個時間區間內進行加工,且加工時間等于各時間區間內花費時間的總和;式(9)和式(10)約束一道工序只能在一臺機器上加工,且一臺機器同時只能加工一道工序。

2 算法設計

與傳統作業車間調度問題相比,MONTJSSP/O具有更大的求解難度,主要體現在:①增加了無拖期約束,提高了獲得可行解的難度;②增加了加班時間的優化使用決策。本文以期通過對基本多目標金鷹優化算法[13]進行適應性改造來有效求解MONTJSSP/O問題并獲得優越性能。

基于精英保留策略的非支配排序金鷹優化算法(NSGEO)對基本多目標金鷹優化算法進行了如下改進:①采用離散編碼方式,以實現金鷹優化算法連續空間至MONTJSSP/O離散解空間的映射;②采用兩階段解碼方案,以增加滿足無拖期約束可行解的數量,并盡可能減少最大完工時間和總加班時間;③嵌入基于精英保留策略的非支配排序選擇算子,以加速算法的收斂速度和提高解質量;④引入自適應新個體生成策略,以均衡算法的全局搜索能力和局部尋優能力。NSGEO算法的偽代碼如算法1所示。

算法1 NSGEO算法偽代碼輸入:初始種群Pinit;種群規模Fpop;最大迭代次數Imax;攻擊傾向參數[p(0)a,pmaxa];巡航傾向參數[p(0)c,pmaxc]。輸出:Pareto最優解集(Pbest)。1 設置當前迭代次數g=0;2 for g in Imax do3 設置當前種群個體序號φ=0;4 采用兩階段解碼方案計算所有個體的適應度值;5 對所有個體按適應度值進行非支配排序;6 for φ in Fpop do7 if第φ個個體為精英個體then8 保留該個體不變;9 else10 計算攻擊概率pa和巡航概率pc;11 if pc>pa then ∥ exploration phase12 使用交叉和變異組合操作生成新個體;13 else ∥exploitation phase

2.1 編碼方式

基本多目標金鷹優化算法通常被用于求解連續優化問題。在算法中,金鷹個體根據文獻[13]中式(6)迭代更新自己的位置。由于MONTJSSP/O是離散型優化問題,因此,需要設計有效編碼方法將問題解空間映射至算法空間。受遺傳算法等進化類優化算法啟發,本文采用已廣泛使用的基于工件序號的編碼方式。圖1為2臺機器4個工件的編碼示意圖,案例具體信息如表2所示,其中第1列表示工件序號;第2、3列表示加工信息,圓括號外數字表示工序序號,圓括號內數字表示加工工時;第4列表示各工件交貨期。圖1所示為該案例的一個編碼結果,加工序列中每個基因位上的整數表示工件編號,從左往右,整數編號在加工序列中第j次出現就代表該工件的第j道工序。加工序列的長度為所有工件所有工序數的總和。

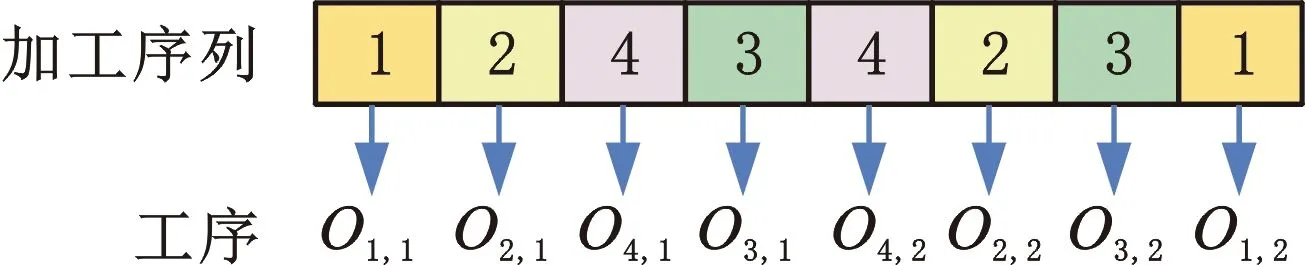
圖1 編碼方式示例

表2 2臺機器和4個工件案例信息

2.2 兩階段解碼方案

以圖1所示的編碼為例,采用傳統解碼方法得到的活動調度解如圖2所示,其中d1、d2、d3、d4分別為工件J1、J2、J3、J4的交貨期,[8,16]表示加班時間區間,最大完工時間Cmax=31。由圖2可以看出,該活動調度解為非法解,工件J1的完工時間(C1=31)超過了其交貨期(d1=23),不滿足無拖期約束。

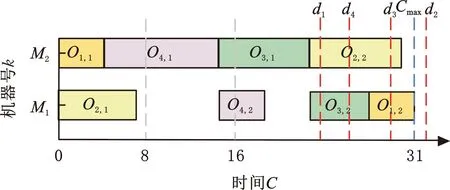
圖2 傳統解碼方式調度結果

為此,本文基于問題特征提出了一種兩階段解碼方案,具體流程如下:

(1)第一階段解碼。該階段旨在讓所有工序盡早開工,使所有工件最大完工時間盡可能地短。圖3所示為第一階段解碼流程。具體方法是:從左往右依次對加工序列上所有基因進行排序,待排工序開工時間需滿足同工件工序間的前后約束關系。加工機器上任何加工間隙如果時間足夠長,則可在該時間段安排加工該工序。如果該機器上有多個時間區間可用,則選擇使用加班時間最少的時間區間。如圖3a所示,待排工序O1,2有三種可排位置,但第②種方案既能滿足工件J1無拖期交付,也能盡量減少加班時間,所以選擇此方案。經過第一階段解碼后的調度結果如圖3b所示。若經過第一階段解碼后的排序結果為非法解(即存在拖期),則刪除該個體,然后隨機生成新個體,并繼續執行第一階段解碼過程,如此循環直至得到可行解。若前述循環過程執行30次后仍未得到可行解,則直接結束當前個體的解碼過程,繼續執行下一個個體的解碼過程。

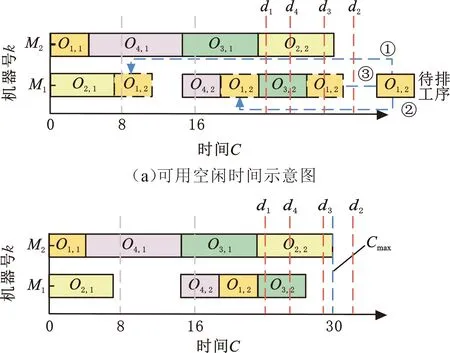
(b)第一階段解碼結果

(2)第二階段解碼。該階段是在第一階段解碼結果的基礎上,保持工件最大完工時間不變,并滿足無拖期約束,將所有工序盡量往右移(推遲工序開工時間),將處于加班時間區間的工序盡量移動至常規工作時間區間,從而減少總加班時間。若某道工序右移后加班時間會增加,則保持工序開工時間不變。如圖4a所示,在第一階段解碼結果的基礎上搜索可以右移的工序。從圖4a中可以看出,在滿足無拖期約束和Cmax不變的情況下,工序O3,2和O1,2可往右移。當工序O3,2和O1,2移動完成后,工序O4,2也可往后移。由此可知,在此階段共有三個工序可往右移,工序O4,2右移后減少了總加班時間。第二階段解碼結果如圖4b所示。

(b)第二階段解碼結果

將兩階段解碼方式和傳統解碼方式得到的解碼結果進行對比可知,通過兩階段解碼方式得到的解碼結果不僅滿足了無拖期約束,而且減少了最大完工時間和總加班時間。由圖2和圖4可以看出,采用傳統解碼方式得到調度解的最大完工時間為31,總加班時間為10;采用兩階段解碼方案得到調度解的最大完工時間為30,總加班時間為9。與傳統解碼方式對比可知,采用兩階段解碼方案使最大完工時間和總加班時間分別減少了1。

2.3 基于精英保留策略的選擇算子

受文獻[19]的啟發,本研究在改進金鷹優化算法中嵌入了基于精英保留策略的選擇算子來選擇種群中表現更優的個體進入下一代:首先通過非支配等級劃分方法按適應度值將種群中所有個體分為若干個非支配等級,然后根據擁擠度距離對同一支配等級下的個體進行排序,最后選擇支配等級低、擁擠度大的個體構造新的種群。基于精英保留策略的選擇算子具體執行步驟如下。

(1)設當前種群為Pnow,種群規模為Fpop,初始化下代種群Pnext為空集。

(2)計算種群Pnow中個體的非支配等級。首先找出Pnow中非支配最優解,構成第一個非支配最優解層,記為R1,然后將R1中個體從Pnow中去除,再從余下個體{Pnow-R1}中找出新的非支配解,記為R2,依次類推,直到所有個體被分級。

(3)對步驟(2)得到的各等級集合Ri(i≥1)分別計算其中每個個體的擁擠度距離,并按照該距離從大到小對其中的個體進行排序。

(4)遍歷當前種群Pnow所有個體,執行如下操作:若當前個體為精英個體(判定依據:種群中所有個體按非支配等級從小到大和各等級中按擁擠度距離從大到小綜合排序,排序位于前Fpop×50%的個體被定義為精英個體),則直接將該個體存入集合Pnext;若不是精英個體,則生成新個體并存入集合Pnext。

2.4 自適應子代個體生成策略

在每次迭代過程中,如果個體不是精英個體,則需要重新生成新個體用于下輪迭代。為了兼顧算法的全局搜索和局部尋優能力,本文引入了自適應個體更新策略,具體步驟如下。

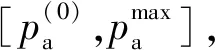
(2)計算當前攻擊概率pa和當前巡航概率pc,其計算表達式分別如下:

(11)

(12)

(3)如果pc>pa,則采用POX交叉[20]和兩點交換變異組合操作生成新個體;否則,使用基于N5鄰域結構的局部搜索[21]方法生成新個體。

基于以上步驟,在迭代初期使用交叉和變異組合操作生成相似度不高的新個體,擴大種群搜索范圍,防止算法陷入局部最優;進入迭代后期時,使用局部搜索產生相似度較高的個體,以提高局部搜索能力。

3 仿真實驗與結果分析

為了驗證NSGEO算法性能,所有算法采用C語言進行編程,并在配置了Intel Core i3 CPU和8G RAM的Windows 10系統中進行了測試。

3.1 算例生成

由于MONTJSSP/O問題不存在標準測試集數據,因此對{FT06、FT10、FT20},{LA01、LA06、LA11、LA16、LA21、LA26、LA31、LA36},{SWV01、SWV06、SWV11、SWV16},{TA01、TA11、TA21、TA31、TA41、TA51、TA61、TA71}共23個作業車間調度問題基準算例進行了改造以滿足本問題的研究。為區別于標準算例,改造后的算例名稱為在原算例名稱前面加上符號m,如mFT06、mLA01、mSWV01和mTA01等。

算例改造體現在時間域的離散化和交貨期的設置這兩方面。時間域的離散化主要指加班時間和常規工作時間區間的設定,具體規則為:每24小時為一個循環周期,每個循環周期包含16小時的常規工作時間和8小時的加班時間,即[0,16]為常規工作時間區間,[16,24]為加班時間區間。工件交貨期采用常用的總工作量(total work content,TWK)規則,具體計算公式為

(13)

式中,i、j分別為工件索引和工序索引,di為第i個工件的交貨期;Fi為第i個工件的交貨期寬裕度系數;Pi,j為第i個工件第j道工序的加工時間。每個工件的交貨期寬裕度系數的取值取決于問題的規模,確定方法將在3.3.1節中介紹。

3.2 性能評價指標

本研究采用三個性能指標來評價算法的優劣性。由于本問題引入了無拖期約束,采用啟發式算法求解時極易產生非法解,而可行解的數量直接影響最優解的好壞,因此本文將可行解數量作為一個評價指標。此外,為了綜合評價多目標算法的收斂性和解的分布性,本文選擇反世代距離(inverted generational distance,IGD)和超體積(hypervolume,HV)兩個常用的多目標評價指標。上述兩個評價指標的計算方法和評價規則可參考文獻[2,5]。

理論上,種群規模和迭代次數的乘積為所有可能解的數量,如種群規模為100,迭代次數為100,則所有可能解的數量為10 000。在問題求解過程中,得到的可行解數量(number of feasible solutions,NFS)越多,則搜索到最優解的可能性越大,表明算法性能越好。

3.3 實驗結果及性能分析對比

為了驗證NSGEO算法求解MONTJSSP/O問題的性能,本節首先驗證了改進項對算法性能的影響,然后將NSGEO算法與其他三種多目標優化算法進行了對比實驗分析。

3.3.1兩階段解碼的性能分析

為了驗證兩階段解碼方案的有效性,使用基本遺傳算法進行了實驗,將求解過程中產生的可行解數量(NFS)作為評價指標。實驗中,設置種群規模為100,迭代次數為100。由于交貨期的設置會直接影響訂單是否能按期交付,因此在不同交貨期寬裕度系數F(F=2,4,6,8)下進行了實驗,實驗結果如表3所示,其中SD列和TD列分別表示通過傳統解碼(standard decoding,SD)方式和兩階段解碼(two-stage decoding,TD)方式實驗后得到的可行解數量。

表3 傳統解碼和兩階段解碼方案下得到的可行解數量對比

從表3中可以發現,在合理F值下,兩階段解碼方案比傳統解碼方式更加有效。比如:F=2時,所有23個測試算例中,通過SD方式只有mFT06算例能得到3個可行解,但TD方式有mFT06、mFT10、mLA16和mLA36共4個算例能得到可行解,且mFT06算例能得到542個可行解;F=4時,通過SD方式只有30%的算例能得到可行解,但通過TD方式有70%的算例能得到可行解,且TD方式得到的可行解數量遠大于SD方式得到的可行解數量;F=8時,所有算例可通過TD方式得到可行解,但通過SD方式還有5個算例未能得到可行解。

通過以上分析可以看出,兩階段解碼方案在得到可行解數量方面是有效的,與傳統解碼方式相比具有很大的優勢。此外,從表3中還可以看出交貨期寬裕度系數對可行解數量的影響很大。若F值過小,可行解數量太少或為零,說明交貨期太緊,無法通過優化實現無拖期;若F值太大,則交貨期太松,與實際生產情況不符。為此,本文以兩階段解碼方案下產生的可行解數目大于50為依據,確定了各測試算例下的交貨期寬裕度系數。顯然,按此方法確定的工件交貨期可滿足本文1.1節中的問題假設⑧。

3.3.2不同配置多目標金鷹優化算法的性能比較

為檢驗NSGEO算法中各項改進對問題求解性能的影響,采用三種不同配置的多目標金鷹優化算法(MOGEO)進行了仿真調度實驗(兩階段解碼方案的有效性在3.3.1節已得到驗證,本節實驗在三種比較算法中均加入兩階段解碼方案)。三種多目標金鷹優化算法的配置情況見表4。

表4 三種多目標金鷹優化算法配置項

為確定較好的算法控制參數,通過田口實驗進行了先導性試驗,所得較優的算法控制參數為:種群規模取100,最大迭代次數取2000,攻擊傾向參數pa取[0.5,2],巡游傾向參數pc取[1,0.5]。

針對所有算例,各算法獨立運行10次,采用IGD、HV兩個評價指標比較算法的性能,對比結果如表5和圖5所示,其中F列表示各改造算例中交貨期寬裕度系數的取值。

(a)IGD均值減小率曲線

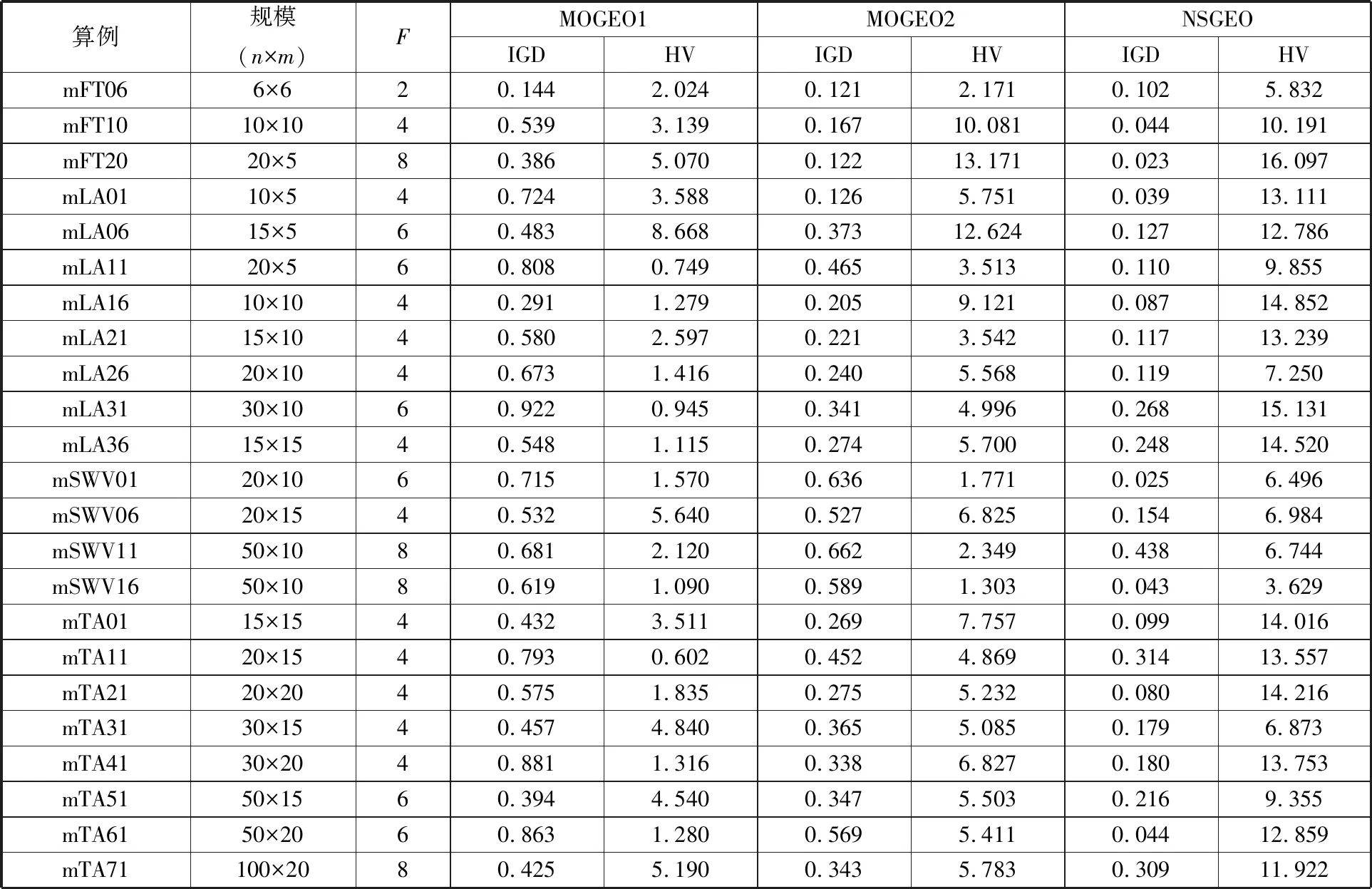
表5 算法改進項有效性分析

通過表5數據和圖5曲線可見:

(1)MOGEO2算法與MOGEO1算法相比,前者得到的IGD均值更小,減小率最大達到了82.5%,如圖5a所示;前者得到的HV均值也更大,56%的算例中HV均值增長率超過100%,如圖5b所示。統計數據表明自適應子代個體生成策略有效地提升了算法性能。

(2)NSGEO算法與MOGEO2算法相比,在23個測試算例中,前者相比于后者有11個算例的IGD均值減小率超過60%,如圖5a所示;14個算例中的HV均值增長率超過100%,如圖5b所示。由此可知,帶精英保留策略的非支配排序選擇算子對算法性能提升很大。

綜合以上分析,各改進項對多目標金鷹優化算法求解MONTJSSP/O問題的性能提升有效,且效果明顯。

3.3.3NSGEO算法與其他多目標優化算法的性能比較

為進一步驗證NSGEO算法求解MONTJSSP/O問題的優越性,本文將NSGEO算法和當前求解多目標優化問題常用的基于分解的多目標進化算法(multi-objective evolutionary algorithm based on decomposition,MOEA/D)[22-23]、帶精英保留策略的非支配排序遺傳算法(non-dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)[21, 24]和混合遺傳禁忌搜索算法(hybrid genetic algorithm-tabu search,HGATS)[18,25]三種算法的性能進行了對比。算法具體參數設置如表6所示。為了保證公平性,四種算法的共有參數設置相同值,種群規模均為100,最大迭代次數均取2000。

表6 對比算法參數設置

本節采用3.2節描述的IGD和HV兩個性能評價指標來對比分析四種算法的性能。表7和表8分別給出了四種算法在每個算例上獨立運行10次后兩個性能指標的均值和標準差,粗體字部分表示均值最佳值。

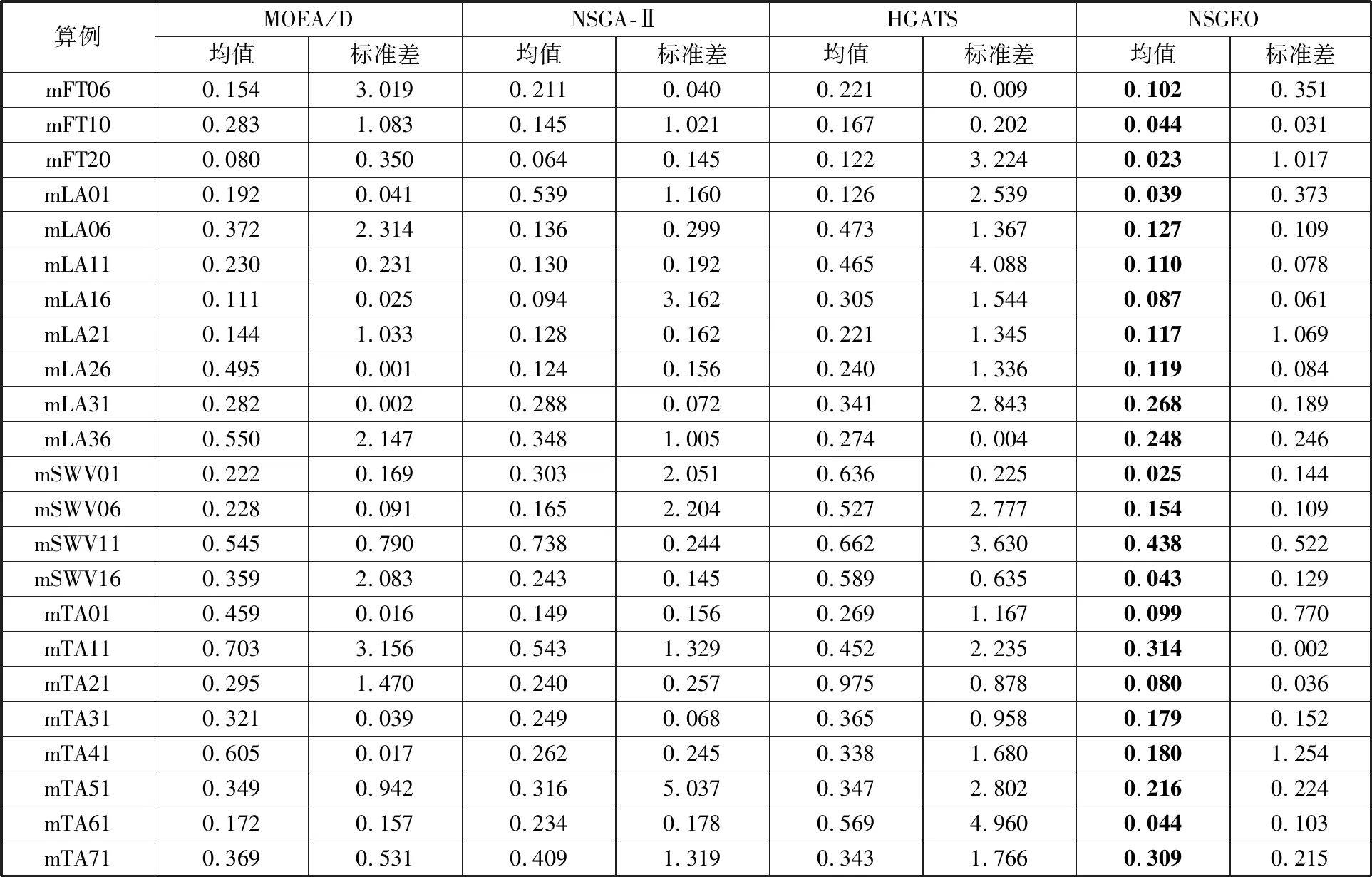
表7 NSGEO、MOEA/D、NSGA-Ⅱ和HGATS四種算法IGD對比

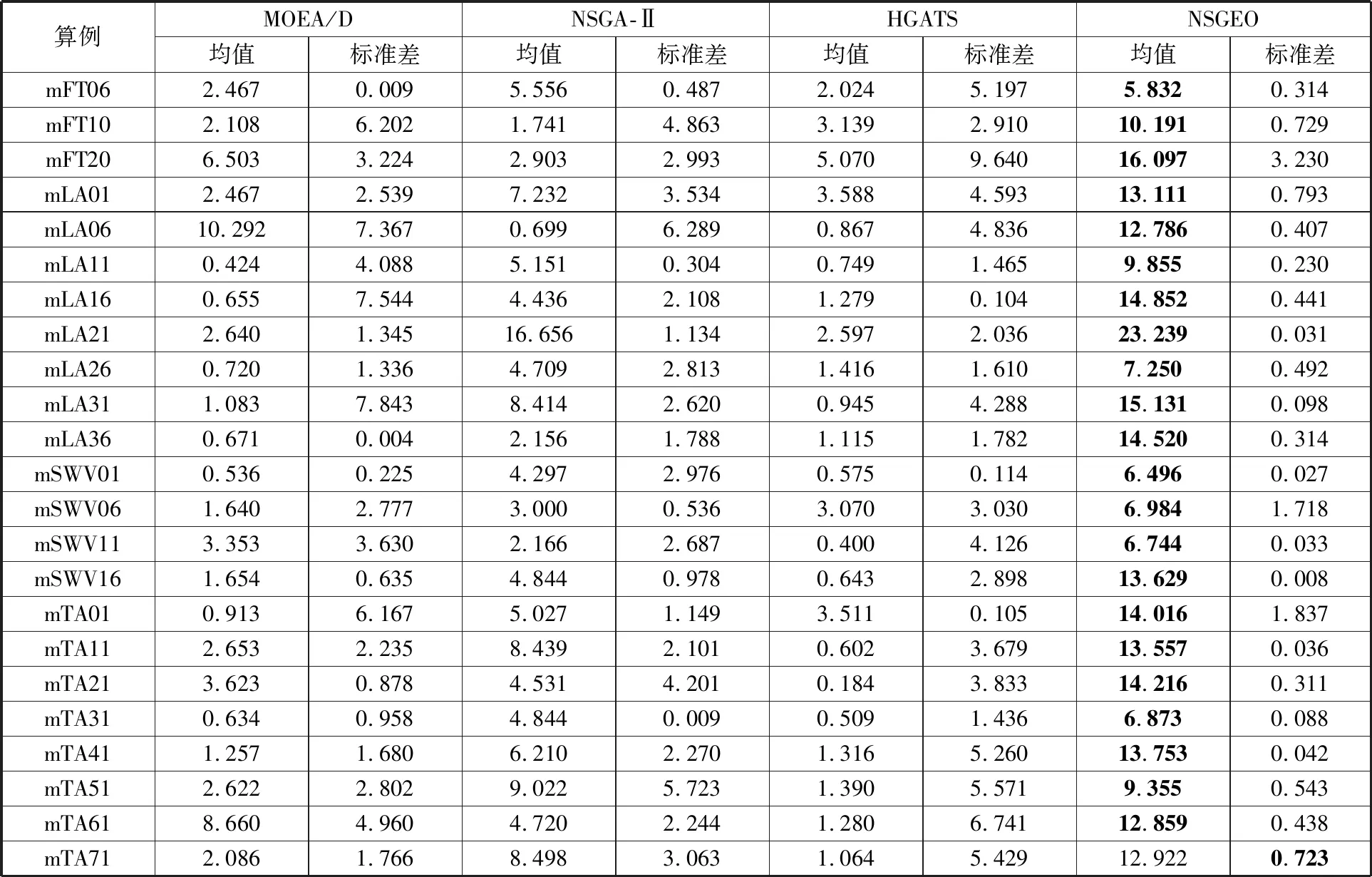
表8 NSGEO、MOEA/D、NSGA-Ⅱ和HGATS四種算法HV對比

表7所示為四種算法得到的IGD指標結果,從表中可以看出,與其他三種算法相比,NSGEO算法在23個測試算例中的IGD均值最小,說明NSGEO算法在所有算例中求解得到的Pareto前沿面與真實Pareto前沿面更加接近,即NSGEO算法所得到解的質量更高。

為更加清楚地展示各測試算例通過不同算法所得到的IGD均值及標準差的分布,圖6給出了四種對比算法得到的IGD均值和標準差分布曲線。從圖6a中可以明顯看出:MOEA/D算法和HGATS算法得到的IGD值比NSGA-Ⅱ算法和NSGEO算法得到的IGD值相對更大;雖然NSGA-Ⅱ算法在56%的算例上得到的IGD值與NSGEO算法對應得到的IGD值相近,但在其他算例上與NSGEO算法相差較大,如mLA01、mSWV11和mTA11。總體來說,對于所有測試算例,NSGEO算法比其他三種算法得到的IGD值更小。此外,從圖6b中可以發現NSGEO算法在大多數測試算例上標準差更小。對于算例mFT20、mLA21、mTA01和mTA41,與MOEA/D算法和NSGA-Ⅱ算法相比,NSGEO算法得到的IGD標準差更大,但該算法得到的IGD均值更小。綜合上述分析,NSGEO算法在IGD評價指標上明顯優于其他三種對比算法,具備更好的收斂性、多樣性和穩定性。

表8和圖7分別展示了四種算法得到的HV指標結果數據以及HV均值和標準差分布曲線。從圖7a中可以看出,NSGEO算法得到的HV均值比其他三種算法得到的HV均值大很多,有近74%的算例增長率超過50%,可見NSGEO算法相較于其他三種算法有明顯的優勢。對于HV標準差,由圖7b可見,少數算例NSGEO算法得到的HV標準差比其他算法得到的HV標準差稍大,但差值并不明顯,總體來看,NSGEO算法得到的HV標準差更小,算例間的波動也較小。從上述分析不難看出,NSGEO算法的HV指標值優勢比較明顯,表明NSGEO算法比其他三種算法得到的解質量更高,性能更加穩定。

(a)HV均值曲線

為比較直觀地觀察到各算法得到的Pareto解集的分布情況,對所選擇的6個不同規模算例某次運行的結果進行了展示,如圖8所示,其中不同形狀的點代表不同算法獲得的解集。從圖8中可以看出,本文研究的兩個目標之間存在沖突關系。從Pareto解集的分布可以定性發現,NSGEO算法得到的Pareto解基本都支配著其他三種算法得到的Pareto解,而其他三種算法得到的Pareto解集之間存在相互支配關系。這種分布說明NSGEO算法得到的Pareto解集更接近真實Pareto前沿,解的質量更優。從解的多樣性來說,對于算例mTA51,雖然NSGEO算法得到的Pareto解集相對于NSGA-Ⅱ算法稍差,但NSGEO算法得到的Pareto解集更接近真實的Pareto前沿,收斂性更好。從實用性角度來看,對于6個展示的算例,NSGEO算法得到的解的個數相對更多,說明供決策者可選擇的方案越多。

(a)mFT20 (b)mLA21 (c)mLA36

綜上所述,NSGEO算法能夠求解本文所提出的問題,并且在求解過程中具備比MOEA/D、NSGA-Ⅱ和HGATS三種算法更好的全局搜索和局部尋優能力。

4 結論

為了有效解決面向訂單型制造企業合理使用加班時間實現無拖期交付的問題,本文以最小化加班時間和最大完工時間為目標建立了問題的數學模型,提出了一種基于精英保留策略的非支配排序金鷹優化算法(NSGEO)對問題進行了求解,得出了以下結論:

(1)通過分析考慮加班作業的多目標無拖期作業車間調度問題(MONTJSSP/O)和基本多目標金鷹優化算法特點,設計了一種離散編碼方式,將金鷹優化算法連續空間映射至問題離散解空間,使問題易于通過啟發式算法進行求解。

(2)與傳統解碼方式進行了對比實驗,結果表明,在合理交貨期設置情況下,本文提出的兩階段解碼方案得到的可行解數量遠大于傳統解碼方式得到的可行解數量,表明采用所提出的解碼方式求解MONTJSSP/O問題是有效的,且效果顯著。

(3)通過比較不同配置下的多目標金鷹優化算法性能可得,基于精英保留策略的非支配排序選擇算子和自適應子代個體生成策略對多目標金鷹優化算法的性能均有顯著提升。

(4)通過比較不同測試算例上的仿真調度實驗和算法,驗證了采用所提NSGEO算法在求解MONTJSSP/O問題時,既保證了算法的收斂性又很好地兼顧了Pareto解集的分布性,而且對解決不同規模問題的穩定性上也明顯優于其他對比算法。

通過加班作業擴充生產能力是保證訂單無拖期交貨的有效措施。然而,若訂單過于密集和交貨期設置太緊,進而使得制造系統負荷超過一定極限時,則需結合其他資源擴展方式以實現訂單的無拖期交付,如機器柔性、工藝柔性和外協加工等。為此,后續可對融合多種可擴展資源的作業車間無拖期調度問題進行進一步的研究。此外,實際制造系統中的調度問題大多屬于動態調度問題,為此,在本文研究基礎上,需對動態作業車間無拖期調度問題進行進一步的相關研究。