半穿式應急鋼桁梁上弦桿面外屈曲臨界力研究

趙 曼,陳士通,孫志星,許宏偉,黃曉明

(1.石家莊鐵道大學 土木工程學院,石家莊 050043;2.石家莊鐵道大學 省部共建交通工程結構力學行為與系統安全國家重點實驗室,石家莊 050043;3.石家莊鐵道大學 大型基礎設施性能與安全省部共建協同創新中心,石家莊 050043;4.石家莊鐵道大學 河北省交通應急保障工程技術研究中心,石家莊 050043;5.東南大學 交通學院,南京 210096)

半穿式鋼桁梁具有構造簡單、拼組快速等特點,使其在橋梁應急搶修時成為應用較為廣泛的橋型之一。但由于半穿式鋼桁梁兩側上弦桿之間沒有橫向聯結系,使用不當可能引發安全事故。19世紀末,半穿式鋼桁梁破壞事故相繼發生[1],為此,國內外學者針對半穿式鋼桁梁面外屈曲問題陸續開展相關研究。Ziemian[2]進行了彈性支撐兩端鉸接壓桿試驗,給出了屈曲荷載計算的力學模型和計算公式;Hu[3]推導了半穿式梁上弦桿的屈曲臨界力,結果表明能量法在此類復雜邊界條件桿件的屈曲計算中應用良好;Timoshenko[4]在應用能量法求解屈曲臨界力的同時,給出了上弦桿的屈曲半波數。Csagoly等[5-6]通過有限元方法證明了上弦桿軸力分布對屈曲臨界力有影響;Iwicki[7]在研究中發現彈性支撐的分布對屈曲臨界力有一定影響,但當彈性支撐數量較多時,其影響幾乎可以忽略。段明德等[8]研究發現TBJ 2—1985 《鐵路橋涵設計規范》中上弦桿臨界力按桿件等軸力計算過于保守,應按拋物線分布進行計算;程高等[9-10]基于上弦桿等軸力條件,采用能量法推導了上弦桿面外屈曲荷載的解析表達式,給出了不同節間數時屈曲荷載的簡化計算公式;孫綱廷等[11-12]將半穿式梁上弦桿簡化為橫向彈性約束的壓桿,建立了等軸力條件下的穩定方程,并通過函數逼近,給出了簡便實用的屈曲計算公式;溫慶杰等[13-15]以階梯形軸力分布和彈性支撐均布為前提,基于能量法推導了面外屈曲臨界力的理論解。另外,JTS 152—2012《水運工程鋼結構設計規范》[16]、JTJ 283—99《港口工程鋼結構設計規范》[17]和TB 10091—2017《鐵路橋梁鋼結構設計規范》[18]給出了基本相同的屈曲荷載計算方法,通過查表確定桿件計算長度系數,再考慮桿件穩定折減系數可確定屈曲荷載。

綜上可知,當前關于半穿式鋼桁梁上弦桿面外屈曲的相關研究存在下述問題:①以彈性支撐連續梁為基本模型、采用能量法推導屈曲臨界力為主要方法,但其推導過程中的假設與實際結構存在較大差別,如將上弦桿軸力簡化為等軸力,致使結果偏于保守;②分析時多將上弦桿按一定間距布置的側向支撐簡化為均布形式,與實際結構不符,且節間較少時,計算結果偏大;③推導過程中的撓曲線方程采用多項三角級數,項數越多,屈曲臨界力表達形式和計算過程越繁復,且包含多個不易確定的參數,不利于在實際工程中推廣應用。鑒于當前半穿式鋼桁梁上弦桿面外屈曲研究多限于上弦桿等軸力分布、均布彈性支撐條件、撓曲線方程復雜、計算方法實用性較差等問題,本文基于半穿式鋼桁梁屈曲模態特征,對撓曲線方程進行適當簡化,同時考慮不同的軸力分布和彈性支撐分布形式,建立4種平面計算模型,采用能量法分別推導4種模型的屈曲臨界力解析解,并與整體模型開展對比分析,探究4種模型各自特點及適用性,旨在探尋一種合理且簡單實用的屈曲臨界力計算方法,便于工程推廣應用。

1 基本模型

半穿式鋼桁梁失穩模式通常表現為面外屈曲,根據其結構特點和屈曲模態,可將空間穩定性問題轉化為平面問題,如圖1所示為半穿式梁簡化后的平面計算模型,將上弦桿視為兩端鉸接、中間設有若干彈性支撐的連續梁,圖1中L為上弦桿總長度,d為節間長度,N為節間數,k為上弦桿側向彈性支撐的剛度系數,x為半穿式梁跨長方向,y為半穿式梁上弦桿平面外屈曲方向,O為坐標原點,位于上弦桿左端。

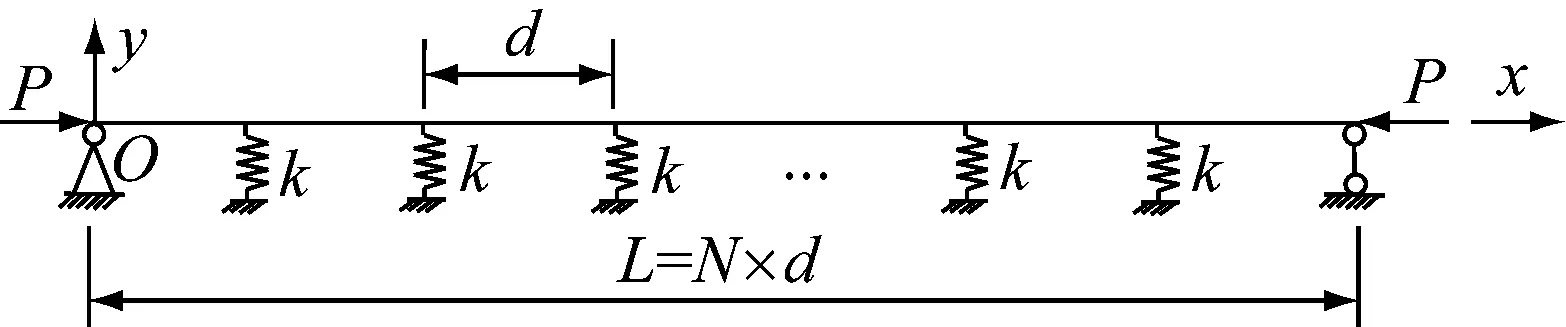
圖1 半穿式鋼桁梁簡化計算模型Fig.1 Simplified calculation model for semi-through steel truss girder

為方便計算,半穿式鋼桁梁上弦桿平面計算模型考慮以下基本假定:①上弦桿各桿件沿跨長為等截面;②上弦桿各節間距均相等;③側向彈性支撐的剛度均相同;④由于端腹桿和端支座對上弦桿橫向位移的約束作用明顯強于中間區域,故將上弦桿端部視為鉸接。

結構屈曲失穩時的撓曲線方程常采用若干項三角級數作為形函數,但這種表達形式過于復雜,不利于工程應用。本文根據不同跨徑、不同荷載作用下半穿式梁的屈曲模態特點,將撓曲線方程簡化為1項或2項三角級數。根據桿件軸力、側向支撐以及撓曲線的不同形式將平面計算模型分為4種,如表1所示。

表1 不同平面模型的基本假定Tab.1 Fundamental assumptions of different plane model

1.1 平面模型Ⅰ

本模型除滿足以上基本假定外,還需滿足以下假定:①各桿件軸力均相等,且均以桿件軸力最大值計算;②側向彈性支撐視為均勻分布的連續彈性約束;③由于結構和荷載基本對稱,則屈曲模態也為對稱形式,或正對稱或反對稱,且屈曲變形為多個半波時,其最大值相等。

此處,模型Ⅰ雖然采用了與文獻相同的等軸力假定,但由于既有文獻[11-13]中撓曲線表達式較為復雜,本文對撓曲線方程適當簡化,如式(1)所示,以便于屈曲臨界力的計算更加便捷和實用。

(1)

式中:n為屈曲模態的半波數,模態正對稱時,n為奇數,反對稱時,n為偶數;a為屈曲變形的最大值。

由式(1)求導得:

(2)

上弦桿屈曲時的彎曲應變能Ub為:

化簡得:

(3)

由于側向彈性支撐等效為均布連續彈性約束,且節間距相等,則均布彈性支撐剛度為k/d,側向支撐應變能Uk為

化簡得

(4)

外荷載P所作的功W為

化簡得

(5)

根據能量法,上弦桿總能量U為

(6)

根據能量原理,當結構處于穩定的臨界狀態時,應滿足

(7)

將式(6)代入式(7)即得

(8)

解方程式(8),可得弦桿等軸力、彈性支撐連續均布條件下,面外屈曲臨界力Pcr的計算公式為

(9)

模型Ⅰ計算理論簡單,但是側向彈性支撐等效為均布連續支撐,與實際結構相差較大,尤其是節間和側向支撐數量較少時,容易造成較大誤差。

1.2 平面模型Ⅱ

1.2.1 屈曲臨界力

本模型中側向彈性支撐按節間距等距離散布置,共有(N-1)個側向彈性支撐,其應變能Uk為

(10)

式中,xki和yki分別為第i個側向彈性支撐的位置坐標和屈曲變形值。

式(10)化簡得

(11)

由于本模型中軸力分布形式依然為等軸力,故彎曲應變能Ub、外荷載P作功W同模型Ⅰ,詳見式(3)和式(5),由此可得上弦桿總能量U為

(12)

根據能量原理,結構處于穩定臨界狀態時的平衡方程為

(13)

解方程式(13),可得弦桿等軸力、彈性支撐等間距離散布置時,面外屈曲臨界力Pcr的計算公式為

(14)

1.2.2 臨界剛度kcr

由式(14)可知,半穿式梁臨界力取決于上弦桿抗彎剛度EI、節間距d、節間數N、側向支撐剛度k以及屈曲模態半波數n,其中半波數n的取值與結構特性有關。當半穿式梁基本結構確定后,半波數n主要取決于側向支撐剛度k,當剛度k增加到一定程度,半波數則會增加1個,所以從理論上來分析,應存在臨界剛度kcr[19],此時可能出現半波數為n或(n+1)的兩種屈曲模態。由于結構基本參數相同,故在這兩種半波數不同的屈曲模態下,結構屈曲臨界力理應相同,由此即可求得臨界剛度kcr。

設半波數為n時,屈曲臨界力為Pcr1,則:

(15)

半波數為(n+1)時,屈曲臨界力為Pcr2,則:

(16)

根據相同參數下,結構屈曲臨界力相同,可得:

(17)

由式(17)可求得兩個相鄰半波數n和(n+1)之間的臨界剛度kcr,為便于區分不同相鄰半波的臨界剛度,在此將其記為kcr,n,n+1

(18)

由式(18)可確定不同相鄰半波數的臨界剛度。在確定半穿式梁屈曲臨界力時,應首先根據實際側向支撐剛度k,初判屈曲模態的半波數n,再按計算公式求解屈曲臨界力Pcr。

另外,模型Ⅰ也可基于同樣原理推導臨界剛度,但由于模型Ⅰ假定側向支撐連續分布,與實際結構有一定差別,在此不再進行詳細推導,只給出臨界剛度最終的計算公式。

(19)

1.3 平面模型Ⅲ

模型Ⅰ、Ⅱ均假定桿件軸力為等軸力分布,與實際結構相差較大。半穿式梁桿件軸力實際上呈階梯狀分布,在此設上弦桿桿件軸力最大值為P,同時引入軸力系數αi表示各桿件軸力Pi與最大軸力P之比,則有

Pi=αiP

桿件軸力不等情況下,結構屈曲模態也將發生變化,與等軸力時撓曲線有一定差異,但當假定的撓曲線與實際撓曲線半波數一致時,其計算結果誤差較小,故為簡化計算,依然可假定變形曲線為

由于變形曲線沒有變化,故彎曲應變能Ub和離散彈性支撐應變能Uk的表達式與模型Ⅱ完全相同,詳見式(3)和式(10)。

因桿件軸力實際為階梯狀變化,故外力做功需重新計算,各桿件軸力Pi做功總和W為

化簡得

(20)

將Ub、Uk和W代入能量表達式,并化簡得

(21)

根據能量原理,可得結構穩定平衡方程為

(22)

化簡并求解式(22),可得弦桿軸力不同、側向支撐等間距離散布置時,屈曲臨界力Pcr為

或表示為

(23)

式(23)即為變軸力情況下的屈曲臨界力計算公式。當弦桿軸力相同時,Pi=P,此時各桿件軸力系數αi均為1,則有:

(24)

將式(24)代入式(23),可得:

(25)

比較式(25)和式(14)可知,兩者完全相同,故等軸力模型Ⅱ可視為變軸力模型Ⅲ的一種特殊情況。由式(23)和式(25)可得變軸力屈曲荷載Pcr變和等軸力屈曲荷載Pcr等之間的關系式

(26)

在此引入軸力不等放大系數η,并令:

(27)

則式(26)可表示為

Pcr變=ηPcr等

(28)

各桿件軸力系數比αi可通過靜力分析得到,代入式(27)即可求得軸力不等放大系數η,Pcr等可按等軸力情況計算,最后通過式(28)計算變軸力情況下的屈曲臨界力Pcr變。

另外,根據結構實際側向剛度為臨界剛度時,兩種半波數不同的屈曲模態下屈曲臨界力相同,可推導出模型Ⅲ的臨界剛度kcr,其最終表達式與模型Ⅱ的式(18)完全相同,故可根據式(18)確定模型Ⅲ的半波數n。

1.4 平面模型Ⅳ

模型Ⅲ撓曲線方程設為一項三角級數,與變軸力情況下結構失穩曲線有一定偏差,為獲得更準確的結果,可將撓曲線方程設為

則:

(29)

上弦桿彎曲應變能Ub為

化簡得

(30)

側向彈性支撐應變能Uk為

化簡得

(31)

各桿件軸力Pi做功總和W為

化簡得

(32)

其中,

(33)

上弦桿總能量U為

U=Ub+Uk-W

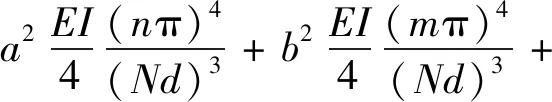
(34)

根據能量原理,當結構處于穩定的臨界狀態時,應有

即:

化簡得:

(35)

式(35)為一元二次方程,其較小解即為屈曲臨界力,鑒于屈曲臨界力與半波數取值有關,故欲求屈曲荷載,需首先確定半波數n和m取值。由于模型Ⅳ屈曲荷載計算過程繁復,不宜進行臨界剛度的推導和計算,建議參考模型Ⅱ中式(18)計算臨界剛度,并估算半波數n。當實際剛度和臨界剛度相近時,可適當調整半波數以獲得更準確的屈曲半波數。根據屈曲模態的對稱性和三角函數特點,m可取為(n+2)或(n-2)。根據不同的n和m值,所求得的臨界力會有所不同,其最小者即為屈曲臨界力。

另可證明,若m取為0,則所得結果與模型Ⅲ相同,故模型Ⅲ可視為模型Ⅳ的特例。同時可通過對比模型Ⅲ、Ⅳ計算結果的差異,判斷所假定的撓曲方程是否合適,如果計算結果仍然不能滿足精度要求,可采用三項三角級數進行求解,或參考相關文獻[13]進行修正。

2 驗證與分析

上述4種平面計算模型,由于結構簡化程度和撓曲線方程不同,故計算結果準確度也隨之不同,且都存在不同程度的誤差。下面以半穿式鐵路應急鋼桁梁為例,采用不同模型計算上弦桿屈曲臨界力,并以整體模型計算結果為基準,通過對不同模型計算結果的對比分析,確定屈曲臨界力計算的優選方法,以便在半穿式鐵路應急鋼桁梁設計中推廣應用。

2.1 工程概況

鐵路應急鋼桁梁主桁采用無豎桿的三角形結構體系,主桁桿件有標準桿件和畸零桿件兩種,可根據需要拼組不同跨徑鋼桁梁。中小跨徑鋼桁梁通常采用半穿式結構,主桁高h為6 m,主桁寬B為6.5 m,標準節間距d為6 m,輔以4 m節間距進行跨徑調整,可拼組24 m、32 m、40 m、48 m、56 m和64 m等不同標準跨徑的半穿式鐵路應急鋼桁梁,主桁弦桿均采用相同尺寸的雙槽鋼截面。圖2為56 m跨鐵路應急鋼桁梁結構圖,其他跨徑半穿式梁的結構形式與之相同。

(a) 正面

2.2 整體結構的仿真分析

為全面考慮半穿式梁結構的整體效應,本文借助于有限元軟件ANSYS建立不同跨徑半穿式梁的三維整體模型,通過線彈性穩定分析[20],確定結構的屈曲模態和失穩荷載。圖3所示為應急鋼桁梁設計活載,為便于統一荷載工況,整體結構計算中僅考慮恒載和活載中隨掛均布荷載進行組合,主桁、聯結系和橋面系各桿件均采用3維鐵摩辛柯梁單元beam189模擬[21],圖4所示為56 m半穿式應急鋼桁梁的有限元模型。

圖3 半穿式應急鋼桁梁設計活載Fig.3 Design live load of 56 m semi-through emergency steel truss girder

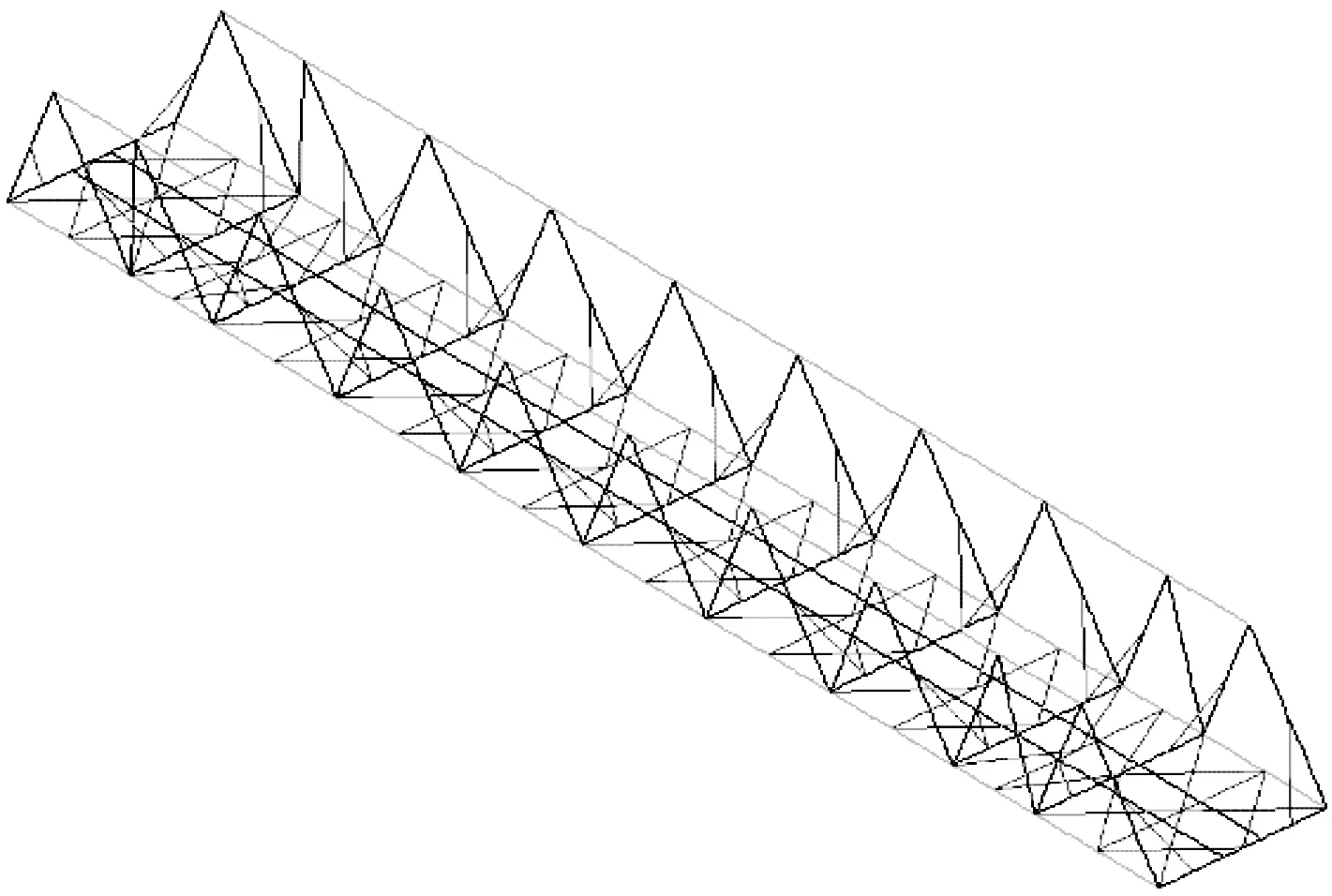
圖4 56 m半穿式應急鋼桁梁有限元模型Fig.4 Finite element model of 56 m semi-through emergency steel truss girder

圖5為不同跨徑半穿式梁的屈曲模態,由圖5可知,不同跨徑的半穿式梁,其失穩模式也不同,其中24 m半穿式梁表現為局部失穩,端部腹桿和風撐首先破壞,其他跨徑半穿式梁均表現為上弦桿的面外失穩,屈曲模態半波數隨跨徑增加由1逐漸增加到3,表明在側向支撐剛度相同條件下,屈曲半波數隨節間數增加而有所變化。

(a) 24 m

表2為不同跨徑半穿式梁屈曲分析的計算結果,表中屈曲臨界力為失穩破壞時,上弦桿軸力最大值。由表2可知,不同跨徑的線彈性穩定系數差別較大,隨著跨徑增大,穩定系數逐漸減小,但屈曲臨界力除24 m跨外其他跨徑差別不大,主要原因是荷載作用下,上弦桿跨中桿件受力最大,是半穿梁整體失穩的控制桿件,由于不同跨徑弦桿截面尺寸和側向支撐剛度相同,故結構處于失穩臨界狀態時,跨中桿件軸力均達到相同的臨界值。另外,24 m半穿式梁因端部桿件局部失穩而破壞,原因是相比其他跨徑半穿式梁,24 m跨徑相對較小,故相同荷載引起的上弦桿軸力隨之減小,穩定性相對提高。同時由于半穿式梁腹桿截面尺寸比弦桿尺寸小,因此腹桿通常先于弦桿而破壞,但由于穩定系數接近50,遠高于結構作用荷載,故實際工程中,24 m跨徑半穿式梁結構穩定性有足夠高的安全保障,局部失穩不會發生。

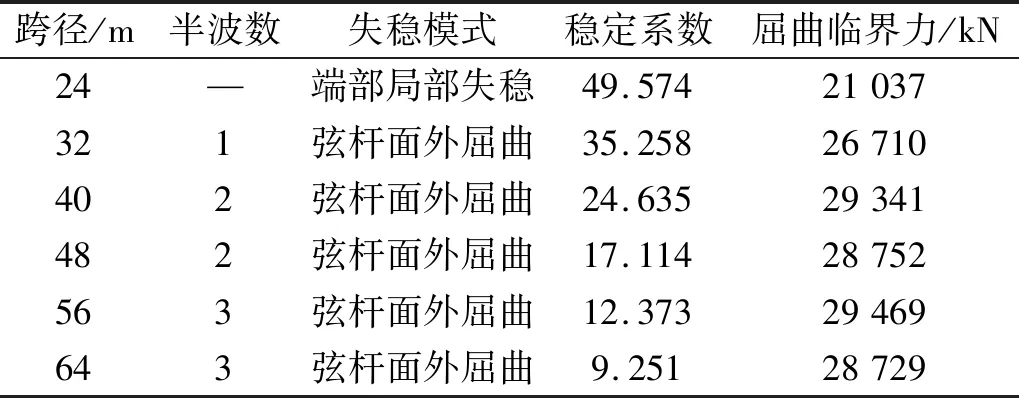
表2 不同跨徑半穿式梁整體模型計算結果Tab.2 Calculation result of semi-through girder with different span

圖6為不同跨徑半穿式梁上弦桿軸力系數分布圖,由圖6可知,不同跨徑的軸力分布形式大致相同,均呈拋物線規律變化,跨中桿件軸力最大,向兩端逐漸減小。但是跨徑越大,軸力分布越不均勻,鋼桁梁設計時中可根據軸力分布規律選擇不同的截面尺寸。

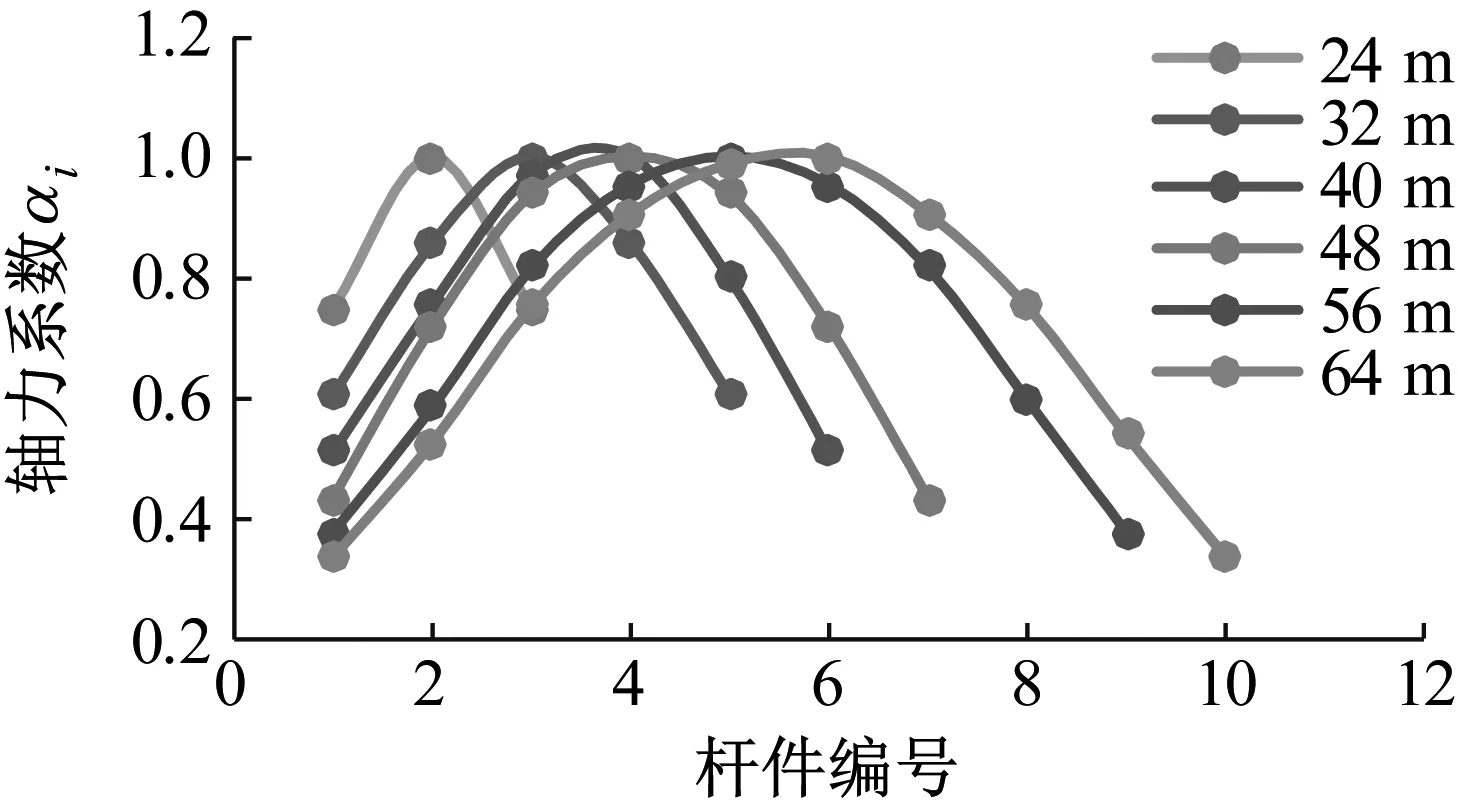
圖6 不同跨徑半穿式梁上弦桿軸力系數分布圖Fig.6 Axial force coefficient of upper chord of semi-through girder with different span

2.3 基于平面模型的理論計算

2.3.1 計算側向支撐剛度k

平面模型中側向支撐剛度k由半框架提供,不同跨徑鐵路應急鋼桁梁采用相同的半框架結構,同時為增強半穿式梁橫向穩定性,在腹桿和橫梁間加裝了風撐,如圖7所示。由于風撐對半框架受力影響顯著,故在半框架受力分析中應考慮風撐的影響,可參考相關文獻[12]進行計算。經計算,本文所示半框架在1 N單位水平荷載作用下的側向位移為0.362×10-6m,上弦桿側向彈性支撐剛度k為2.759×106N/m。

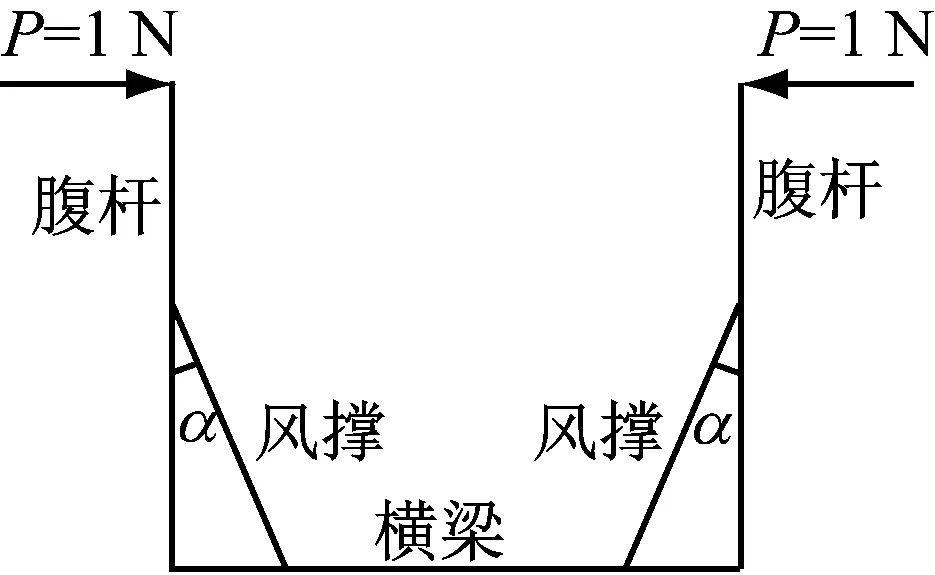
圖7 半穿式鋼桁梁半框架圖示Fig.7 Semi-frame graphics of semi-through girder

2.3.2 計算半波數n

半穿式梁屈曲半波數的確定有2種方法:臨界剛度法和根據規范查表法,在此主要介紹臨界剛度法。首先,根據式(18)計算不同跨徑半穿式梁不同相鄰半波間的臨界剛度kcr,然后將實際支撐剛度k與臨界剛度kcr進行比較,即可確定半穿式梁屈曲半波數n。

根據規范和工程經驗可知,半穿式鋼桁梁屈曲半波數一般在1～5,故只需計算1和2、2和3、3和4、4和5四種相鄰半波數的臨界剛度,計算結果如表3所示。由表3可知,同一跨徑的半穿式梁臨界剛度隨半波數增加而增加,不同跨徑半穿式梁臨界剛度隨跨徑逐漸減小。

表3 不同跨徑半穿式梁的臨界剛度與半波數Tab.3 Critical stiffness and half-wave of semi-through girder with different span

本文半框架提供的側向支撐剛度k為2.759×106N/m,與臨界剛度kcr進行對比,即可確定不同跨徑半穿式梁的失穩模態半波數n,如表3所示。由表3可知,平面模型半波數可能與整體模型分析半波數有差別,原因是平面模型以經典歐拉梁理論為基礎[22-23],沒有考慮剪切對結構穩定性的影響,在一定程度上高估了結構的整體剛度,且平面模型是對整體結構的簡化,很難全面考慮結構的空間效應;整體模型中采用的是鐵摩辛柯梁理論,考慮了截面剪切、扭轉變形對穩定性的影響,因此當實際支撐剛度k與臨界剛度kcr相接近時,平面模型半波數與整體模型會有所不同,且平面模型半波數較大。

2.3.3 計算屈曲臨界力Pcr

根據前面的側向支撐剛度k和屈曲半波數n,分別代入4種平面模型計算公式,即可求得不同跨徑半穿式梁的屈曲臨界力Pcr,如表4所示。

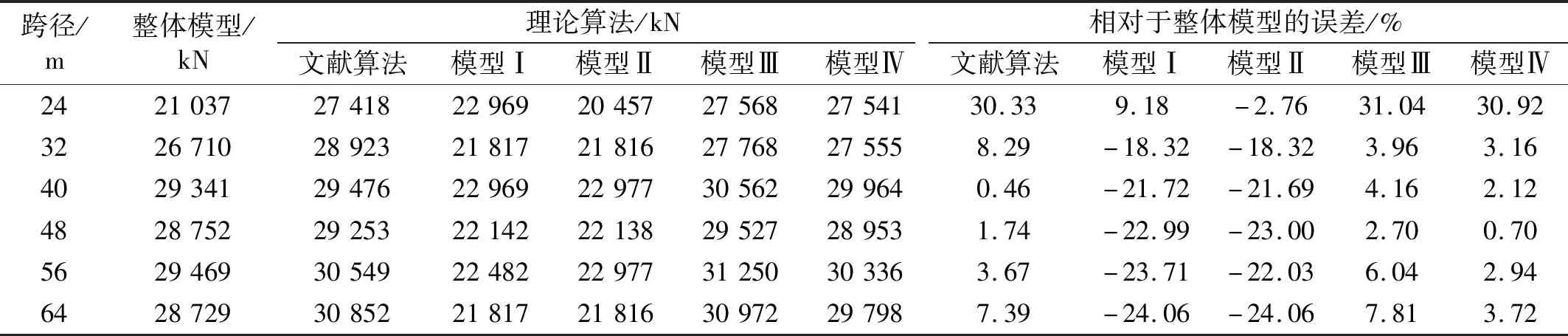
表4 不同模型屈曲臨界力計算結果比較Tab.4 Comparison of calculation results of different models

由表4可知,模型Ⅰ、Ⅱ計算結果基本相同,由于兩種模型均沒有考慮軸力不等的影響,認為各桿件軸力與上弦桿最大軸力相同,故計算結果明顯低于整體模型,誤差為18%～24%,雖偏于安全,卻過于保守,不宜直接作為屈曲臨界力的計算方法;模型Ⅲ、Ⅳ計算結果相近,兩種模型均考慮了上弦桿軸力分布不均勻的影響,故計算結果與整體模型相差不大,最大誤差約7.81%,明顯低于等軸力模型,因此屈曲臨界力計算應優先考慮這兩種方法。另外模型Ⅰ、Ⅱ與模型Ⅲ、Ⅳ結果差異明顯,也表明了軸力分布形式對結構屈曲臨界力影響很大,穩定分析中應考慮桿件軸力的實際分布特點,不能簡單的按等軸力處理。

模型Ⅲ、Ⅳ計算結果雖然相近,但相比之下,模型Ⅳ誤差更小,最大誤差只有3%,與整體模型結果更接近,計算結果更準確,其原因在于兩種模型采用的撓曲線方程不同,模型Ⅲ采用1項三角級數,模型Ⅳ采用2項三角級數,模型Ⅳ與整體結構屈曲變形曲線更接近,因此就準確度而言,模型Ⅳ最優,不僅考慮了軸力不等、彈性支撐的離散性,且撓曲線方程與實際屈曲變形的吻合度更高,故計算結果更準確。不足之處是計算公式繁復,在工程實用性方面略遜一籌。模型Ⅲ計算結果雖然相比模型Ⅳ誤差略大,但依然可滿足工程計算精度要求,也可作為屈曲臨界力計算的優選方法。而且該法計算公式簡單,可通過對等軸力情況下臨界力Pcr等進行修正得到準確度較高的結果,因此綜合考慮計算準確性和工程實用性,建議采用模型Ⅲ的計算公式作為半穿式梁屈曲臨界力的簡化計算方法。

為了進一步驗證本文算法的準確性和實用性,本文采用文獻[13]的方法計算了不同跨徑半穿式梁的屈曲臨界力,見表4。通過計算結果的對比可知,模型Ⅲ與文獻算法的結果非常接近,最大誤差只有4.33%。鑒于兩種方法均考慮了軸力不等的影響,但文獻算法中由于變形曲線假設為多項三角級數,使屈曲臨界力計算非常繁復,實用性較差,相比之下本文模型Ⅲ的計算方法更簡潔。

另外,24 m半穿式梁理論計算結果有些異常,原因是整體模型中24 m半穿梁失穩是由端部桿件破壞引起,而平面模型是按整體失穩考慮的,因此整體模型和平面模型計算的前提條件不同,故計算結果差異很大,兩種結果的對比也沒有意義。除此之外,還注意到24 m跨的模型Ⅰ和模型Ⅱ計算結果差別很大,原因是24 m跨半穿式梁上弦桿只有3個節間,2個側向支撐,將離散的側向支撐等效為連續均布形式與實際結構相差太大,因而計算結果不準確,建議中間支撐數<4,即節間數N<5時,側向支撐按離散布置考慮。

綜上所述,不同跨徑半穿式梁不同算法的計算結果對比表明,基于變軸力條件的模型Ⅲ計算方法既準確又實用。本文的簡化算法有助于工程設計人員快速而準確地選取半穿式梁桿件截面,為后續數值模擬提供便捷,因此本文算法對半穿式應急鋼桁梁的設計有重要意義。

3 結 論

本文將半穿式鋼桁梁上弦桿簡化為側向彈性支撐下的連續梁,采用能量法推導了4種不同平面計算模型的屈曲臨界力解析解,通過與不同跨徑半穿式鋼桁梁整體模型和文獻算法計算結果的對比,探討了各平面模型的優缺點及其適用性,最后給出了便于工程應用的優選方法,主要結論如下:

(1) 建立了等軸力與不等軸力、均布連續與均布離散彈性支撐以及不同撓曲線方程下的穩定方程,給出了不同情況下屈曲臨界力的解析解。

(2) 以等軸力、離散彈性支撐條件下的模型為基礎,推導了相鄰半波數之間的臨界剛度計算公式,給出了屈曲半波數的確定方法。

(3) 建立了不同跨徑半穿式鋼桁梁的整體模型,分析了不同跨徑半穿式梁的線彈性穩定系數、屈曲模態和失穩軸力,結果表明:隨著跨徑增大,線彈性穩定系數逐漸減小,屈曲模態半波數有所增加,但失穩時上弦桿最大軸力基本保持不變。

(4) 相比整體模型和文獻算法,基于等軸力條件的模型Ⅰ、Ⅱ計算結果明顯偏小,過于保守,不宜直接采用;基于變軸力條件的模型Ⅲ、Ⅳ計算結果與整體模型相接近,計算精度均可滿足工程需要,但模型Ⅳ計算過程繁復,而模型Ⅲ計算簡單,可通過對等軸力計算值的修正獲得準確度較高的結果。綜合考慮準確性和實用性,建議采用模型Ⅲ作為屈曲臨界力計算的首選方法。