鋼絲繩隔振器的數學建模與參數識別

王冬雪，孟憲松，閆 明，孔祥希

（沈陽工業大學機械工程學院，遼寧 沈陽 110870）

1 引言

鋼絲繩隔振器是由美國在70年代末研制出的一種非線性隔振器［1］，與其它隔振器相比具有良好的干摩擦阻尼特性及遲滯特性，可以吸收振動過程中的大部分能量，同時還兼顧了彈性元件的隔振、緩沖、降低高頻結構噪聲等三大功能，被廣泛應用于航空航天、化工設備控制、各種機械、建筑物等各個領域的防沖隔振中［2-4］。

不同于普通的隔振器，鋼絲繩隔振器的剛度和阻尼均呈現出了非線性的特征，具體表現在結構非線性、材料非線性及幾何非線性等方面［5-6］，而鋼絲繩隔振器內部的結構阻尼［7］使得鋼絲繩隔振器在加載和卸載的過程中產生了遲滯回線，從而出現了明顯的遲滯特性［8-9］，而分析該遲滯特性需要引入相應的遲滯模型。所以目前關于鋼絲繩隔振器的非線性遲滯模型的研究一直是重中之重。

目前常用的非線性遲滯模型有雙線性模型、跡法模型、多項式模型和Bouc-Wen模型等［10］。當前應用最廣泛、識別精度最高的是Bouc-Wen模型。Bouc-Wen 模型是由Bouc［11］于20世紀70年代提出的一種描述遲滯回線的模型，該模型是通過將純遲滯恢復力和變形與模型參數聯系在一起，最終通過合理的選擇模型參數，來描述各種各樣的動力學系統，從而對工程中遇到的各種非線性現象來進行相應的模擬［12-13］但由于Bouc-Wen 模型在識別鋼絲繩隔振器上仍存在識別困難及一些局限性的問題［14］。所以出現了很多基于Bouc-Wen模型改進的遲滯模型，以此來更好的描述鋼絲繩隔振器的遲滯特性。

從遲滯模型出發，以分解識別方法［15］為基礎，對鋼絲繩隔振器的遲滯模型的參數識別進行了分析。首先通過對鋼絲繩隔振器進行靜態試驗得到了鋼絲繩隔振器的遲滯回線，然后詳細介紹了識別過程，針對牛頓迭代法識別結果不收斂、迭代周期長的特點，利用遺傳算法識別出遲滯模型的各項參數，再用Matlab畫出遲滯模型下的鋼絲繩隔振器的理論遲滯回線，將其與試驗遲滯回線進行對比，來驗證該識別方法的有效性及參數識別結果的正確性。

2 試驗研究與參數識別

通過對鋼絲繩隔振器進行準靜態試驗，可以獲得鋼絲繩隔振器的遲滯回線，進而可以得到鋼絲繩隔振器在加載和卸載時的力和位移的試驗數據，通過將試驗數據代入遲滯模型中，利用遺傳算法可以準確的識別出遲滯模型中的相關參數。

2.1 試驗研究

T型鋼絲繩隔振器也稱為條形鋼絲繩隔振器，是應用最早也是最廣的一種鋼絲繩隔振器，具體結構，如圖1所示。

圖1 T型鋼絲繩隔振器Fig.1 T-Wire Rope Vibration Isolator

首先將鋼絲繩隔振器通過上下兩個夾具及螺栓安裝固定在萬能材料試驗機上，然后對鋼絲繩隔振器施加位移載荷，如圖2所示。通過操作計算機和試驗機對鋼絲繩隔振器進行壓縮和拉伸，壓縮和拉伸位移為20mm，試驗機內部的位移傳感器和力傳感器會將位移數據和力的數據傳送到計算機上，計算機會根據位移和力的數據繪制出鋼絲繩隔振器的遲滯回線，如圖3所示。

圖2 鋼絲繩隔振器拉壓方向試驗測量裝置Fig.2 Measuring Device for Tension and Compression Direction of Wire Rope Vibration Isolator

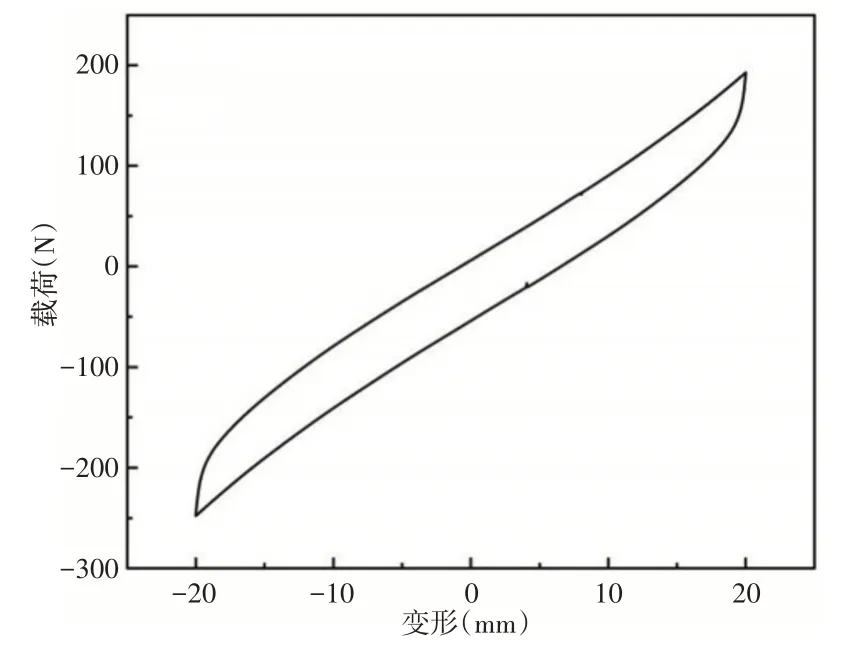
圖3 鋼絲繩隔振器拉壓方向的遲滯回線Fig.3 Hysteresis Loop in Tension and Compression Direction of Wire Rope Vibration Isolator

2.2 參數識別

首先將遲滯模型改寫為只與變形和載荷有關的函數［15］，如下式所示：

式中：x—變形；F—隔振器載荷；sgn—符號函數；z—總恢復力，式（4）為Bouc-Wen遲滯模型，式（2）和式（3）是結構調整項，待識別的參數為：h、k1、k2、k3、b、α、β、γ、n。

非Bouc-Wen模型參數的識別比較簡單，而且文獻［15］中介紹的很詳細，在這里簡單介紹一下識別流程，便不再贅述。首先常數項h的識別即是調整中心對稱點，將變形為零時的上下載荷相加除以2即可得到h=30.06N；然后根據式（5）并利用最小二乘法可識別出三次擬合項系數k1、k2、k3的值分別為8.2183、-0.0179、0.0034。

最后將遲滯曲線兩個端點的坐標（X1，-max，F1，-max）、（X1，+max，F1，+max）帶入式（1）并相除即可得出b的表達式，如式（6）所示。

通過代入試驗數據，可以得出b=1.0006。

以上5個參數識別起來較為簡單，且不存在什么大的問題，但在嘗試用原方法識別α、β、γ、n時卻出現了識別結果不收斂，計算周期長等特點，所以這里采用適用于求解非線性問題的遺傳算法來進行識別，識別過程如下（其中α、β、γ、n的取值范圍依次為：（（-300，300）、（-5，5）、（-5，5）、（0，1））

誤差函數為：

其中：

首先將式（8）的微分方程根據遲滯回線分為以下3段，如圖4所示。

圖4 分段遲滯回線Fig.4 Segmented Hysteresis Loop

以變形為0時為界限，將鋼絲繩隔振器的遲滯回線分為以下三段：（1）（0～20）mm、（2）（20～（-20））mm、（3）（（-20）～0）mm；易知第1、3段曲線dx＞0故式（8）可改寫為：

同理第2段曲線dx＜0時，則式（8）可改寫為：

然后利用ode45對微分方程進行解算，并將解算結果與F3（x）做差便可得到誤差函數。而對應的非線性最小二乘式為：

通過計算最小二乘式及利用遺傳算法進行搜索得到的誤差最小的一組參數識別結果如下：α、β、γ、n=11.7767、2.6024、2.4416、0.2230。

至此，所有參數的識別結果，如表1所示。

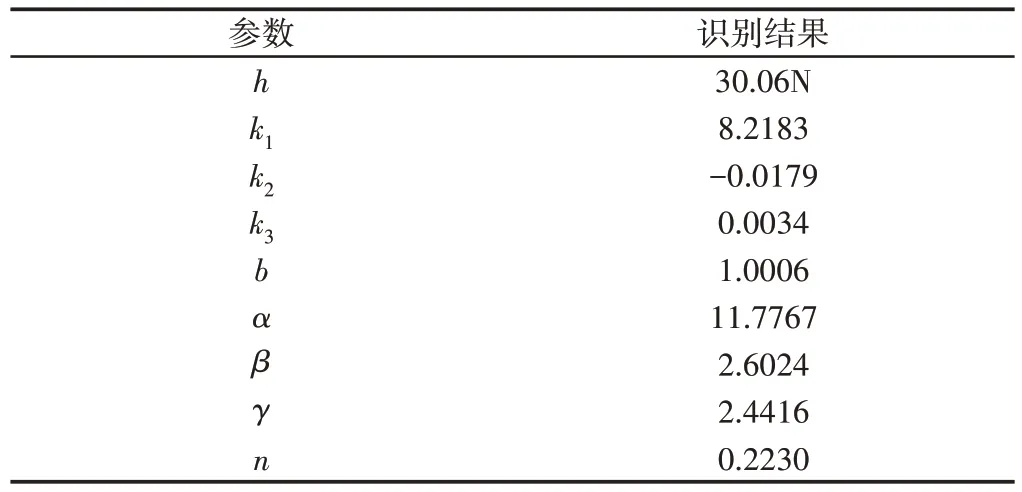
表1 遲滯模型參數識別結果Tab.1 Parameter Identification Results of Hysteresis Model

3 結果及驗證

根據上述識別結果，可得到鋼絲繩隔振器的數學模型如下：

根據上述數學模型，用Matlab 畫出該模型下的理論遲滯回線，為了驗證參數識別結果及該數學模型的正確性，將鋼絲繩隔振器的理論遲滯回線與試驗遲滯回線的對比圖表示，如圖5 所示。并根據相對誤差計算式（17）可計算出該模型下理論遲滯曲線與試驗遲滯曲線的相對誤差δ為6.23%左右，其中y為試驗得到的載荷數據值。由圖5可知，理論模型得到的遲滯回線與試驗測得的遲滯回線趨勢相同，基本吻合，從而驗證了識別過程和數學建模的正確性，進而也驗證了遺傳算法對于解決鋼絲繩隔振器參數識別的有效性。

圖5 試驗遲滯回線與理論模型曲線對比圖Fig.5 Comparison of Experimental Hysteresis Loop and Theoretical Model Curve

4 結論

通過理論分析、數值仿真及試驗驗證等步驟，對于提出的識別鋼絲繩隔振器遲滯模型的方法—遺傳算法識別法進行了驗證，結論如下：

遺傳算法識別法可準確有效的識別出T型鋼絲繩隔振器的遲滯模型參數，且由于識別過程中運用了最小二乘法尋優及通過不斷改變遺傳算法的變異系數和交叉頻率來進一步對參數進行尋優的雙重尋優方法，大大減小了識別參數的誤差，提高并保證了識別結果的準確性；遺傳算法識別出的鋼絲繩隔振器的理論遲滯曲線與試驗遲滯回線比較吻合，能夠有效的反映出鋼絲繩隔振器的遲滯特性，且通過計算可知相對誤差較小為6.23%。綜上，該方法能夠有效的識別出鋼絲繩隔振器的遲滯模型參數，為之后鋼絲繩隔振器的數學建模和參數識別研究提供了新的思路，也為鋼絲繩隔振器的動力學性能分析奠定了一定的基礎。