陳高勇，何 彬，趙 剛

（1.武漢科技大學機械自動化學院，湖北 武漢 430081；2.湖北理工學院機電工程學院，湖北 黃石 435000）

1 引言

結構優化可分為尺寸優化、形狀優化和拓撲優化，其中拓撲優化是一種根據給定的負載情況、約束條件和性能指標，在給定的區域內對材料分布進行優化的數學方法［1］，由于設計出的結構性能更好，被學者們及工程人員大量研究和使用，以增加結構強度、改變結構固有頻率或減少結構重量［2-6］。拓撲優化技術設計出的結構通常較復雜，導致了結構加工困難。為了降低拓撲結構的加工難度，文獻［7］將汽車保險杠橫截面拓撲結構中的孔洞用長方形孔洞替代；文獻［8］將汽車轉向垂臂的拓撲結構中孔洞改成長方形和圓形孔洞；文獻［9］在設計火箭外殼的掛飛結構時，以長方形為設計基礎在結構上添加孔洞。目前學者們普遍依據拓撲結構進行二次設計，將結構中不利于加工的孔洞進行形狀及參數的調整，然而在設計時都選擇與拓撲結構中孔洞形似的規則圖形作為設計基礎，當結構中孔洞極不規則時，這種選擇方法就不一定是最優解。這里提出一個客觀的評價方法，以結構的性能改變最小為優化目標，尋求對拓撲結構中孔洞規則化的最優解。

2 結構拓撲優化

這里提出的是基于拓撲結構的設計方法，需要一結構作為設計的基礎。此處選取一案例進行分析，如圖1 所示。此結構的長L、寬W、厚T分別為90mm、45mm、1mm；材料彈性模量E=200GPa；泊松比系數v=0.3；材料用量f=40%。結構左端固定，垂直向下的力F1=200N 均勻作用在右側面上方（4×1）mm，垂直向下的力F2=100N 均勻作用在底面正中間區域（4×1）mm，不考慮材料自重。

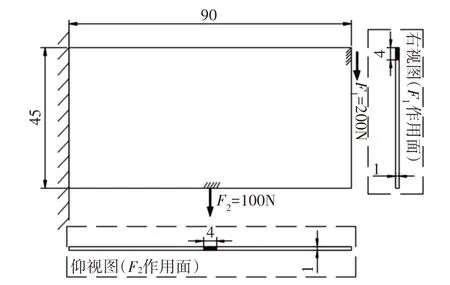
圖1 材料尺寸及邊界條件Fig.1 Material Size and Boundary Conditions

采用O.Sigmund 編寫的MATLAB 程序［10］將圖1 進行拓撲結構優化處理。將該結構劃分為（90×45）個單元，由于程序中的彈性模量E取值過大會影響單元密度值xi的迭代速度，設程序中彈性模量E=1000Pa（程序中彈性模量E的改變不影響最終優化結果），可得出拓撲優化結構，為了使結構清晰，將結構中的少量中間密度單元的xi進行修改：當xi＞0.2時，令xi=1；當xi＜=0.2時，令xi=0.001。得出結果，如圖2所示（由于該圖形是由（90×45）個單元組成，因此會有鋸齒邊界現象）。此時拓撲結構體積V=1755mm3。

圖2 MATLAB程序拓撲優化結構圖形Fig.2 Topology Optimization Structure Graphic in MATLAB Program

3 結構二次設計

3.1 結構二次設計原理

拓撲優化完成后，需對拓撲優化圖形進行二次設計。將圖形中白色部分看作為孔洞。選取四種形狀作為設計基礎，用于替換拓撲結構中的孔洞，如圖3所示。每個圖形都有對應的變量a和b用于描述圖形的大小，如表1所示。

表1 變量a，b在圖形中的含義Tab.1 The Meaning of a and b in Graphics

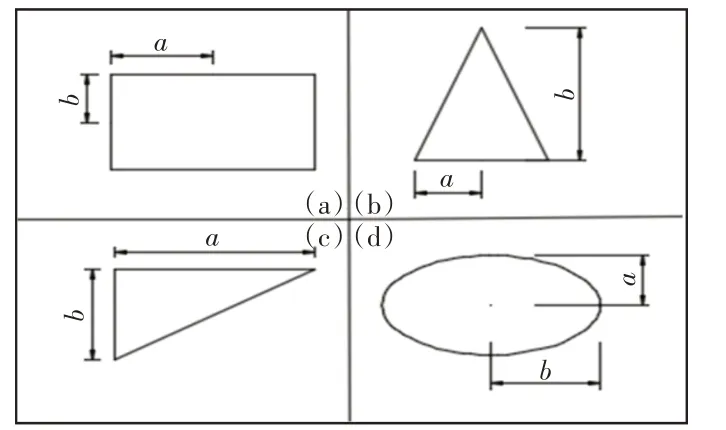
圖3 基本設計圖形Fig.3 Basic Graphics Used to Design

設β為所有圖形圍繞該圖形形心順時針旋轉的角度，將以上四個圖形（a），（b），（c），（d）依次編號為1～4。以柔順度比例系數c作為優化目標，圖形編號n、尺寸a，b以及旋轉角β為自變量，當需對某一不規則孔洞進行替換時，可以建立優化模型：

式中：C和V1—規則孔洞替代不規則孔洞后的結構柔順度及體積；V0—初始材料體積；F和U—當前工況下的結構力場及結構位移場；xi—第i號單元的密度值；p—懲罰因子；Ui—第i號單元的位移矢量；Ki—xi=1時單元剛度矩陣；V—初始拓撲結構體積；Vmax—需被替換的不規則孔洞的體積；V2—規則圖形產生孔洞的體積；k—等比縮小系數；Vmin—設定規則孔洞體積的最小值。優化過程流程圖，如圖4所示。

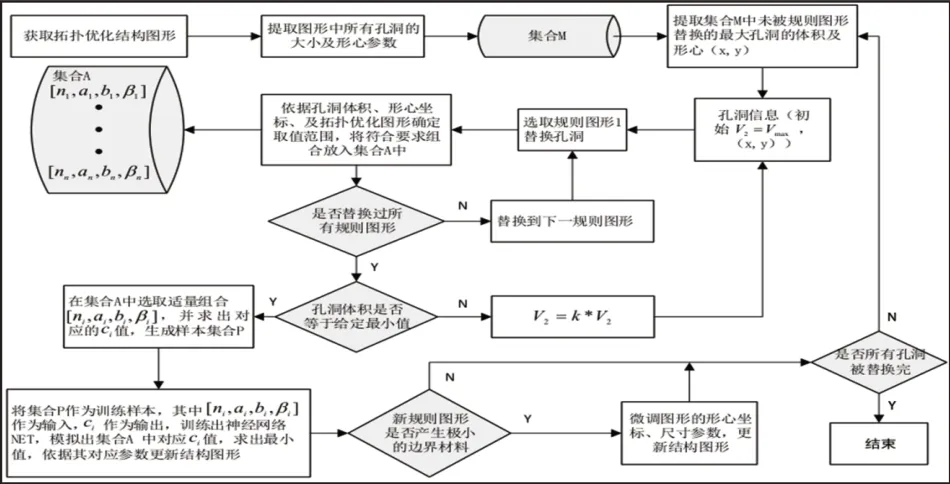
圖4 二次設計流程圖Fig.4 Secondary Design Flow Chart

3.2 結構二次優化步驟

以圖2為例，懲罰因子p=3時，用式（2）可計算出此時結構柔順度C=4106.2。用MATLAB編程計算出拓撲優化圖形孔洞的大小及形心坐標數據，并按照孔洞體積大小進行編號。編號及坐標軸，如圖5所示。并得出數據，如表2所示。

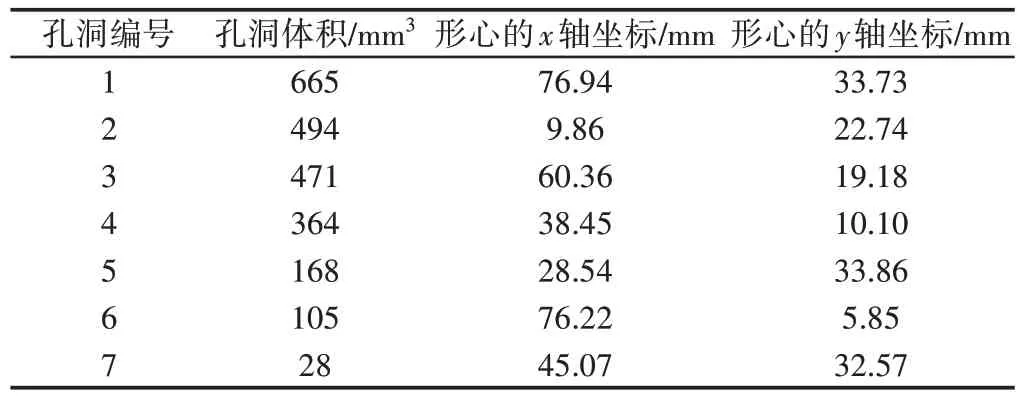
表2 拓撲優化圖形孔洞參數Tab.2 Hole Parameters in Topology Optimization Graphic

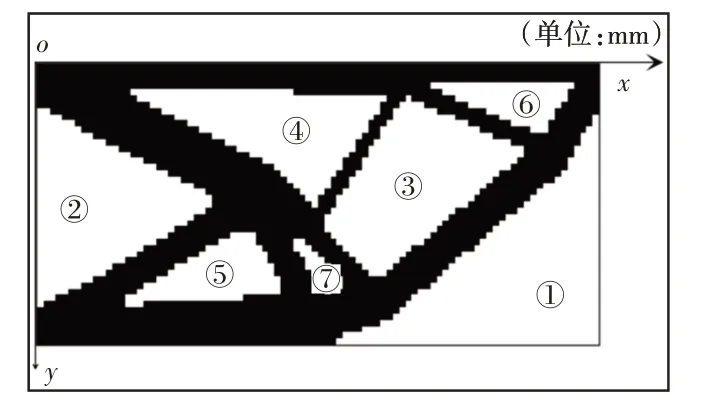
圖5 結構圖形中孔洞編號Fig.5 Hole Number in Structural Graphic

當被替換的孔洞的體積Vmax、孔洞對應的形心坐標（x，y）、等比縮小系數k、孔洞最小體積Vmin確定后，用公式可確定孔洞參數n，a，b，β的取值范圍，為了使n，a，b，β參數產生的圖形孔洞對原孔洞有較好的代替效果，需對規則圖形孔洞進行限制。令規則圖形孔洞滿足條件：（1）替換后的規則圖形孔洞在原材料范圍內（可能在邊界處產生尺寸極小的邊界材料，后續通過調整孔洞參數及形心坐標消除）；（2）替換后規則圖形孔洞不與其他孔洞接觸。為了保證n，a，b，β的精度并且n，a，b，β參數取不同值時所對應的c值有較大的變化，從而使后續神經網絡有較好的擬合效果，令a，b單次變化最小值為0.5mm，β單次變化最小值為3o。遵循以上規則就能求出所有n，a，b，β參數組合。例如，比例系數k=0.95、Vmin=k7×Vmax時，對3號孔洞進行替換時，共有929組符合條件的參數組合。n，a，b，β取值為［1，8.5，10.5，42］時對應的優化結構圖形，如圖6所示。孔洞替換的過程為：①將需要替換的孔洞內的全部單元的xi值改為1；②依據n，a，b，β組合的值及原孔洞的形心坐標構建出規則圖形；③將中心點在規則圖形內的所有單元的xi值改為0.001。因此，程序上進行二次優化的圖形依舊會有鋸齒邊界現象。但在ANSYS上依據n，a，b，β參數組合進行建模時則不會出現此現象。

圖6 3號孔洞替換后的結構圖形Fig.6 Structure Graphic After Hole 3 is Replaced

當結構圖形確定后，可得出結構的整體體積V1以及全部單元的密度值xi（黑色部分xi=1，白色部分xi=0.001），結合初始的材料條件、邊界條件，根據式（2）可求出該結構的柔順度C，再結合式（1）可求出柔順度比例系數c。經計算圖6結構的c=1906.2。

3.3 神經網絡求解

計算全部n，a，b，β參數組合對應的c值需要很大的計算量，為了簡化計算，采用BP 神經網絡算法對c值進行擬合。以n，a，b，β參數組合作為輸入，其對應柔順度比例系數c為輸出。取n，a，b，β參數組合及對應c值的總數量的10%為訓練樣本，如表3所示。另選取10組參數組合為測試樣本，設神經網絡隱層第一層節點數為20；隱層第二層節點數為40；訓練次數為1000；訓練精度為1e-5。擬合效果，如圖7所示。根據測試樣本（表4）可看出預測c值與實際c值十分接近。訓練的神經網絡可精確模擬出全部n，a，b，β參數組合的c值，并求出當n，a，b，β為［4，14.0，9.5，45］時，c為最小值1871.6，對應的結構圖形，如圖8所示。

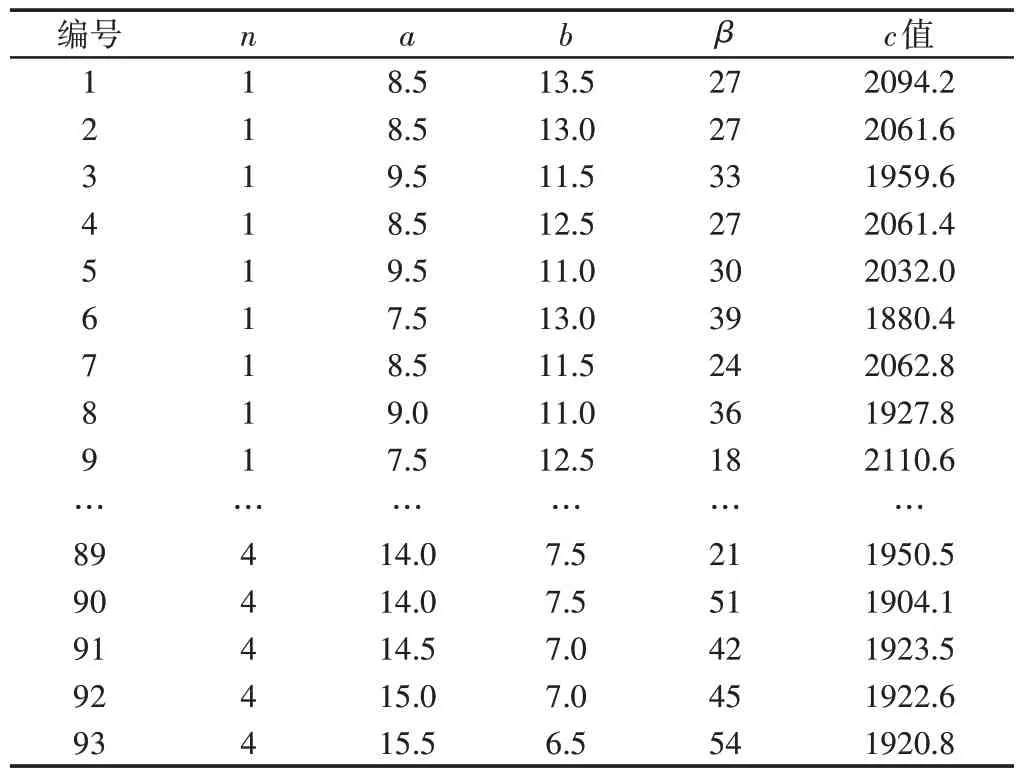
表3 神經網絡訓練樣本Tab.3 Neural Network Training Samples

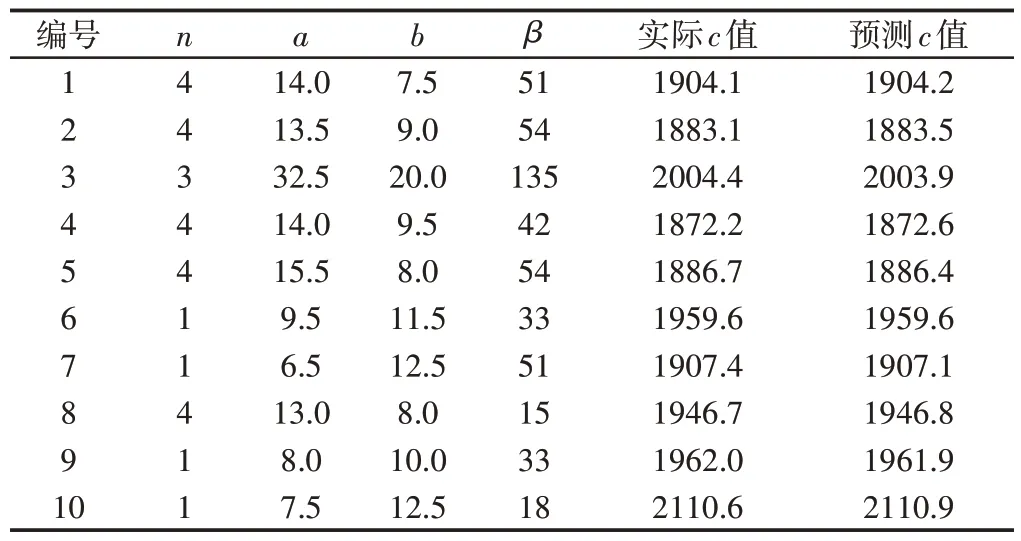
表4 神經網絡測試據Tab.4 Neural Network Test Data

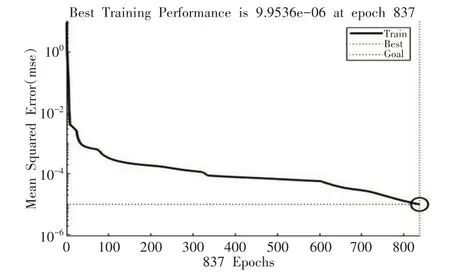
圖7 神經網絡擬合圖Fig.7 Neural Network Simulation Diagram

圖8 3號孔洞替換后的最終結構圖形Fig.8 Final Structure Graphic After Hole 3 is Replaced

依次對圖形中1～7號孔洞依次進行替換，最終優化圖形，如圖9所示。并得出以下孔洞參數，如表5所示。此時結構體積V=1943mm3，相對初始拓撲結構增加10.71%，結構柔順度C=3903.3，同比減少5%。

表5 二次設計后孔洞參數Tab.5 Hole Parameters After Secondary Design

圖9 最終設計結構圖形Fig.9 Final Structure Graphic After Secondary Design

4 結構分析

為了驗證了該方法的可行性和有效性，依照表5中數據將結構在ANSYS軟件中重建，同時將圖2結構重建作為參照物，二者的材料系數及受力條件與初始材料（圖1）保持一致，將結構進行應力分析后得出結果，如圖10、圖11所示。比較得出二次設計后的結構應力圖與初始拓撲結構應力圖相似，并未出現由結構改變而引起的應力集中現象，驗證了結構的實用性。

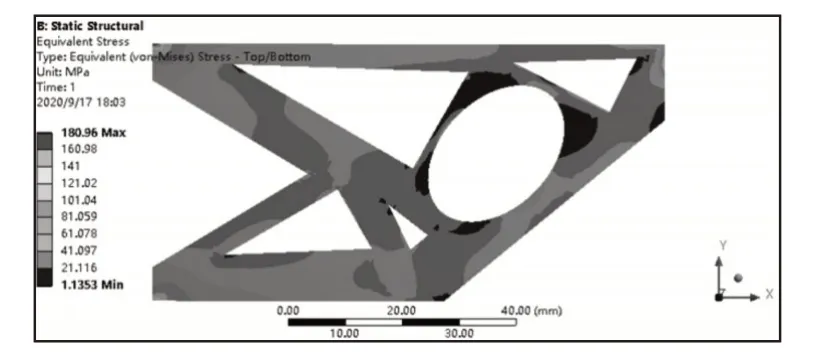
圖10 ANSYS中二次設計結構應力圖Fig.10 Stress Graphic of Secondary Design Structure in ANSYS

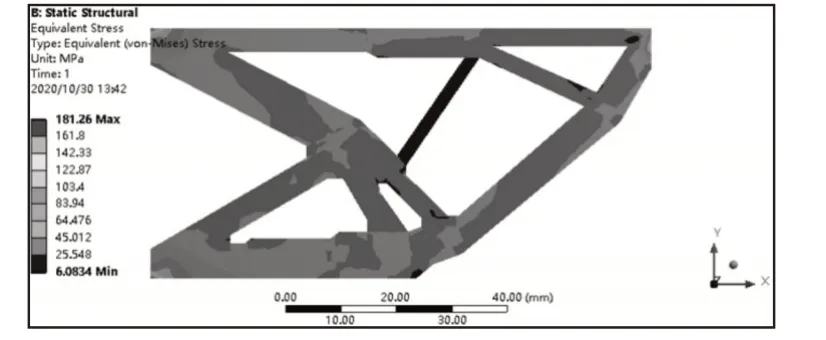
圖11 ANSYS中初始拓撲結構應力圖Fig.11 Stress Diagram of Initial Topological Structure in ANSYS

5 結論

以拓撲結構為基礎進行二次設計，將規則形狀孔洞取代拓撲結構中的不規則孔洞，從而使得優化后的結構便于加工。通過有限元方法計算出規則孔洞的形狀及大小與結構性能之間的關系并制作出樣本，通過樣本用神經網絡方法找到最佳性能值及其對應的孔洞參數，從而完成不規則孔洞的替換。實驗表明經過二次設計后的拓撲結構性能與初始拓撲結構性能相比，結構性能略微下降但增強了結構的易制造性。