應用狀態方程溫度對車輛油氣懸掛特性影響分析

李 鑫，張婕姝，羅德鋒，牛艷莉

（1.黃河科技學院，河南 鄭州 450063；2.鄭州宇通客車股份有限公司，河南 鄭州 450061）

1 引言

懸掛在車輛中起到傳力、緩沖沖擊、衰減振動的作用，是車架重要的組成部分。油氣懸掛結構簡單，內部的惰性氣體起到彈性作用，液壓油通過阻尼孔和單向閥的阻尼作用衰減振動；由于采用鋼制氣室，油氣懸掛適合更高的內部工作壓力，被廣泛應用于重型自卸車［1］。因此，通過對內部氣體和油液的物理狀態分析，獲取準確性更好的油氣懸掛模型，可提高油氣懸掛設計時的準確性和使用時的便捷性，具有重要研究意義。

國內外學者進行了一定的研究：文獻［2］認為密封圈摩擦力比較小，在建立油氣懸掛的數學模型時，對比忽略不計和作為常數處理的差異性，作為常數提高了結果的準確性；文獻［3］采用不同描述氣體溫度的狀態方程對懸掛輸出特性進行分析，并與理想狀態方程結果進行對比，提高了分析結果的準確性，但并未考慮缸筒和活塞桿本身的熱容；文獻［4］研究了溫度變化對液壓油動力粘度的影響，結果表明在油液溫度由20℃變化至80℃，油液動力粘度變化較大，設計時不能忽略；文獻［5］采用數學建模方法，分析不同溫度下，油氣懸掛的輸出力特征，以提高分析的準確性。

根據單氣室油氣懸掛的結構特點和輸出力特性，依據熱力學定律和BWR方程，對懸掛內部氣體和油液的熱力學性質進行研究；根據實際車輛的四分之一模型，搭建油氣懸掛加載試驗臺；基于數學模型和試驗臺工況，采用Simulink搭建仿真分析模型；分別施加靜載荷和周期性動載荷，獲取懸掛的輸出力特性和內部油液、氣體的溫度變化，分析溫度對輸出特性的影響；對比仿真分析和試驗測試結果，驗證數學模型的可靠性。

2 油氣懸掛數學模型

為了能夠更加方便研究懸掛內部特性，需要根據單氣室油氣懸掛的結構，進行示意圖簡化，如圖1所示。將油氣懸掛的阻尼孔簡化成固定節流孔，另兩個無彈簧形式單向閥小孔：鋼球開啟、閉合結構，當作單向閥處理［6］。

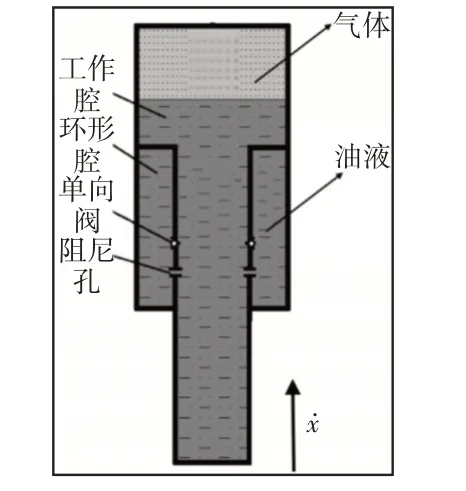
圖1 油氣懸掛原理圖Fig.1 Schematic Diagram of Hydro Pneumatic Suspension

車輛運動中，受到路面的激勵時，運動單元（活塞）和固定單元（缸筒）發生相對運動。此時，假設缸筒固定，則油氣懸掛輸出力數學方程：

式中：P1—工作腔氣體壓力，Pa；P2—環形腔壓力，Pa；A1—活塞面積，m2；A2—環形腔的面積，m2；Ff—密封件摩擦力，N。

2.1 氣體的熱力性質

2.1.1 理想氣體方程

在靜態緩慢加載的情況下，懸掛內部氣體可以近似為定質量系統，氣體熱力學過程可認為是等溫過程。因此懸掛靜行程設計、裝載與卸載過程中可將氣體近似為理想氣體等溫過程［7］，以此計算初始充氣體積和充油體積和懸掛的輸出力特性。

定溫過程的溫度保持不變，即T=常數。結合理想氣體狀態方程得定溫過程的過程方程為：

式中：p—氣體的絕對壓力，Pa；v—空氣的比體積，m3/kg；C—常數。由過程方程直接可得壓力與比體積的關系為：

2.1.2 真實氣體的熱力性質

氣體狀態方程中，B-W-R（Benedict-Webb-Rubin）方程應用較為普遍［8］，寫作：

式中：ρg—氣體密度，g/cm3；T—空氣的熱力學溫度，K；R—氣體常數；A0、B0、C0、a、b、c、α、γ—經驗常數。

2.2 油液的熱力性質

在溫度T下，油液的密度：

在溫度T下，油液的運動粘度：

式中：υ—油液的運動粘度，m2/s；μ—壓力p，溫度T時，油液的動力粘度；μ0—大氣壓下，溫度為T0時的動力粘度；α、λ—油液的粘壓系數和粘溫系數。

忽略壓強對粘度影響，其動力粘度函數即為：

聯立油液密度，式（5），得到油液的運動粘度：

2.3 懸掛中通過阻尼孔的液流狀態

由于自卸車的工作要求，負載和自重一般都很大，為了保證懸掛的強度要求，其懸掛活塞桿的壁厚較大，所以在活塞桿上開的阻尼孔的長徑比l/d通常大于4。懸掛處于拉伸狀態時（x?＜0），此時單向閥關閉，僅兩個阻尼孔作用。在輸入激勵頻率為0.5Hz，振幅50mm時，可計算出通過阻尼孔的液流雷諾數Re，如圖2所示。

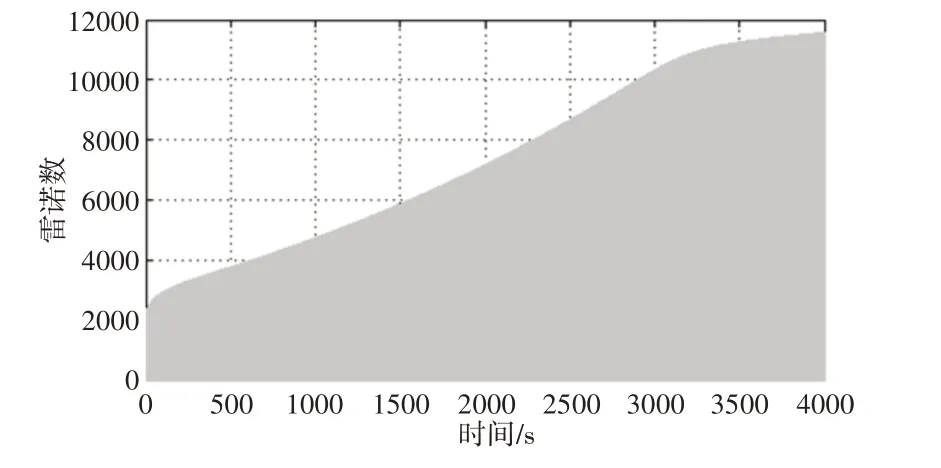
圖2 拉伸時液流雷諾數Fig.2 Reynolds Number of Liquid Flow During Stretching

通過兩個阻尼孔的流量為：

式中：Cd—阻尼孔流量系數；Ad—阻尼孔的過流面積，m2；ΔP—壓差，Pa。

小孔內液流速度為：

式中：d—阻尼孔直徑，m；A2—活塞桿面積，m2。

懸掛處于壓縮狀態時（x?＞0），單向閥與阻尼孔同時工作。此時計算出流經單向閥以及阻尼孔過流油液的雷諾數Re，如圖3所示。

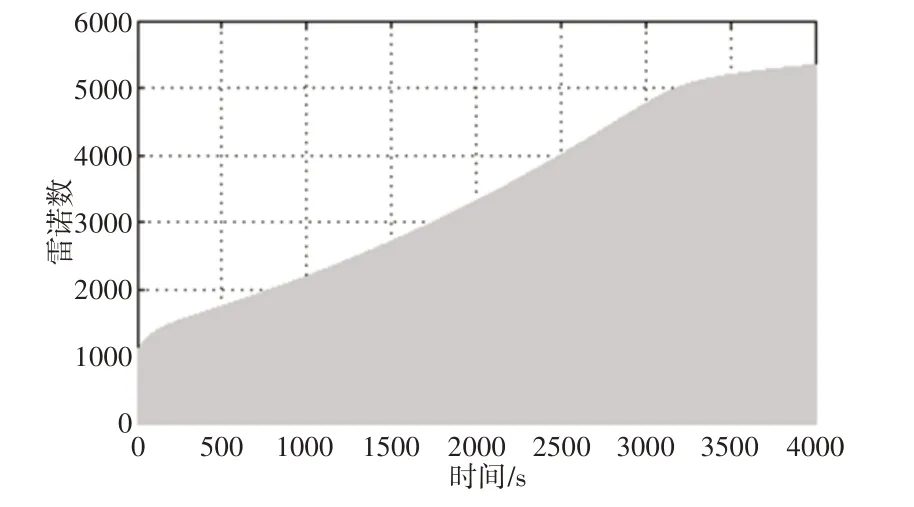
圖3 壓縮時液流雷諾數Fig.3 Reynolds Number of Liquid Flow During Compression

油液流經阻尼孔的流量為：

式中：Cz—單向閥流量系數；Az—單向閥的過流面積，m2。

鋼球在很小的壓力差下即可完全開啟或關閉，并且假定鋼球處于節流孔的中心線上，則，流經阻尼孔和單向閥的流量可表示為：

2.4 液體流動時的壓力損失

液體的流動狀態不同，所產生的沿程壓力損失也有所不同。層流時液體質點作有規律的流動，沿程壓力損失為：

式中：λ—沿程阻力系數。

湍流時，計算沿程壓力損失的公式在形式上與層流相同，但式中的阻力系數λ除了與雷諾數Re有關外，還與管壁的粗糙度有關，即λ=f（Re，Δ/d），式中：Δ—管壁的絕對粗糙度。

根據液壓油在懸掛內部流動特點，局部突變造成的局部壓力損失可以寫作：

式中：ξ—局部阻力系數。

綜合以上分析，將氣體、油液特性嵌入到單氣室油氣懸掛輸出力方程中，則可得油氣懸掛的熱力學數學模型：

3 油氣懸掛試驗臺和仿真模型搭建

為了更好的反映真實情況下油氣懸掛內部油、氣、缸筒和外界間的熱力學關系，根據實際車輛懸掛的運行特點，設計了支架加載試驗臺。原理圖，如圖4所示。

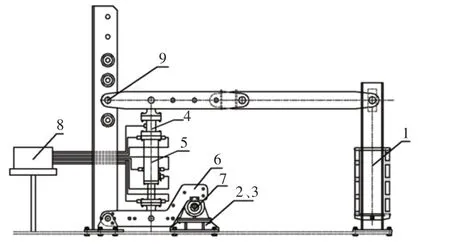
圖4 油氣懸掛試驗臺Fig.4 Hydro Pneumatic Suspension Test Bench

根據熱力學數據模型和試驗臺，基于Simulink搭建單個油氣懸掛的仿真分析模型，如圖5所示。

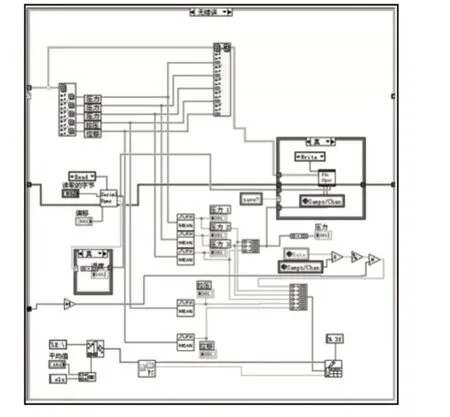
圖5 仿真模型Fig.5 Suspension Simulation Model

4 不同工況下性能對比分析

4.1 靜態加載

在空載或者滿載靜平衡位置時，懸掛內油液和氣體相對固定，體積比基本保持不變［9］。此時，油氣懸掛的初始充氣、充油體積即可確定。緩慢加載試驗中，油氣懸掛的初始充氣體積為0.15L，壓力為0.95MPa，懸掛行程為20mm，試驗和仿真結果，如圖6所示。懸掛能量的耗散主要是阻尼孔產生的阻尼力、密封件的摩擦力和氣體向外界的散熱。在靜態加載時，由于加載比較緩慢，阻尼孔所產生的阻尼力很小；同時氣體溫度變化也很小，可以認為氣體溫度保持不變，在這兩個壓力狀態之間的任意一點懸掛都能保持平衡，氣體處于平衡狀態，即氣體的能量不產生變化。

圖6 輸出力與位移關系曲線Fig.6 The Relationship Between Output Force and Displacement

4.2 周期性加載

對試驗臺進行周期性動態加載，載荷的初始參數為：內部的充氣壓力為1.0MPa，環境溫度為26℃，激勵頻率為0.5Hz、位移為120mm，激勵持續加載直至氣體溫度達到平衡狀態。

4.2.1 溫度影響對比分析

在氣體溫度達到平穩時即終止了周期性加載試驗，溫度變化結果曲線，如圖7所示。

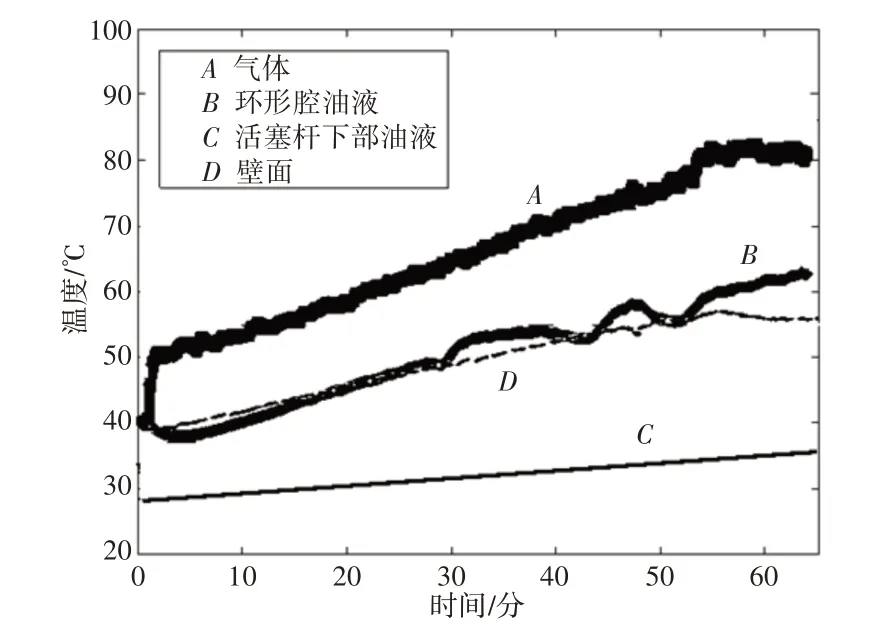
圖7 周期激勵下懸掛溫度變化曲線Fig.7 Suspension Temperature Change Curve Under Periodic Excitation

由圖中分析結果可知，施加周期性激勵后，油氣懸掛各部分的溫度均出現上升，經過一個小時左右的時間，氣體溫度上升最高達到82℃，油液溫度達到60℃左右；從變化趨勢可以看出，氣體溫度已經達到穩定，即與其他部分的熱交換達到平衡；活塞桿下部的油液也達到平衡狀態，保持在50℃，而環形腔內的油液溫度則仍保持上升的趨勢，達到熱交換平衡后，則會保持穩定。外界激勵停止后，懸掛自然冷卻。在外界激勵停止后，氣體溫度在一百秒內已下降至和環形腔油液溫度一致，然后氣體溫度隨著油液和缸筒的溫度下降趨勢降低。假設氣體在伸張行程中對外界不做功，只與外界進行熱量交換，并加大氣體與油液和缸筒的換熱系數，計算后所得結果，如圖8所示。

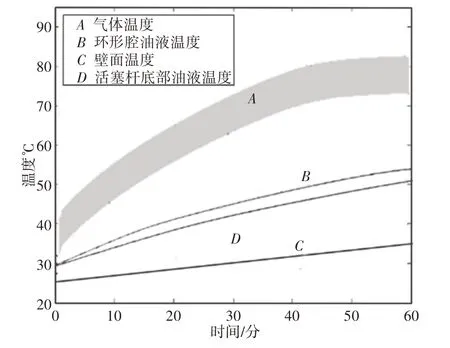
圖8 模擬獲得溫度變化曲線Fig.8 Temperature Curve Obtained by Simulation

圖中所示仿真結果可以知道，各部分溫度變化趨勢整體與試驗測試結果保持一致，活塞桿下部的油液穩定溫度達到48.5℃，試驗結果為50℃；壁面溫度為33℃，測試結果為34.6℃，所得最高溫度與試驗所得也相差很小，誤差控制在3%以內；氣體溫度達到穩定時的溫度為80.2℃，試驗測試為82℃，基本一致，而仿真獲得氣體溫度在周期內的變化幅度依然比試驗測得的數據要大。主要原因是氣體狀態較為復雜，換熱系數變化大；試驗傳感器采樣頻率未達到實際要求。在氣體溫度穩定后，考慮熱交換影響［10］，將試驗測得位移和氣體壓力代入仿真模型進行計算結果，如圖9所示。

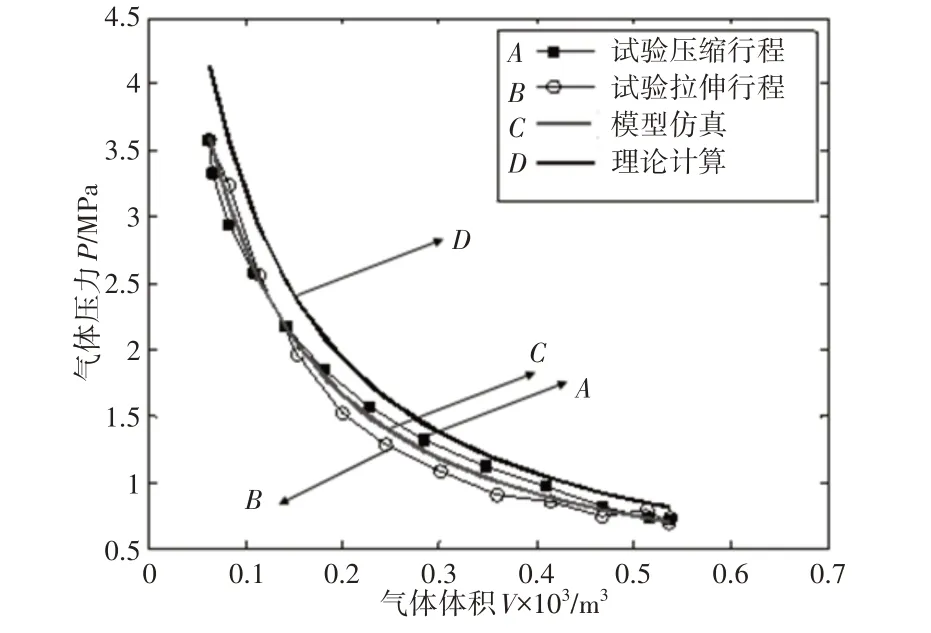
圖9 懸掛內氣體壓力與體積變化關系曲線Fig.9 Relationship Curve Between Gas Pressure and Volume Change

平衡位置時，氣體初始體積為0.362L，初始壓力為1MPa，質量為0.004kg，在最大行程時壓力為0.67MPa，當氣體溫升至80℃，計算最大行程時氣體壓力為0.79MPa，實際測得氣體最低壓力0.69MPa，考慮溫度變化，當懸掛伸張時溫度升高，氣體壓力不會低于0.79MPa。因為測得的試驗數據包含了理論計算時未考慮的傳感器誤差等各種不穩定因素，所以將所得氣體最低壓力數據代入仿真模型計算，結果顯示考慮溫度變化影響時，氣體PV曲線與試驗數據能較好的吻合。

4.2.2 懸掛環形腔和工作腔的壓差分析

周期性加載工況下，仿真分析和試驗測試獲得壓力變化曲線，如圖10所示。圖中結果可知，仿真結果與試驗結果變化趨勢保持一致，最大值均超過了3MPa，最小值在0.5MPa左右，二者之間的最大誤差為6.3%，表明仿真模型的準確性。

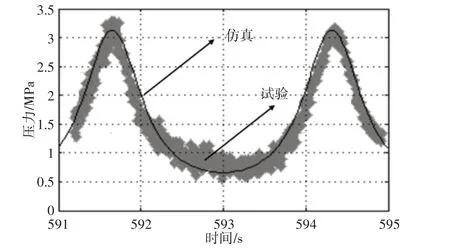
圖10 氣體壓力變化曲線對比Fig.10 Comparison of Gas Pressure Change Curves

5 結論

（1）靜態加載時，懸掛內部氣體的近似為理想氣體，氣體熱力學過程可近似為等溫過程；動態加載時，氣體為變質量系統，其所處熱力學過程為多變的過程；油液溫度升高，其動力粘度下降，懸掛承載力降低13%左右。

（2）承受激勵后，油液通過阻尼孔產生熱量，使得系統各部分溫度升高，達到平衡時，溫度穩定，溫升影響油液的粘度，進而對懸掛的輸出特性產生影響。

（3）基于對比，氣體壓力誤差控制在6.5%以內；在設計時，不可忽略內部氣體和油液溫升效應，可以聯合采用熱力學方程和B-W-R方程對油液和氣體熱力學特性進行描述，有效提升分析的可靠性。