旋翼翼型流動分離特性分析及高升力設(shè)計

王雪鶴,張子瀚,柴春碩,邢世龍,袁明川

(中國直升機(jī)設(shè)計研究所 直升機(jī)動力學(xué)全國重點(diǎn)實(shí)驗室,江西 景德鎮(zhèn) 333001)

0 引言

旋翼作為直升機(jī)重要的動部件,影響著直升機(jī)的飛行性能。對配置在旋翼上的翼型進(jìn)行針對性設(shè)計,能夠使旋翼氣動性能得到直接的提升。然而,直升機(jī)旋翼面臨的氣動環(huán)境十分復(fù)雜,設(shè)計指標(biāo)分解到旋翼翼型上后,在較寬速度范圍和升力系數(shù)范圍對其氣動性能有著近乎苛刻的性能要求。根據(jù)傳統(tǒng)的翼型設(shè)計指標(biāo)要求,旋翼翼型需要具備較高的最大升力(clmax)以滿足前飛和機(jī)動性能,較高的阻力發(fā)散馬赫數(shù)(Madd)以滿足前飛性能,較低的阻力系數(shù)(cd)以滿足前飛和懸停性能,較低的力矩系數(shù)(cm)以滿足操縱性能[1]。在上述設(shè)計指標(biāo)中,最大升力性能是旋翼翼型設(shè)計中不可妥協(xié)的一個重要性能指標(biāo)。如法國ONERA設(shè)計的OA系列旋翼翼型,在每代設(shè)計指標(biāo)中均對clmax提出了要求[2];俄羅斯設(shè)計的多代TsAGI旋翼翼型,有朝著“更高的clmax、更高的Madd”發(fā)展的趨勢[3]。因此,對失速特性的研究和提高最大升力系數(shù)成為旋翼翼型設(shè)計的重要方向之一。

在翼型失速機(jī)理分析方面,國外Katarzyna Surmac[4]采用風(fēng)洞試驗和CFD的方法,對SSC-A09翼型的失速后的流場特性進(jìn)行了專門的分析,CFD計算結(jié)果和油流顯示結(jié)果表現(xiàn)出了良好的一致性,均在大攻角時觀察到上表面分離渦的出現(xiàn)。國內(nèi)有文獻(xiàn)[5]闡述了翼型流動分離的三種類型,但文中沒有涉及分離流場的動態(tài)變化。有關(guān)翼型失速的流動機(jī)理分析常見于翼型動態(tài)特性研究的相關(guān)文獻(xiàn)[6]中。但從旋翼翼型設(shè)計的角度,首先關(guān)注的是靜態(tài)失速特性[7],因此需要設(shè)計人員對旋翼不同剖面的旋翼翼型靜態(tài)失速特性具有深入的認(rèn)識。

文獻(xiàn)[5]總結(jié)了國外設(shè)計人員提高固定翼翼型最大升力的方法,概括起來主要是采用了較大的前緣半徑和后部彎度。但對于旋翼翼型,較大的前緣半徑會導(dǎo)致高馬赫數(shù)阻力和阻力發(fā)散馬赫數(shù)激增;較大的彎度也會導(dǎo)致較高的低頭力矩。上述方法無法很好地滿足旋翼翼型設(shè)計要求。國內(nèi)研究人員在旋翼翼型設(shè)計方面,大多通過數(shù)值優(yōu)化手段將最大升力作為優(yōu)化目標(biāo)之一。孫俊峰等[8]采用基于進(jìn)化算法的多目標(biāo)優(yōu)化方法和Kriging代理模型,分別將0.3Ma、0.4Ma、0.5Ma的最大升力系數(shù)作為優(yōu)化目標(biāo)之一,對OA309翼型進(jìn)行了優(yōu)化設(shè)計,得到增升減阻的翼型結(jié)果;楊慧等[9]采用基于Kriging代理模型的優(yōu)化算法,將0.4Ma最大升力系數(shù)作為優(yōu)化目標(biāo)之一,對OA209翼型開展了多目標(biāo)優(yōu)化設(shè)計。盡管采用數(shù)值優(yōu)化方法可以得到滿足最大升力目標(biāo)的翼型結(jié)果,但在設(shè)計過程中,由于缺少對提高旋翼翼型最大升力的機(jī)理認(rèn)識,優(yōu)化結(jié)果對工程設(shè)計的指導(dǎo)意義有限。

本文選取兩種具有代表性厚度的旋翼翼型,開展旋翼翼型流動分離特性數(shù)值模擬分析,旨在揭示不同厚度翼型的失速特性及流動機(jī)理,并據(jù)此開展旋翼翼型失速特性參數(shù)影響研究。

1 數(shù)值模擬方法及驗證

1.1 流動控制方程

在連續(xù)介質(zhì)的假設(shè)下,忽略徹體力和熱源,二維可壓縮非定常N-S(Navier-Stokes)方程的表達(dá)式如下:

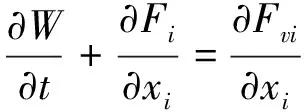
(1)

式中

式中,ρ為流體密度,ui為流體速度,p為壓力,E為單位質(zhì)量總能,τij為粘性應(yīng)力張量,δij為克羅尼柯爾符號。

為較好地模擬翼型大攻角分離流動,本文采用Menter[10]發(fā)展的k-ωSST模型對控制方程進(jìn)行封閉。

1.2 NACA0012翼型流場求解

為驗證本文采用的數(shù)值模擬方法,首先對NACA0012翼型的流場進(jìn)行求解,并與試驗結(jié)果對比。經(jīng)過網(wǎng)格收斂性研究(粗、中、密網(wǎng)格量分別為1.48萬、2.79萬、5.4萬),采用網(wǎng)格量為2.79萬的O型網(wǎng)格進(jìn)行CFD計算,網(wǎng)格第一層高度5×10-6,遠(yuǎn)場為50倍弦長,如圖1所示。

圖1 NACA0012翼型CFD計算網(wǎng)格

圖2給出了Ma=0.3,Re=6×106條件下NACA0012翼型在不同攻角下的壓力分布定常計算結(jié)果與試驗結(jié)果[11]的對比。壓力分布計算結(jié)果與試驗數(shù)據(jù)吻合良好。

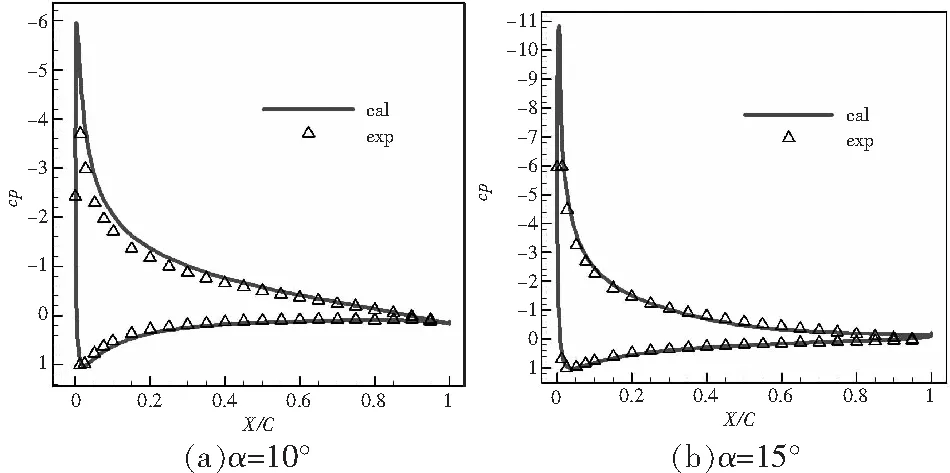
圖2 NACA0012翼型壓力分布計算與試驗結(jié)果對比(Ma=0.3,Re=6×106)

圖3給出了NACA0012翼型在Ma=0.15,Re=6×106時的升、阻力系數(shù)定常計算結(jié)果與試驗數(shù)據(jù)[12]的對比,并補(bǔ)充了失速攻角附近的非定常計算結(jié)果。考慮到翼型失速后,試驗結(jié)果本身受三維效應(yīng)的影響較大,因此最大升力系數(shù)的計算值與試驗數(shù)據(jù)存在差別,不過兩者的失速攻角十分接近。

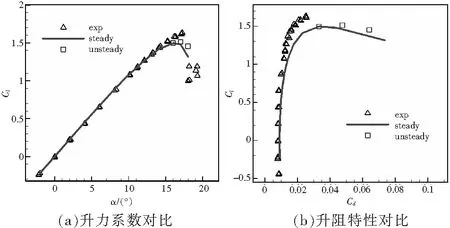
圖3 NACA0012翼型升、阻力計算與試驗結(jié)果對比(Ma=0.15,Re=6×106)

總體上,CFD計算結(jié)果與試驗數(shù)據(jù)吻合良好,驗證了本文采用的數(shù)值模擬方法的可靠性。

2 OA212翼型流動分離特性分析

采用定常RANS方法計算OA212翼型在不同攻角下的流場,計算狀態(tài)為Ma=0.3,Re=6×106,獲得力系數(shù)曲線,如圖4所示。定常計算結(jié)果顯示,翼型在15°攻角之后失速。

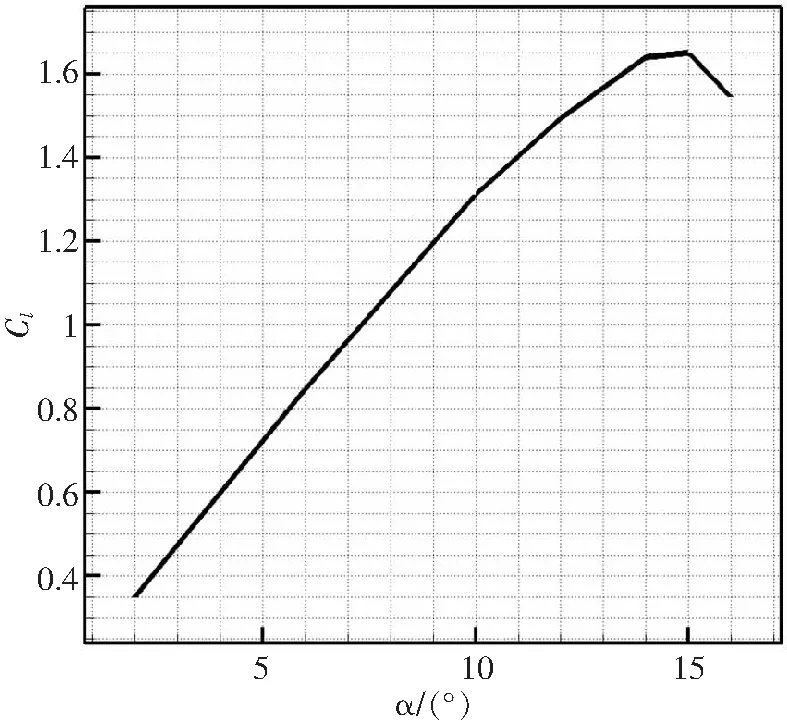
圖4 OA212翼型升力系數(shù)定常計算結(jié)果(Ma=0.3,Re=6×106)

由于失速攻角附近翼型繞流出現(xiàn)分離流動,為模擬流動分離后流場的變化情況,本文在翼型失速攻角附近采用非定常計算方法求解翼型的流場。計算時間步長取0.002 s,時間步數(shù)取1000步,獲取翼型在2 s時間內(nèi)的瞬時流場。

圖5、圖6分別給出了OA212翼型在16°、18°攻角的瞬態(tài)流場。可以看到,OA212翼型在攻角為16°時,后緣分離區(qū)域在0.4 s后即形成穩(wěn)定的分離渦形態(tài);隨著攻角增加到18°,后緣分離區(qū)域向前緣擴(kuò)展,但依舊能夠保持穩(wěn)定的渦結(jié)構(gòu)。

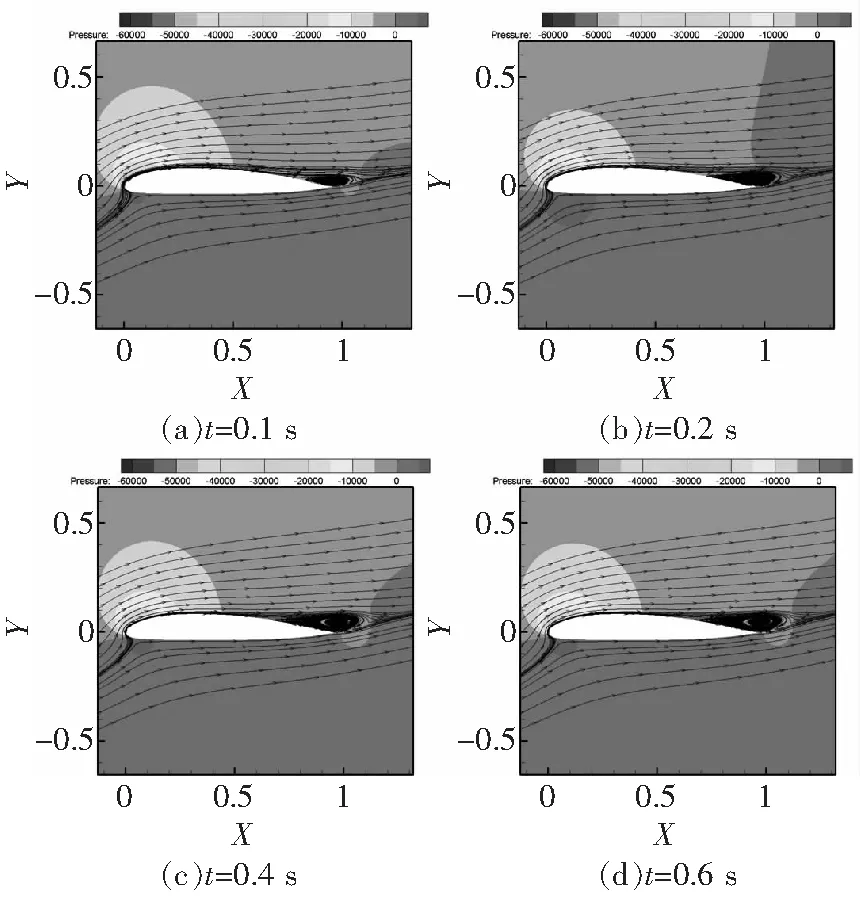
圖5 OA212翼型16°攻角瞬態(tài)流場

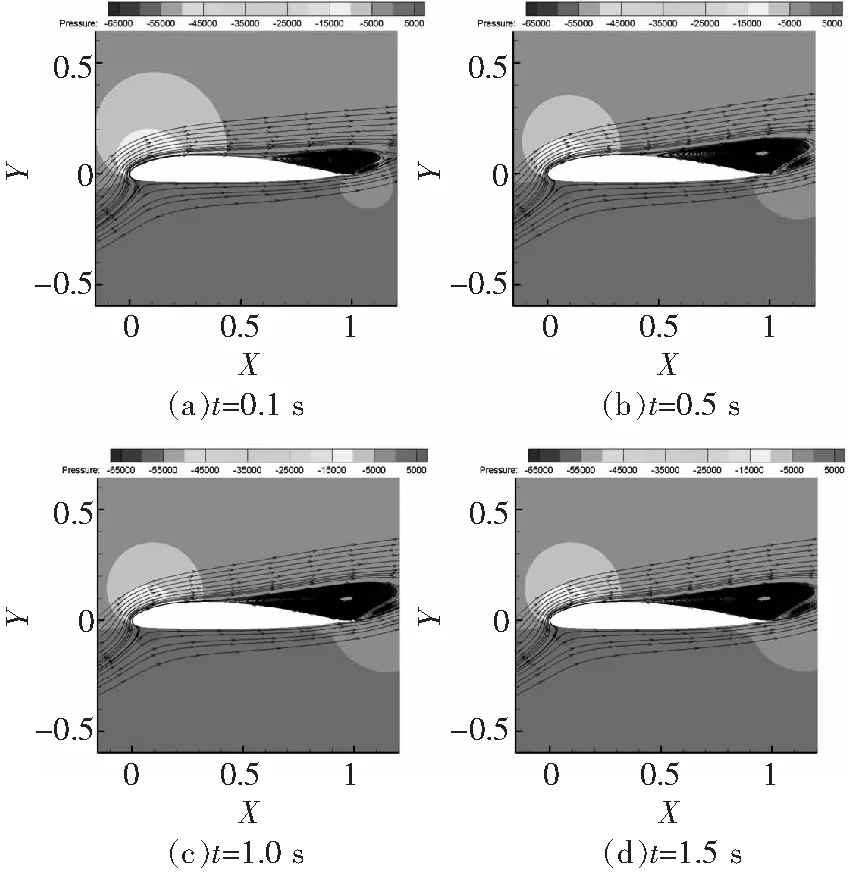
圖6 OA212翼型18°攻角瞬態(tài)流場(Ma=0.3,Re=6×106)

從失速形態(tài)可以看出,OA212翼型的失速由后緣分離開始;隨攻角增加,分離區(qū)域向前緣擴(kuò)展;分離過程相對穩(wěn)定,對應(yīng)著和緩的失速現(xiàn)象。

3 OA206翼型流動分離特性分析

采用定常RANS方法計算OA206翼型在Ma=0.3,Re=6×106的力系數(shù)曲線,從曲線結(jié)果中判斷失速攻角在9°附近,如圖7所示。其中,由于失速后受非定常分離流動的影響,10°攻角的升力系數(shù)值取迭代過程中的平均值。

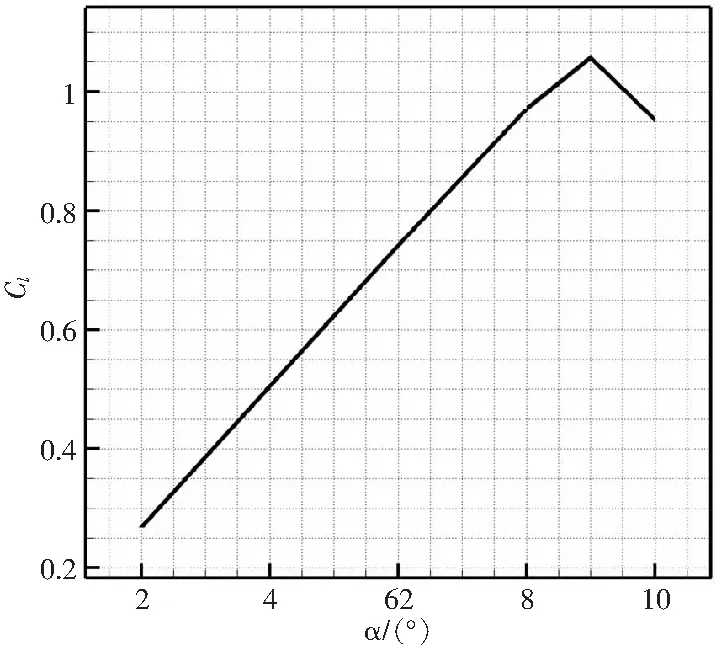
圖7 OA206翼型升力系數(shù)定常計算結(jié)果(Ma=0.3,Re=6×106)

圖8、圖9分別給出了OA206翼型在9°、10°攻角的瞬態(tài)流場。9°攻角時,翼型表面始終維持著附著流動。但當(dāng)增加到失速攻角10°后,從圖9中可以看到,流動從0.14 s開始前緣出現(xiàn)明顯的分離渦,然后分離區(qū)域擴(kuò)大并向后移動,直至分離渦脫落;0.42 s時前緣再次形成分離渦,上表面的分離渦表現(xiàn)出周期性脫落的性質(zhì)。與OA212翼型不同,OA206翼型分離渦脫落的過程使得翼型上表面階段性地處于大范圍分離狀態(tài),翼型的升阻力和力矩變化劇烈,表現(xiàn)出明顯的非定常特性。

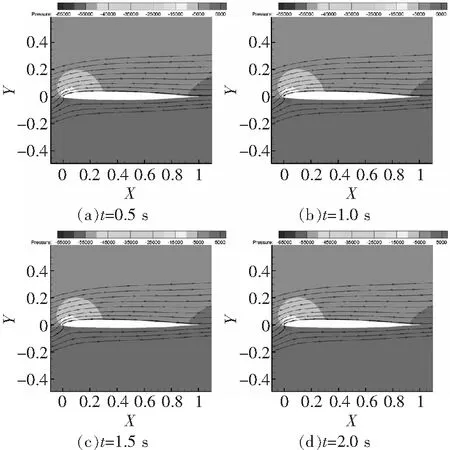
圖8 OA206翼型9°攻角瞬態(tài)流場(Ma=0.3,Re=6×106)

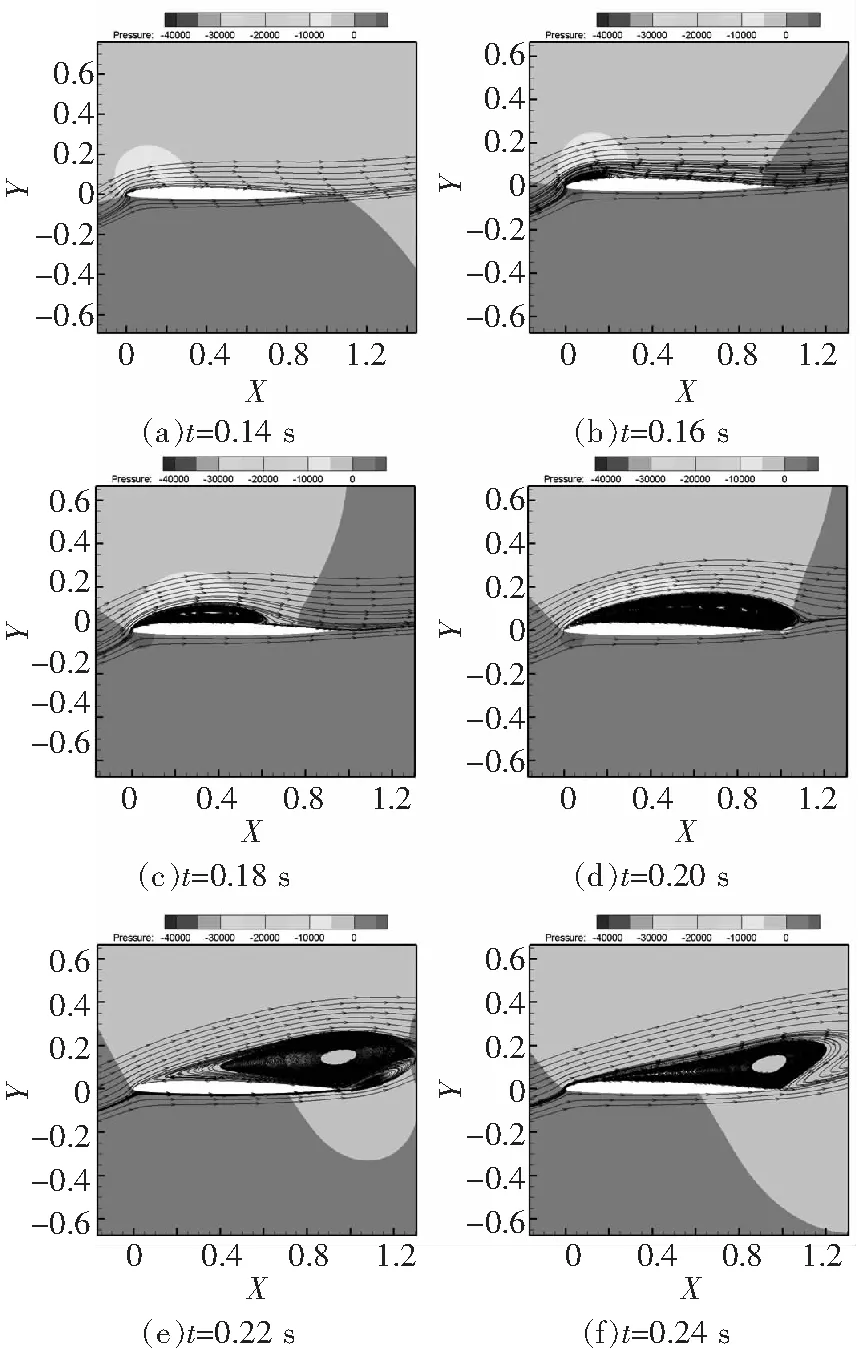
圖9 OA206翼型10°攻角瞬態(tài)流場(Ma=0.3,Re=6×106)

常規(guī)直升機(jī)旋翼槳尖處薄翼型在后行側(cè)的來流馬赫數(shù)常在0.4以上,因此增加OA206翼型0.4Ma的失速流場分析。通過靜態(tài)計算結(jié)果判斷,翼型此狀態(tài)下在8°攻角后失速,此處不再贅述。

圖10和圖11分別給出了OA206翼型在Ma=0.4,Re=6×106時8°、9°攻角的瞬態(tài)流場。在8°攻角時,翼型前緣附近出現(xiàn)小分離泡,但始終維持在前緣,并未向后擴(kuò)展,因而此時翼型并未失速。在9°攻角時,OA206翼型出現(xiàn)了周期性的渦脫落,非定常特性顯著。

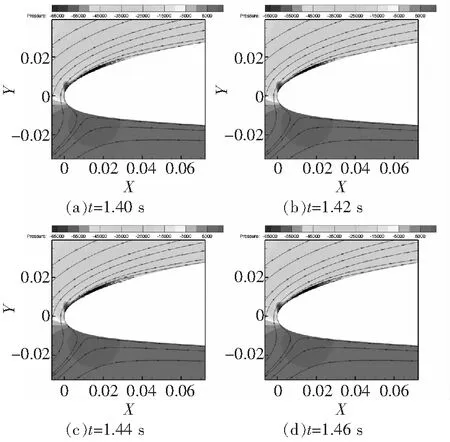
圖10 OA206翼型8°攻角瞬態(tài)流場(Ma=0.4,Re=6×106)

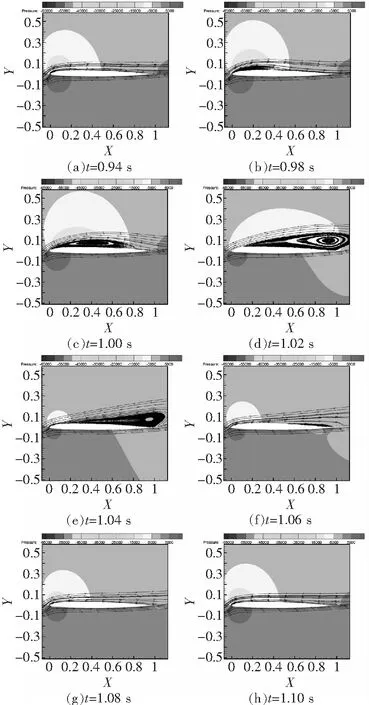
圖11 OA206翼型9°攻角瞬態(tài)流場(Ma=0.4,Re=6×106)

4 流動機(jī)理分析

提取OA212、OA206翼型在0.3Ma失速前的壓力分布及壓力梯度信息,分別如圖12和圖13所示。

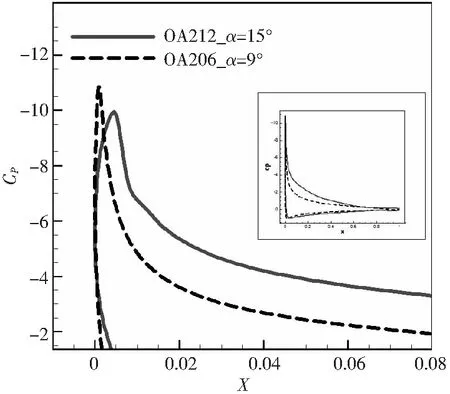
圖12 OA212、OA206翼型失速前上表面前緣附近壓力分布對比(Ma=0.3,Re=6×106)

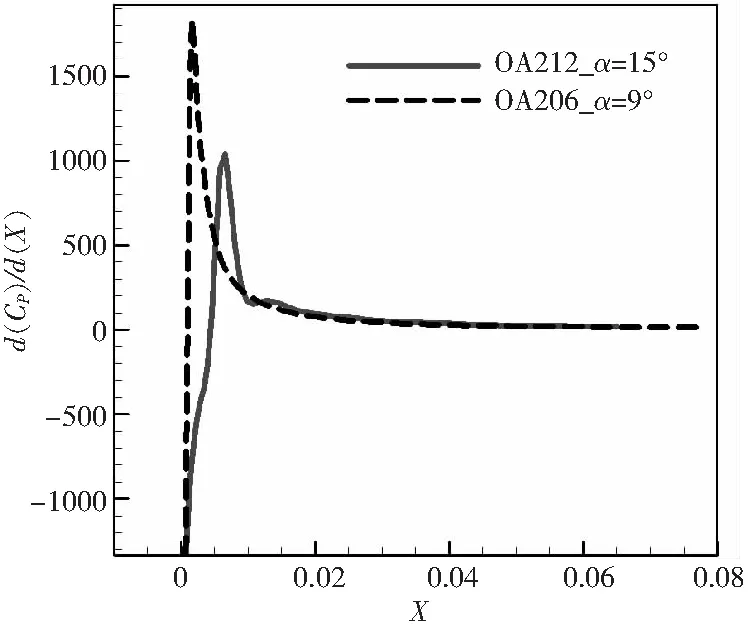
圖13 OA212、OA206翼型失速前上表面前緣附近壓力梯度對比(Ma=0.3,Re=6×106)

由于薄翼型前緣半徑較小,流動在靠近上表面前緣附近很短一段范圍內(nèi)經(jīng)歷了“流動加速使負(fù)壓達(dá)到峰值、強(qiáng)逆壓梯度使壓力恢復(fù)”的過程,空氣壓縮性較強(qiáng),流動難以維持附著狀態(tài),在前緣附近發(fā)生分離,再附后形成渦結(jié)構(gòu),向后緣移動并周期性脫落。

對厚翼型來說,盡管進(jìn)入失速狀態(tài)前在前緣同樣有著較高的負(fù)壓峰值,但負(fù)壓增長的速度相對緩慢,且經(jīng)過翼型前部外形曲率起到的氣流加速作用,故而上表面壓力分布不但梯度更小,而且峰值點(diǎn)向后延伸了一段距離,有效緩解了前緣的氣流分離趨勢。

由于曲率變化相對更大,厚翼型在上表面較大的范圍內(nèi)均面臨著更強(qiáng)的逆壓梯度,如圖14所示。翼型后緣氣流在逆壓梯度的作用下,最終難以維持附著流動而發(fā)生后緣分離。厚翼型的流動分離是一種從后緣向前緣發(fā)展的相對穩(wěn)定的過程,一般情況下不具備在前緣誘發(fā)分離的條件。

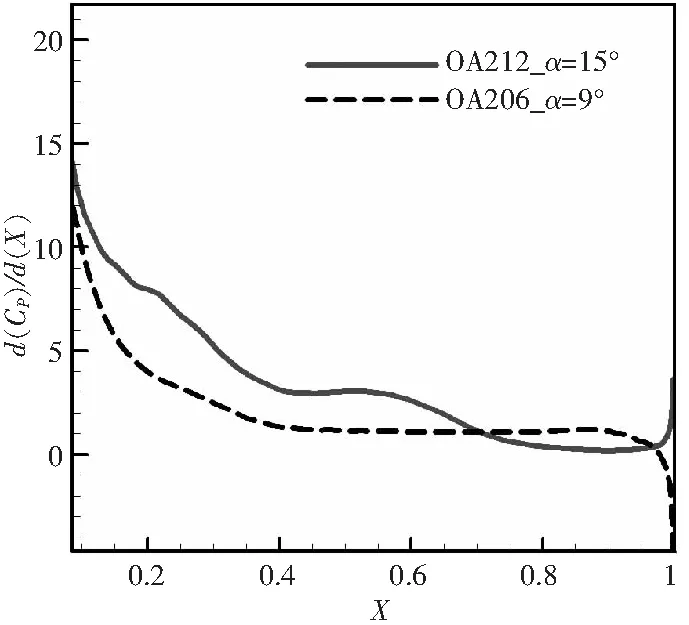
圖14 OA212、OA206翼型失速前上表面中后段壓力梯度對比(Ma=0.3,Re=6×106)

5 旋翼翼型失速特性參數(shù)影響分析

5.1 OA212翼型失速特性參數(shù)影響分析

根據(jù)前文分析內(nèi)容可知,12%相對厚度的翼型,失速由后緣分離起始。升力的降低主要由后緣分離渦導(dǎo)致。提高最大升力應(yīng)該主要從如何抑制后緣分離流動入手。

在OA212翼型的基礎(chǔ)上,增加前部(約0.1倍弦長處)曲率,降低前緣負(fù)壓峰值的同時抬高前部壓力曲線;在后緣流動分離區(qū)域(0.8倍弦長處),增加翼型局部曲率,減小翼型后緣的反彎度。修改后的外形和壓力分布對比如圖15、圖16所示。

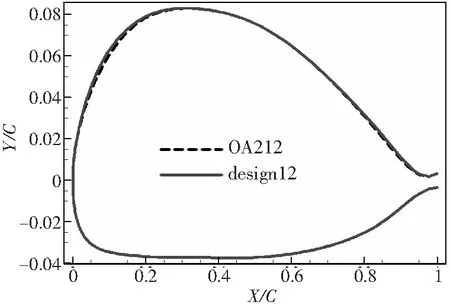
圖15 12%厚度翼型設(shè)計前后外形對比

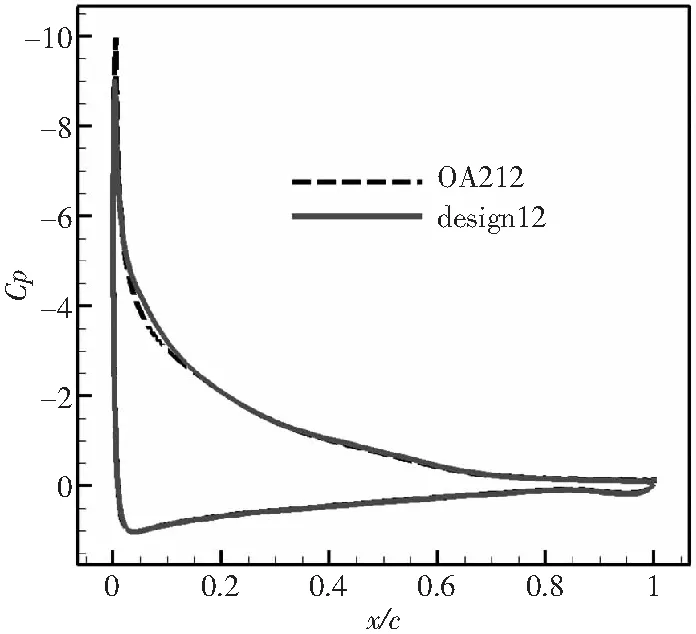
圖16 12%厚度翼型高升力設(shè)計前后壓力分布對比(α=15°,Ma=0.3,Re=6×106)

圖17、圖18給出了高升力設(shè)計前后旋翼翼型在Ma=0.3,Re=6×106時的定常計算升力系數(shù)曲線和升阻極曲線對比。設(shè)計翼型相比基準(zhǔn)OA212翼型,最大升力系數(shù)明顯提升,在發(fā)生分離流動的大攻角附近減阻效果明顯。

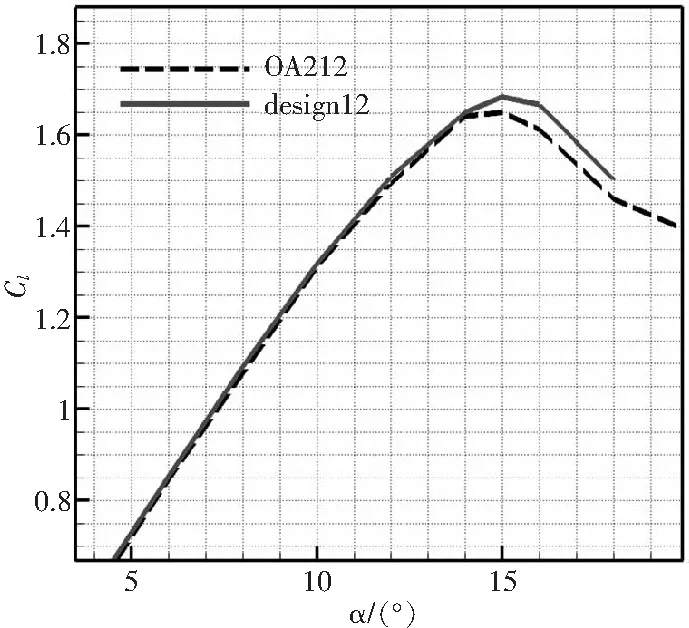
圖17 12%厚度翼型高升力設(shè)計前后升力系數(shù)曲線對比(Ma=0.3,Re=6×106)

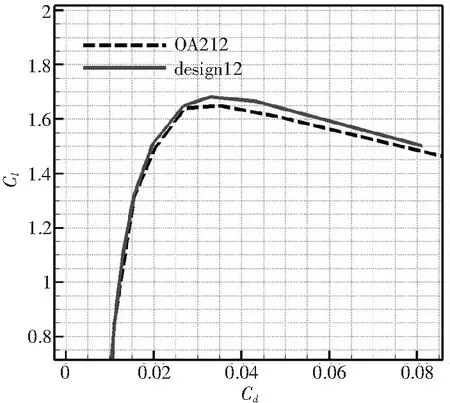
圖18 12%厚度翼型高升力設(shè)計前后升阻極曲線對比(Ma=0.3,Re=6×106)

圖19、圖20分別給出了12%厚度翼型在0.3Ma、0.4Ma達(dá)到最大升力時的定常流場對比。可以看到,設(shè)計翼型通過抑制后緣分離流動,有效提高了最大升力系數(shù)。

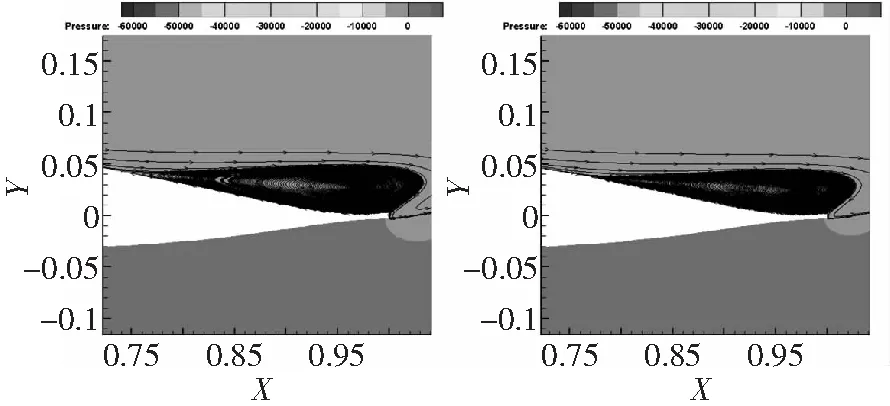
圖19 12%厚度翼型后緣分離流場對比(左:OA212,右:design12;α=15°,Ma=0.3,Re=6×106)

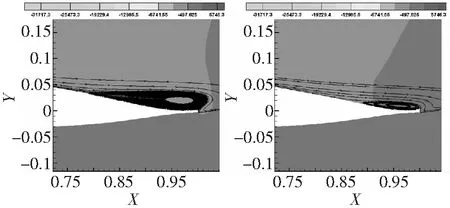
圖20 12%厚度翼型后緣分離流場對比(左:OA212,右:design12;α=12°,Ma=0.4,Re=8×106)

表1列出了12%相對厚度旋翼翼型修型前后的氣動性能對比,計算時保持相同的音速雷諾數(shù)(Re/Ma)。設(shè)計翼型的低馬赫數(shù)最大升力系數(shù)明顯提升,中等馬赫數(shù)的阻力和零升阻力發(fā)散馬赫數(shù)基本維持,力矩系數(shù)提高0.005。設(shè)計翼型在后部減小了翼型反彎度,因此在提高最大升力的同時,引起了低頭力矩系數(shù)的增加。由此可見,在改善旋翼翼型后緣分離特性時,需要綜合考慮對力矩特性的影響。

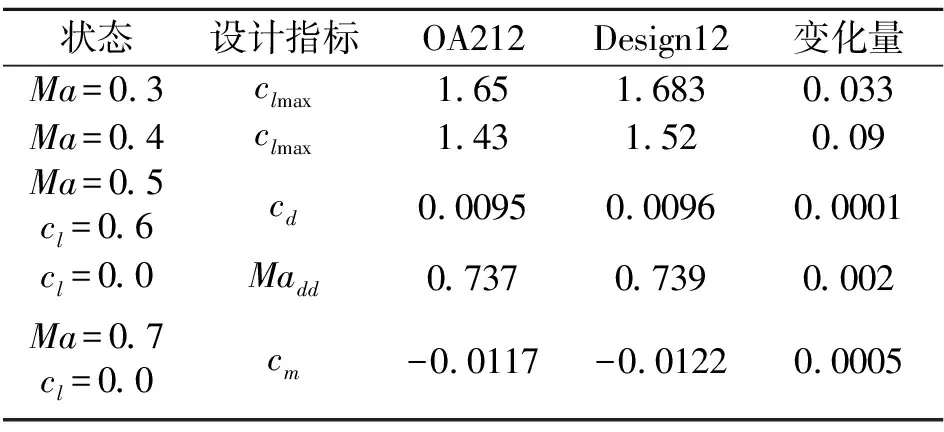
表1 12%相對厚度翼型設(shè)計前后氣動性能對比

5.2 OA206翼型失速特性參數(shù)影響分析

薄翼型前緣發(fā)生分離后即表現(xiàn)出顯著的非定常特性,常規(guī)手段難以有效控制分離后的流場。因此,結(jié)合失速前的流場特性進(jìn)行設(shè)計,是提高翼型最大升力的有效手段。

薄翼型具有在前緣很短的一段距離即達(dá)到負(fù)壓峰值的固有特性。因此,在翼型上表面前部適當(dāng)調(diào)節(jié)曲率:一則降低前緣附近壓力梯度,以維持失速攻角;二則增加壓力分布曲線面積,以提高失速前升力系數(shù)。此外,增加翼型中后部彎度也可以提高最大升力,但會增加力矩系數(shù),考慮到基準(zhǔn)翼型的力矩系數(shù)較小,因此不采用該種途徑。設(shè)計前后翼型外形對比如圖21所示。8°攻角壓力分布對比如圖22所示。

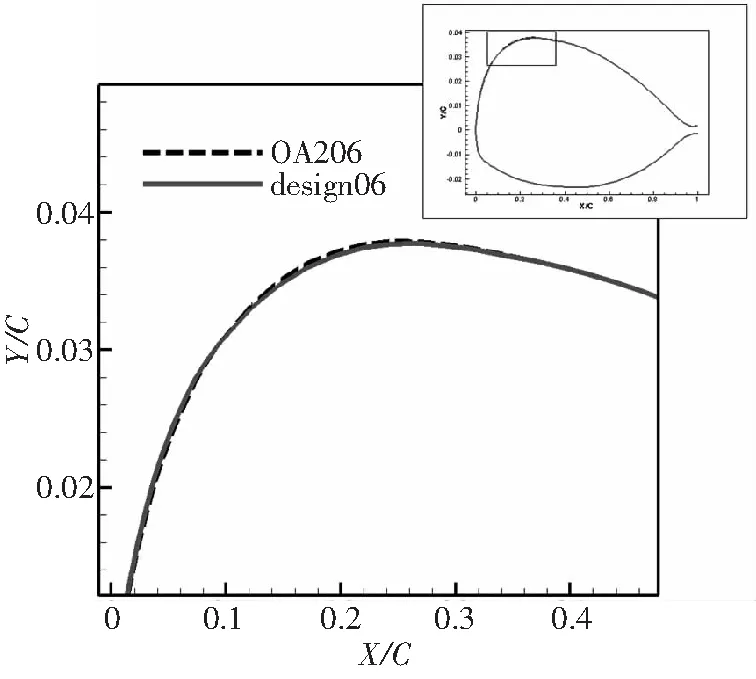
圖21 6%厚度翼型高升力設(shè)計前后外形對比

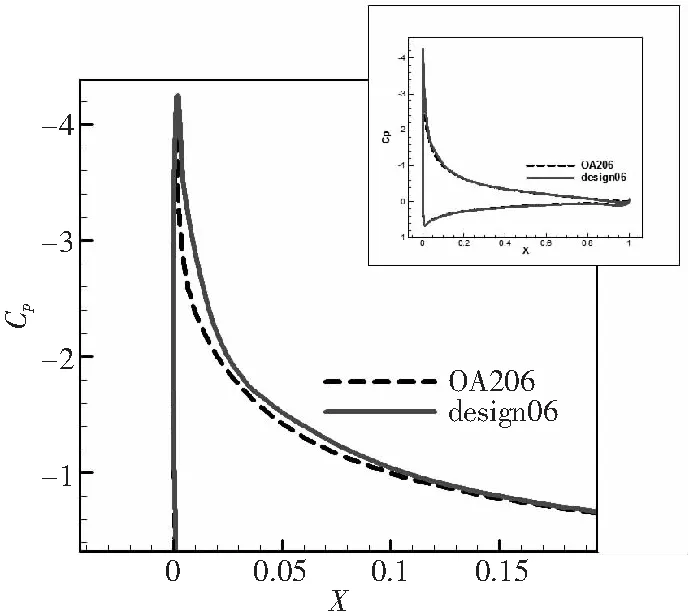
圖22 6%厚度翼型高升力設(shè)計前后壓力分布對比(α=8°,Ma=0.4,Re=6×106)

圖23、圖24給出了翼型在Ma=0.4,Re=6×106時的升力系數(shù)曲線和升阻極曲線的定常計算結(jié)果。翼型均在8°攻角后失速。與基準(zhǔn)OA206翼型相比,設(shè)計翼型的最大升力系數(shù)稍有提升,失速前阻力明顯減小。但由于上表面負(fù)壓峰值增加,當(dāng)馬赫數(shù)增加時,上表面激波強(qiáng)度增強(qiáng),導(dǎo)致高升力系數(shù)下的阻力增加,如圖25所示。因此,針對薄翼型,以提升最大升力系數(shù)為目標(biāo)進(jìn)行前緣外形改進(jìn)設(shè)計時,如采用改變前部曲率以增加前部壓力曲線面積的方法,則需要兼顧中、高馬赫數(shù)上表面激波強(qiáng)度。

表2列出了6%厚度翼型設(shè)計前后的氣動性能對比,音速雷諾數(shù)取1.5×107。設(shè)計翼型在0.4Ma的最大升力系數(shù)提升1.4%,阻力發(fā)散馬赫數(shù)和力矩特性基本維持,中等馬赫數(shù)的阻力系數(shù)增加了2.5%。由結(jié)果可見,單純依靠對薄翼型前緣局部外形作微調(diào)來提升最大升力系數(shù)的收益較小。

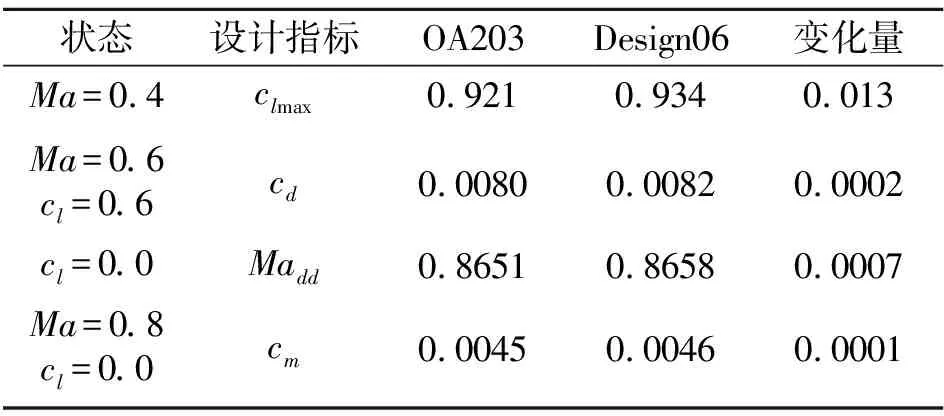
表2 6%相對厚度翼型設(shè)計前后氣動性能對比

6 結(jié)論

本文通過對兩個厚度的旋翼翼型開展數(shù)值模擬,分析了翼型的不同失速形態(tài),并從翼型表面壓力分布的角度解釋了引起翼型失速現(xiàn)象的機(jī)理。然后根據(jù)不同厚度翼型的失速機(jī)理,開展了兩個厚度旋翼翼型的失速特性參數(shù)影響研究。本文結(jié)論如下:

1) 厚翼型的失速現(xiàn)象通常是由后緣出現(xiàn)流動分離開始。失速初期表現(xiàn)為上表面后緣出現(xiàn)穩(wěn)定的分離渦結(jié)構(gòu);隨攻角增加,分離區(qū)域向翼型前緣方向擴(kuò)展,一般翼型失速特性較為和緩。

2) 薄翼型的失速通常由前緣流動分離引起。翼型上表面分離渦周期性脫落,使得上表面階段性地存在較大范圍的分離區(qū),導(dǎo)致翼型流場劇烈變化,表現(xiàn)出顯著的非定常特性。

3) 對于發(fā)生后緣分離的厚度較大的旋翼翼型,可以通過提高翼型前緣曲率,同時抑制后緣流動分離的方式,達(dá)到提高最大升力的效果;在調(diào)整后緣流動時要兼顧力矩特性。

4) 受限于最大厚度和前緣半徑,薄翼型的失速一般情況下皆由前緣失速主導(dǎo)。旋翼翼型設(shè)計時,首先需要避免前緣過早分離引發(fā)失速提前。在失速攻角不發(fā)生明顯變動的前提下,可以通過適當(dāng)增加壓力曲線前部面積來提升翼型最大升力并維持較低力矩,但需注意兼顧高馬赫數(shù)激波強(qiáng)度。