數值模擬的翼型氣動性能優化研究

曹利剛

(楊凌職業技術學院, 陜西 楊凌 712100)

1 前 言

風力機翼型的氣動特性可以通過數值模擬和風洞實驗的方法得到,隨著流體力學和計算機的快速發展,數值模擬方法已經成為一種常見的優化方法。與風洞試驗相比,數值模擬主要體現出適應性強、成本低、用時短等優點,但數值模擬依賴于實驗觀測和理論分析。

2 網格劃分方法

數值計算結果主要取決于網格劃分質量的好與壞,網格點的布局是網格生成的關鍵[1]。對于不規則邊界非結構化網絡適應性強,但是節點位置不能用一個固定的法則有序命名,網格生成的時間長,計算量大,離散方程求解速度很慢。對于結構化網絡,對計算區域的幾何形狀要求較多,單系統中的節點排列很有規律,相鄰點之間的關系清晰。本文利用HyperMesh軟件生成C型二維結構化網格并延展向延伸生成三維網格。

設計的弦長為1 m,以翼型的前緣頂點為中心,左邊區域選為半徑是12.5 m的半圓,右邊區域選為長25 m,寬20 m的長方形,延展向的厚度為10 cm。在翼型上共布置162個點,上、下表面各81個,上、下表面法向方向都布置50個節點,尾流方向布置60個節點,展向方向布置3個節點,平行網格尺寸是垂直網格尺寸的10倍。

對于二維流場,進口處的給定風速為邊界條件,出口處的壓力為邊界條件,翼型的表面是靜態無滑移壁面邊界。對于三維流場除設定與二維相同的條件外,還需要設置延展向翼型的兩個端面的對稱邊界條件。

3 NACA63-215氣動模擬

求解過程中采用Fluent軟件,初始條件設定為:風速10.6 m/s,雷諾數110萬,弦長1 m。把速度設定為進口邊界,壓力設定為出口邊界,展向對稱型邊界,無滑移壁面邊界。

根據參考文獻[2-3]對同種翼型的模擬數值分析可知,Spalart-Allmaras湍流模型是單方程模型,達到收斂所耗費的時間相對較少。該模型能更加詳細的反應流動參數變化,這對于具有層流流動的固壁湍流流動有良好的易收斂性和穩定性,計算翼型的氣動數值也相對更加精確。所以本文采用S-A模型,模擬迎角的范圍是[0°,20°],步長為2°,得到共計11組升力和阻力系數,如表1所示。升力和阻力系數的實驗值與模擬值比較如圖1所示,升阻比的實驗值和模擬值比較如圖2所示,攻角的單位都是度。

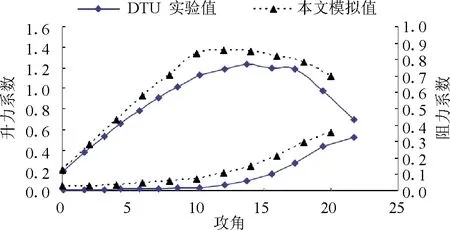
圖1 升力和阻力系數的實驗值與模擬值對照圖

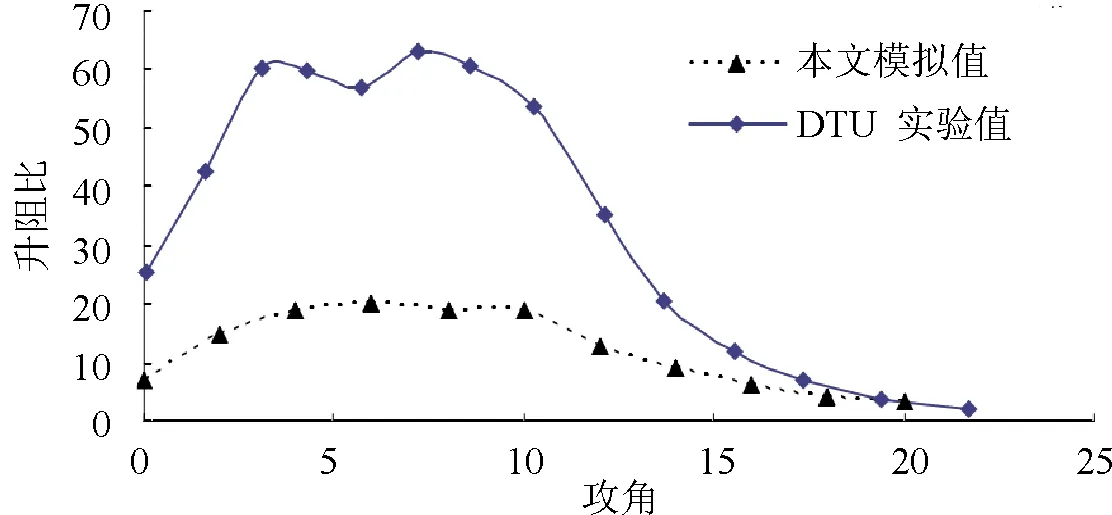
圖2 升阻比的實驗值和模擬值對照圖

表1 模擬得到的升力和阻力系數

從圖1可以看出實線連接的菱形點代表實驗值,虛線連接的三角形點代表本文的模擬值,模擬值總體比實驗值偏高,但變化規律基本相同,模擬升力系數在迎角是10°左右時達到了最大值,然后逐漸減小,DTU實驗值在迎角為14°時達到了最大值,然后減小。模擬的阻力系數值和實驗值基本吻合,都在10°左右時出現了拐點,然后快速增大。

從圖2可以看出由三角形點組成的模擬值普遍小于由菱形點組成的實驗值,模擬值和實驗值之間存在一定的差異,但變化規律基本相同。在4°～10°之間,升阻比的值較大且基本沒有變化,在10°以后兩個曲線都迅速下降,到達20°時重合。

綜上述所,可以看出整個計算模擬效果較好,基本與實驗值相同,尤其是在小角度時模擬升力系數和阻力系數時更為準確。

4 襟翼的DOE實驗分析

對于翼型的氣動優化過程,目前主要是翼型整體氣動外形優化,近年來也發展了一種新技術,就是在機翼的后緣附近安裝一個襟翼[4]。襟翼繞軸能向后下方偏轉,這樣就增加了機翼的彎度,這有利于提高翼型的升力和升阻比[5]。 本次實驗將以升力系數最大為設計目標,實驗過程中采用ANSYS中的DOE實驗設計模塊的數值模擬方法。

4.1 實驗步驟

NACA63-215后緣加簡單襟翼后,數值模擬的狀態如下:翼型的特征長度l=0.3;設計風速V=12 m/s;雷諾數設定為Re=0.24×106;簡單襟翼的寬度b=2 mm,高度h=4.5 mm,偏轉角q=90°;控制襟翼角度變化的形狀變量設置兩個,控制襟翼高度的形狀變量設置一個;襟翼的角度變化范圍是-45°至90°,襟翼的高度變化范圍為3 mm至9 mm,以升力系數最大為襟翼的優化目標。運用DOE實驗設計方法計算NACA63-215新增襟翼在高度和角度變化時翼型升力系數的變化。

4.2 實驗數據與分析

4.2.1 襟翼的高度不變 偏轉角變化 保持高度h=4.5 mm不變化,襟翼的偏轉角分別為45°、55°、65°、75°、85°、90°、95°、105°、115°。升力系數變化率、升阻比、升力系數和阻力系數變化統計如表2所示。從該表可以看出,在襟翼高度4.5 mm不發生變化時,隨著偏轉角從45°到135°每隔15°變化時升力系數由小變大再變小,在90°時達到了最大值。阻力系數變化規律和升力系數相同,在90°時達到了最大值。升阻比隨角度增加呈現先減小后增大的變化局勢,在90°時取得最小值。升力系數變化率也是由小變大,再由大變小。

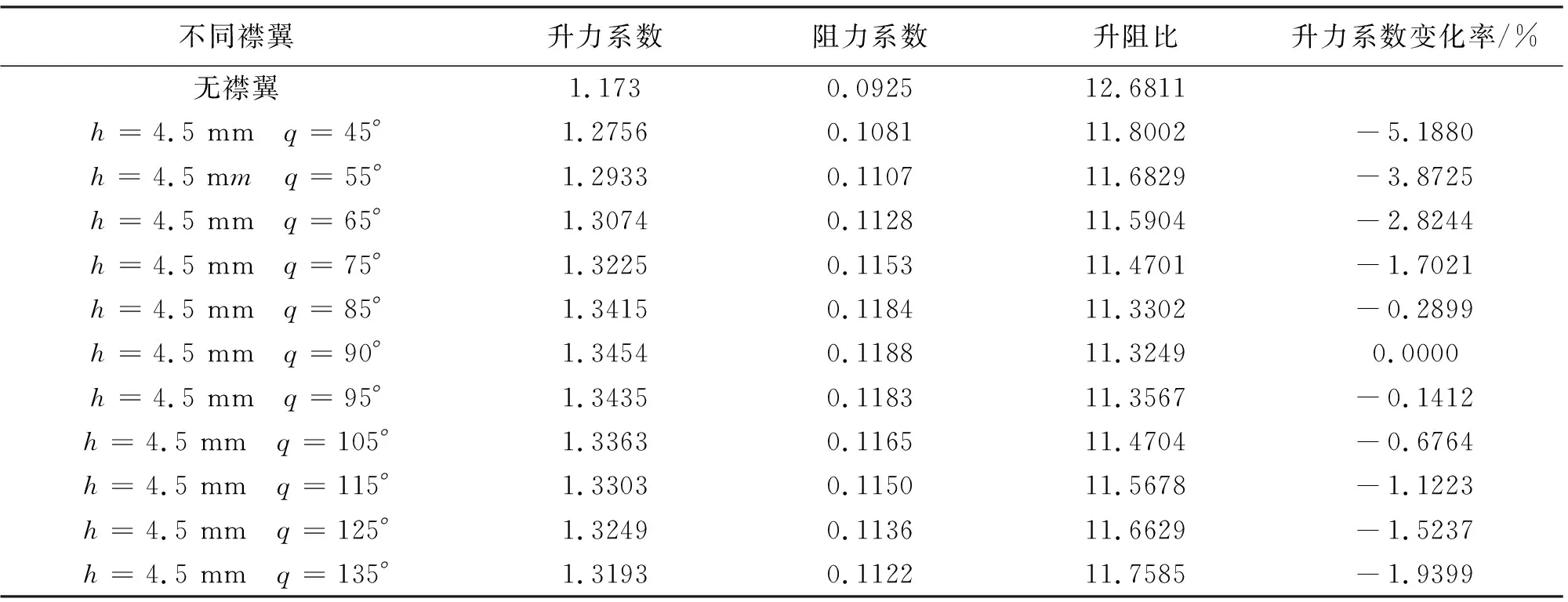
表2 不同偏轉角襟翼的氣動系數

4.2.2 襟翼的偏轉角不變 高度變化 保持偏轉角q=90°不變化;高度分別取3 mm、4 mm、4.5 mm、5 mm、6 mm、7 mm、8 mm和9 mm。升力系數變化率、升阻比、升力系數和阻力系數變化統計如表3所示。從表3可以看出,當偏轉角θ=90°不變化時,當襟翼的高度從3.0 mm到9.0 mm之間每隔1.5 mm變化一次,升力系數由小變大呈現單調增加的變化局勢,阻力系數也呈現了由小變大單調增加的變化局勢,升阻比呈現由大變小的單調減小變化局勢,升力系數變化率也呈現由小變大的單調增加局勢。

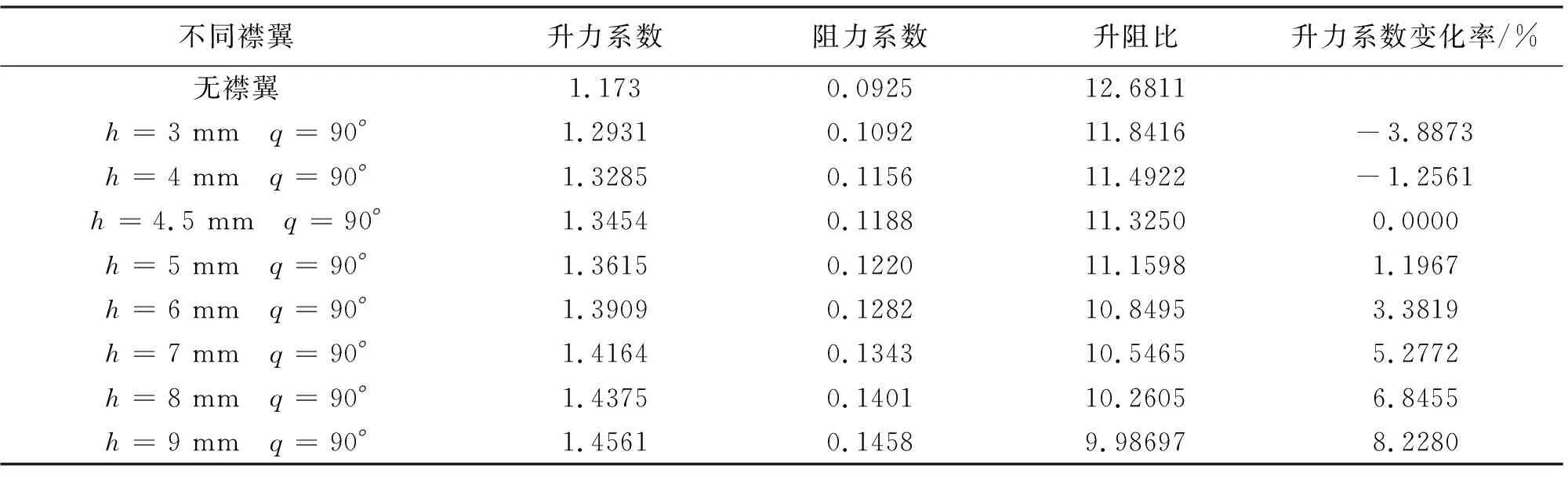
表3 不同高度襟翼的氣動系數

綜上可知,當襟翼的偏轉角θ=90°時,升力系數達到了最大值,升阻比達到了最小值。在θ=90°時,增加襟翼的高度,升力系數逐漸升高,升阻比由大變小,升力系數變化率由小變大。所以偏轉角為90°時,增加襟翼的高度有利于改善翼型的綜合性能。

4.3 壓力分布分析

不同襟翼時翼型壓力分布如圖3所示。得出,(a)、(b)、(c)三幅圖的襟翼高度不變,隨著偏轉角不斷增大,翼型下方深色陰影的面積由小變大,再由大變小,θ=90°時,翼型下方代表正壓力的深色陰影面積達到了最大值,此時襟翼受到的壓力最大,因此升力系數得到了最大的提高。翼型前緣圓球狀的大小沒有變化,說明翼型前緣受到的升力基本無變化。對照(b)圖和(d)圖得知兩幅圖的襟翼偏轉角度相同,(d)圖襟翼的高度h=9.0 mm,翼型下方圓球狀的面積大,(b)圖襟翼的高度h=4.5 mm,襟翼下方的圓球狀面積小,說明同樣的偏轉角時,在一定的范圍內,增加襟翼高度可以增加翼型的升力。

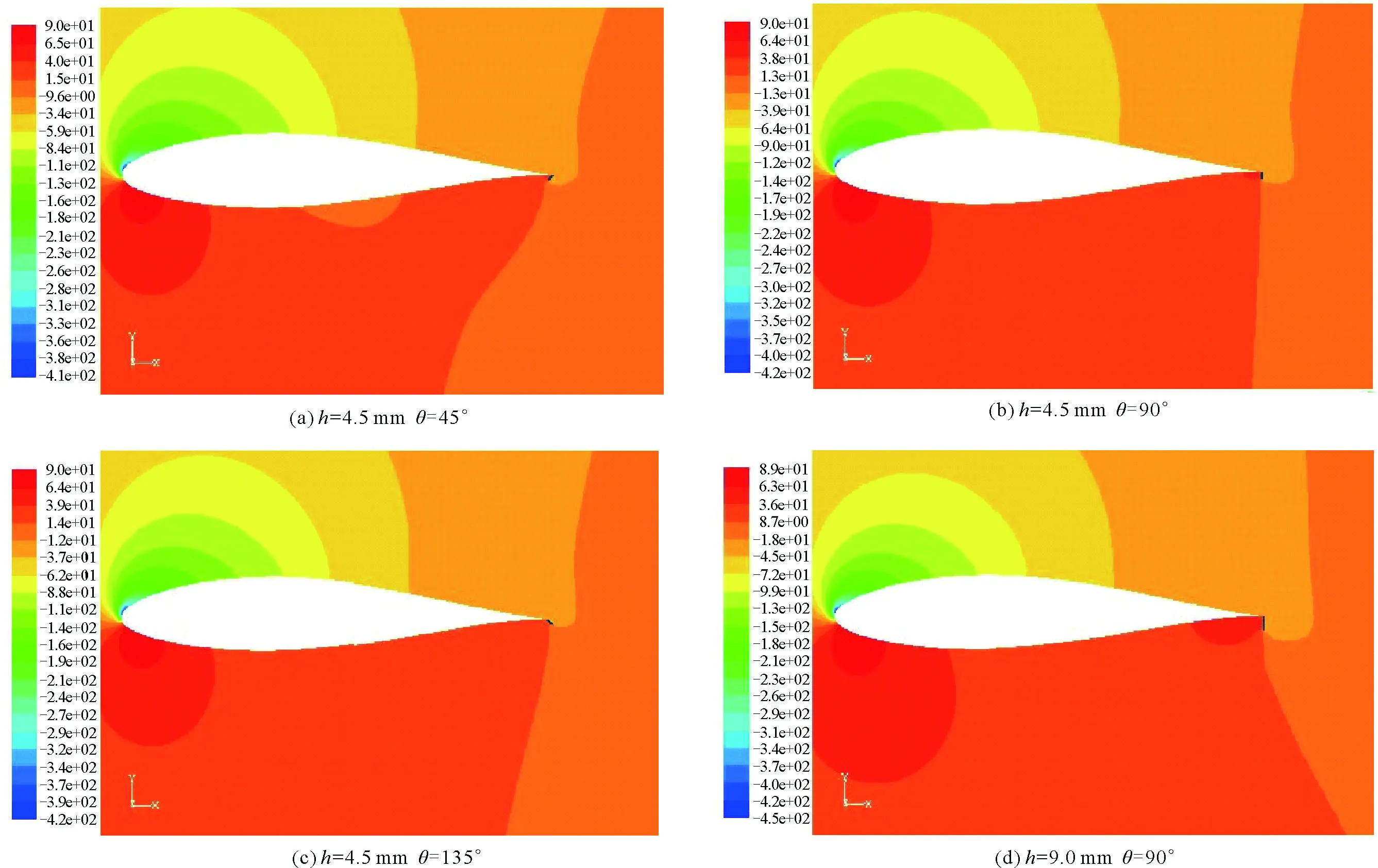
圖3 NACA63-215不同襟翼時翼型壓力分布圖

5 總 結

本文首先把NACA63-215翼型氣動模擬的數值與DTU實驗值進行對比,發現小角度攻角時模擬的升力系數和阻力系數非常準確。然后對襟翼DOE的多組數值模擬實驗數據分析后得知:偏轉角90°時,增加襟翼的高度有利于改善翼型的綜合性能,最后對翼型下方的壓力分布模擬圖形分析后同樣可得:偏轉角90°時,增加襟翼的高度可以增加翼型的升力,改善翼型的綜合性能,所以數值模擬的方法為翼型的氣動性能優化提供了理論支持。