基于ST-SVD與WOA-SVM模型的變壓器繞組松動故障診斷方法*

薛健侗, 馬宏忠

(河海大學 能源與電氣學院,江蘇 南京 211100)

0 引 言

變壓器作為電力遠距離輸送的核心設備,其正常運行是維持電網安全、可靠的關鍵,因此也是變電站運維的重點對象[1-2]。然而,變壓器繞組由于固有的運輸安裝過程中產生的輕微移位以及長期經受短路沖擊電流造成的松動變形情況,使得該原因導致的事故發生率成為首位[3-4]。因此,研究變壓器繞組松動故障診斷技術,及時發現、排查出變壓器繞組故障隱患,對變壓器穩定運行具有重要的現實意義[5-6]。

由于變壓器繞組松動與變壓器異常振動存在因果關系,因此目前振動法被廣泛應用于變壓器的故障診斷[7],基于變壓器振動信號的時頻分析一直是熱點。文獻[8]采用快速傅里葉變換(FFT)方法對變壓器振動信號進行處理,揭示了振動信號50 Hz分量及其部分倍頻分量等新特征頻率來反映變壓器內部繞組松動變形故障,并基于此建立了診斷模型,實現了繞組松動故障診斷與初步定位。文獻[9]采用希爾伯特-黃變換(HHT)方法,對變壓器振動信號經驗模態分解(EMD)后的各層本征模態函數(IMF)進行希爾伯特變換,以三維希爾伯特能量譜及邊界譜反映變壓器隱含的鐵心振動特征。文獻[10]基于小波變換方法,對變壓器開關切換產生的繞組振蕩波進行時頻特性分析,通過量化時頻信號特征反映變壓器繞組的機械狀態。上述信號分析方法都在處理變壓器振動信號方面取得了良好效果,但此類方法仍有其局限性,例如小波變換的母小波和分解層數的確定會直接影響信號分析效果,HHT對噪聲敏感容易導致結果誤差較大等。S變換(ST)是近年興起的一種時頻分析方法,其窗函數寬度隨信號頻率變化而變化,對信號的分辨率高且抗噪能力強,十分適合處理非平穩信號[11]。同時,奇異值分解(SVD)是一種成熟的矩陣特征提取技術,其已和多種時頻分析方法結合,應用于圖像處理、模式識別等許多領域[12]。

支持向量機(SVM)是一種常用的機器學習方法,在處理小樣本集分類時展現出獨特的優越性[13]。文獻[14]將鯨魚優化算法(WOA)引入SVM模型中對懲罰因子c與核函數參數g進行尋優,利用隨機森林(RF)特征優選構建變壓器油中溶解氣體特征向量,實現變壓器故障診斷模型的構建,驗證了WOA-SVM模型的優越性,實現了較好的應用效果。

綜上所述,本文提出一種基于ST-SVD與WOA-SVM模型的變壓器繞組松動故障診斷方法。首先采用S變換得到變壓器振動信號的時頻矩陣,經轉化為幅值矩陣后進行SVD得到相應的矩陣奇異值,然后定義特征奇異值并提取出來組成特征向量,最后采用WOA優化SVM的c、g參數,輸入訓練樣本構建WOA-SVM模型并對測試樣本進行分類診斷,通過與K-means聚類、SVM和粒子群優化(PSO)-SVM模型的診斷準確率進行對比,驗證了本文所提方法的有效性與可行性。

1 S變換和SVD

1.1 S變換原理

S變換是Stockwell等[15]于1996年提出的信號處理方法,其綜合了小波變換和短時傅里葉變換的特點,其窗函數與頻率相關,對噪聲不敏感,信號分辨率高,十分適合處理非平穩信號。

對于連續時間信號x(t),S變換如下:

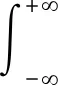
(1)

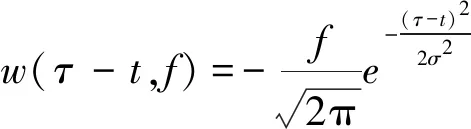
(2)

式中:w(τ-t,f)為高斯窗函數;t為平移因子;σ=1/f。

由此可以看出,S變換的高斯窗函數的寬度和高度隨著頻率f的變化而變化,因此在低頻段具有高頻率分辨率,在高頻段具有高時間分辨率[16]。

實際應用中,S變換需離散化處理,可表示為

(3)

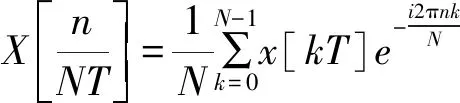
1.2 SVD特征提取

矩陣經過SVD得到的奇異值能夠充分表示矩陣包含的信息[17],因而廣泛應用于信號的特征提取。任意一個矩陣Mm×n,存在著正交矩陣Um×m和Vn×n,將其分解為

M=USVT

(4)

S=diag(σ1,σ2,…,σr,…,0)

(5)

式中:σ1,σ2,…,σr為矩陣M的奇異值。

變壓器振動信號經S變換后得到的是時頻矩陣,需將各元素求模后得到幅值矩陣再進行SVD。因此,得到奇異值σ1,σ2,…,σr反映的是所采集變壓器振動信號的特征量,并且由相應幅值矩陣唯一確定[18]。由于奇異值個數受到幅值矩陣行列數大小的影響,一般數量很多,因此需進一步處理從而突出變壓器振動信號在繞組正常與松動狀態下的相對變化[19]。本文選擇計算所有奇異值的最大值k1、平均值k2和標準差k3作為特征值。表達式如下:

k1=max(σ1,σ2,…,σr)

(6)

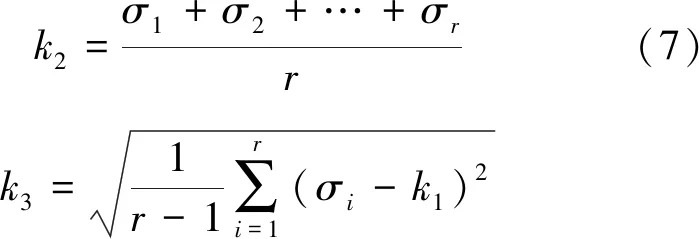
(8)

將三個特征值組成特征向量[k1,k2,k3],通過各元素的變化,反映變壓器繞組正常與松動狀態下的特征信息,作為本文故障診斷的依據。

2 WOA-SVM模型

2.1 WOA

WOA是Mirjalili等[20]于2016年提出的新型群智能優化算法。該算法模擬了鯨魚捕獵時選擇包圍獵物和發出氣泡網的兩種行為,用來進行參數尋優。算法前期體現出全局搜索,后期體現出局部搜索,其具有參數量少、過程簡便的特點。假設解空間維數為D,則鯨魚個體的位置為

X=(x1,x2,…,xD)

(9)

每只鯨魚選擇包圍獵物和發出氣泡網的概率相等,都為0.5。

若選擇包圍獵物,則還分為向最優個體位置移動和向隨機個體位置移動兩種情況。

向最優個體位置移動時,位置更新公式為

X(t+1)=Xbest(t)-A·D

(10)

D=|C·Xbest(t)-X(t)|

(11)

A=2a·r-a

(12)

C=2·r

(13)

式中:Xbest(t)表示當前最優個體位置;a隨迭代過程從2線性減少到0;r為[0,1]的隨機向量。

向隨機個體位置移動時,位置更新公式為

X(t+1)=Xrand(t)-A·D

(14)

D=|C·Xrand(t)-X(t)|

(15)

式中:Xrand(t)為當前隨機個體位置。

兩種移動方式的選擇條件為:|A|<1時,向最優個體位置移動;|A|≥1時,向隨機個體位置移動。

若選擇發出氣泡網,位置更新公式為

X(t+1)=D′·ebl·cos(2πl)+X(t)

(16)

D′=|Xbest(t)-X(t)|

(17)

式中:b為定義螺旋形狀的常數;l為[-1,1]的隨機數。

2.2 基于WOA的SVM參數尋優

SVM因在小樣本分類中展現出的優良性能而被廣泛應用于工程實際中[21]。實際應用中使用的SWM一般為線性不可分SVM,通過引入核函數,將低維樣本空間映射到高維,實現樣本類型的劃分。線性不可分SVM的概念詳見文獻[22]。本文采用WOA對影響SVM性能的重要參數——懲罰因子c和核函數參數g進行優化,具體步驟如下。

(1) 初始化WOA各參數,如鯨魚個數N、最大迭代次數等;設置懲罰因子c和核參數g作為鯨魚位置向量的元素并賦初值;

(2) 將預測錯誤率作為適應度函數,因此每次迭代后最低的適應度值即為最優個體;

(3) 每個個體選擇包圍獵物或者發出氣泡網的位置移動方式;

(4) 若選擇包圍獵物,則根據|A|大小按照式(10)或式(14)更新位置并計算各適應值選出最優個體。若選擇發出氣泡網,則按照式(16)更新位置并計算各適應值選出最優個體;

(5) 重復進行步驟(3)～(4),直到達到最大迭代次數。

3 基于ST-SVD與WOA-SVM的故障診斷模型

本文所提基于ST-SVD與WOA-SVM模型的變壓器繞組松動故障診斷方法的診斷流程如圖1所示,具體步驟如下。

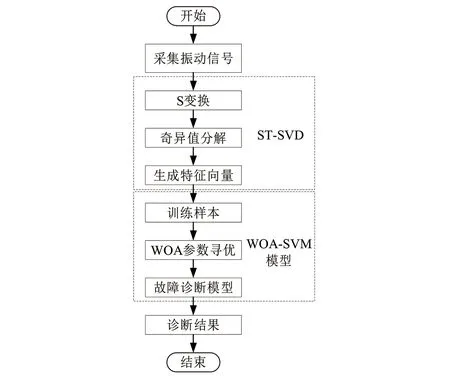
圖1 基于ST-SVD與WOA-SVM模型的變壓器繞組松動故障診斷流程圖

步驟1:在變壓器表面不同位置放置振動傳感器采集振動信號;

步驟2:將振動信號進行S變換得到的時頻矩陣轉換成幅值矩陣,再對其進行SVD得到多個奇異值;

步驟3:按照式(6)～(8)計算出特征向量,并分為訓練樣本和測試樣本;

步驟4:采用WOA優化SVM的參數c、g,以最佳參數輸入訓練樣本構建WOA-SVM故障診斷模型;

步驟5:將測試樣本輸入訓練好的模型中,輸出結果即為故障診斷結果。

4 試驗結果與分析

為驗證本文所提基于ST-SVD與WOA-SVM模型的變壓器繞組松動故障診斷方法的有效性,在試驗室環境下搭建了變壓器模擬故障試驗平臺開展試驗,如圖2所示。

圖2 變壓器模擬故障試驗平臺

由圖2可知,10 kV變壓器低壓側由調壓器將220 V電壓升高至380 V輸入,經限流電阻抑制合閘瞬間產生沖擊電流;高壓側接入容量均為30 Mvar的電容器與電抗器以模擬變壓器負載情況。由于變壓器繞組與油箱頂部相連,振動信號在變壓器頂部的采集效果更好,因此試驗時在變壓器頂部布置三個測點,測點布置圖如圖3所示。振動傳感器為IEPE型壓電式傳感器,型號為1A212E;采集儀型號為DH5922,采樣頻率設為20 kHz。

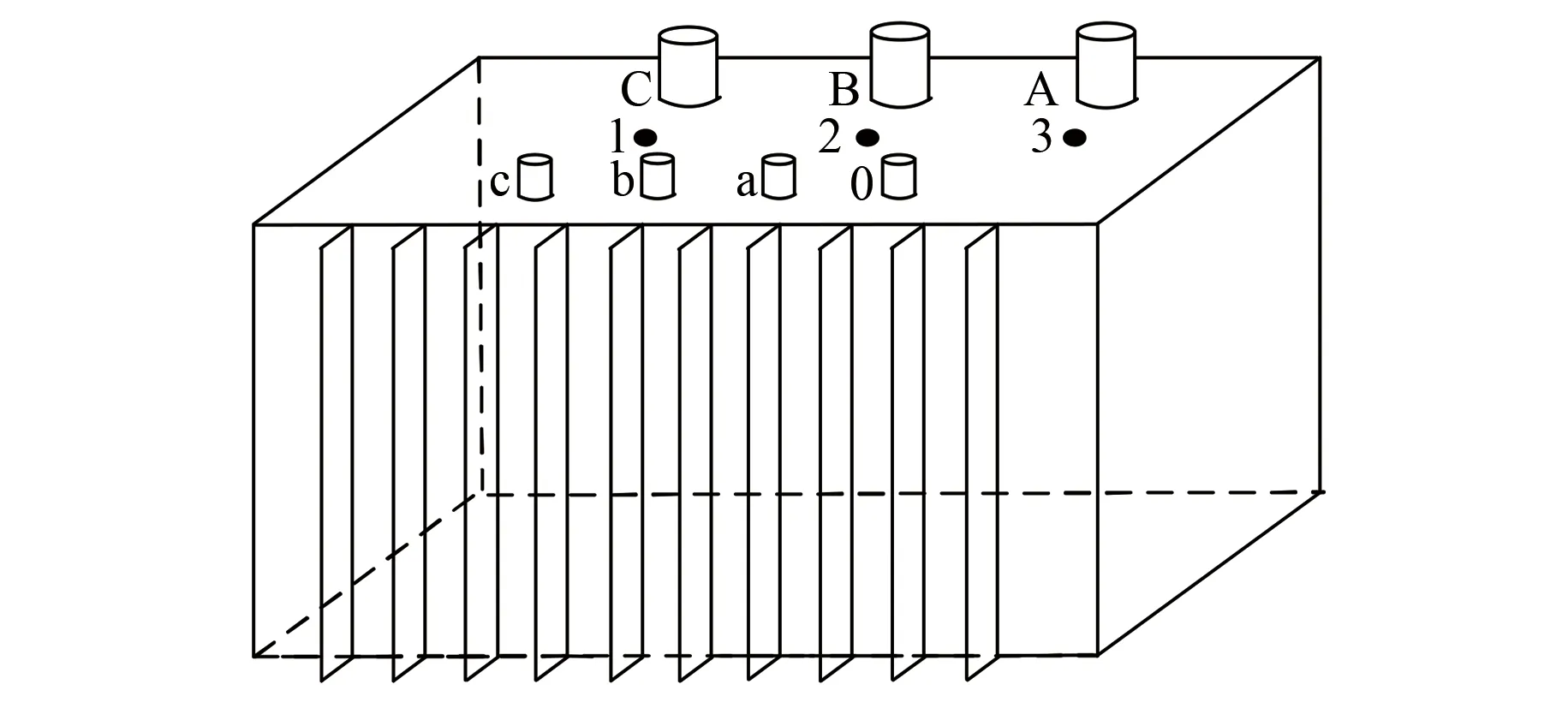
圖3 變壓器測點布置圖

故障模擬采用調節變壓器內部繞組預緊螺母松緊程度的方式。分別模擬了變壓器繞組正常、預緊力下降40%和預緊力下降80%的狀態,故障模擬圖如圖4所示。

圖4 故障模擬圖

試驗過程中對變壓器繞組處于3種狀態下的振動信號進行多次采集。以測點1為例,當變壓器繞組處于預緊力下降40%狀態下的振動信號時域圖如圖5所示。對其進行S變換后對所得時頻矩陣求取幅值矩陣,所得時頻譜圖如圖6所示。

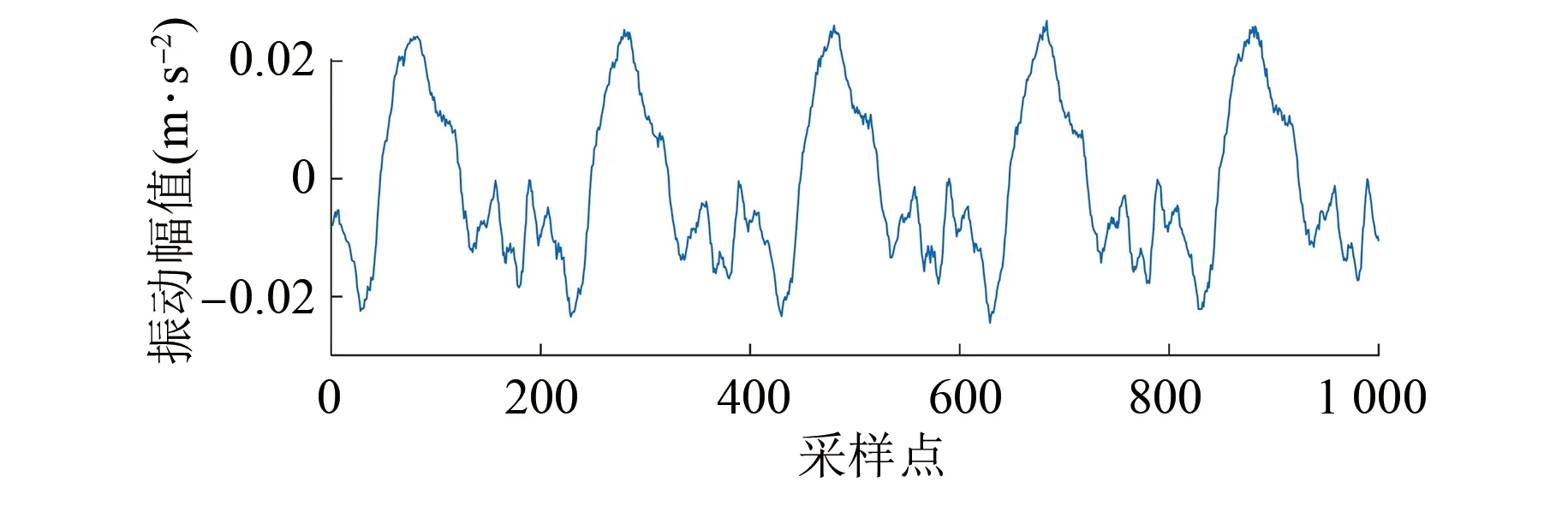
圖5 變壓器繞組處于預緊力下降40%狀態下的測點1振動信號時域圖

圖6 S變換時頻譜圖

在得到變壓器3種狀態振動信號的幅值矩陣作為特征矩陣后,對其進行SVD,所得奇異值按照式(6)～式(8)計算出相應的k1、k2、k3。表1為其中的一組計算結果。

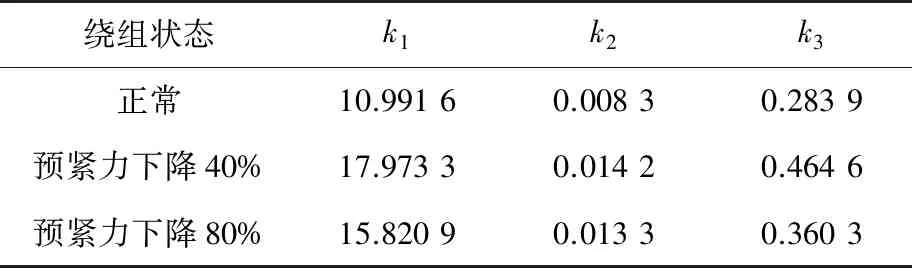
表1 特征奇異值計算結果

由表1可知,本文所提變壓器繞組處于3種狀態下的振動信號所提取的特征奇異值具有較好的區分性,表明基于ST-SVD的故障特征提取方法的有效性,也表明可通過聚類算法對3種狀態下的特征向量進行分類。

本文對每種狀態的變壓器振動信號分別提取150組特征向量作為訓練樣本,在采用WOA對SVM參數尋優時,設置c、g的取值范圍均為[0,500],最大迭代次數為50。同時,為了對比驗證本文所提方法的有效性,又構建了K-means聚類、傳統SVM和PSO-SVM模型。對每種狀態的變壓器振動信號額外提取40組特征向量作為測試樣本輸入上述模型中。各模型的診斷結果如表2～表5所示。圖7為各模型診斷結果的對比圖。

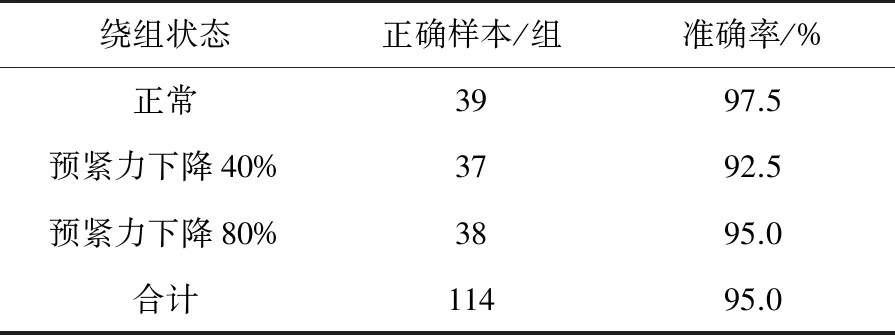
表2 WOA-SVM模型診斷結果

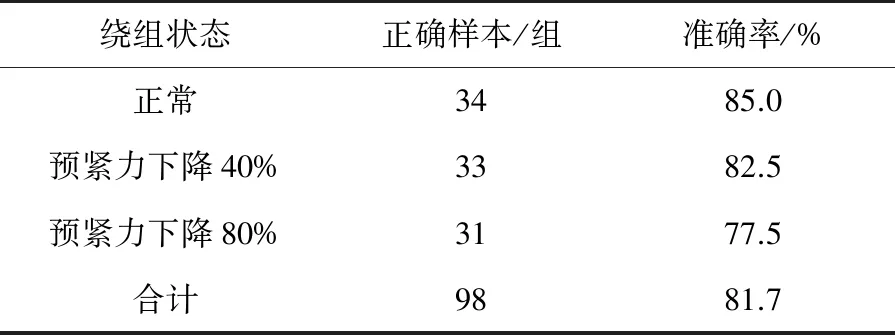
表3 K-means聚類診斷結果

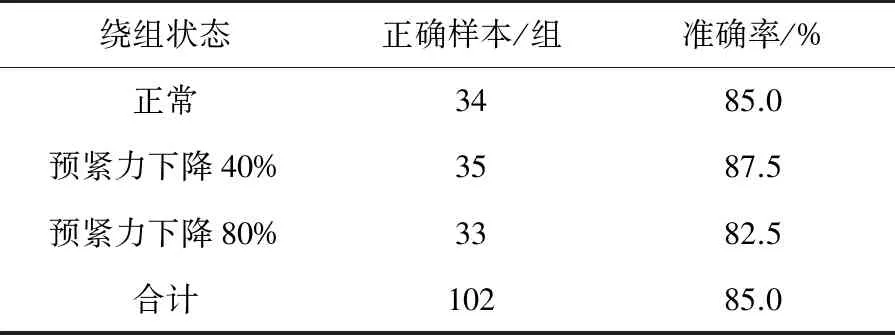
表4 傳統SVM模型診斷結果

表5 PSO-SVM模型診斷結果

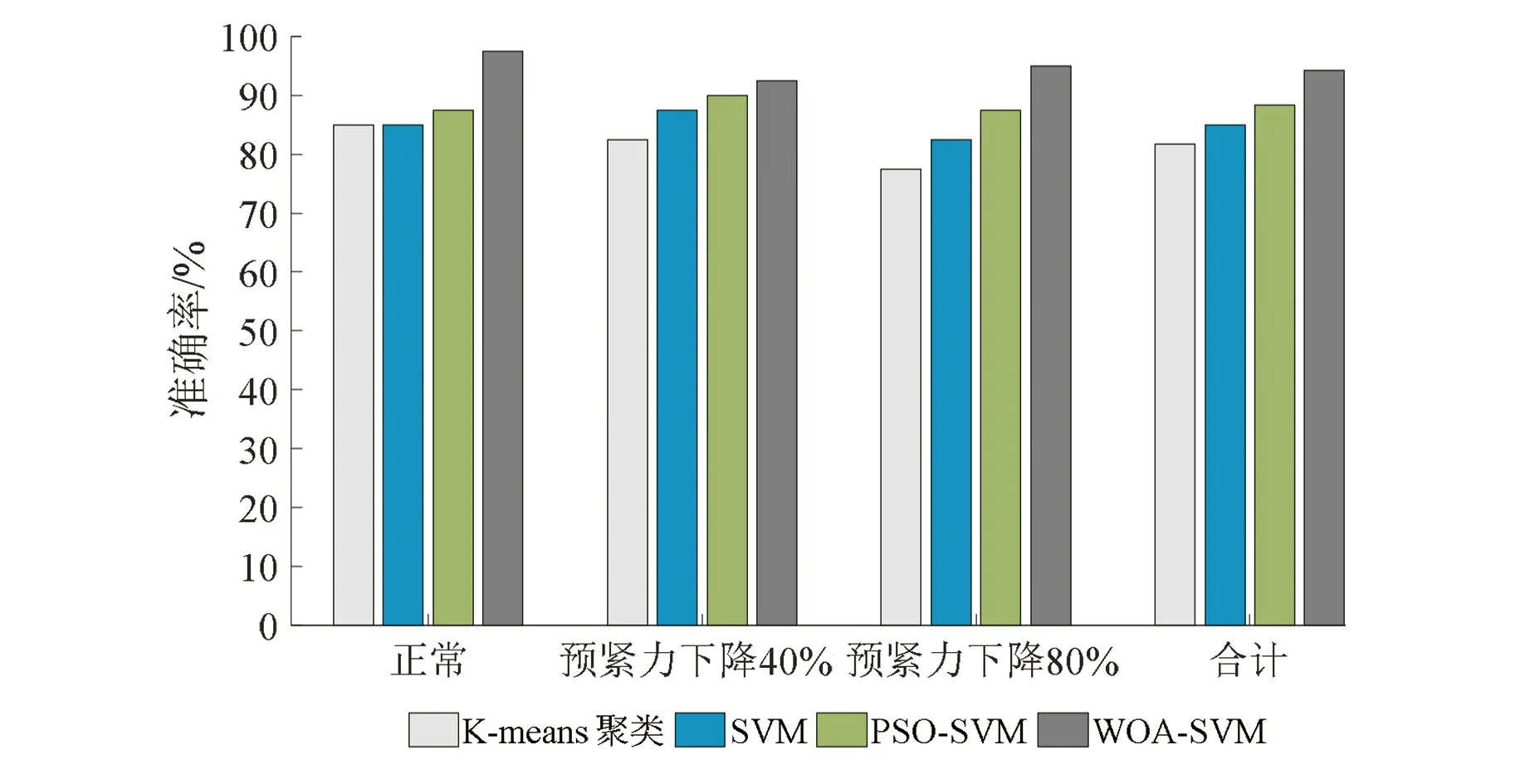
圖7 各模型診斷結果對比圖

由圖7可知,本文所提基于ST-SVD與WOA-SVM模型的變壓器繞組松動故障診斷準確率為95.0%,而在輸入特征向量相同時,K-means聚類、SVM和PSO-SVM故障診斷模型的準確率分別為81.7%、85.0%和88.3%。這表明了本文所提故障診斷方法的準確率高于傳統方法模型,適用于變壓器繞組松動故障診斷。

5 結 語

本文提出了一種基于ST-SVD與WOA-SVM模型的變壓器繞組松動故障診斷方法。通過S變換獲得變壓器振動信號的時頻矩陣,轉化為幅值矩陣后,經SVD得到多個奇異值計算出特征向量,采用WOA優化SVM的c、g參數,用上述特征提取方法提取出的訓練樣本和測試樣本分別構建WOA-SVM模型并驗證該模型的有效性,結果表明其診斷精度高于K-means聚類、SVM和PSO-SVM模型的診斷精度。