閥門類型對離心泵輸水系統停泵特性影響研究

張 醒，劉躍飛，姜 勁

（1. 施耐德電氣（中國）有限公司，江蘇 南京 210019； 2. 金陵科技學院機電工程學院，江蘇 南京 211169）

0 引 言

停泵過渡過程為泵站運行中常見的大波動過渡過程，其歷時較短且常伴隨著劇烈的壓力波動和頻繁流態轉換［1］。出口閥門在停泵開始后迅速動水關閉，起到關鍵斷流作用，同時其關閉過程中常伴隨流場的劇烈變化［2］，甚至出現漩渦、空化和水擊等威脅水泵和輸水系統運行安全的現象，因而針對停泵過渡過程中出口閥門的研究對水泵輸水系統的安全運行十分重要［3，4］。

模型試驗是研究水泵輸水系統特性的基礎［5，6］，但一方面水泵過渡過程的模型試驗難度大，成本高，部分工況具有危險性［7］；另一方面，輸水系統模型試驗的比尺選擇主要依據水泵及管道的幾何特性，很難做到模型閥門的等比例還原，若要實現閥門部件與原型相似，會大幅增加模型試驗難度［8］，已有模型試驗研究較少探究閥門偏差，以及閥門類型對停泵特性的影響。數值計算中的一維特征線法（MOC）以實驗獲得的水泵特性曲線為求解邊界條件，結合一維離散管道水錘方程求解含水泵輸水系統瞬態特性，其對閥門部件多為簡化處理，采用通用經驗模型處理閥門邊界，較難體現不同閥門特性對系統瞬態過程的影響［9］。

隨著計算流體力學（CFD）數值模擬方法的廣泛運用，水力過渡過程問題中應用CFD 方法進行數值分析愈發成熟，三維數值模擬方法不僅能直觀反映水泵內流特性，同時能體現閥門部件的流場特性［10，11］。蝶閥、球閥與閘閥是泵站出口閥門的3 種常見型式。在泵站及水電站過渡過程的數值模擬研究中，由于3 種閥門幾何結構不同且閥體運動方式有所差異，在CFD 數值模擬中采用的不同模擬方法如下：通常而言，球閥的啟閉模擬最簡便，Moujaes S F［12］等人使用STAR-CD 軟件對不同開度下的球閥進行三維CFD 模擬分析，張亞武［13］等人采用滑移網格（Moving Mesh）方法控制閥芯運動，模擬甩負荷工況下主進水閥關閥過程；蝶閥在CFD 數值模擬可以采用滑移網格的方式，Leutwyler Z［14］等人采用三維CFD 方法對蝶閥的流量、轉矩、壓力等參數進行三維模擬預測，周大慶［15］等人滑移網格法控制轉輪與蝶閥轉速的改變，完成混流泵站開機過程數值模擬；蝶閥模擬也可以采用幾何重構的動網格方法，何慶中［16］等人采用幾何重構的動網格方法對三偏心蝶閥開啟過程出現的渦街現象進行數值模擬；閘閥可采用動網格中的鋪層方法實現，夏鶴鵬［17］利用動網格的鋪層方法模擬快速閘門的啟閉。可見，針對不同的閥門類型的CFD 模擬方法有差異，在數值模擬中的難易程度也不盡相同，而已有研究較少針對不同類型閥門對系統停泵特性影響進行研究，且基于三維瞬態CFD 方法對系統中閥門類型差異的研究更少［18］。若能厘清不同閥門類型對水泵輸水系統過渡工況影響的異同點，一方面可實現CFD 數值模擬中不同閥門類型的相互替換從而使模擬過程簡化，另一方面對模型實驗中閥門部件的選擇，對改善模型試驗中閥門部件的相似性誤差具有理論指導意義。

本文構建含離心泵輸水系統的三維數值模型，基于CFD 商用軟件及動網格方法提出了含不同類型出口閥門的輸水系統停泵過渡過程數值仿真方法。分析不同出口閥型式對停泵過渡過程的水泵特性參數變化的影響及對應參數極值間的差異，結合流場內特性揭示差異形成的原因，并探究不同關閥時間對閥門間差異的影響。

1 數值計算方法及模型

1.1 基本方程

水泵輸水系統的停泵過渡過程中，工作介質為水，熱量交換較小，因而可不考慮能量方程的影響［19］，其求解的連續性方程和動量守恒方程分別為：

由于停泵工況常伴隨著壓力的劇烈波動及壓力波在輸水管道內傳播，水體的壓縮性需要考慮。結合軟件FLUENT 中用戶自定義方法（UDF），在設置水體的壓縮性時將流場內計算節點處的密度和波速表示為節點壓強的函數，體積彈性系數及波速表示為公式如下：

將初始壓強與密度值代入公式（3）得公式（5），進一步求解得節點波速與節點壓強的關系為公式（6）：

式中：p為水壓強；p0為環境壓強，取值0；ρ為水密度；a為水錘波速；ρ0為初始水密度，為1 000 kg/m3；K為水體積彈性系數，為2.2×109Pa。將公式（6）應用于管道的水錘計算時，其與實際水錘波速有輕微偏差，但本文的關注點主要為數值模擬中不同閥門型式對停泵過渡過程的影響，在同樣的參數設置下，管道水錘波速的輕微偏差可忽略。

1.2 計算模型及網格

計算模型為含離心泵輸水系統，其整體三維幾何模型如圖1 所示，模型包含離心泵，液控出口閥，壓力箱，輸水管道等部件。計算模型與原型比尺為1∶1，額定流量為13 m3/s，水泵的額定揚程為48.0 m，水泵額定轉速為300 r/min，轉動慣量為2 500 kg·m2，電機功率為9 000 kW，葉輪直徑為2.8 m，葉片數為6，葉輪中心高程為-16.3 m，閥門直徑為2.6 m，水泵前后輸水管道總長度為200 m左右。數值計算中出口閥有蝶閥，球閥，閘閥三種型式，配置不同類型閥門時僅閥門部件模型發生替換，其他部件如水泵、管道的幾何模型均相同。額定運行狀態下，水由恒定水位的上游水庫流入上游進口，經管道、水泵、出口閥門、壓力箱等部件后經下游出口進入恒定水位的高位水池。

圖1 離心泵輸水系統三維幾何模型Fig.1 3D model of water delivery system with centrifugal pump

采用結構化網格劃分管道、壓力箱、球閥和閘閥部件，對于空間扭曲較大的離心泵和蝶閥部件采用非結構化網格劃分，圖1 中展示了三種閥門的局部網格結構。通常而言，更多的網格數量對應更精確的計算結果，但增加網格數量會相應地增加數值計算的時間成本，因而在計算精度與計算速度之間尋找平衡十分必要［20］。選取網格總數為158.4 萬、259.5 萬和335.8 萬的方案1、2、3 三種網格劃分方案，3 種網格劃分方案對數值模擬結果局部略有影響，但不改變總體趨勢。在停機瞬態工況下，方案2 與3 的最大反向轉速極值相差小于1.3%，綜合考量計算精度與時間成本，選擇方案2為最終的網格劃分方式，其網格總數為259.5萬。

1.3 數值解法及邊界條件

計算采用三維CFD 商用軟件FLUENT 16.0，數值計算模型為：對流項為二階迎風格式；擴散項為中心差分格式；速度壓力的耦合方式為壓力的隱式算子分割算法（PISO）；湍流模型為Realizablek-ε湍流模型［21，22］。模型邊界條件主要為上下游進出口、葉輪轉動和閥門關閉過程，管道進口和出口采用壓力進出口邊界條件［23］，進出口剖面網格節點上的壓力值呈梯形分布，由各個節點幾何高程與水面距離換算得到，并由UDF 輸入關于節點高程的函數表達式后賦值，上游水面高程-1.3 m，下游水面高程43.7 m。葉輪轉動基于滑移網格（Moving Mesh）方法［24，25］，其控制規律通過UDF 功能控制，具體為：水泵正常運行工況下，設置葉輪的轉速n恒定為300 r/min，在2 s開始停泵后，葉輪轉速由公式（7）控制，并在每個時間步進行更新。

式中：M為停泵葉輪葉片力矩；J為轉動部件轉動慣量；dt為時間步長；dω為角速度差，ωn表示當前步角速度；ωn+1表示下一步角速度。為了簡化模型，公式（7）中省略了葉輪轉動機械摩擦力矩和發電機轉子阻力矩。

出口閥門采用直線關閉規律，額定停泵工況下閥門開度隨時間的變化規律如圖2 所示，離心泵葉輪于2 s 斷電，出口閥門同時開始關閉，經20 s 后于22 s 時完全關閉。3 種不同類型閥門的關閉過程如圖3 所示，其中蝶閥與球閥模型采用滑移網格方法控制閥體的轉動，閘閥模型采用鋪層網格方法控制閥體關閉。

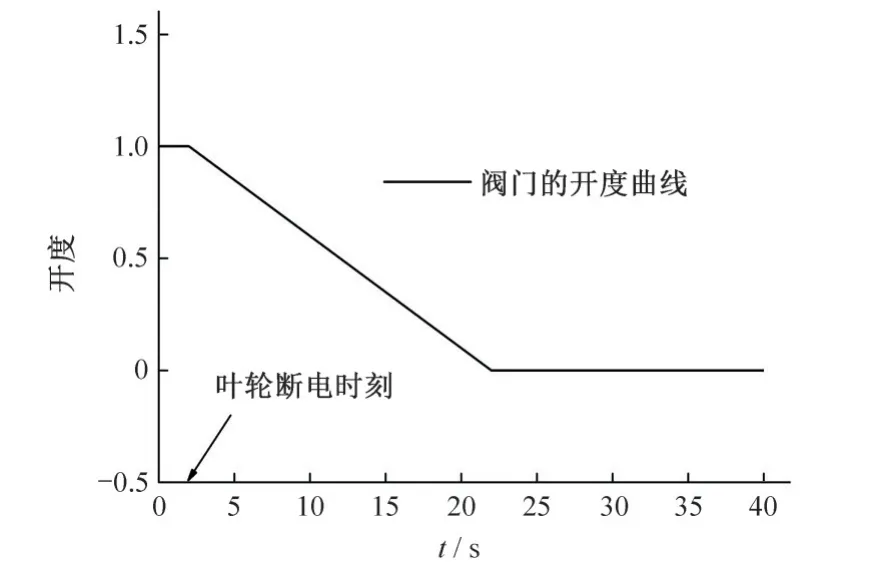
圖2 額定工況停泵時閥門與葉輪控制規律Fig.2 Control law of valve and impeller under rated stopping condition

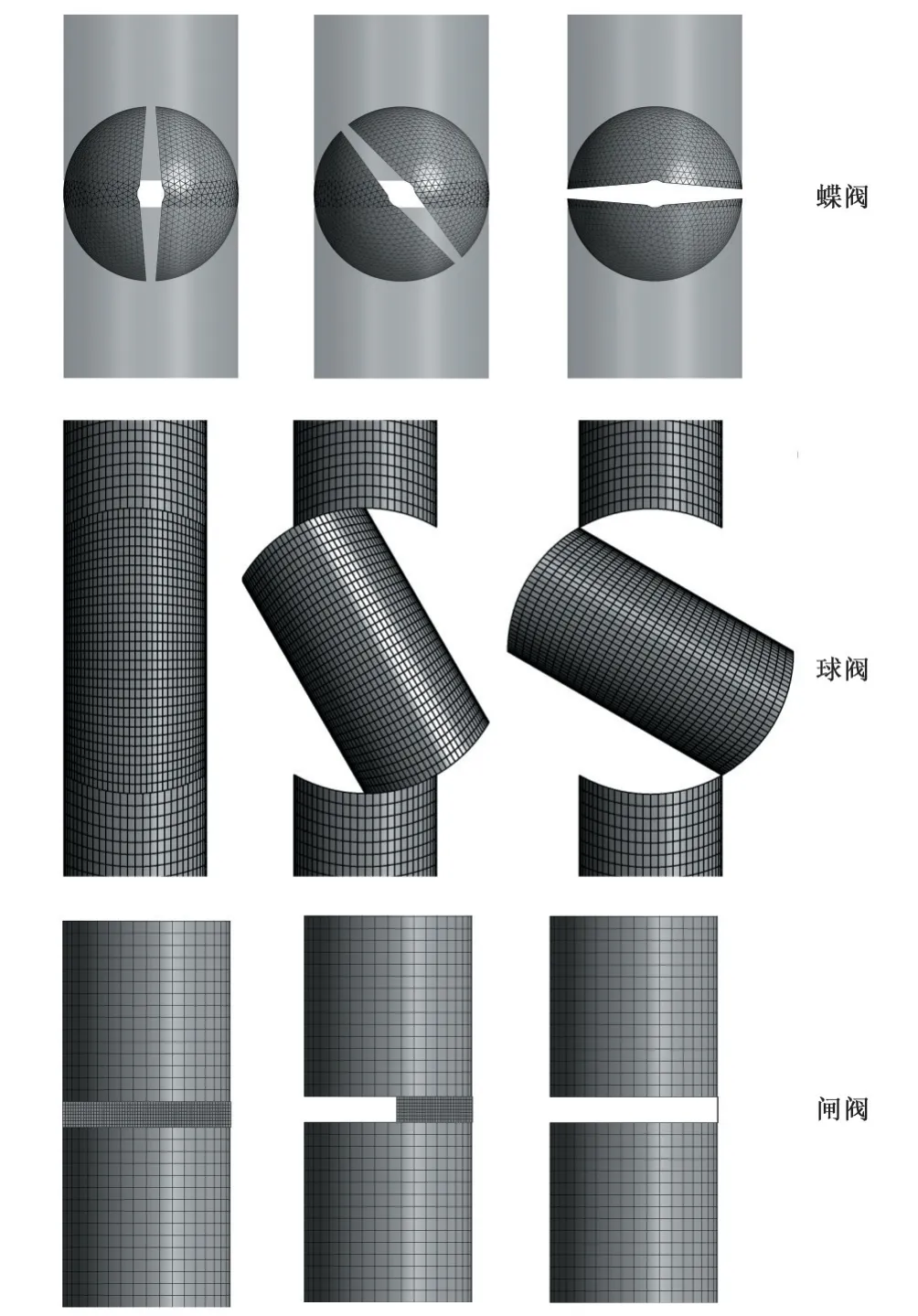
圖3 3種不同類型閥門的關閉過程Fig.3 Closing process of different types of valves

2 結果與分析

2.1 不同閥門類型對水泵外特性的影響

圖4為額定關閥時間下出口閥門類型不同時停泵過程中各參數變化圖，主要為流量Q、轉速n、揚程H與軸向水推力Fz的變化規律，其中葉片軸向力的正方向為向下。當出口閥為蝶閥時的停泵過渡過程如下：在離心泵斷電同時，出口閥門開始關閉，機組流量于4.38 s 時降為0，轉速于5.23 s 時降為0，因而停泵過程的3 個工況階段為：2～4.38 s 為停泵水泵工況，4.38～5.23 s 為停泵制動工況，5.23 s 之后為停泵水輪機工況，且各參數于22 s后逐漸趨于穩定值；在停泵水泵工況期間：水泵流量、轉速迅速下降，水泵揚程H先迅速下降，之后在0 值附近小幅振蕩；葉輪的軸向力水推力Fz于2.59 s 時達到反向最大值-20.83 kN；在停泵制動工況期間：機組流量倒流，葉輪轉速方向為正且轉速值減小；在5.23 s之后的停泵水輪機工況期間：水泵機組流量和轉速均為反向，且水泵流量與轉速的反向最大值均出現在停泵水輪機工況，反向流量于10.49 s 時達到反向最大值-12.9 m3/s，反向轉速于10.64 s時達到反向極值-327.56 r/min。

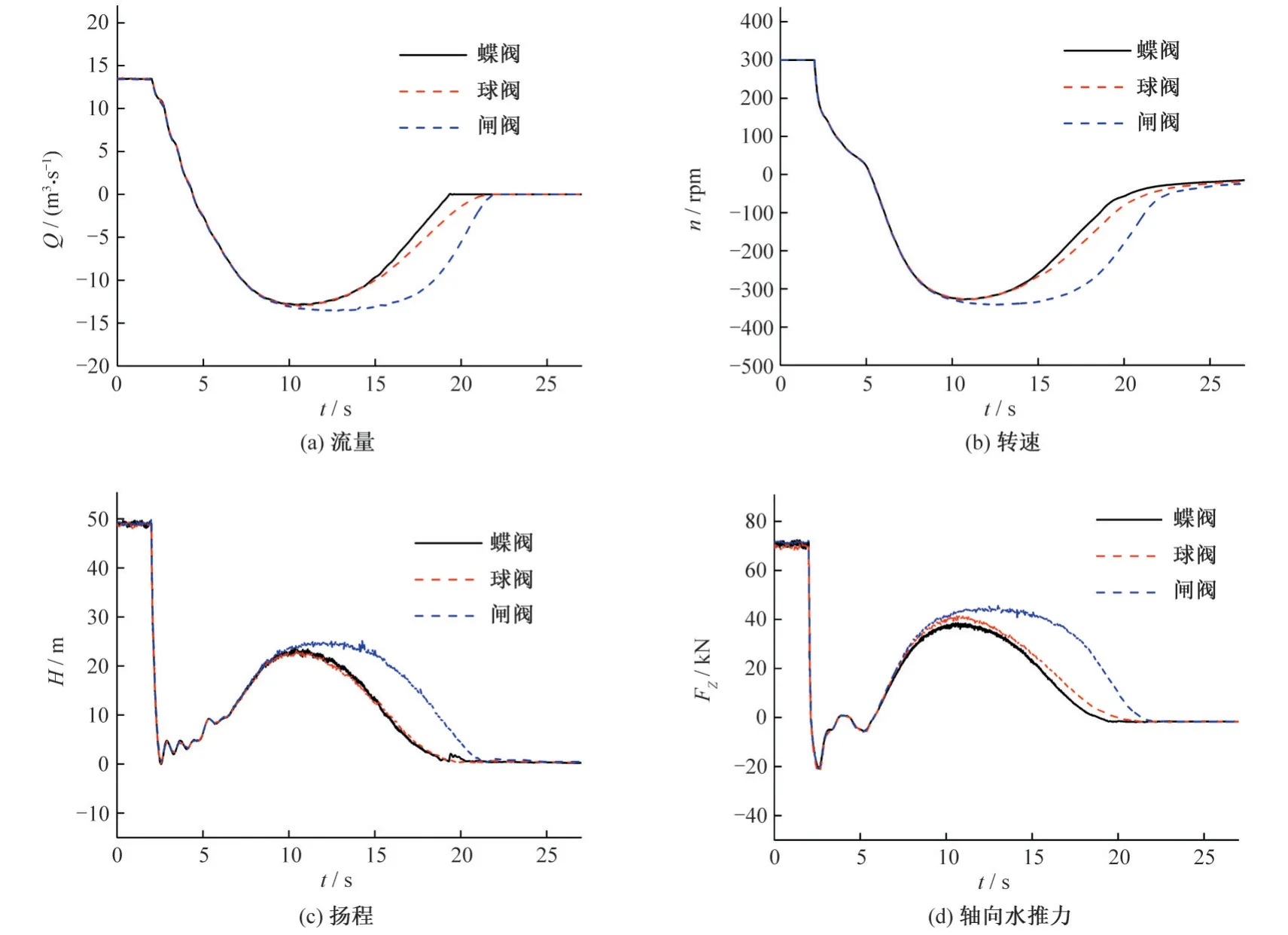
圖4 設置不同類型閥門停泵過程的參數變化Fig.4 The changing laws of parameters with different valves

水泵出口閥為球閥時，停泵過程中的參數變化曲線與蝶閥時的差異較小。此時水泵流量在4.40 s 時降為0，轉速在5.24 s時降為0，流量和轉速的變化在15 s 之前與出口閥為蝶閥時的曲線近乎重合。在15～22 s，配置球閥時的流量減小速率相較蝶閥略緩慢，原因是蝶閥閥體在關閥后期對流量有更強的截斷效應。

水泵出口閥為閘閥時，其停泵過程的前半段與前二者差別較小，而其后半段有較大差異。在停泵前半段水泵流量于4.37 s 時降為0，轉速于5.21 s 時降為0，數值與其他閥門類型近似。水泵流量、轉速、揚程與葉片軸向力變化曲線的差別主要集中在關閥的后半部分，在10～22 s 時間段內，流量及轉速的反向極值略大于出口閥為蝶閥和球閥的工況，而其反向流量與轉速的減小速率遠小于配置蝶閥與球閥時的情況，可見當出口閥門為閘閥時，在同樣的關閥控制規律下，閘閥的截流能力在三者中最小，且遠小于其余二者。

表1 為出口閥門為蝶閥、球閥和閘閥的水泵停泵過程中反向流量、反向轉速及反向軸向力的最大值，其中配置蝶閥與球閥時的反向極值數值相近，而配置閘閥時的反向極值差別明顯。由于軸向水推力在反向極值時刻處于小幅正當狀態，因而3種閥門下的軸向水推力的反向極值有小幅區別。配置閘閥對參數反向極值的影響主要體現在流量和轉速上，配置閘閥時的反向流量及反向轉速均增加，且由圖4 可知配置閘閥時發生反向流量與轉速極值的時間點均大幅延后于配置蝶閥與球閥時的工況。

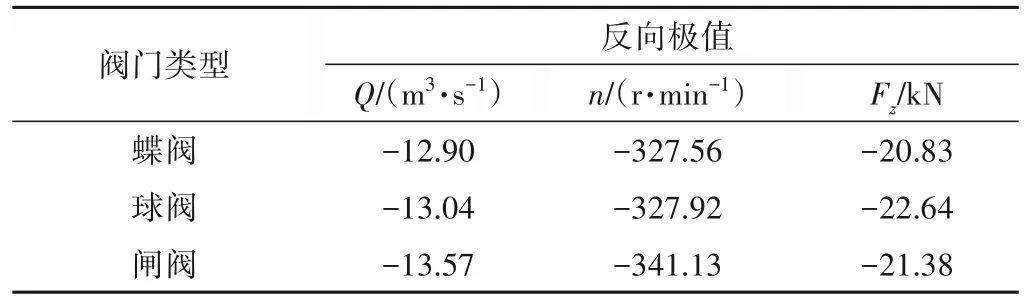
表1 停泵過程中各參數的反向極值Tab.1 Reverse extreme values of parameters

綜上可知，配置3 種不同類型出口閥門水泵按相同直線關閉規律停泵后，配置閘閥的水泵停泵特性與其他二者差異明顯，其中參數的反向極值差異主要體現在流量和轉速上，相較于蝶閥，配置閘閥時最大反向流量增加5.2%，最大反向轉速增加4.1%。

2.2 不同閥門類型對流場內特性的影響

停泵過程中，伴隨著流量與葉輪轉速的迅速變化，輸水系統內流場變化頻繁，其中更以葉輪及閥門區域為最，不同閥門類型對流場變化的影響可與外特性參數的變化規律相互印證。初始0 s時的葉輪旋轉方向為順時針，圖5為停泵過程中配置不同出口閥門時葉輪葉片壓力分布對比圖，壓力分布所在時間點均為13 s，葉片外側為壓力面，內側為吸力面。在13 s 時，各工況水泵均處于停泵水輪機工況，水流反向且反向流量較大，葉輪旋轉方向轉換至逆時針，原先葉片出口變為水流進口，水流進入葉輪區域產生的撞擊與脫流造成了13 s 時葉片上的局部高壓與負壓區域，易出現負壓空化的不利現象。當出口閥門類型不同時，其壓力分布的差異與內特性參數之間的差異規律相似，即配置蝶閥與球閥工時葉片壓力分布差異較小，而配置閘閥與前二者的差別增加，主要體現為葉片壓力面上的低壓區范圍更小，其吸力面上的高壓區范圍更大，而這與圖4中配置閘閥的揚程在13 s時更大的結果相一致。

圖5 停泵過程中葉輪葉片上的壓力分布Fig.5 Pressure distribution on blades during shutdown

由圖4 與圖5 已知在停泵過程中，水泵外特征參數變化曲線及葉片壓力分布在配置蝶閥與球閥時差異較小，因而在分析配置不同閥門類型的停泵過程閥門區域流場差異時，僅選取蝶閥與閘閥為對比對象，省略球閥。圖6 為額定停泵工況下閥門區域的壓力與速度變化對比圖，由圖2 閥門關閉控制規律可知不同類型閥門關閉時間均為2 s至22 s，圖中的方向標識為額定運行狀態下的水流流向。在停泵過程中，閥門左側水泵側的壓力呈現逐漸減小趨勢，閥門右側壓力箱側的壓力呈現先減小后增大趨勢。比較配置蝶閥與閘閥時的壓力及速度分布變化可見兩者有較大的不同：在閥門關閉過程中，蝶閥水泵側的壓力變化減小速度較閘閥更快，且蝶閥壓力箱側的壓力上升速度也更快。比較不同閥門類型對管道內流速的影響可見，在11 s時，蝶閥的上下側均出現因流道急速收縮而出現的高速區域，而閘閥管道內的高速區域在13 s 時才出現，即在相同的直線關閉規律下，由閥門處的內特性流場變化可知，蝶閥對水流的截斷效應更強，這與圖4 中參數特性變化所反映出來的規律相一致。

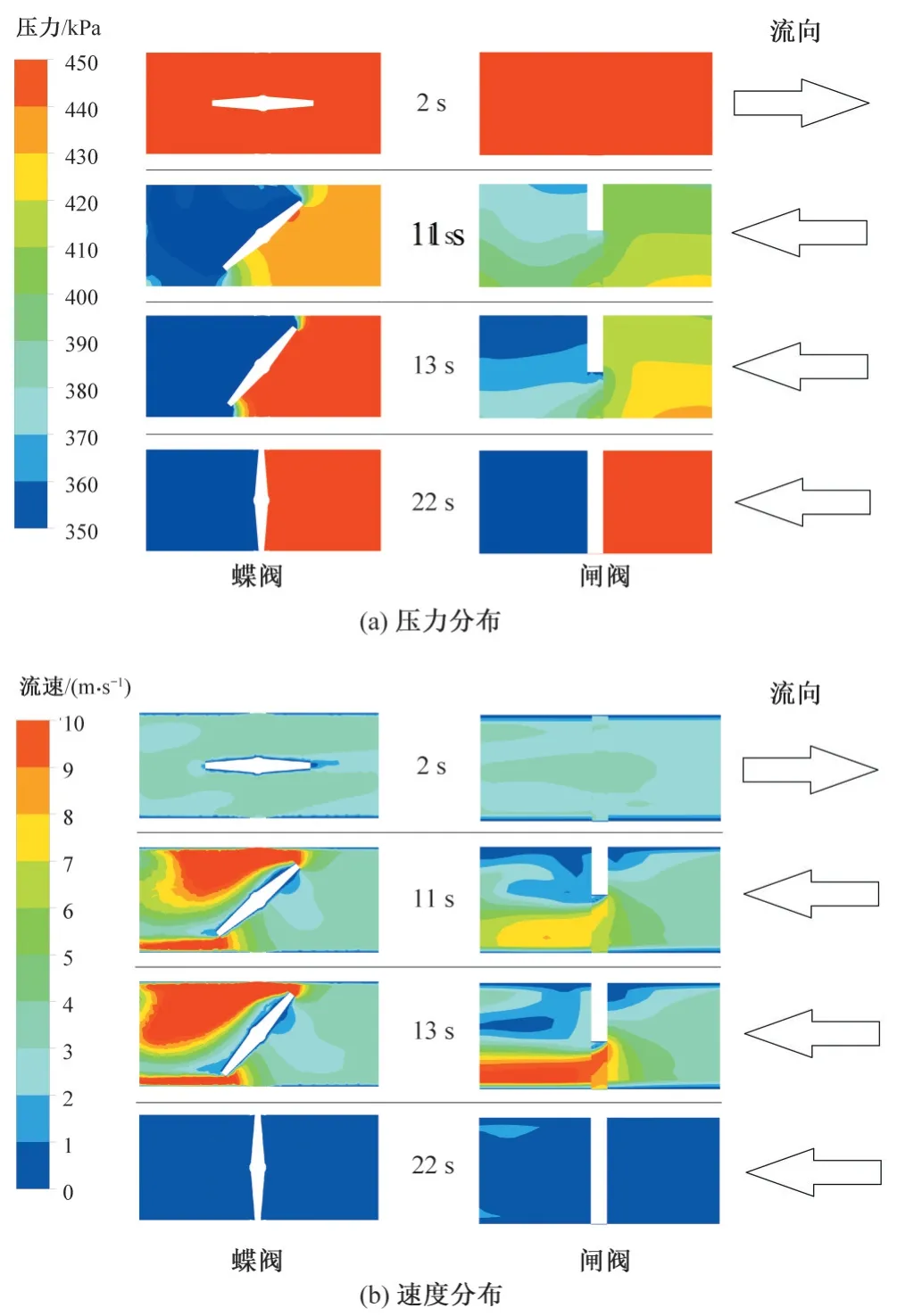
圖6 蝶閥與球閥部件處的流場變化Fig.6 Variation of flow field for butterfly valve and ball valve

2.3 縮短關閥時間對配置不同閥門時差異的影響

額定工況下的閥門控制方式為2 s 至22 s 歷時20 s 的直線關閉規律，為探究不同關閥時間下配置不同閥門時的差異，縮短直線關閥時間至5 s，此時停泵參數的變化曲線如圖7 所示。與額定20 s 停泵工況相似，當關閥時間為5 s 時，水泵內依舊有倒流現象，轉速同樣發生反轉，但是反向流量及反向轉速的極值大幅減小。對比揚程變化曲線可見，在20 s 關閥工況時，揚程曲線后段為平緩降至0，而在5 s 關閥工況時，揚程曲線后段伴有強烈振蕩。這是由于在兩種工況的關閥后段，流量均為倒流，20 s工況的關閥時間更長，流量減小時間較5 s工況更長，在5 s 的關閥工況中，倒流流量在極短時間內降為0，導致水泵出口處壓力的迅速減小及之后的壓力振蕩，同時體現為揚程曲線上的減小及振蕩。

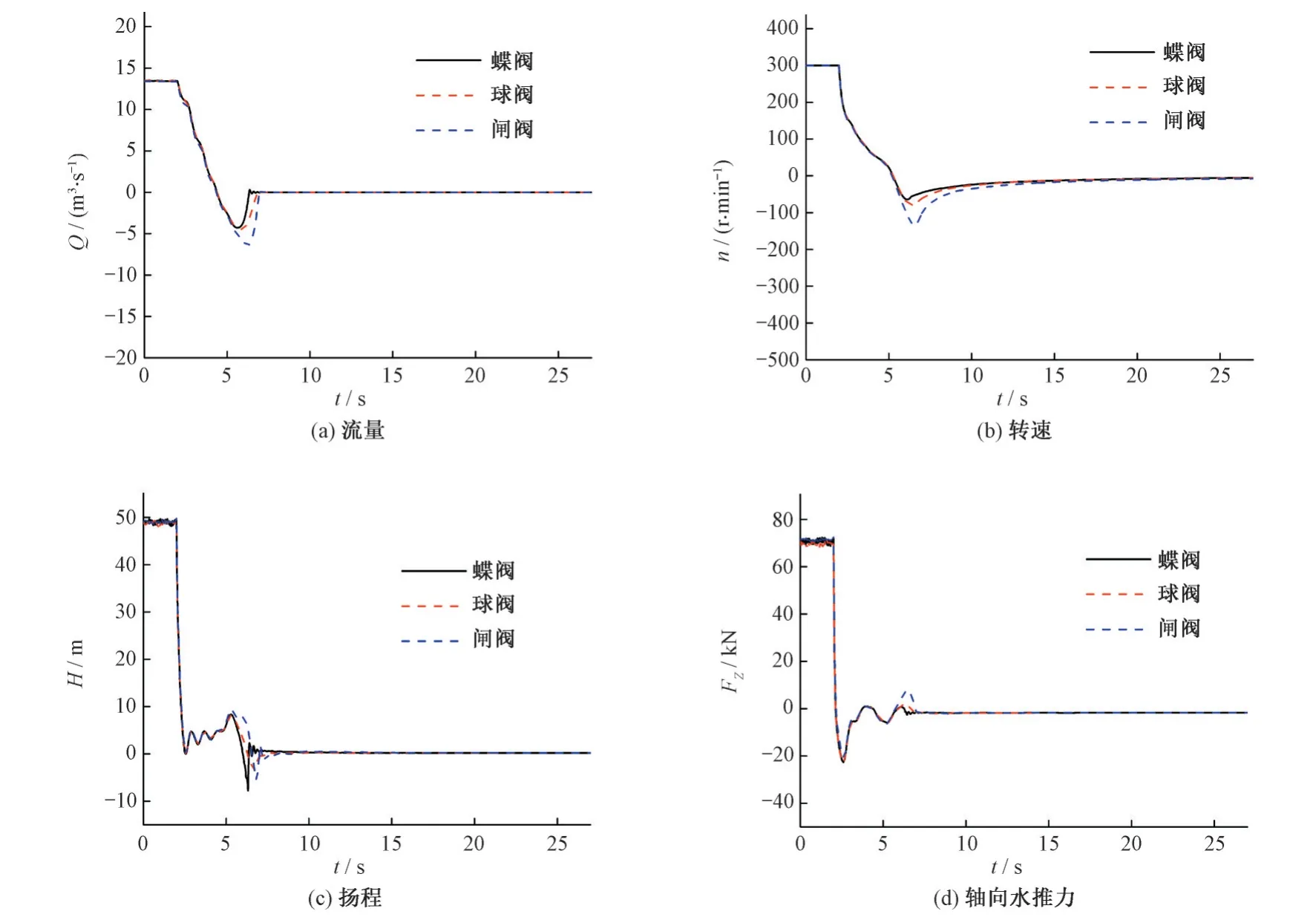
圖7 關閥時間為5 s時的停泵參數變化Fig.7 Changes of parameters when valve′s closing time is 5 s

在5 s 之前，配置不同閥門的停泵參數變化曲線是相似的，軸向水推力的反向極值發生在停泵剛開始時刻，因而配置不同閥門類型的軸向水推力反向極值在5 s 關閥時同樣差別不大。配置不同類型閥門的停泵揚程曲線變化整體是相似的，均為關閥開始時的迅速下降，及關閥末期的小幅振蕩。比較流量與轉速變化曲線，可見配置蝶閥與球閥時的停泵參數曲線較閘閥更加接近，配置閘閥的停泵參數曲線較前二者有較大差別，且其流量與轉速在倒流時段內的差別較20 s 關閥工況的差別顯著增加。

表2 為關閥時間為5 s 時，出口閥門為蝶閥、球閥和閘閥的停泵過程中反向流量、反向轉速及反向軸向力的最大值，而配置閘閥時的反向極值百分比差別顯著大于時間為20 s 的情形。配置閘閥的5 s 關閥工況下時，其流量的反向極值超出配置蝶閥工況的50%，其轉速的反向極值超出配置蝶閥工況的100%，而這兩個數值在關閥時刻為20 s時均小于10%。產生這一差異的原因是在20 s關閥時反向極值出現在關閥中間時段，而在5 s關閥時反向極值出現在關閥的末端，由章節2.1 及2.2 的分析已知閘閥與其余二閥門的差異主要集中于關閥后段，因而在5 s關閥工況中，配置閘閥停泵參數的反向極值與其余二閥門的差異增大。

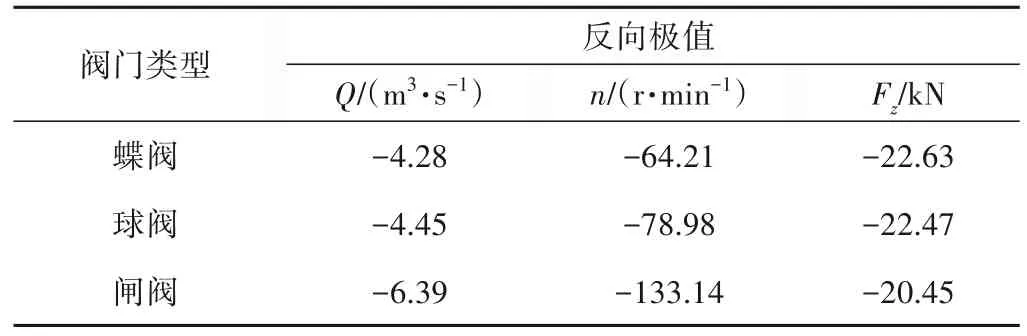
表2 關閥時間為5 s時各停泵參數的反向極值Tab.2 Reverse extreme values of parameters when valve′s closing time is 5 s

3 結 論

（1）當水泵輸水系統的出口閥門分別為蝶閥、球閥和閘閥時，配置蝶閥與球閥時的停泵參數變化規律相似，而在配置閘閥時有明顯差別，此時流量與轉速的反向極值相較于蝶閥增加5.2%與4.1%。

（2）系統停泵特性在配置閘閥與配置蝶閥、球閥時產生差異的原因為閘閥的水流截流能力更弱，比較停泵過程中不同閥門區域的內部流場特性，發現這種截流能力的差別主要體現在關閥后半段。

（3）減小閥門關閉時間后，配置閘閥時停泵流量與轉速的反向極值相較于蝶閥增加50%和100%以上，這是因為減小關閥時間使得反向極值出現的時間點移動至關閥后半段，而在此階段內閥門間過流特性差異增大。