球閥與T 型三通管組合形變件水力特性數值模擬

楊賦軍，石 喜

（蘭州交通大學土木工程學院，甘肅 蘭州 730070）

0 引 言

閥門與T形三通管組合管件在城市輸排水、農田灌溉、水力輸送等領域有著廣泛的應用。在實際水力輸送工程中為了改變水流方向，調節流量、壓力，便于水資源的高效利用，閥門常常布置在三通管支管進口，與三通管形成近距離組合形變件［1］，由于三通管與閥門中的水流特性均較為復雜，在相互影響下其水流特性與各自獨立時有較大的不同，因而阻力損失也會發生較大變化，有必要對組合形變件進行水力特性分析。

國內外學者采用試驗與數值模擬方法對三叉管、閥門的水力特性進行了大量的研究。WEN 等［2］對球閥關閉過程進行了分析，對不同開孔條件下的水流流動進行了計算，所得到的水頭系數與試驗結果吻合較好。KOLESNIKOV 和NIKIFOROV［3］在壓力管道設計對進口球閥運行的影響中提到，球面閥用于高水頭渦輪裝置時，為其提供均勻的供水，不會出現旋轉、連續性破裂。GAN 和RIFFAT［4］利用CFD 技術對T 形管內水流的流動進行了數值模擬研究，分析了流速及流場的變化。楊校禮等［5］通過數值模擬的方法對抽水蓄能電站分岔管的水力特性進行了分析。石喜等［6］對DN75×75PVC三通管進行試驗和數值模擬研究，表明引起局部阻力系數的主要原因是在較大分流比時水流的剪切和橫向環流導致直管分岔處上側的漩渦運動和流速梯度變化損失。陳江林等［7］探討了T 型三通管的流動特性，分析了不同工況下水頭損失的產生機理，結果表明，數值模擬結果與試驗結果吻合較好。陳偉業［8］研究了T型三通管的局部水頭損失，表明在分流比為0.4～0.6 附近變化時，兩支管內流速相近，產生的漩渦相互影響較小，數值模擬的結果與試驗結果基本吻合。韓圓圓［9］對T形三通側支管內氣液兩相流進行數值模擬和試驗研究，結果表明隨著T型三通管內流體的分流比降低，側支管入口漩渦尺度逐漸減小，局部阻力損失與分流比有著密切的聯系。

以上主要研究三通管或直流管道與閥門組合的單向流以及多相流的阻力損失、分流比不同時的阻力特性以及水流在通過球閥時發生的水錘渦流等，對三通與閥門的組合形變件水力特性研究很少，石喜等［10］利用Fluent 軟件對直流管道與球閥的組合管件進行了固液兩相流數值模擬，探討了球閥的流場特性、顆粒分布特征以及壓力損失的變化規律。本文在前人研究的基礎上，采用數值模擬的方法對球閥與T 形三通管組合形變件的水力特性進行研究，分析閥門開度、雷諾數、分流比三者變化條件下，球閥與T形三通管組合形變件的水力特性，同時探討了綜合阻力系數和流場的變化，以期為管網供水和水力輸送提供參考。

1 計算模型與方法

1.1 基本方程

描述不可壓縮流體的基本方程可由連續性方程、N～S 方程等構成，對于管道中的水流，流經閥門與T形三通管組合管件時連續不可壓縮，其連續性方程為［11］：

式中：ux、uy、uz分別為流體質點速度在x、y、z方向上的分量。

N～S方程為：

式中：ρ為流體密度；vx、vy、vz分別為流體在x、y、z方向的速度分量；τ為黏性動量通量；μ為流體動力黏度；p為壓強；gx、gy、gz分別為重力在x、y、z方向的分量；

1.2 湍流模型與計算方法

在Fluent 進行數值模擬時，為了試驗數據與模擬數據有更高程度的吻合，方程采用二階迎風格式離散，速度與壓力耦合計算采用SIMPLEC 算法［6］，方程的離散采用有限體積法，擴散項采用中心差分格式，選用k-ε模型中的Realizablek-ε模型，該模擬在模擬水體回流和旋轉以及計算壓力梯度、射流擴散率時有較高的精度［12］。湍動能及耗散率運輸方程如下［13］：

式中：ρ為流體密度；t為時間；k為湍動能；ε為耗散率；μ為流體動力黏度；xi、xj為坐標分量；εijk為三階單位張量；σk為湍動能k的湍流普朗特數（取1.0）；μt為湍流黏性系數；σε為耗散率ε的湍流普朗特數（取1.2）；Gk為平均速度梯度引起的湍動能產生項；Gb為浮力影響引起的湍動能產生項；YM為可壓縮湍流的擴張消散項；ui、uj為速度分量；為角速度；C3ε為與浮力項有關的系數；ωk為參考系中觀察的時均轉動速度張量；Sjk、Ski為應變率；C1ε、C2、A0為常數，分別取1.44、1.9、4.04。

2 幾何模型與計算方法

2.1 實際工程應用

在管網輸水、農田灌溉過程中，T形管與閥門組合形變件得到廣泛應用，為改變水流方向、調節流量、便捷輸水、提高水資源利用率、節約管材等提供了很大幫助。

圖1 T形管與球閥組合形變件工程應用示例Fig.1 Engineering application example of T-shaped pipe and ball valve combined deformation parts

2.2 幾何模型

本文選用DN63PVC 球閥與T 形管件組合，閥門啟閉件3 是帶孔球體，與閥桿和手柄連接，通過繞垂直軸線轉動手柄來啟閉閥門，T 形管采用DN63PVC 管道，球體內徑通道為57 mm，球閥結構圖如圖2所示。

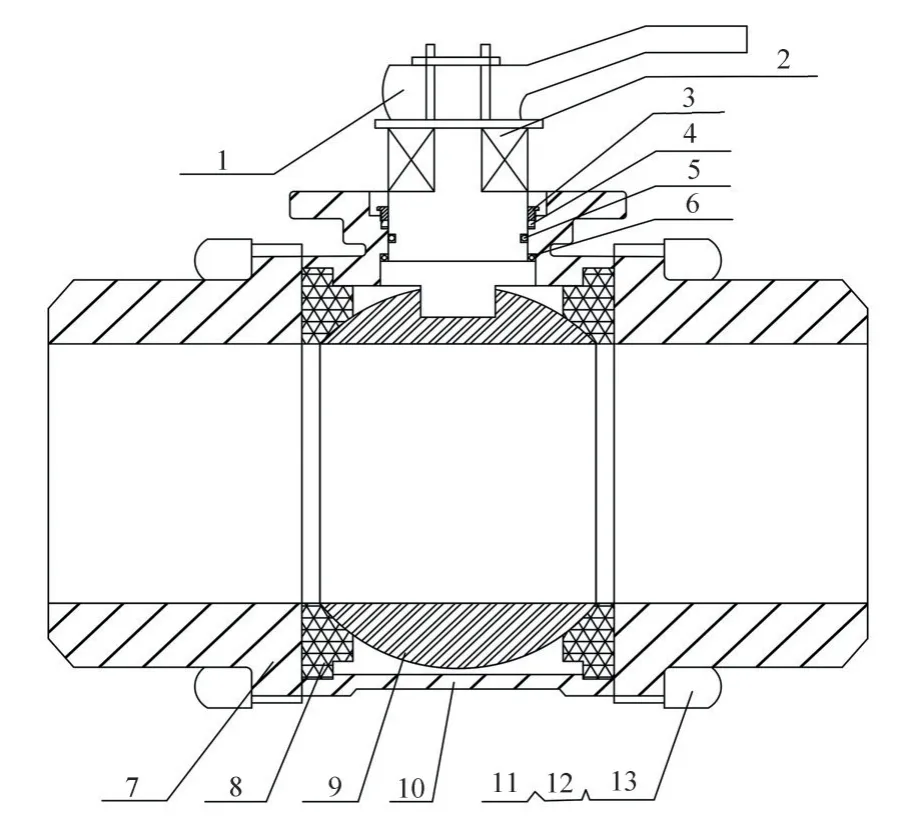
圖2 PVC球閥結構示意圖Fig.2 Structure diagram of PVC ball valve

圖3為T形管與球閥組合平面圖，坐標原點取T形管主管與支管中心軸線交點，水流方向取X軸正方向。為了減小計算區域的影響，計算尺寸取大于管徑10倍［14］，支管連接球閥，以球閥的閥門開度為60°為例。上游和下游的連接管道均為DN63PVC管，內徑為57 mm，管道放置水平，不同分流比q=Q1/Q、（Q為主管流量，Q1為側管流量，Q2為支管流量）進行數值模擬。Fluent計算模型幾何區域取上游長度為L1=826.5 mm（L1＞10d，d為管道公稱直徑），側管下游長度L2=950 mm（L2＞15d），球閥下游長度L3=950 mm（L3＞15d），為了保證計算準確性，取壓點為取上游10d處，下游15d處的位置，設置進口穩定流速為3 m/s，水體溫度為20 ℃，密度為ρ=998.2 kg/m3，運動黏滯系數υ=1.006 7×10-6m2/s，取Z軸負方向為重力方向。

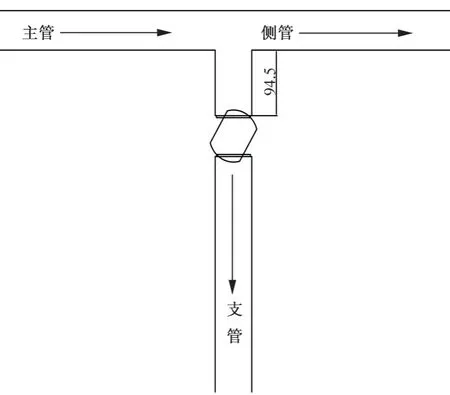
圖3 管道中水流方向Fig.3 Direction of flow in the pipe

2.3 網格劃分及網格無關性驗證

采用AutoCAD 軟件對T 形三通管與球形閥門組合形變件進行建模及組合，利用Gambit軟件對所建模型進行網格劃分以及邊界條件設置，球閥位置及交叉處采用四面體網格和混合網格劃分進行加密，其余部分均采用六面體結構網格劃分，網格劃分如圖4所示。

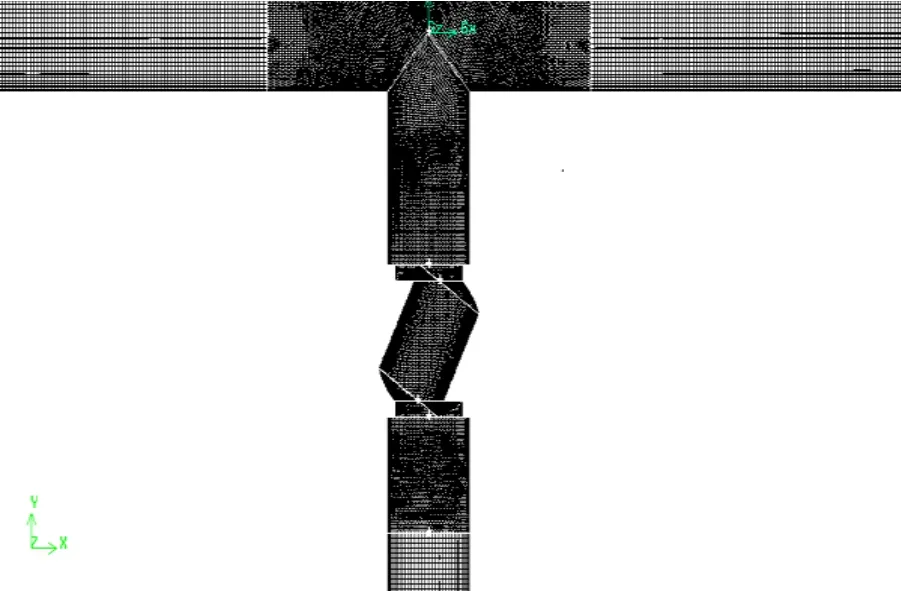
圖4 網格劃分Fig.4 Mesh generation

為了確保網格數量對數值模擬計算結果的影響最小，需進行網格的無關性驗證。以水流進口速度為3 m/s，球閥閥門開度以60°為例，球閥與主管的間距為94.5 mm時的阻力系數為指標進行無關性驗證，結果如圖5 所示。當組合形變件計算區域的網格數量大于60 萬時，綜合局部損失變化將趨于穩定，為保證計算的精度，本文的計算區域網格數量取81萬～83萬個。

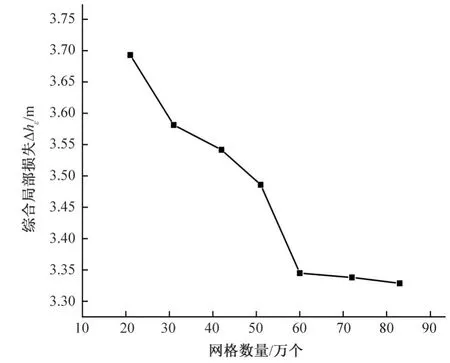
圖5 網格的無關性驗證Fig.5 Verification of grid independence

邊界條件設置：主管進口斷面與水流方向垂直，設置一定的流速，給定湍流強度和水力直徑，支管出口和側管出口均為自由出流邊界條件，管壁及閥門內壁均采用無滑移邊界條件，對于靠近邊壁區流動的計算采用標準壁面函數［15，16］進行處理，壁面粗糙高度設為0.001 5 mm，湍流強度的計算公式為［6］

式中：ReD為按水力直徑計算的雷諾數；υ為運動黏滯系數，m2/s；v為水流進口流速，m/s；D為管道直徑，mm。

3 結果與分析

3.1 綜合阻力損失與系數計算

根據伯努利方程［17］，主管—支管、主管—側管的計算區域斷面間能量守恒，綜合局部損失根據以下公式進行計算：

式中：Z0、Z1、Z2為主管進口、側管出口、支管出口的位置水頭；p0、p1、p2為主管進口、側管出口、支管出口的壓強；υ0、υ1、υ2為進口流速，側管出口、支管出口流速；α0、α1、α2為動能修正系數（取1.0）；ρ為流體密度；g為重力加速度（取9.81 N/kg）；Σhw0-1為主管～側管的綜合阻力損失；Σhw0-2為主管～支管的綜合阻力損失；ζ01、ζ02為主管～側管、主管～支管綜合阻力損失系數

在進行水力計算時，根據能量方程計算出組合形變件上下游計算部分的水頭損失［18］ΔhΣ，再計算出綜合局部阻力損失Δhζ，最終計算得出綜合局部阻力損失系數［19］ζ。實際上綜合局部阻力系數不是一個定值，它跟閥門開口度大小、分流比、雷諾數、形變量、管道光滑程度等因素有直接關系，即ζ=f(θ，q，Re，ε，φ)特別是在短管以及管件組合形變處，局部阻力損失相對于沿程阻力損失占的比重相對較大，若按照固定的局部阻力系數或與沿程水頭損失一定的比例進行局部水頭損失的計算，結果會導致水力計算不準確。

3.2 組合形變件水力特性分析

為了探究球閥與T 形三通管組合形變件水力特性規律，本文采用Fluent對這種特殊組合形變件在水平放置時進行數值模擬。根據圖6（a）可知，當流速為3 m/s，閥門開度為30°時，閥門進、出口流速的變化極大，閥門上下游出現大面積的回流、旋渦，閥芯內也形成了旋渦，水流能量損失較大，流線分布也比較紊亂；隨著閥門開度為45°［圖6（b）］時，流速梯度有明顯降低，尤其是閥芯上下游位置，閥門上下游回流面積、渦流量也相對減少，流線分布逐漸均勻；當閥門開度為60°［圖6（d）］、70°［圖6（e）］、90°［圖6（f）］時，明顯看出閥門附近流速變化不大，旋渦面積趨于穩定狀態，流線分布相對較穩定。當閥門開度大于70°時，流速變化穩定，因此，閥門開度的大小對組合形變件的能量損失有著密切的關系。

為探究組合形變件在不同工況下的水力特性，其他條件不變只改變進口流速，取特殊角度進行對比分析。由圖7可知，當進口流速為2 m/s，分流比不變，閥門開度分別為30°［圖7（a）］、45°［圖7（b）］、60°［圖7（c）］時的流速流線圖，與圖6（a）、圖6（b）、圖6（d）進行對比，明顯可以看出，當流速變化為2 m/s 時，閥門處的最大流速降低非常明顯，流線的分布也相對均勻，閥芯及閥門前后的渦流面積降低，流體進入支管時對拐角處的碰撞密度下降，由此可以看出，當閥門開度和分流比不變的條件下，流速大小對綜合阻力損失也有著很大的影響。

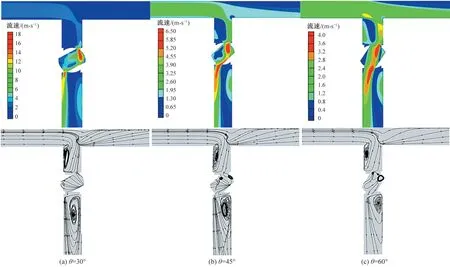
圖7 流速（ν0=2 m/s）云圖及流線分布Fig.7 Velocity and streamline distribution

如圖8 所示，當流速為3 m/s 時，閥門開度在特殊角30°、45°、60°時組合形變處流場變化情況。可以明顯看出閥門附近及閥芯內部的流場的分布非常密集，在水流流經管道分叉處及閥門時，部分區域出現回流、渦流及對管壁的碰撞，組合形變件對水流方向的改變，使得管道內水流出現旋渦，造成水流能量的損失。

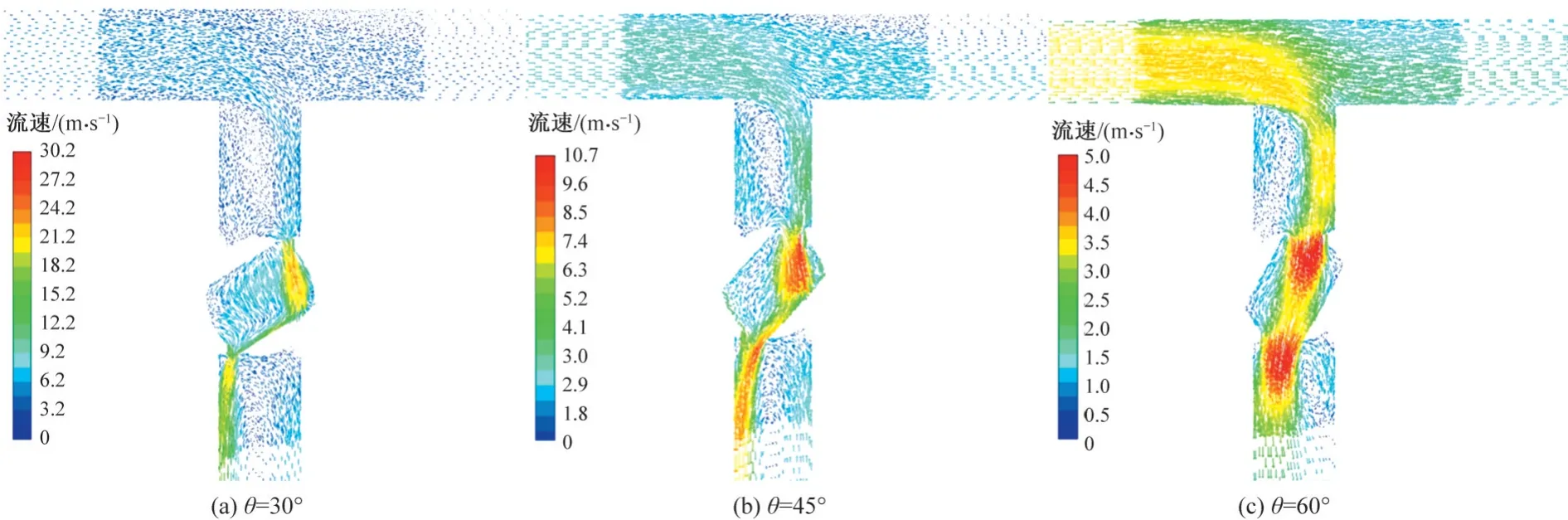
圖8 流場分布圖Fig.8 Flow field distribution diagram

3.3 綜合阻力系數的變化

3.3.1 綜合阻力系數隨閥門開度的變化

當進口流速分別為1.5、2、2.5、3、3.5 m/s，分流比為0.5 時，根據（9）～（12）計算出綜合局部阻力系數如圖9所示。

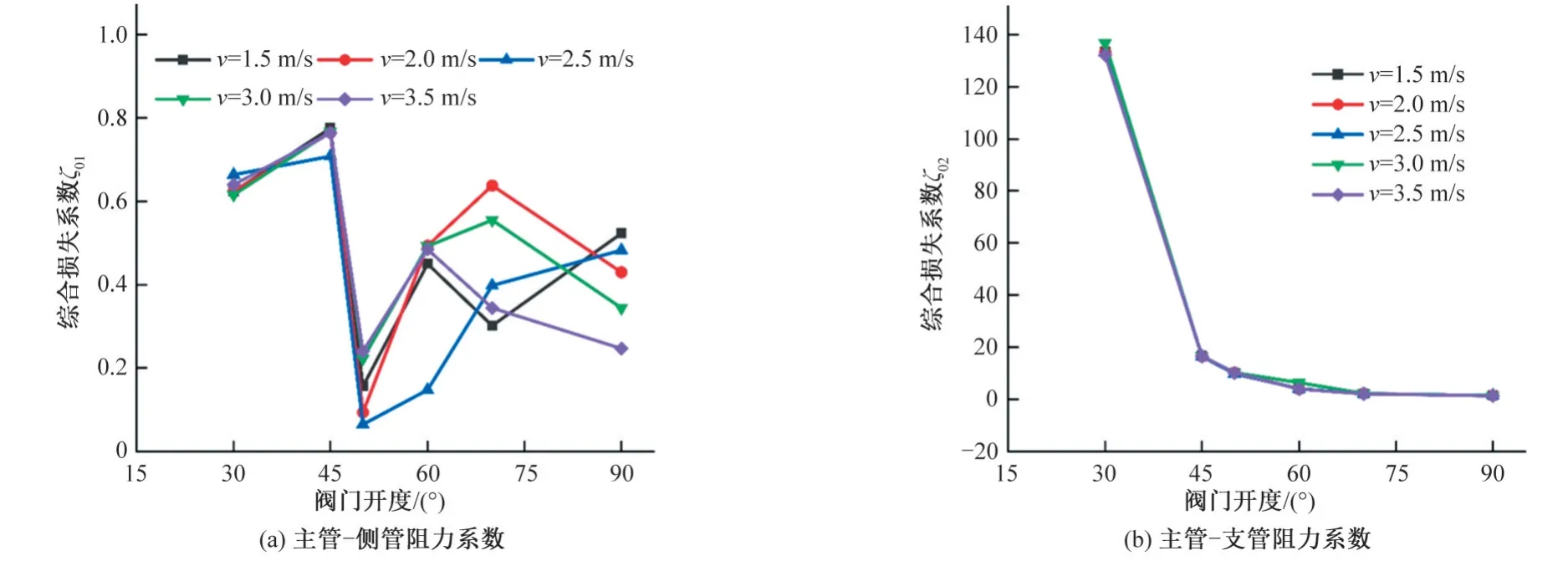
圖9 損失系數隨閥門開度的變化Fig.9 Change of loss coefficient with valve opening

由圖9可以看出：在不同進口流速的條件下，主管—側管的綜合損失系數ζ01、主管—支管的綜合損失系數ζ02都隨著閥門開度變化；主管—側管損失系數隨閥門開度呈現上下波動狀態，但是當閥門開度大于70°時，損失系數變化幅度基本趨于穩定狀態，主管—支管損失系數隨著閥門開度增大一直減小，直到閥門開度大于70°時系數趨于穩定。閥門開度從30°～45°變化時，損失系數呈斷崖式下降，這是因為隨著閥門開度的增大，閥門的過水能力增大，管道水流在形變處的渦流量迅速減少，水流與管道碰撞所產生的能量損失也隨之減少；當閥門開度大于45°時，過水能力的增大引起損失系數變化率逐漸減小。因此，在T形管與球閥組合形變件的管道中，閥門開度對于損失系數的影響至關重要。

3.3.2 綜合阻力系數隨Re的變化

圖10 所示為主管—側管的綜合損失系數ζ01、主管—支管的綜合損失系數ζ02隨雷諾數的變化情況。由圖10（a）可知，隨著雷諾數的不斷增大，主管—側管的損失系數呈現波動狀態且逐漸減小。由圖10（b）、（c）可知，主管—支管的綜合損失系數隨著雷諾數的增大而減小。因此，綜合損失系數隨著雷諾數的增大而減小。

圖10 損失系數隨Re的變化Fig.10 Variation of loss coefficient with Reynolds number

3.3.3 綜合阻力系數隨分流比的變化

當流速為3 m/s，分流比分別為0.4、0.5、0.6 時，損失系數變化如圖11所示。

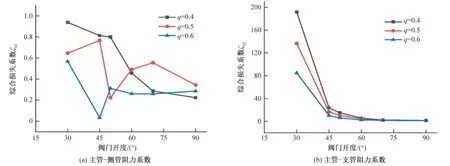
圖11 損失系數在不同分流比的變化Fig.11 Variation of loss coefficient at different split ratios

由圖11 可知：在不同分流比的條件下，球閥與T 形管組合形變件損失系數的變化情況，當球閥開度一定時，主管—側管損失系數隨著分流比的增大而出現小范圍的波動，當閥門開度大于70°時，損失系數逐漸降低并趨于緩和。主管—支管損失系數隨著分流比的增大而減小；且隨著閥門開度的不斷增大，過水能力的增強，損失系數逐漸減小趨于穩定。

4 結 論

（1）綜合阻力損失系數的大小取決于閥門的開度大小，閥門開度為30°時，閥門前后形成大面積的渦流，閥門進口速度急劇增大，造成猛烈撞擊水頭損失較多；當閥門開度增大至45°時，隨著過水能力的增強，流速梯度下降明顯，渦流量及渦流面積減少，損失系數呈現斷崖式下降；閥門開度大于70°時，渦流面積量及損失系數逐漸趨于平穩，由此可見，組合管件損失系數在閥門開度大于70°時基本保持不變。

（2）當組合形變件的分流比和閥門開度一定時，主管—側管損失系數隨雷諾數的增大出現范圍波動，總體趨勢減小，主管—支管損失系數隨雷諾數的增大而減小，在雷諾數大于1.8×105之后，綜合阻力損失系數基本保持穩定，可認為水流此時進入阻力平方區。

（3）根據數值模擬結果進行分析，得到組合形變件內分流比的不同也是影響損失的關鍵因素，當流速一定時，在不同分流比的條件下，損失系數隨著分流比的增大而減小。