四輪驅動拖拉機牽引性能預測模型建立與試驗
趙靜慧 劉孟楠 徐立友 于 碩 謝普康
(1.河南科技大學車輛與交通工程學院,洛陽 471003; 2.洛陽拖拉機研究所有限公司,洛陽 471003;3.智能農業動力裝備全國重點實驗室,洛陽 471039)
0 引言
牽引性能是拖拉機將使用重力轉換為對農機具有效牽引力的能力,決定了耕整和運輸作業過程中的整機效率和技術經濟性,是拖拉機最重要的使用性能之一[1-2]。拖拉機牽引性能通常由牽引效率、滑轉效率、最大牽引力等指標評價[3],其中,驅動輪滑轉率同時影響整機牽引效率和最大牽引力,是拖拉機牽引性能的主要影響因素。然而,滑轉效率受輪胎、土壤、超前率、載荷波動等復雜因素共同影響,計算分析過程非線性強[4-6]。因此,從輪胎-土壤附著特性入手揭示滑轉效率影響機理,提出基于模型的田間牽引性能預測方法是優化拖拉機總體參數與設計方案的重要科學問題,對于改善農業動力裝備綜合使用性能具有重要意義。
拖拉機田間牽引性能預測方法一直是國外農業動力裝備領域研究的熱點[7-8],FERVERS[9]提出了采用有限元方法對土壤-輪胎接觸面幾何形狀以及土壤正壓力和剪切力分布建模的方法;文獻[10-11]提出了基于貫入試驗和概率分析的半經驗方法,建立了拖拉機行走系在均質土壤中的載荷-沉陷關系和剪切應力-位移關系模型,用于計算整機附著性能;GUY[12]分析了前后軸交互作用對四輪驅動拖拉機牽引效率的影響機理,并開展了田間試驗驗證;WONG等[13-14]以四輪驅動拖拉機滑轉效率最優為目標,分析了前后不協調系數對底盤牽引附著性能的影響機理。國內相關研究較少,張文春等[15-16]基于小功率后輪驅動拖拉機牽引試驗數據建立了滑轉效率計算經驗模型;徐挺[17]建立了四輪驅動拖拉機前后不協調系數優化計算模型。相關研究為四輪驅動拖拉機田間牽引性能預測提供了理論基礎,但是均未能充分定量地分析前后輪附著差異、載荷轉移和前后運動不協調因素對滑轉效率和牽引性能的影響,影響了模型預測的準確性。
本文從拖拉機單個輪胎的驅動特性和載荷特性分析入手,通過引入輪胎指數、機動指數,充分考慮牽引作業過程中的土壤條件、前后橋運動不協調、質心位置轉移、前后輪附著特性差異等多變量因素,建立拖拉機牽引驅動模型,提出四輪驅動拖拉機田間牽引性能預測模型與求解算法,開展田間試驗,以期為農業動力裝備的牽引性能提升提供理論指導。
1 拖拉機牽引性能預測模型
拖拉機牽引驅動模型提出了預測田間性能的理論方法,對前后輪胎、前后軸、軸間、整機分別建模,包含土壤-輪胎模型、輪胎載荷模型、軸的驅動和載荷模型、前后軸間交互模型、整機驅動平衡方程和整機效率模型一系列數學模型。土壤-輪胎模型從單個輪胎的驅動特性入手,分別分析前后輪胎的附著性能。輪胎載荷模型考慮作業過程中的載荷轉移導致前后輪垂直載荷的動態變化,從而引起的前后輪胎附著性能的改變。前后軸間交互模型考慮軸間剛性連接的四輪驅動拖拉機前后軸運動不協調因素,得到避免功率循環的最小牽引力。對整機在前進方向、俯仰方向2個自由度建模,不考慮同一軸上左右輪胎的附著和載荷差異,將前后軸的驅動模型合并得到整機驅動平衡方程。通過引入滑轉效率、滾動效率及牽引效率模型,對四輪驅動拖拉機整機效率模型進行理論推導。
拖拉機牽引驅動模型包含超越方程組,求解算法是一個迭代過程,系統求解可得到整機牽引性能的重要評價指標為最大牽引力、滑轉效率、行走效率等,以及前后輪胎滑轉率、前后橋軸荷、前后橋驅動力的動態變化。
1.1 土壤-輪胎驅動模型
采用基于土壤圓錐指數的地面力學方法建立土壤-輪胎驅動模型[18-23]。模型中使用土壤圓錐指數,由圓錐貫入儀的圓錐體探針以穩定的速度插入土壤所需的每單位基底面積的力,用于表征土壤壓縮強度和抗剪強度的綜合特性[24]。在拖拉機一般耕作深度內,軟土或砂土圓錐指數通常為0~700 kPa,中等耕作土壤或壤土圓錐指數通常為850~1 200 kPa,堅實土壤或粘土圓錐指數在1 750 kPa以上[21]。在此基礎上引入輪胎指數,表示農用輪胎在兼具粘性與摩擦性質的土壤中的性能[19-20],其計算式為
(1)
式中Cn——輪胎指數
CI——土壤圓錐指數,kPa
b——輪胎斷面寬度,mm
d——輪胎直徑,mm
Fz——輪胎法向載荷,kN
考慮牽引過程中輪胎與土壤接觸時的徑向形變比和高寬比因素,引入輪胎機動指數Bn,表征在單個輪胎的牽引性能,隨著Bn增加,輪胎的牽引性能得到改善,用于修正輪胎指數,計算式為[21-22]
(2)
式中dΔ——輪胎徑向形變量,mm
h——輪胎斷面高度,mm
引入輪胎驅動力利用系數,定義為輪胎驅動力與法向載荷之比,是輪胎機動指數與滑轉率的函數,用來表征輪胎與土壤接觸面受到剪切應力-位移關系。計算式為
(3)
式中GTR——輪胎驅動力利用系數
GT——輪胎驅動力,kN
σ——輪胎滑轉率
定義滾動阻力系數為輪胎滾動阻力與法向載荷之比,是輪胎機動指數與滑轉率的函數,用來表征輪胎對土壤施加的法向載荷引起下陷而產生的行駛阻力。計算式為
(4)
式中MRR——輪胎滾動阻力系數
MR——輪胎滾動阻力,kN
定義輪胎牽引力利用系數為輪胎能夠產生的牽引力與法向載荷之比,由式(3)、(4)可得
NTR=GTR-MRR=
0.88(1-e-0.08Bn)(1-e-7σ)+0.03-
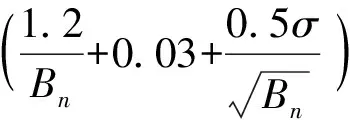
(5)
式中NTR——輪胎牽引力利用系數
由式(5)可知,土壤-輪胎互作過程中的牽引力利用系數可由土壤圓錐指數、輪胎斷面寬度與高度、徑向形變量、輪胎直徑等特征參數組成的函數表達,該模型可以有效表征輪胎載荷、土壤、輪胎等因素對拖拉機牽引性能的影響機理。
1.2 輪胎載荷模型
輪胎載荷模型是描述機組外載的作用下,前后輪胎的垂直載荷動態變化的方程組。圖1為拖拉機牽引受力分析情況。由圖1可知,在標準牽引試驗工況下,拖拉機質心位置與牽引力作用線均在整機縱向對稱平面內。

圖1 拖拉機牽引受力情況
從受力分析可知,四輪驅動拖拉機前后輪胎的滾動阻力矩為
Mf1=Fz1MRR1r1
(6)
Mf2=Fz2MRR2r2
(7)
式中Mf1——四輪驅動拖拉機前輪滾動阻力矩,N·m
Mf2——四輪驅動拖拉機后輪滾動阻力矩,N·m
Fz1——前輪地面法向反作用力,kN
Fz2——后輪地面法向反作用力,kN
r1——四輪驅動拖拉機前輪半徑,mm
r2——四輪驅動拖拉機后輪半徑,mm
引入土壤-輪胎驅動模型表征前后輪土壤、輪胎特性,可得包含輪胎機動指數的前、后輪地面法向反力計算式為
(8)
(9)
式中W——拖拉機實際重力,kN
L——拖拉機軸距,mm
Xcg——質心到后軸軸心的縱向距離,mm
hT——牽引點高度,mm
Ft——拖拉機整機牽引力,kN
1.3 拖拉機牽引驅動模型
拖拉機牽引驅動模型是計算滑轉效率和預測牽引性能的核心模型,是在輪胎驅動模型和載荷模型的基礎上,引入雙驅動橋的載荷分配、驅動特性以及整機驅動力平衡、運動不協調等拖拉機整機因素特征建立,具體為:
根據式(3)建立前、后輪胎驅動力利用系數計算式為

0.88(1-e-0.08Bni)(1-e-7σi)+0.03
(10)
式中i為1代表前輪,為2代表后輪。
根據式(4)建立前、后輪胎滾動阻力利用系數計算式為
(11)
根據式(10)、(11)建立前、后輪胎牽引力利用系數計算式為
NTRi=GTRi-MRRi=NTRi(Fzi,Cni,Bni,σi)=

(12)
設定拖拉機質心位置坐標與牽引力延伸線處于垂直于地面的同一平面內,則同驅動橋兩側的驅動輪載荷相等,由式(8)、(9)可得到前后橋軸荷計算式為
(13)
式中W1——拖拉機前驅動橋軸荷,kN
W2——拖拉機后驅動橋軸荷,kN
導出前后橋驅動力計算式為
(14)
式中Fq1——拖拉機前驅動橋驅動力,kN
Fq2——拖拉機后驅動橋驅動力,kN
拖拉機驅動力平衡方程為
Fq=Ft+FRR
(15)

(16)
(17)
(18)
式中Fq——四輪驅動拖拉機總驅動力,kN
FRR——拖拉機整機滾動阻力,kN
四輪驅動拖拉機牽引作業時,前后橋間的傳動系為剛性閉鎖式聯接,實際速度相等;由于前后驅動輪對土壤的壓實作用存在時序,且軸荷、輪胎規格不同,前后橋作業時的地面附著系數存在差異,因此需要針對四輪驅動拖拉機的前后橋分別設計不同的理論速度避免驅動輪出現嚴重滑轉現象,采用前后橋運動不協調系數表示前后驅動輪理論速度差異,計算式為
(19)
式中ε——前后橋運動不協調系數
VL1——前橋理論速度,km/h
VL2——后橋理論速度,km/h
拖拉機實際作業車速為
V=V1=V2
(20)
式中V——拖拉機實際作業速度,km/h
V1——前橋實際作業速度,km/h
V2——后橋實際作業速度,km/h
拖拉機理論作業車速為
(21)
式中VL——拖拉機理論作業速度,km/h
將式(21)代入式(20)可得
V=VL1(1-σ1)=VL2(1-σ2)
(22)
式中σ1——前輪滑轉率
σ2——后輪滑轉率
將式(19)代入式(22)推導出前后輪滑轉率與前后橋運動不協調系數的關系式為
σ1=σ2+ε(1-σ2)
(23)
四輪驅動拖拉機滑轉效率是整機驅動實際輸出功率與理論驅動功率之比,考慮前后橋運動不協調性后,整機理論驅動功率為前后橋總驅動功率,導出滑轉效率計算式為
(24)
式中ησ——四輪驅動拖拉機滑轉效率
將式(21)代入式(24)可得
(25)
由式(25)可知,滑轉效率可由前后橋驅動力分配及前后輪滑轉率的函數表征。結合式(3)、(5),可揭示四輪驅動拖拉機滑轉率同時受輪胎、土壤、拖拉機前后橋運動不協調的影響機理。
由式(15)、(18)可導出四輪驅動拖拉機滾動效率模型為
(26)
式中ηf——四輪驅動拖拉機滾動效率
由式(25)、(26)可導出四輪驅動拖拉機牽引效率預測模型為
ηT=ηDηc=ησηfηc=

(27)
式中ηT——四輪驅動拖拉機牽引效率
ηD——四輪驅動拖拉機行走效率
ηc——拖拉機傳動效率
將單個輪胎模型、驅動軸及軸間運動模型及整機模型組成四輪驅動拖拉機牽引驅動模型路線圖如圖2所示,該模型可有效表征四輪驅動拖拉機牽引效率受輪胎規格、土壤特性、整機前后橋運動不協調特性、傳動系統綜合影響的機理。

圖2 四輪驅動拖拉機牽引驅動模型建立技術路線圖
2 求解算法
由于模型內部和各模型間存在迭代的特性:整機牽引力的發揮是所有單個驅動輪能夠發揮的牽引力之和,單個輪胎的牽引特性是其法向載荷的函數,而單個輪胎上的法向反作用力取決于整機牽引力和前后驅動輪滾動阻力系數。模型無法自上而下或一次性計算求解,求解過程需要建立雙維度迭代算法。
求解算法及流程見圖3。內層將后輪滑轉率進行迭代,由前后橋運動不協調系數方程式(23)解出前輪滑轉率,由土壤-輪胎驅動特性式(10)~(12)分別解出前后輪胎的驅動力系數GTR、滾動阻力系數MRR及牽引利用系數NTR。由前后橋驅動力計算式(14)得到前后驅動橋驅動力。由拖拉機驅動力平衡方程(16)~(18)得到整機滾動阻力、牽引力、驅動力。外層將后輪法向載荷Fz2進行迭代,初始條件等于靜態載荷,按照5 N的步長更新,終止條件為后驅動橋軸荷W2達到為80%的整機重量。模型最終可求解出所有掛鉤牽引力范圍內的前后滑轉率、前后驅動力和滾動阻力,即可根據式(25)~(27)計算整機行走效率。

圖3 拖拉機牽引性能仿真流程圖
3 實例分析
以東方紅某165 kW拖拉機為實例,整機參數如表1所示,在土壤圓錐指數為1 725 kPa的農用土壤環境下,通過在Matlab環境中按照圖2中的模型建立路線圖分別建立土壤-輪胎模型、驅動軸及軸間運動模型、整機模型并按照圖3中的流程建立求解算法,建立數學模型開展仿真分析。

表1 實例分析整機參數
圖4為土壤-輪胎驅動特性情況。其中圖4a為前后輪驅動利用系數與牽引力的關系,由圖4a可知,牽引力范圍內,前輪的驅動利用系數始終高于后輪;當牽引力達到特征值時,GTR1=0.71,GTR2=0.68;主要原因是前橋的靜態軸荷小于后橋,前驅動輪的法向載荷較小,隨著牽引力逐漸增大,質心位置后移,前橋減重,后橋增重,前輪驅動力利用系數的變化率小于后輪。

圖4 土壤-輪胎驅動特性
圖4b為前后輪胎滑轉率情況。由圖可知,當Ft<2.7 kN時,σ1>0,σ2<0,VL1>V>VL2;由于前后橋運動不協調,整機前驅動輪理論速度較高,驅動力較大,滑轉較高;在整機的推進作用下,后驅動輪理論速度小于整機推進速度,同時出現滾動與滑移,對整機起到了制動作用。產生這種情況的原因是當牽引載荷較低時,由于前后橋運動不協調性導致前、后理論速差較大,四輪驅動拖拉機出現了明顯的功率循環。當Ft=2.7 kN時,σ1>0,σ2=0,VL1>V=VL2,此時后驅動輪呈純滾動狀態。當Ft>2.7 kN時,σ1>σ2>0,VL1>VL2>V,前后驅動輪都出現了滑轉的情況,功率循環消除,前后輪胎均發揮驅動作用;此時由于運動不協調系數導致前驅動輪理論速度較高,滑轉率較大。
圖4c為前后輪滾動阻力系數與牽引力的關系。由圖4c可知,滾動阻力系數隨掛鉤牽引力而增大。當牽引力達到容許特征值之前,輪胎的滾阻系數的增加較小,MRR1=0.049~0.055,后輪滾阻系數MRR2=0.045~0.062。當牽引力超過容許特征值后,由式(4)可知,前后輪滑轉率快速增大,引起了滾動阻力系數的快速增加。當牽引力增大到80 kN左右,輪胎滾動阻力系數快速增大,導致整機滾動阻力的快速增大,引起牽引力下降,得出該型號四輪驅動拖拉機在土壤圓錐指數為1 725 kPa的農用土壤環境下的最大牽引力為80 kN。
圖5為前后橋載荷與驅動特性。圖5a為前后橋軸荷與牽引力的關系,由圖5a可知,由于軸荷轉移情況與牽引力大小呈線性關系,W1隨Ft的增大而減小,W2隨Ft的增大而增大。當Ft達到容許特征值時,W1=31.4 kN,占整機重力的32%,前橋軸荷減重達到24.4%。圖5b為前后橋驅動力與牽引力的關系,由圖5b可知,當Ft≤16.4 kN時,Fq1≥Fq2,前橋分配的驅動力較大;當Ft>16.4 kN時,Fq1 圖5 前后橋載荷和驅動特性 圖6為四輪驅動拖拉機牽引性能計算結果。由圖6可知,整機在容許滑轉率點A時的牽引力為62.8 kN,行走效率為0.731,滾動阻力系數達到0.06;在行走效率最高點B處牽引力為36 kN,行走效率為0.802,滑轉率為0.081,滾動阻力系數為0.052。根據國家拖拉機質量檢驗檢測中心出具的該型號拖拉機標準跑道環境的牽引性能試驗報告,整機達到容許滑轉率時的行走效率為0.86,最高行走效率可達0.93,對照分析結果可知,實際農用土壤條件對四輪驅動拖拉機牽引性能的影響較大,降幅為10%~15%。此外圖中,當ησ=0.8時,即滑轉率達到特征滑轉率0.2時,四輪驅動拖拉機Ft達到容許特征值62.8 kN。對照圖4b可以看出,此時,σ1=0.211,超過容許滑轉率;σ2=0.195,低于容許滑轉率,說明建立的滑轉效率模型體現出了四輪驅動拖拉機前后橋運動不協調性與前后輪胎-土壤附著性能差異,有效性較好。 圖6 牽引性能計算結果 開展實機田間牽引負荷測試,驗證提出的牽引性能預測方法的有效性。試驗總體參照GB/T 3871.9—2006《農業拖拉機試驗規程 第9部分 牽引功率試驗》開展,被試對象為實例分析對象拖拉機,輪胎胎壓、整機參數如表1所示。試驗地點為洛陽拖拉機研究所有限公司孟津崔溝田間全地型試驗場,測試環境為玉米茬地,測試土壤圓錐指數為650 kPa左右。被測變量為牽引力、不同牽引力下的前后輪胎滑轉率、輪胎滾動阻力。試驗采用TY160型負荷車、PCM-6851型車輛綜合性能測試儀、OMRON E6B2-CWZ3E型轉數傳感器和BLR-1M10T型拉壓力傳感器。 圖7為田間試驗原理及主要試驗設備情況。試驗過程中,負荷車加載最大功率為175 kW,最大加載力為120 kN,負載牽引力從0 kN開始,以1 kN為步長線性增加,至驅動輪全滑轉后終止增大;測試作業距離取40 m;測試速度為3.5 km/h。被測變量的測試方法為: 圖7 試驗原理及主要試驗設備 牽引力:被試拖拉機與負荷車之間通過拉壓力傳感器和鋼索連接,由安裝在拖拉機牽引掛鉤處的拉壓力傳感器測量負荷車施加的牽引力。 輪胎滑轉率:滑轉率無法直接測量,采用同一距離法測量拖拉機在負荷車施加的不同牽引負載下作業相同距離驅動輪轉過的圈數,前后驅動輪轉動的圈數由安裝在拖拉機驅動輪上的霍爾傳感器測量,根據驅動輪圈數計算輪胎滑轉率為 (28) 式中σ′i——輪胎滑轉率測量值 NAi——無牽引負載狀態下輪胎轉過的圈數 NBi——逐漸增加牽引負載后輪胎轉過的圈數 輪胎滾動阻力:測試滾動阻力時,被試拖拉機發動機熄火、掛空擋,使傳動系主離合器完全分離后,由負荷車反向拖動被試拖拉機,由拉壓力傳感器測量得出滾動阻力。 通過河南科技大學設計的車輛綜合性能測試儀對單一采樣步長內的拉力、輪胎轉動圈數等信號進行整合處理,得出測試過程中的牽引力、輪胎滑轉率、輪胎滾動阻力;上傳至上位機端。 依照與試驗相同的拖拉機整機參數及土壤環境,在Matlab環境中建立該實例拖拉機的田間牽引性能預測模型,得到仿真結果。選擇相關研究[15]中使用的拖拉機牽引性能模型作為對照組,并建立對照組模型,開展對比分析。將仿真、試驗數據與相關研究中的對照組結果進行對照,結果如圖8所示。 圖8 滑轉率、滾動阻力試驗值和仿真值對比 圖8a為滑轉率對照結果,對比在該點處的仿真值、試驗值及對照組的值,如表2所示。采用提出的四輪驅動拖拉機田間牽引性能預測分析結果中,整機全滑轉時的最大牽引力仿真值為64.8 kN,特征滑轉率對應的牽引力仿真值為51.2 kN;最大牽引力試驗值為63.9 kN,特征滑轉率對應的牽引力試驗值為49.9 kN;仿真值在最大牽引力與特征滑轉率對應的牽引力上的誤差分別為1.41%與1.74%。對照組中,最大牽引力仿真值為38.1 kN,特征滑轉率對應的牽引力為26.5 kN,在最大牽引力與特征滑轉率對應牽引力上的誤差分別為40.37%與46.89%。提出的四輪驅動拖拉機田間牽引性能預測模型對滑轉率、滑轉效率等指標的仿真精度較好。 表2 仿真值、對照組與試驗值特征指標對比 圖8b為滾動阻力指標對照結果。由圖8b及表2 可知,提出的四輪驅動拖拉機田間牽引性能預測分析結果中,未施加負載牽引力時的滾動阻力仿真值為7.78 kN,最大牽引力仿真值為64.8 kN,當牽引力超過64.8 kN后,滾動阻力持續增大,降低牽引力輸出能力;未施加負載牽引力時的滾動阻力試驗值為7.83 kN,誤差為0.64%;對照組中,滾動阻力仿真值始終保持為6.97 kN,未施加牽引力處的誤差為10.9%,誤差較大。此外,由滾動阻力測試方法可知,試驗過程中僅能通過負荷車反向拖動的情況測試出未施加牽引力狀態下整機的滾動阻力,當施加牽引力后,拉壓力傳感器僅能測出施加在拖拉機牽引掛鉤上的牽引力,因此難以有效測出加載狀態下拖拉機滾動阻力的具體變化情況;但是,從滑轉率測試結果中對照仿真值與試驗值的最大牽引力指標對比情況可以看出誤差較小,可以證明滾動阻力仿真的效果較好。 由圖8可知,仿真值總體上可以較為準確地體現出牽引性能核心指標牽引力、滑轉率、滾動阻力的變化趨勢,采用均方根誤差(Root-mean-square error,RMSE)評價模型的有效精度。計算可得,提出的四輪驅動拖拉機田間牽引性能預測分析仿真值滑轉率均方根誤差為0.023 7,滾動阻力均方根誤差為0.23 kN; 對照組滑轉率均方根誤差為0.219,滾動阻力均方根誤差為1.66 kN。因此,提出的四輪驅動拖拉機田間牽引性能預測分析方法總體與實測值的偏差較小,模型的準確度較高。 (1)通過建立土壤-輪胎驅動模型、輪胎載荷模型與拖拉機牽引驅動模型,導出了包含輪胎規格、土壤特性、整機前后橋運動不協調特性、傳動效率的四輪驅動拖拉機牽引效率預測模型,揭示了影響機理。 (2)提出了基于雙維度迭代的牽引性能預測算法,制定了求解流程,有效解決了模型多變量、非線性導致的求解難題;開展了實例分析,預測了四輪驅動拖拉機在農用土壤條件下的牽引力、滑轉率、滾動阻力、牽引效率等牽引性能指標。 (3)設計了田間牽引試驗方案,選擇現有預測模型作為對照組,開展了試驗,結果表明:農用土壤條件下,對照實測值,提出的牽引性能預測方法中滑轉率均方根誤差為0.023 7,滾動阻力均方根誤差為0.23 kN,總體偏差較小,較對照組精度提升較大,驗證了提出的四輪驅動拖拉機田間牽引性能模型及預測方法的有效性。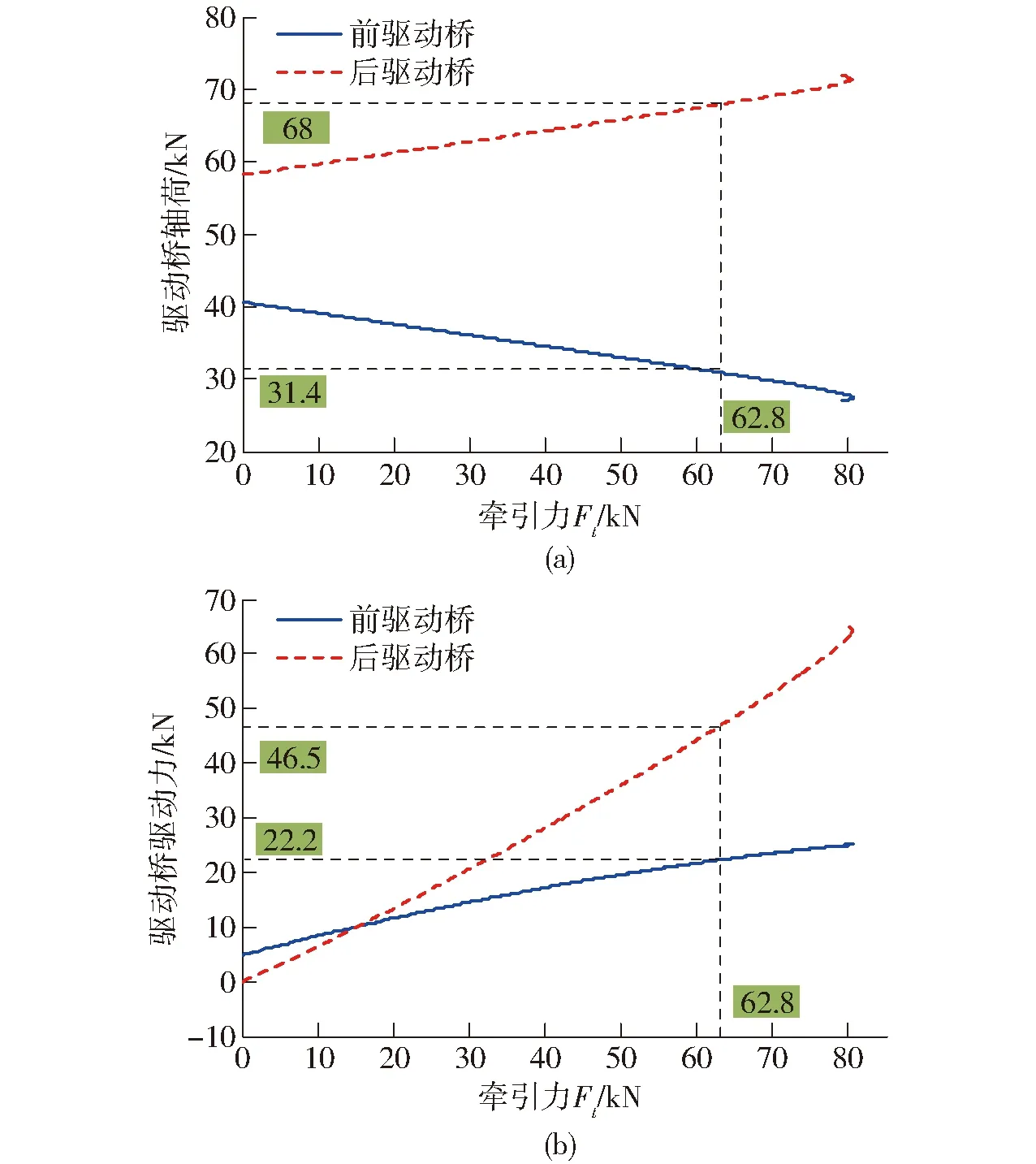

4 試驗驗證



5 結論

