流速對系泊球形潛體動力特性及尾渦結構的影響研究*

蔣濟同, 劉瑞慶, 周獻祥

(1. 中國海洋大學工程學院, 山東 青島 266100; 2. 軍事科學院國防工程研究院, 北京 100036)

隨著油氣資源消耗的日益增加,海洋資源的開發和利用受到越來越多國家的重視,大力發展海洋油氣對于中國社會發展的需要和經濟結構的調整都具有重要意義,而深海資源的開發離不開各類具備操縱性能的水下作業設備的支持[1]。

懸置海洋中部構筑物使用系泊纜固定在特定水深,不具備自主航行能力。可以為水下潛器提供燃料以提高水下作業設備的持久性,同時可以搭載傳感器對海洋環境進行長期的監測,以及為深海活動提供設備上的支持,為人類進一步對深遠海環境的勘察和油氣等資源的開發和利用提供有力的支持。韋起賢[2]使用雙向流固耦合的方法,對不同形狀的潛體進行了動力響應分析并做了形狀的優選。牛云龍[3]研究了影響潛體安全性和實用性的因素,并通過AQWA軟件對三索三點和單索單點進行比較,分析不同的系泊方式對構筑物運動響應的影響。曠俊[4]使用AQWA軟件對單索單點系泊球型構筑物進行了動力響應研究。由于勢流是無旋性速度場,因此,基于勢流理論的AQWA軟件在計算繞流體在水流中的動力響應問題時忽略了多種因素的耦合影響,無法捕捉潛體運動時流場的變化和潛體的運動特性。

本文采用較為直觀的在實驗水池中進行模型試驗的方法,以及目前發展比較成熟的計算流體力學的方法來研究球形潛體在不同流速下的運動響應問題。首先根據實驗室條件設計了針對球形潛體模型的水動力試驗,試驗模型為3D打印的直徑為0.2 m的球形潛體,系泊纜選用細軟的高強度魚線,魚線質量與尺寸遠小于球形潛體尺寸,所以在使用數值實驗方法研究球形潛體的運動特性時不考慮系泊纜的影響。數值計算使用ANSYS軟件的雙向流固耦合模塊,為了更廣泛地研究流速對球形潛體運動特性的影響,在實驗室0.3和0.5 m/s工況的基礎上,數值實驗增加了0.1、0.2和0.4 m/s三個工況。

1 三維繞流數值模擬

1.1 SST k-ω 湍流模型方程

CFD常用的湍流計算模型包括LES、k-ε、k-ω等。目前被廣泛使用的大渦模擬法(LES)精度較高,是計算繞流模型比較理想的計算模型,然而存在計算效率低的問題。在近壁面問題的處理上,相對于k-ε模型采用壁面函數SSTk-ω模型在近壁面處采用k-ω,對邊界層網格進行直接求解;主流區則采用k-ε,近壁面處理較好,能準確預測升力與阻力。所以在綜合考慮計算效率和計算精度這兩個因素后,本研究選擇SSTk-ω湍流計算模型進行后續的計算。Menter[5]在標準k-ω模型中加入交叉擴散項,并在湍流黏度定義中考慮了湍流剪切應力的傳遞,得到了 SSTk-ω模型:

(1)

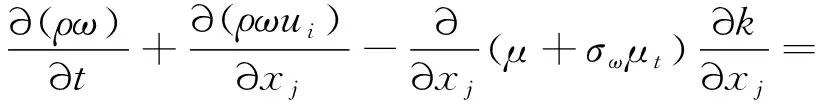
(2)

式中:Gk為湍動能生成項;Gω為比耗散率生成項;Yω和Yk分別為ω和k的耗散項;μ為來流動力黏性系數;Dω為交叉擴散項;ρ為來流密度[6]。

1.2 參數設置

圖1 流體域

1.3 糙率設置

水動力試驗方案中使用的模型根據糙率相似準則設計模型尺寸,數模糙率設置參考有機玻璃的糙率范圍。購買一個糙率為0.008 5的標準有機玻璃材質模型,對試驗模型進行砂紙打磨,使其糙率更加接近有機玻璃的糙率,比較兩種不同材料的模型在水流作用下的運動響應和受力情況[4]。由圖2(a)和(b)可知兩種材料的球形潛體順流向(x軸方向)和逆流向位移的誤差均在10%以內,說明試驗模型的糙率和有機玻璃模型的糙率是接近的。將試驗模型的糙率認定為0.008 5,數值模型的糙率相應的設置為0.008 5。

((a)不同材料的球形潛體順流向運動響應對比;(b)不同材料的球形潛體橫流向運動響應對比。(a) Comparison of downstream motion responses of spherical submersibles made of different materials; (b) Comparison of cross flow motion responses of spherical submerged bodies made of different materials.)

1.4 重疊網格

本文研究的球形潛體運動問題包含了潛體的大幅度擺動和轉動,之前的做法是使用傳統動網格的方法計算,但是傳統動網格在使用過程中需要頻繁地使用平順、鋪層和網格重新生成這些操作,這些復雜操作在繞流固體位移過程中不僅要花費更多時間,而且容易產生計算不收斂問題[7],重疊網格方法的使用很大程度上解決了網格運動可能產生的這些問題,而且可以選擇精度相對更高的六面體網格代替四面體網格,通過結構化網格劃分來提高網格質量,進而提高計算精度,使繞流固體運動的計算更加高效和精確。Steger等[8]最早提出重疊網格,其方法是將網格分成貼體網格和背景網格兩部分,兩套網格重疊,且網格不用共點或共面。重疊網格的背景網格和貼體網格示例如圖3(a)所示。

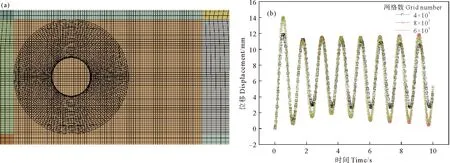
((a)重疊網格剖面;(b)不同網格數運動響應結果對比。 (a) Overlapping grid sections; (b) Comparison of motion response results with different grid numbers.)

為進一步減小網格對計算結果的影響并減輕計算負擔,這里選用3套網格數量(432 325、632 253和833 625個六面體單元網格)進行結果對比。從圖3(b)可知,40萬個網格的計算結果與60萬個網格的計算結果相差6%,而60萬網格的計算結果同80萬個網格的計算結果相差小于1%,說明60萬個網格已經趨于收斂,因此下文的數值實驗計算均使用60萬個網格。

2 結果分析

2.1 順流向與橫流向運動響應幅值及均方根對比

本文用0.3和0.5 m/s兩個試驗工況的結果校正數值實驗模型,并用校正后的計算模型對流速為0.1、0.2和0.4 m/s的工況進行計算。經計算,模型穩定后的試驗結果和數值實驗結果中順流向平均位移分別為6.39和6.31 mm,兩者平均位移吻合較好。由于雙向流固耦合計算量較大,本文在模型試驗與數值實驗的潛體模型運動穩定后,各取20 s結果做比對,圖4分別給出了工況為0.3和0.5 m/s時兩者在順流向及橫流向上的運動響應。

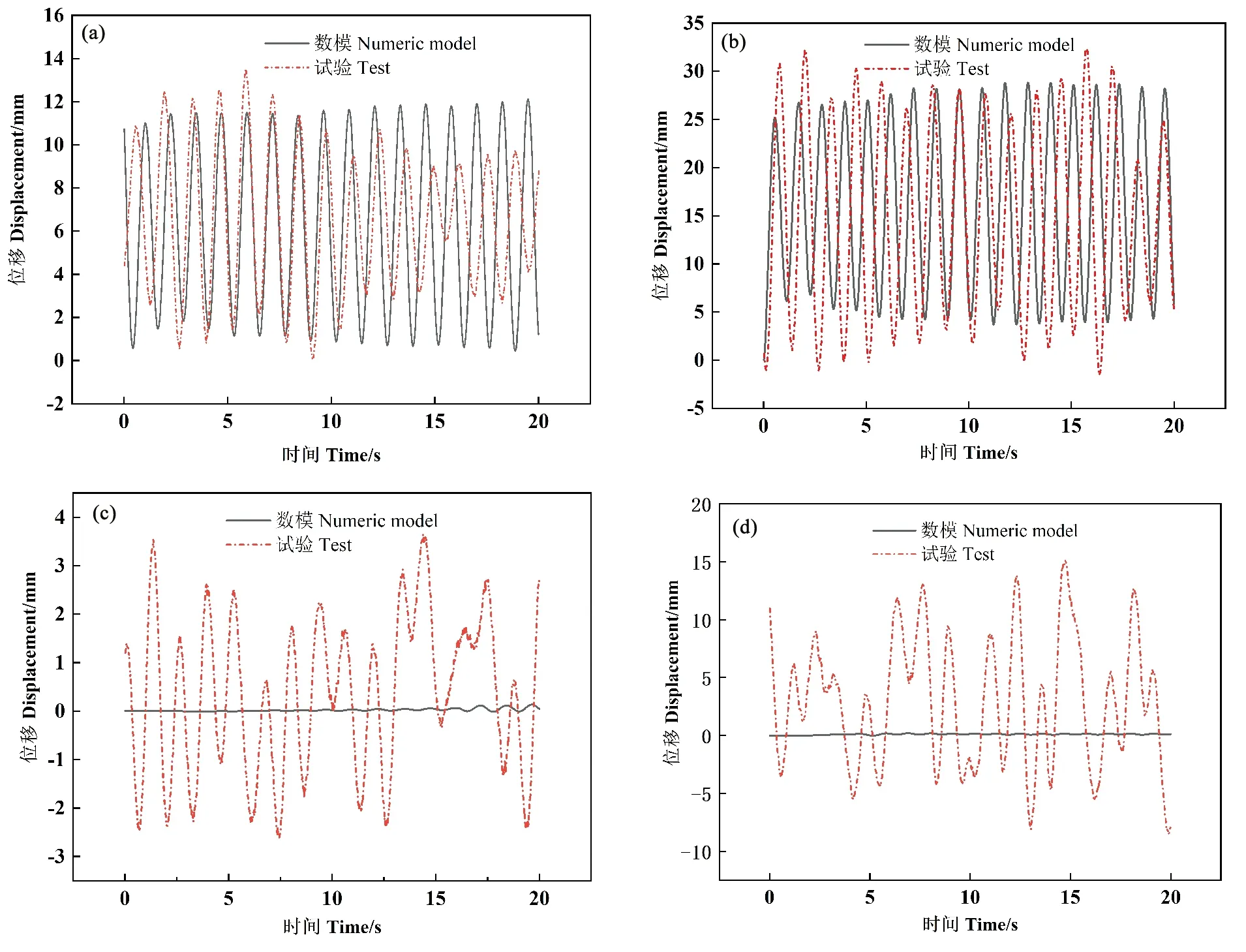
((a) 0.3 m/s順流向運動響應對比; (b) 0.5 m/s順流向運動響應對比; (c) 0.3 m/s橫流向運動響應對比; (d) 0.5 m/s橫流向運動響應對比。 (a) 0.3 m/s downstream motion response comparison; (b) 0.5 m/s downstream motion response comparison; (c) 0.3 m/s cross flow motion response comparison; (d) 0.5 m/s cross flow motion response comparison.)

圖4(a)為潛體模型在順流向上流速為0.3 m/s時數值實驗結果和試驗結果的比對,兩者變化趨勢保持一致,平均值相同,數值實驗結果的運動幅值相對于試驗結果要更加穩定,這是因為基于RANS方程的SSTk-ω湍流模型將非定常流轉化為定常流問題,只能計算平均流動,不能計算流體的所有細節。圖4(b)是順流向上流速為0.5 m/s時數值實驗結果和試驗結果的對比,兩者平均值大致相同,運動幅值也基本吻合。

圖4(c)和圖4(d)分別為模型在流速為0.3和0.5 m/s時橫流向數值實驗結果和試驗結果的比對,2個流速下數值模擬的運動幅值均遠小于試驗結果。考慮到試驗模型內部貼附的配重塊不能均勻分布在球身上,這使得模型存在重心偏移,即圓球的重心和球心不重合,并且手工打磨拋光的球形潛體模型的外形、糙率和標準的數值模型存在一定誤差。猜測是圓球重心偏移、幾何中心偏移以及糙率的誤差均影響了模型試驗中潛體的橫向位移,同時流速從0.3 m/s增大到0.5 m/s,又放大了這個偏差。針對這個猜測,建立了一個幾何中心和重心偏移12%的模型,在流速為0.5 m/s工況下重新計算發現,橫流向出現了小幅度位移,證實了圓球重心和幾何中心的偏移會影響潛體的橫向位移,但尚無法準確量化試驗所用模型的重心和幾何中心的偏移程度,以及糙率誤差的大小,模擬無重心和幾何中心的偏移潛體是研究潛體運動響應的一個階段性工作,下一步工作將研究數值模型的重心和幾何中心的偏移計算,并在之后的模型試驗設計中要著重考慮試驗模型制作的重心和幾何中心的偏移問題。

為了更直觀地對比數值實驗與試驗兩者的運動幅值結果,將5個工況的計算結果一并進行均方根處理并分析。圖5(a)為順流向運動無量綱均方根幅值,數值實驗順流向的結果與試驗結果走勢相同,隨著流速的增大總體呈增大趨勢,并且隨著流速的增大無量綱均方根幅值的增幅變大。其中:在流速為0.3 m/s工況下數值模擬結果為0.19,略大于實驗結果的0.17;在流速為0.5 m/s工況下數值實驗結果為0.42,小于實驗結果的0.51。圖5(b)橫流向無量綱均方根幅值,數值實驗結果靠近0附近,試驗結果分別為0.08和0.27,均大于0,這是因為在前期制作試驗模型過程中,給模型加的配重塊不能均勻分布在球身,導致模型在橫流向上的運動偏向一側。

((a)順流向運動幅值無量綱均方根;(b) 橫流向運動幅值無量綱均方根。(a)Dimensionless root mean square of down stream motion amplitude; (b) Cross flow motion amplitude dimensionless root mean square.)

2.2 圓周壓力系數

圖6給出了在Z=0高度處截取壓力系數沿圓周的分布特性。圖中θ為XY平面方位角,球體的前駐點為0°,順時針方向為正方向,后駐點為180°。由于模型沿著順流向的中心線是對稱的,所以各工況的壓力分布也是沿著中心線對稱分布的。各工況的最高壓力出現在0°處,隨著角度的增加壓力急劇下降,在迎流面上形成正壓力梯度,使表面的邊界層加速流動,在70°～90°之間表面壓力達到最小,速度達到最大,稱為順壓區。經過這個區間后外部的勢流及邊界層開始減速加壓,在剪應力和逆向壓力梯度的雙重作用下邊界層流體動能減小,開始出現邊界層分離,稱為逆壓區。隨著流速的增加,表面分離點滯后,具體表現為當流速為0.1、0.2和0.3 m/s時壓力最小點均出現在78°的位置,當流速為0.4和0.5 m/s時壓力最小點均推后到85°處,分離點位置的變化影響著球形潛體的阻力,球形潛體的阻力主要包括摩擦阻力和壓差阻力,其中壓差阻力要比摩擦阻力大得多[9]。分離點位置越靠后,球形潛體的前后壓差就越小。根據圖6可知,隨著流速的增大,分離點呈后移趨勢,即前后壓差減小,更易克服逆壓梯度。

(黑色線代表0.1 m/s工況,橙色線代表0.2 m/s工況,藍色線代表0.3 m/s工況,綠色線代表0.4 m/s工況,紫色線代表0.5 m/s工況。The black line represents 0.1 m/s, the orange line represents 0.2 m/s, the blue line represents 0.3 m/s, the green line represents 0.4 m/s, and the purple line represents 0.5 m/s.)

2.3 St數

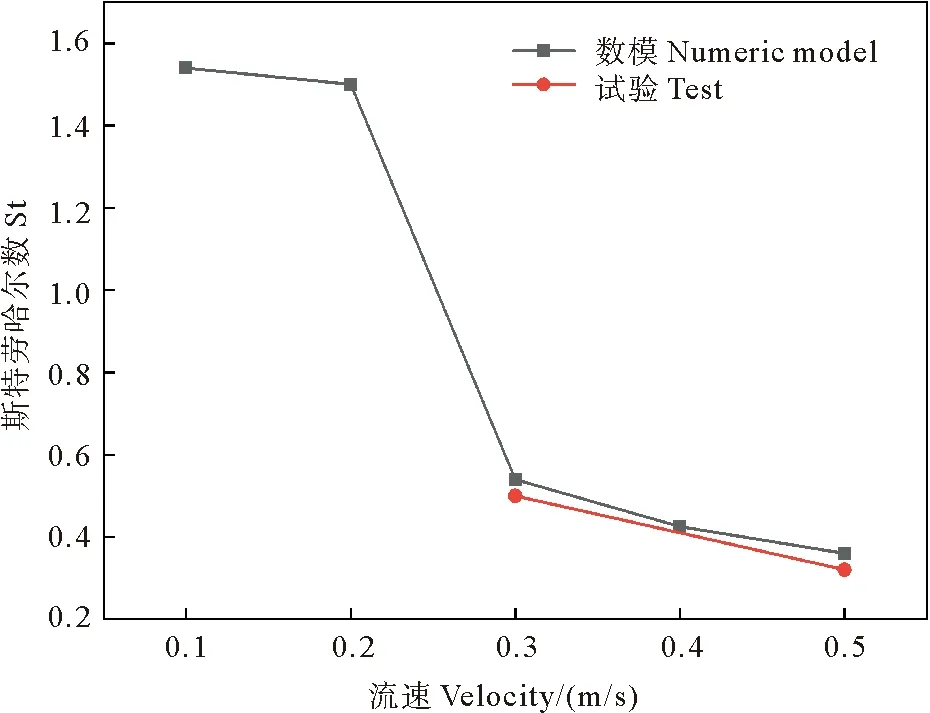
圖7 St數隨速度的變化

2.4 尾渦形態分析

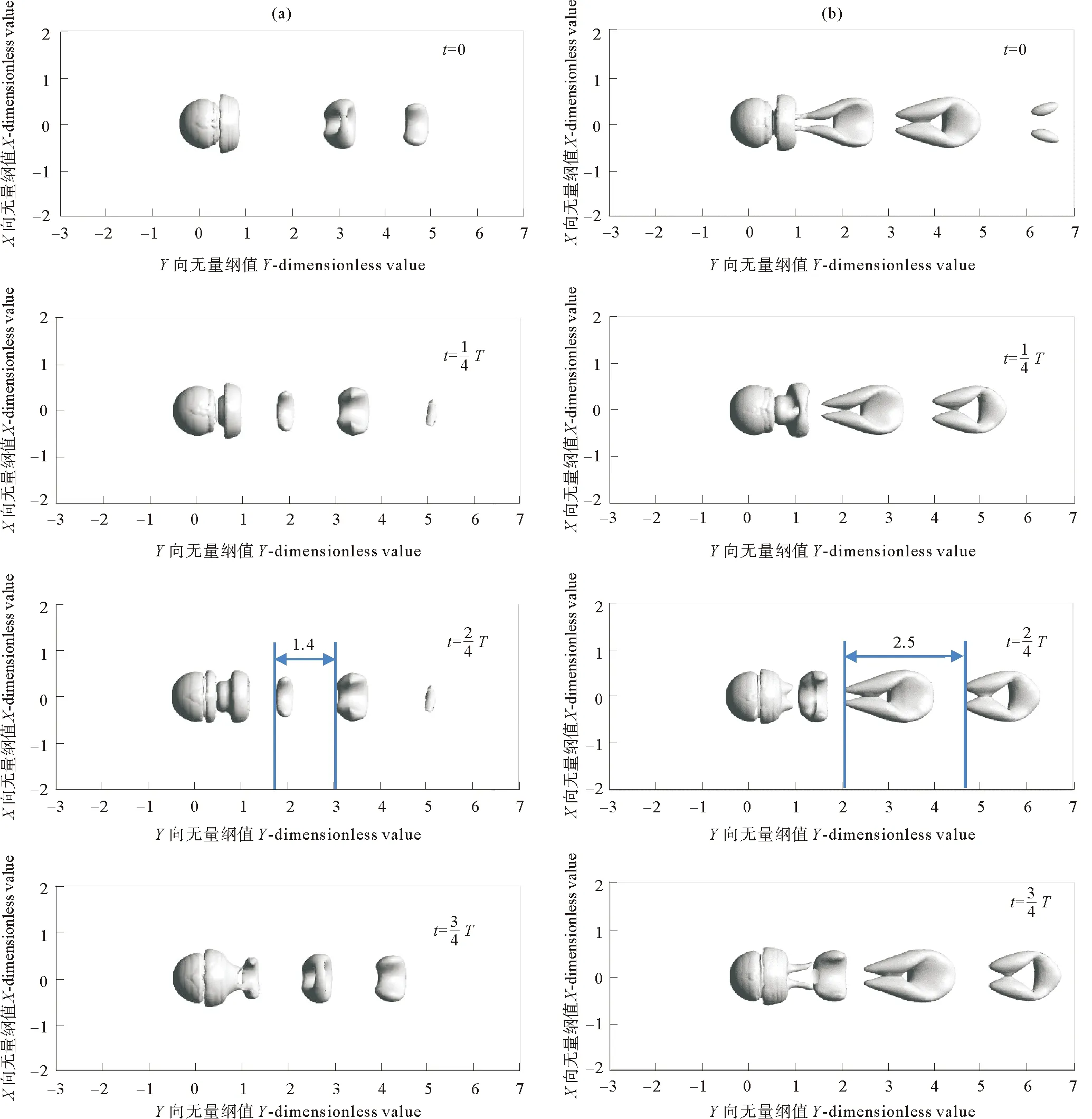
(橫坐標表示流場順流向尺寸Y與潛體直徑D的比值:Y/D;縱坐標表示流場橫流向尺寸X與潛體直徑D的比值:X/D。The horizontal axis represents the ratio of the downstream dimension Y of the flow field to the diameter D of the submerged body: Y/D; The vertical axis represents the ratio of the transverse dimension X of the flow field to the diameter D of the submerged body: X/D.)

(橫坐標表示流場順流向尺寸Y與潛體直徑D的比值:Y/D;縱坐標表示順流向流速Uy與入口初始流速U0的比值:Uy/U0。The horizontal axis represents the ratio of the downstream dimension Y of the flow field to the diameter D of the submerged body: Y/D; The vertical axis represents the ratio of the downstream flow velocity Uy to the initial inlet flow velocity U0: Uy/U0.)

3 結論

(1)順流向上模型的運動響應數值實驗結果同試驗結果吻合很好,模型的運動幅值無量綱均方根同數值模擬結果基本一致,兩者走勢相同,隨著流速的增大總體呈增大趨勢。

(2)隨著流速增大,模型的分離點呈后移趨勢,且在0.3和0.4 m/s流速下分離角驟增,分離點后移,即前后壓差減小,隨著流速的增加球形潛體更易克服逆壓梯度。

(3)隨著流速的增加St數呈下降趨勢,且在0.3和0.5 m/s工況處的數值模擬結果和試驗結果一致。由于雷諾數在103～104范圍內高頻率(渦脫落的頻率)的存在直到6×104[10],流速從0.2 m/s增大到0.3 m/s時,St數出現驟降。

(4)模型分離點隨著流速的增大而后退,即渦結構從圓球表面脫離的位置更加靠后,這使得渦結構的形狀發生變化,表現為0.5 m/s工況下渦結構的初始形態由開始的圓環狀被拖拽成水滴狀。脫落的渦結構之間的間隔隨著流速增大而變大,更大的流速產生更大的渦量,更大渦量的渦結構可以傳播到更遠的位置,其中,在順流向的中軸線上,每個渦結構的核心處也是流速的極大值。