基于卷積濾波的接觸式紗線張力測量方法

彭來湖, 劉建廷, 李 楊, 齊育寶, 李建強, 茅木泉

(1. 浙江理工大學 浙江省現代紡織裝備技術重點實驗室, 浙江 杭州 310018; 2. 浙江理工大學龍港研究院有限公司, 浙江 溫州 325802; 3. 杭州高騰機電科技有限公司, 浙江 杭州 310018)

隨著紡織設備的發展,對紗線張力的穩定性要求也越來越高[1]。紡織品生產過程中,紗線張力的大小對產品品質和生產效能有重要影響[2]：張力過大會出現斷紗、停機或者稀密緯的現象;張力過小時,織物會出現褶皺等現象;在紗線輸送過程中,紗線的張力在一定范圍內處于高頻振動狀態,給張力調節系統帶來了很大的影響,所以實時監控紗線張力的峰值,保持紗線張力穩定輸送對提高針織產品的質量非常重要[3-4]。

在紗線張力研究方面:孫帥等[5]測試了不同速度下紗線張力的波動變化,得出生產速度與紗線張力的波動規律;陳紅霞等[6]用標準差來評價張力整體的波動情況;章鈺娟等[7]提出了一種基于紅外光投影的光電感應檢測方法,可用來減少儀器對紗線輸送狀態的影響,以此來提高張力檢測的準確性;吳震宇等[8]建立了一種接觸式紗線張力傳感器的動態模型,利用測量模型計算出的誤差抑制算法有效地消除了振動產生的張力檢測誤差。國外有學者對經編紗線運動過程進行研究分析。Vítor Carvalho等[9]研究了一種用于測定紗線質量特性的自動系統,檢測直徑1 mm范圍內的紗線張力,由于采樣頻率過低無法應用于實際工作;Mikolajczyk 等[10]建立了送紗的數學模型認為,紗線與張力桿基本垂直時,經紗張力最大值相對較小;Jafaripanah等[11]提出了模擬技術濾波用于誤差信號的抑制。以上大多數研究是針對紗線振動特性、張力采集、濾波消除檢測誤差等方面,但在實際生產應用中,紗線張力的波動對紗線張力調節系統具有較大的影響,即波動會導致調節系統的張力反饋輸入信號有較大的偏差,導致輸出張力更加不穩定。因此在張力調控系統中不僅需要消除紗線張力誤差,還需要將獲取的處于波動狀態的紗線張力處理成穩定的張力輸出,供紗線張力調節系統使用。

本文提出了基于卷積濾波的紗線張力測試方法,通過懸臂梁結構設計出的張力傳感器,通過濾波和卷積算法處理采集到的電壓波動信號,濾除測量中的突變信號和高頻信號,然后進行平滑處理,實時獲取穩定的紗線張力值。

1 紗線張力特征分析

輸紗器與針筒以一定速比喂送紗線編織成圈時,受織針和輸紗器動態牽拉與輸送作用,紗線張力在保持相對恒定的同時,會出現高頻波動。對其進行分析可知:一方面紗線由織針進行牽拉編織,是一個間歇式變速拉扯紗線彎曲成圈過程,具有周期性運動特征;另一方面紗線本身具有一定彈性,拉伸狀態在周期性牽拉力作用下,紗線體內的應力波在傳遞過程中亦會出現散射、反射,其顯性表現為紗線張力高頻波動。

以高速無縫內衣機為例,針筒圓周布針 1 248枚,工作高轉速為125 r/min,則單根紗線牽拉成圈周期(T)為

(1)

成圈頻率(f)為

(2)

則紗線張力測量的最高頻率為2.6 kHz。張力傳感器應滿足這一最高頻率響應要求,同時,在保證紗線張力信號放大且不失真的前提下,應濾除高于此頻率的信號。

2 接觸式紗線張力測量方法

2.1 測量方案設計

紗線張力檢測主要目的是為紗線輸送提供恒張力閉環控制,根據紗線在喂送編織成圈過程中的張力特征及送紗張力控制要求,設計如圖 1所示的紗線測量和信號處理方案。首先張力信號通過懸臂梁結構從物理信號轉變成應變片的電信號,直接轉換的電信號非常微弱,無法直接進行采集,因此應將該信號經過閉環增益電路環節進行差分放大,接下來通過核心控制芯片進行數據采集,最后根據信號特征對信號進行限幅、低通、S-G卷積平滑處理,輸出穩定的紗線張力。

圖1 紗線測量和信號處理方案Fig. 1 Yarn measurement and signal processing scheme

2.2 傳感器結構設計

設計基于懸臂梁的紗線張力傳感器,紗線受力分析如圖2所示。其中:A為受力點;θ1,θ2為夾角,(°);f為合力,cN;fy為紗線張力,cN。圖內區域2和區域3是孔套,固定在基座;區域1是懸臂梁設計成Z型結構,一端固定在基座,另外一段倒成半圓柱,覆涂陶瓷,孔套亦用陶瓷材料燒結,以抵抗紗線磨損。A點、B點、C點,構成等腰三角形,紗線從B點進入,從C點出去,在A點緊壓陶瓷圓柱,將紗線張力傳遞給懸臂梁。三角形力傳遞結構一方面可減小紗線輸送過程中由于張力變化造成垂向抖動的干擾,使得測量更加準確;另外一方面也可通過調整頂角角度盡可能減小測量對紗線本體的磨損,以及對紗線輸送運動產生影響。

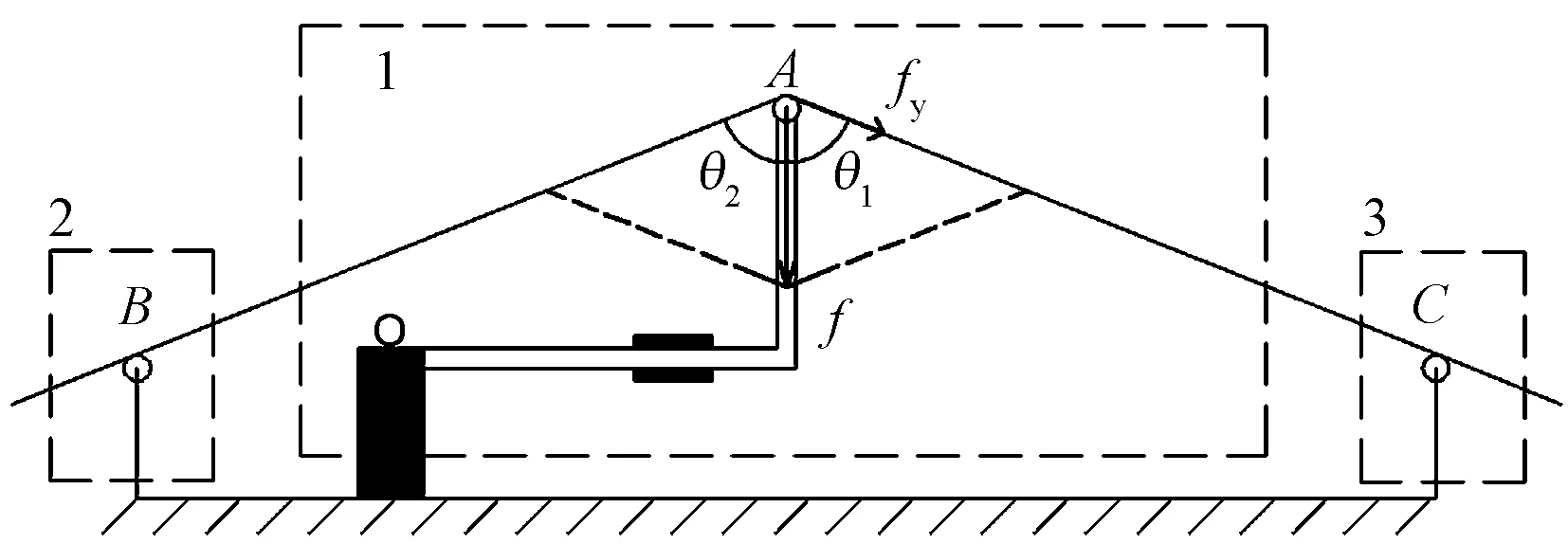
圖2 紗線受力分析圖Fig. 2 Stress analysis diagram of yarn

根據力的平行四邊形法則可知,垂直于懸臂梁自由端的合力f與紗線張力fy的關系為

f=fy(cosθ1+cosθ2)

(3)

2.3 懸臂梁模態分析

紗線張力傳感器結構中的懸臂梁在特定頻率作用力下會產生諧振響應,進而影響張力檢測,因此進行仿真分析校驗。懸臂梁結構如圖3所示。其中:a為寬度,mm;d為懸臂梁厚度,mm;l為長度,mm。

圖3 懸臂梁結構示意圖Fig. 3 Structural diagram of cantilever beam

懸臂梁彎曲振動控制方程為

(4)

式中:E為彈性模量,MPa;J為慣性矩,mm4;ρ為懸臂梁的密度,kg/m3。

紗線受本身張力波動、環境干擾的影響,傳感器信號具有較豐富頻譜特征;而且紗線張力峰值受機械故障影響,可能有較大數值。為防范懸臂梁出現共振、斷裂現象,設計如圖 4所示的懸臂梁結構:a= 10 mm,l=20 mm。d=2 mm,創建ANSYS模型針對懸臂梁結構進行應變、形變和模態分析。

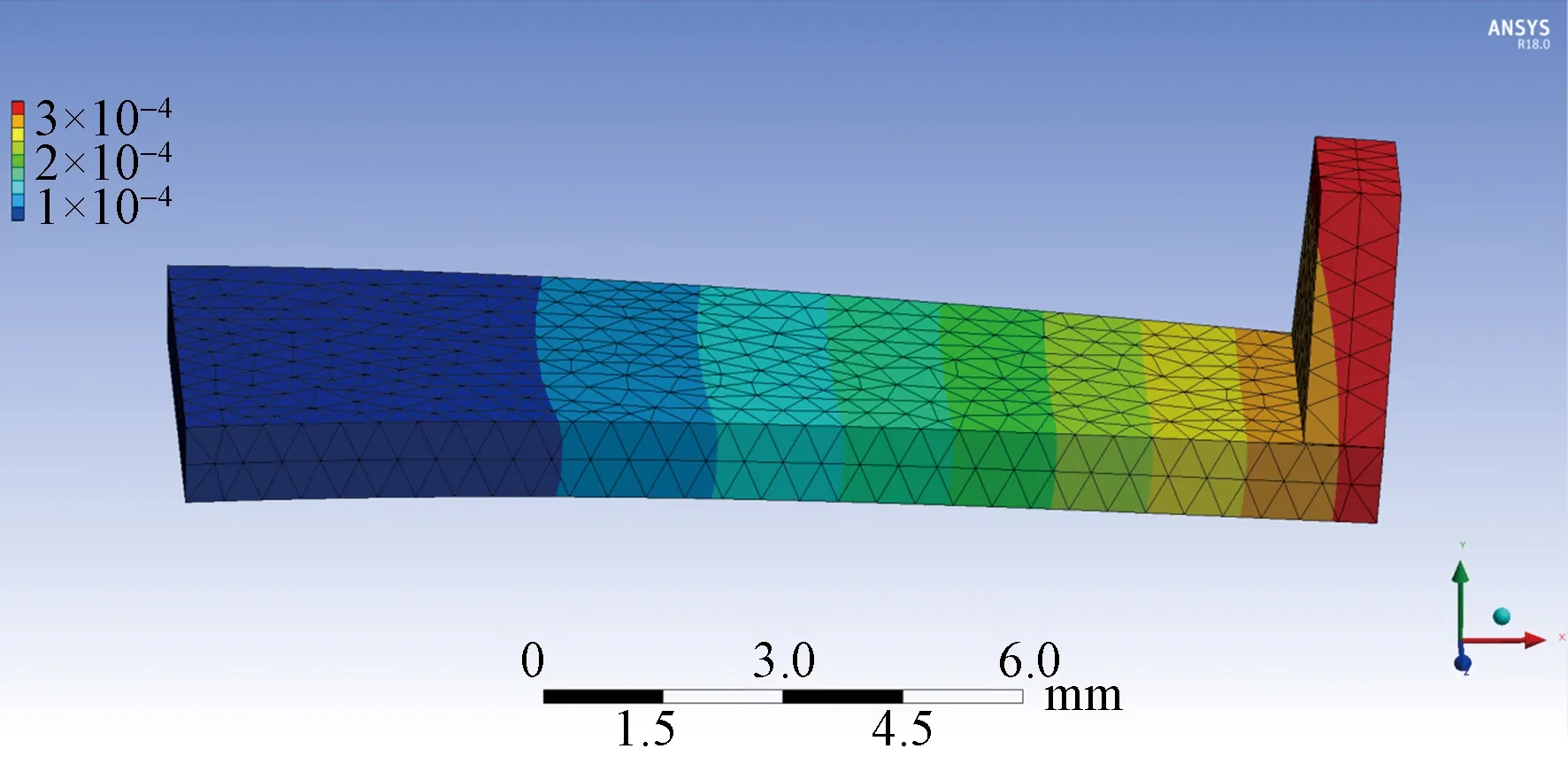
圖4 應變云圖Fig. 4 Strain nephogram

為得到懸臂梁的固有頻率,對懸臂梁進行一階模態分析,如圖5所示。

圖5 一階模態分析Fig. 5 First order modal analysis

可知,結構的一階固有頻率為105 kHz,遠遠大于紗線正常工作的頻率(2.6 kHz),可正常響應紗線振動的頻率,但因紗線張力頻譜豐富,由于諧振導致傳感器信號包含此頻率的可能性較大,所以在信號處理過程中必須進行濾除。

2.4 傳感器傳遞函數

根據傳感器三角結構,可推導出懸臂梁自由端垂直作用力f的大小,懸臂梁雙面粘貼電阻應變片,布局如圖6所示,通過應變分析,可獲得傳感器上作用力和電阻變化量的函數關系。

圖6 懸臂梁受力圖Fig. 6 Stress diagram of cantilever beam

懸臂梁表面應變為

(5)

式中:M為彎曲力矩,N·m;Z為斷面系數,cm3;E為彈性系數,Pa。彎曲力矩M和斷面系數Z為

M=Fl′

(6)

(7)

式中:F為懸臂梁作用力,cN;l′為末端到應變片的距離,cm。

應變片兩端的x為力到應變片的位置,cm;x1為應變片長度,cm;應變分別為

(8)

(9)

根據應變片的電阻特性可知:

ΔR=KsεR0

(10)

式中:ΔR為應變片電阻變化量,Ω;Ks為應變片應率;R0為應變片阻值,Ω。由式(8)～(10)可知,懸臂梁應變片電阻R與力F的傳遞函數為

(11)

2.5 傳感器輸出信號特征和濾波方法

傳感器懸臂梁結構中電阻應變片將紗線張力信號轉換為電壓信號,在高速無縫內衣機高達 2.6 kHz 頻率下應變片輸出信號的時域和頻域結果如圖7所示。

由圖7(a)可知,信號會出現突變峰值,這與紗線張力變化特征不符合,屬于信號奇異點,考慮軟件濾除。由圖7(b)可知,信號中包含了紗線正常波動信號和其它干擾信號。其中,超出正常波動頻率的屬于高頻干擾,低于正常波動頻率的屬于低頻干擾。

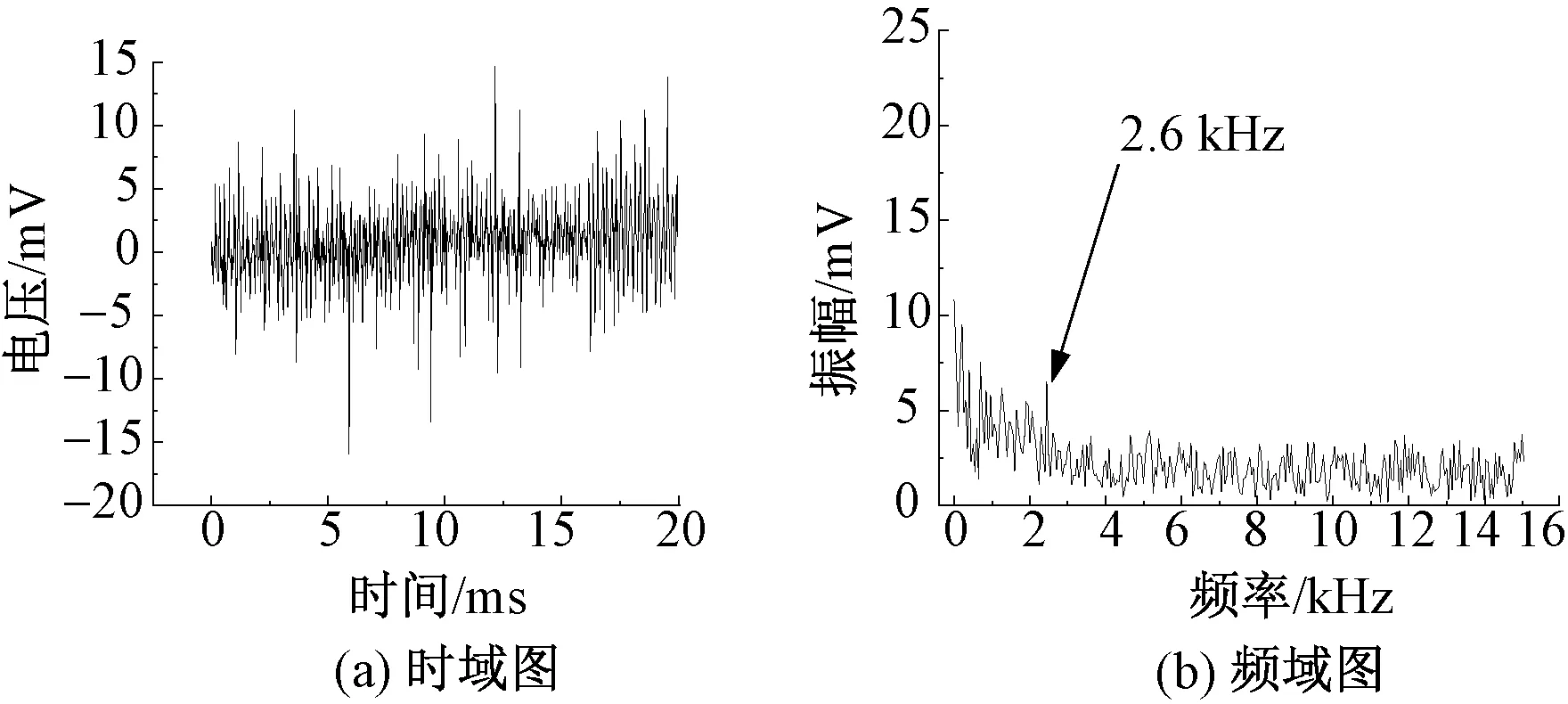
圖7 紗線張力波動信號圖Fig. 7 Diagram of yarn tension fluctuation. (a)Waveform; (b)Spectrum

針對以上3種不同無效信號的特征,根據難度依次采用限幅濾波、低通濾波和S-G卷積算法進行處理。

2.6 電路設計

由于電阻應變片本身材質和結構限制,輸出信號的變化量處于毫伏級,易被噪聲掩蓋,因此,在信號模數轉換前需進行放大處理。所設計的放大電路既要實現電路的高增益,又要增強電路的抑噪能力,因此設計出閉環增益放大電路如圖 8所示。閉環增益放大電路由雙臂平衡電橋和三級儀表放大電路組成。其中:R1、R4、R10、R11組成雙橋電路;R6、R8組成調節平衡電路;A1和A3運算放大器目的是緩沖輸入電壓,提高增益;A2與R5、R7、R9組成放大電路,其中令R5=R9,R2=R12,R3=R13,則放大電路輸出結果Vout為

(12)

式中:V為電壓值,V;R為電阻,Ω。

圖8 閉環增益放大電路圖Fig. 8 Diagram of closed loop gain amplifier circuit

3 數據處理

由上文可知,紗線張力測量結果中存在3種噪聲干擾信號:奇異點噪聲、高頻噪聲和低頻耦合信號,3種信號中奇異點噪聲與張力信號在時域和頻域上都不相同,所以可直接去除;高頻信號在頻域上與張力信號互不關聯,所以在頻域上也可直接將高頻噪聲信號去除;低頻耦合信號與實際張力信號相互耦合無法直接去除,所以采用S-G卷積平滑的方式進行處理,考慮到S-G算法擬合效果受曲線波動情況影響,所以需要按照限幅濾波、低通濾波和S-G卷積平滑的順序進行處理。

3.1 濾波處理算法

3.1.1 奇異點干擾

針對圖7中的信號奇異點干擾,設計限幅濾波算法,去除非周期的不確定干擾信號。通過比較相鄰2個時刻xk和xk-1的采樣值,根據信號變化特征估計2次采樣的最大允許值,如果2次采樣的差值大于最大允許值,則認為發生了隨機干擾,將后一次的采樣值刪除并用上一次采樣值代替,否則,認為本次采樣值有效。

假設采樣k次,采樣值分別為x1,x2,…,xk-1,xk,2次采樣值的差值為A,可知:

(13)

3.1.2 高頻噪聲

針對圖7中的高頻噪聲信號,設計低通濾波器以實現濾除高頻噪聲的功能[12]。低通濾波是一種過濾方式,規則為低頻信號能正常通過,超過臨界值的高頻信號則被阻隔、減弱。假設α為濾波系數,X(n)為本次采樣值,Y(n-1)為上次輸出值,Y(n-1) 為本次濾波輸出值,則濾波公式為

Y(n)=αX(n)+(1-α)Y(n-1)

(14)

3.2 S-G卷積平滑算法

圖7中的低頻噪聲與有效信號相耦合的信號,很難直接解耦去除,為最大程度地保留其中的有效信號,濾除干擾,設計基于S-G卷積的平滑算法,對已去除奇異點和高頻噪聲的信號進行平滑處理。 S-G卷積平滑是基于最小二乘法,利用多項式進行數據處理,可保留信號中的有用信息并消除噪聲,最直接的結果就是將數據的“毛刺”去掉,使數據更加平滑。S-G卷積平滑算法的關鍵在于矩陣算子的求解,設窗寬為n=2m+1,各測量點為x=(-m,-m+1, …,-1,0,1,…,m-1,m),那么采用k-1次多項式對窗口內的數據點進行擬合可得:

y=a0+a1X+a2X2+…+a1Xk-1

(15)

同理可以得到n組方程,構成k元線性方程組,在n>k的情況下方程有解,通過最小二乘法確定擬合參數B,用矩陣表示為

Y(2m+1)×1=X(2m+1)×k·Bk×1+E(2m+1)×1

(16)

則A的最小二乘解A′為

A′=(XT·X)-1·Y

(17)

可得Y的模型預測值為

Y′=X·B=X·(XT·X)-1·XT·Y

(18)

S-G卷積平滑算法是一種根據實際數據波形進行寬度調整的窗函數,窗寬不同會導致不同的效果,參數過窄會使波形不夠平滑,參數過寬又會有較大的滯后性。通過采集模仿織機工作時紗線的正弦振動信號,并進行不同程度卷積處理,圖 9示出原始數據經高、中、低卷積處理后的波形。

由圖9可以發現,通過中等程度卷積效果處理的波形更接近激勵信號的實際情況,低等卷積雖然可以擬合出光滑的曲線,但是周期幅值相差較大,高等卷積擬合效果會失去部分真實信息。

圖9 振動信號測試曲線Fig. 9 Curves of vibration signal test

3.3 軟件濾波嵌入式編程實現

織物編織過程往往有多路紗線參與,多路紗線張力測量的實時性和同步性要求較高,為適應工程應用要求,數據處理部分在嵌入式高性能處理器內實現。圖 10示出主程序流程圖,應變片信號經放大處理后,使用A/D轉換模塊進行數據采集,再對原始數據進行限幅濾波、低通濾波、卷積處理等。

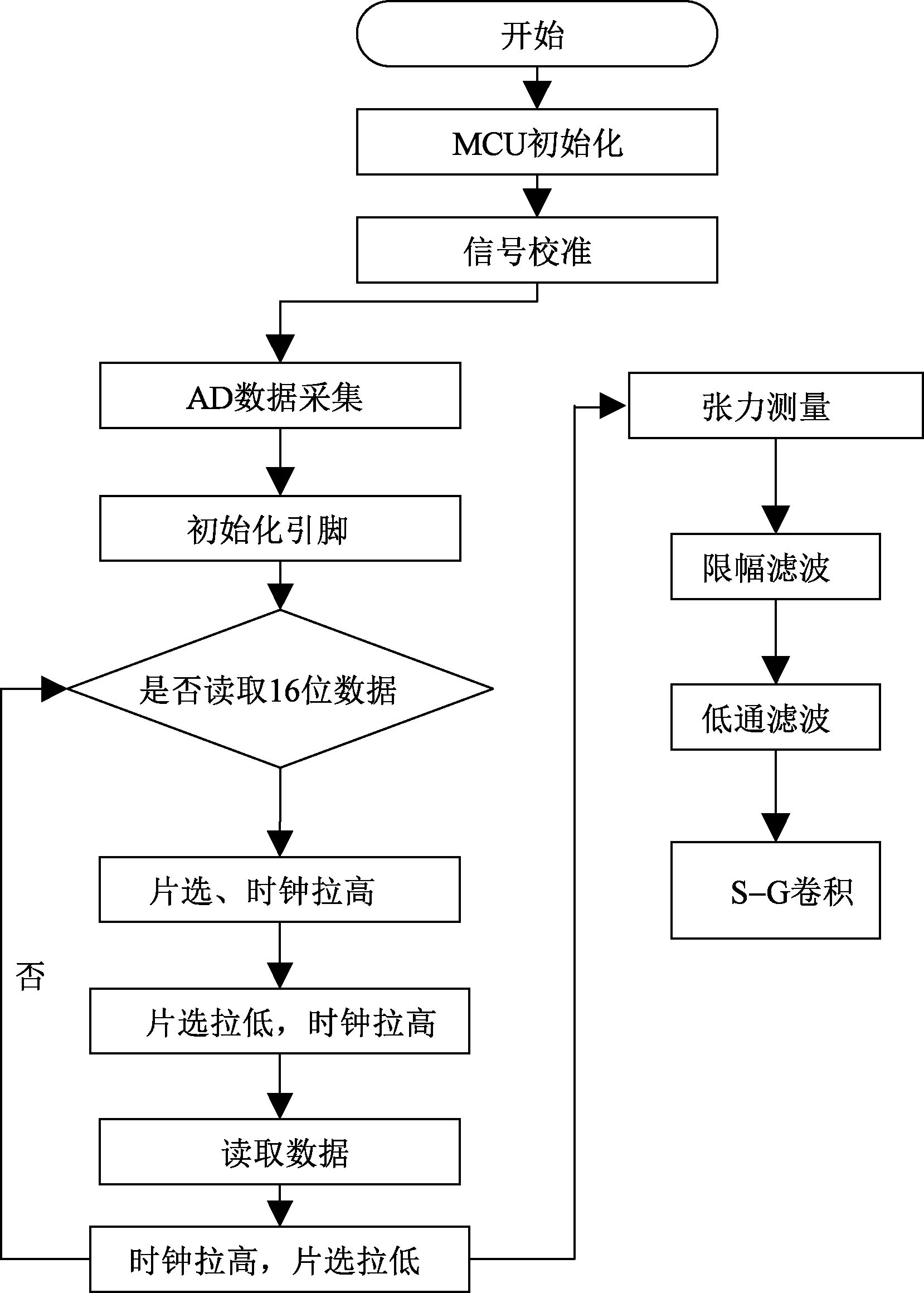
圖10 軟件工作流程圖Fig. 10 Diagram of software workflow

4 紗線張力測量實驗

4.1 實驗平臺搭建

為驗證基于卷積濾波算法紗線張力測量方法的可行性,根據高速無縫內衣機送紗原理搭建了紗線張力測試實驗平臺,其簡圖如11所示。實驗平臺由輸紗器、張力傳感器、勾針和槽筒組成,紗線從筒紗退繞,經輸紗器輸送,穿過張力傳感器和勾針,槽桶帶動紗筒對紗線進行卷繞。其中,輸紗器用來紗線輸送以及將檢測紗線的張力值作為本文設計紗線張力實時測量數據的對照組,勾針模仿高速無縫內衣機工作時的動作對紗線產生激勵。

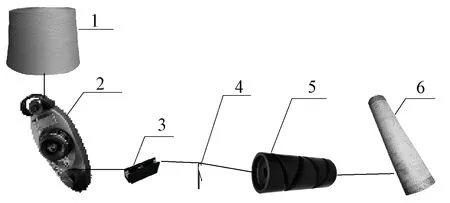
1-紗線;2-輸紗器;3-張力傳感器;4-勾針;5-槽筒;6-紗筒。圖11 實驗平臺簡圖Fig. 11 Block diagram of experimental platform

4.2 傳感器靜態特性標定

為獲得測量數據和紗線張力值的對應關系,對張力測量系統進行靜態標定如圖12所示。將紗線一端固定傳感器受力處,另一端經導紗軌懸掛不同質量的砝碼,靜置后記錄電壓值和砝碼值,重復10次實驗,去除最大、最小值后取平均值作為靜態標定結果。

圖12 靜態標定Fig. 12 Static calibration

傳感器標定結果如圖13所示。利用SPSS對標定結果進行線性回歸擬合分析得出:二者線性相關性為0.928,方差分析的顯著性值為0.000,二者線性關系系數K=0.019,b=0.924 47。

圖13 靜態標定擬合Fig. 13 Static calibration fitting

張力為F,電壓為V,則V與F關系為

V=0.019F+0.924 47

(19)

4.3 濾波處理

用SPSS軟件對動態采樣數據進行概率統計和正態分布擬合,結果如圖14所示,其均值μ為38.6 cN,方差σ為2.51。

圖14 概率統計直方圖Fig. 14 Probability statistics histogram

將方差σ作為奇異點閾值代入式(14)中發現,可以去除大多數奇異點,結果如圖15所示。

圖15 限幅濾波圖Fig. 15 Diagram of amplitude limiting filter. (a)Waveform;(b)Spectrum

為去除高頻噪聲,在頻域上設定2.6 kHz為閾值去除高頻噪聲。通過低通濾波器對奇異點去除后的數據進行處理,得到張力波形和頻譜圖,如圖 16所示,在時域上和頻域上的高頻噪聲均被過濾。

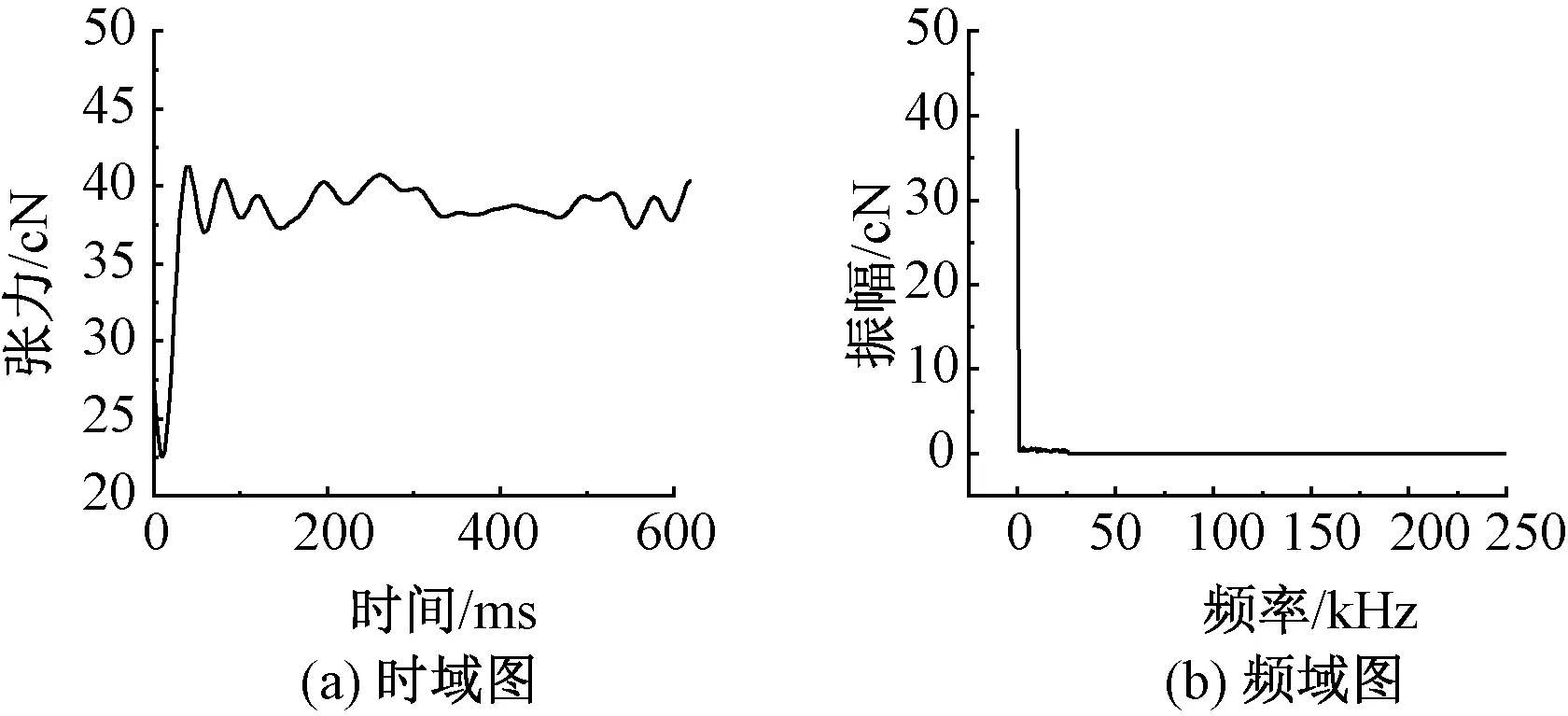
圖16 低通濾波Fig. 16 Diagram of low pass filtering.(a) Waveform; (b)Spectrum

4.4 卷積處理

為驗證S-G卷積濾波算法的平滑效果,將德國高精度TENSOMETRIC張力傳感器采集的紗線張力作為標準數據和本課題設計的傳感器數據做對比圖,結果如圖 17所示。

圖17 數據擬合對比Fig. 17 Comparison of fitting data

數據表明:標準數據中的紗線張力平均值為38.73 cN,標準差為0.27;濾波卷積擬合出的紗線張力平均值為38.5 cN,標準差為0.51。利用卷積算法得出的紗線張力和TENSOMETRIC張力傳感器測量的張力誤差在0.6%以內,標準差在0.62%以內。

4.5 紗線變張力實驗

為進一步驗證該算法的準確性和有效性,控制平臺的輸紗器,將紗線張力從36 cN突變到42 cN, 使用TENSOMETRIC張力傳感器和本課題設計的傳感器對張力波動進行實時測試,結果如圖 18所示。實際測量紗線張力符合突變規律,并且本文方法擬合出的紗線突變張力優于標準傳感器擬合的張力。

圖18 實際張力測試和擬合結果Fig. 18 Actual tension test and fitting results

5 結束語

本文利用懸臂梁結構、濾波和卷積算法,提出了一種基于卷積濾波算法的接觸式紗線張力檢測方法。首先,根據高速無縫內衣機紗線波動特征,結合懸臂梁結構特點確定紗線張力傳感器優化方法。然后,對采集到的數據進行限幅濾波、低通濾波和S-G卷積算法進行處理。最后,通過實驗將測量結果與TENSOMETRIC張力傳感器測量的結果進行對比,張力誤差在0.6%以內,標準差在0.62%以內。并且,該方法對紗線突變張力的檢測有較好的適用性,可將獲取的處于波動狀態的紗線張力處理成穩定的張力輸出,供紗線張力調節系統使用,能夠滿足復雜工作環境下紗線張力的實時測量。