內孤立波在密度連續變化數值水槽中的模擬方法研究*

楊永春, 董崇政, 郭春龍

(中國海洋大學工程學院, 山東 青島 266100)

內孤立波是發生在海洋密度躍層中的非線性波動,振幅可達上百米、流速最大可達2 m/s。內孤立波主要形式有單個孤立波、多個孤立波組成波包和多個波包組成波群,其產生需要穩定層化的海水、地形的擾動和動力源[1]。內孤立波經過時可引起強剪切流,對海洋結構物、潛體以及密度躍層附近的管道等造成嚴重威脅。內孤立波在世界各海洋分布廣泛,尤其在我國南海頻發,對南海開發利用有較大影響。隨著計算機技術的發展,使用數值模擬研究內孤立波的方法得到了越來越廣泛的應用。

目前學者們為分析內孤立波和海洋結構物的相互作用所構建的內孤立波數值水槽,通常忽略實際海洋中密度躍層的厚度,并將上下層流體簡化為兩層密度不同的均一流體。文獻[2-4]中使用Fluent軟件,采用速度入口法,以兩層模型定態內孤立波理論解作為邊界條件,在數值水槽入口輸入上下層平均速度和波面位置以構造內孤立波數值水槽,黃文昊等[5]通過水槽實驗分析了各理論的適用條件;文獻[6-7]中使用重力塌陷法,文獻[8-9]中使用推板法,通過模擬內波實驗室的造波過程構造內孤立波數值水槽;尤云祥等[10]使用質量源法研究內孤立波生成機理、傳播及流場特性。以上構造的內孤立波數值水槽均基于兩層模型,李景遠等[11]引入密度輸運方程,模擬了密度連續分層流體中內孤立波的傳播,指出忽略密度躍層的厚度會高估內孤立波的傳播速度。兩層模型上下層最大流速均出現在流體分界面處,與實測數據存在差異,進而可能誤估其載荷,因此有必要建立密度連續變化內孤立波數值水槽。構建密度連化變化數值水槽的關鍵在于確定數值水槽的密度分布形式和與之相應的邊界條件。

物理海洋中對于內波問題的研究十分廣泛,積累了大量的觀測資料和數值模擬方法,建立了大量可用于分析密度連續層化內孤立波的計算模型。麻省理工學院通用環流模式(MIT general circulation model,MITgcm)是大氣海洋的通用數值計算模型,采用有限體積法離散N-S方程,可計算完全非靜壓項,在內孤立波研究中得到了廣泛的應用。Legg等[12]使用MITgcm對潮流經過高斯地形后產生的內潮現象進行了研究,文獻[13-18]中使用MITgcm對中國南海的內孤立波生成及傳播演化規律進行了研究。蔡樹群[19]將內孤立波計算模型的結果與莫里森公式結合計算了內孤立波對圓形樁柱的載荷。MITgcm模擬得到的內孤立波數據能夠與觀測數據趨勢吻合,但MITgcm無直接分析內孤立波與海洋結構物相互作用的功能。

本文提出將MITgcm與Fluent相結合的方法構造密度連續變化內孤立波數值水槽。以潮流經過高斯地形產生的內孤立波為例,通過MITgcm構建二維數值模型,使用南海北部物理海洋數據,由潮地作用生成內孤立波,將Fluent數值水槽置于MITgcm計算域內,提取MITgcm對應位置處的結果數據,利用用戶自定義函數(User defined function,UDF)對Fluent數值水槽進行初始化并將入口對應位置的結果數據作為邊界條件,通過兩側的速度入口邊界使內孤立波進入數值水槽中,在數值水槽與MITgcm計算域的相同位置處可以形成基本一致的內孤立波。本文提供了研究連續層化模型下內孤立波與海洋結構物相互作用的數值造波方法。

1 模擬方法

1.1 MITgcm設置及計算結果

本文首先在MITgcm中生成內孤立波,建立二維模型,坐標系x軸放在海平面上。地形設置為高斯型海山模型,海底坐標形式為:

z=-H0+h0·exp(-x2/(2L2))。

式中:總水深H0=500 m;海山高h0=230 m;設置山脊寬度L=15 km。模式水平計算域設置為500 km,水平長度足夠大,使得生成的內孤立波不會到達邊界。水平方向網格尺寸為250 m,垂向共分為50層,層厚10 m。將模式時間步長設為10 s以滿足柯朗-弗里德里希斯-列維(Courant-Friedrichs-Lewy,CFL)條件,共模擬4個太陽主要半日分潮(M2潮)周期。模式初始條件為水平均勻,層化數據選自海洋世界地圖(World Ocean Atlas 2018,WOA18)數據集,取南海北部夏季的平均溫度和平均鹽度(見圖1), 將其平均值插值到垂向網格點上。本文取AH=KH=1×10-4(單位:m2/s),AZ=KZ=0 (單位:m2/s),采用Pacanowski和Philander[20](PP81)混合方案作為參數化方案。開邊界采用M2潮流驅動,設置潮流振幅U0分為0.55、0.65、0.75、0.85和1 m/s的五種工況。為了防止在開邊界處發生反射,采用海綿邊界進行消波,海綿層設置寬度為15 km。模式使用剛蓋邊界條件,忽略內孤立波與海表面的相互作用,在底部使用自由滑移邊界條件。

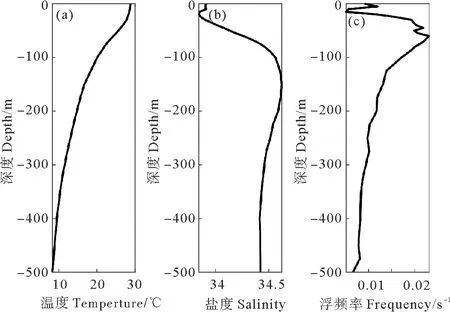
圖1 模式初始溫度(a)、鹽度(b)及對應浮性頻率(c)的垂向結構

如圖2所示,以U0=0.65 m/s的工況為例,在2.75個M2潮周期時,潮流向右,在海山處等密線出現大幅凹陷;在3個M2潮周期時,在50 km處出現大幅的內孤立波;在3.25個M2潮周期時,潮流轉為向左,內孤立波傳播至70 km處,并進一步演化為內孤立波列。同時,可見上一潮周期生成的內孤立波列從100 km處傳播至140 km處,相速度約為1.73 m/s,在傳播過程中受到潮流影響,振幅先增大后減小,波包中各內孤立波的間距先增大后減小。在不同潮流振幅下,M2潮均與地形相互作用激起內孤立波,當潮流與內孤立波傳播方向一致時內孤立波流速增大,方向相反時流速減小。潮流振幅越大,內孤立波振幅越大,背景潮流對內孤立波流速的影響也越大。

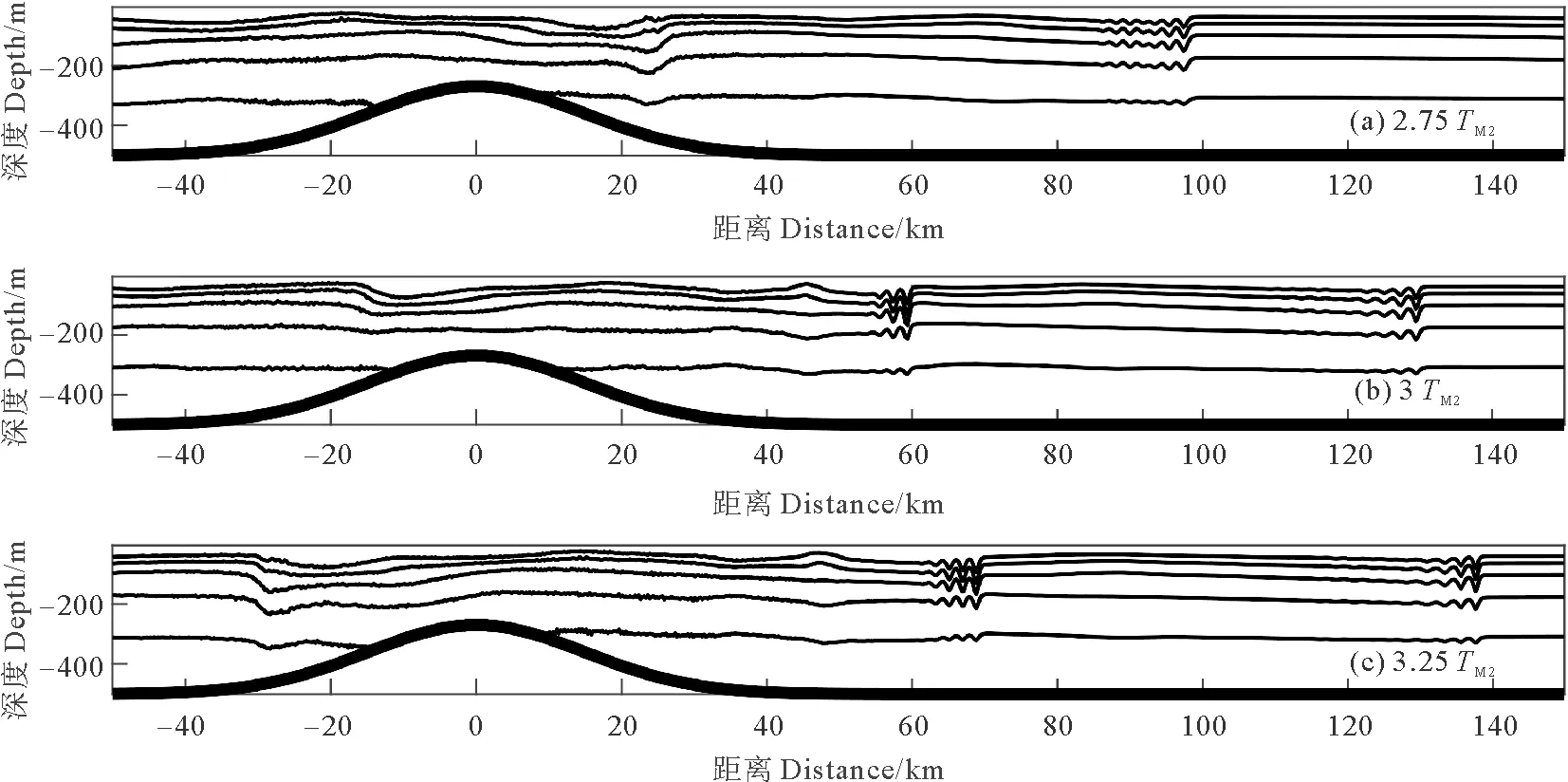
(起始時刻 Start time: U0 =0.65 m/s; TM2: M2潮周期 Period of M2.)

Fluent數值水槽的左側邊界設置在MITgcm計算域121 km處,右側邊界設置在計算域126 km處,內孤立波數值水槽總長5 000 m,如圖3紅框所示。各工況基本設置一致,僅初始化條件不同,以U0=0.65 m/s工況的銜接初始時刻為例(見圖3)進行說明。在第3個M2潮周期時,由潮地作用生成的內孤立波波包的頭波到達數值水槽左側邊界,以此刻作為Fluent數值水槽計算的起始時刻,以1 200 s作為終止時刻,以使得內孤立波可以完全進入數值水槽中。起始時刻數值水槽內部水平流速在靠近海表面處為正向,靠近海底處為反向,最大流速約0.2 m/s,等密線水平變化較小。各工況數值水槽起始時刻的流速場和密度場均受到背景潮流的影響,與兩層模型靜止穩定的初始條件明顯不同。

1.2 Fluent設置

在Fluent軟件中建立水平向5 000 m,垂向500 m的數值水槽,坐標系放在海平面上,以左側邊界為X軸起點。水平網格尺寸取為內孤立波特征長度的十五分之一,垂向網格尺寸在浮力頻率最大處做加密處理。

采用流體體積(Volume of fluid,VOF)法模擬密度連續變化的水體,通過求解每一相流體的體積分數來確定每一控制體的密度大小。設置第一相流體密度為1 020 kg/m3,第二相流體密度為1 030 kg/m3,兩者動力黏度均為1.003×10-3kg/(m·s)。由于內孤立波的流線曲率較大,本文選取RNGk-ε型湍流模型。

數值水槽的上、下邊界條件均取為固壁邊界條件,左、右兩側取為速度入口邊界條件。提取MITgcm計算結果中對應數值水槽邊界處的密度和速度時程數據,編寫UDF文件,將時程數據導入到數值水槽兩側邊界。

以U0=0.65 m/s工況的數值水槽左側邊界為例,在MITgcm計算結果對應位置處的密度和水平速度時程數據如圖4所示。在銜接620 s左右時,內孤立波波谷到達數值水槽左側邊界,內孤立波上層水平流速方向向右,與內孤立波傳播方向一致,最大流速達0.8 m/s,下層流速方向向左,與內孤立波傳播方向相反,達-0.25 m/s,等密線達到最大振幅約48.9 m。

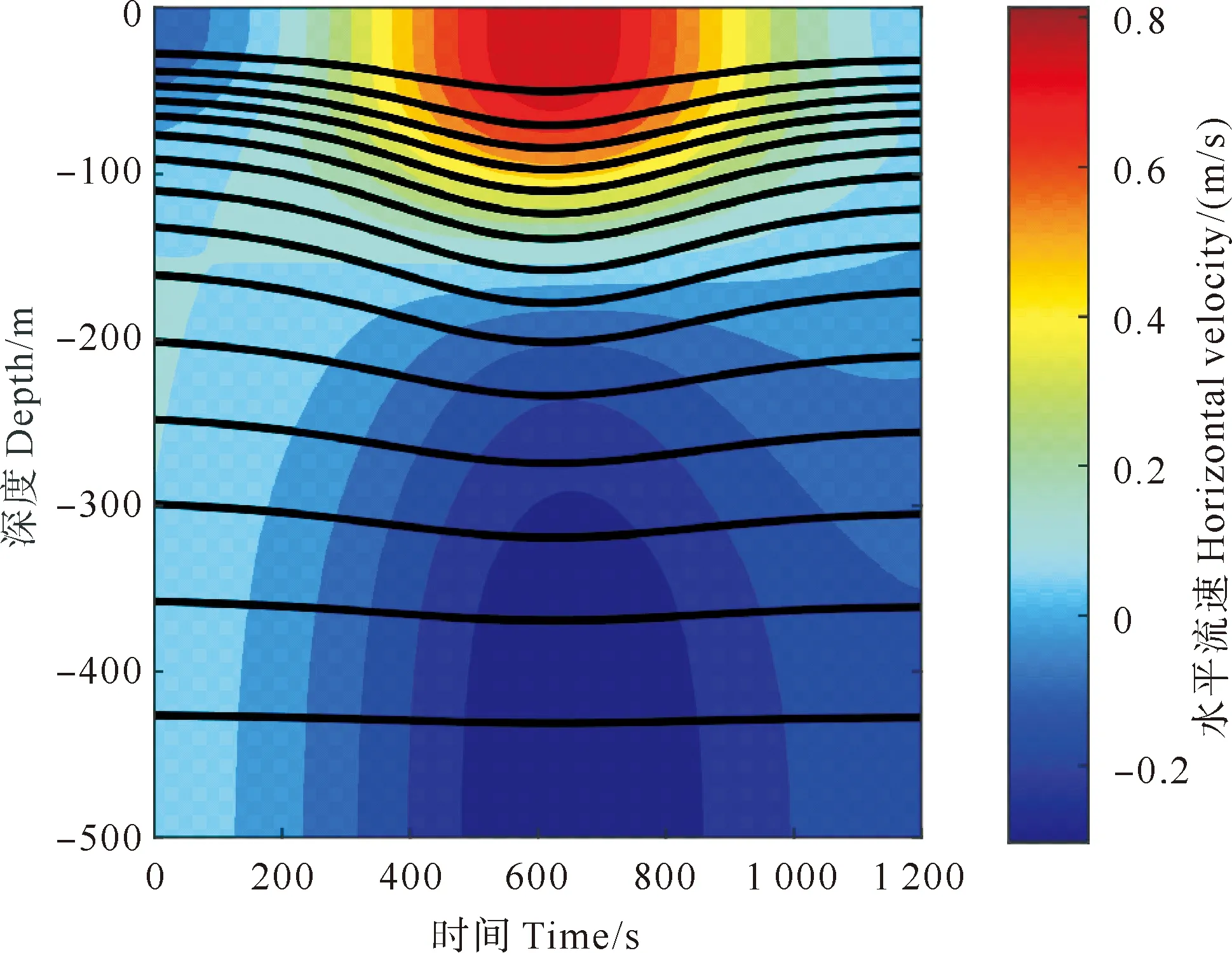
(黑線表示等密度線。Black lines mean density. U0=0.65 m/s )

在計算開始前,需將MITgcm計算域中的流場信息作為初始條件設置在Fluent中。選擇基于壓力的二階隱式時間離散的瞬態求解器,壓力速度耦合方式使用PISO,壓力插值選擇體積力加權法,對流項及輸運方程采用一階迎風格式進行離散。迭代時間步長取0.5 s,為保證計算精度,每個時間步內最大迭代次數30次。

2 結果分析

2.1 等密度線振幅

以U0=0.65 m/s的工況為例,銜接計算結束時等密度線對比如圖5所示。內孤立波傳播至距左側入口約1 000 m處,相速度約1.68 m/s,最大振幅50.21 m。等密度線在水深小于200 m時,Fluent計算結果與MITgcm計算結果吻合度高,水深大于200 m時,Fluent計算的振幅略大于而MITgcm計算的振幅。在各工況中均出現此現象,原因在于兩者對密度的處理方法不同,MITgcm使用海水狀態方程計算密度,考慮到密度受壓強影響,而Fluent使用不可壓縮假設,在深水中密度隨水深變化緩慢,浮力頻率小,兩者差異明顯。

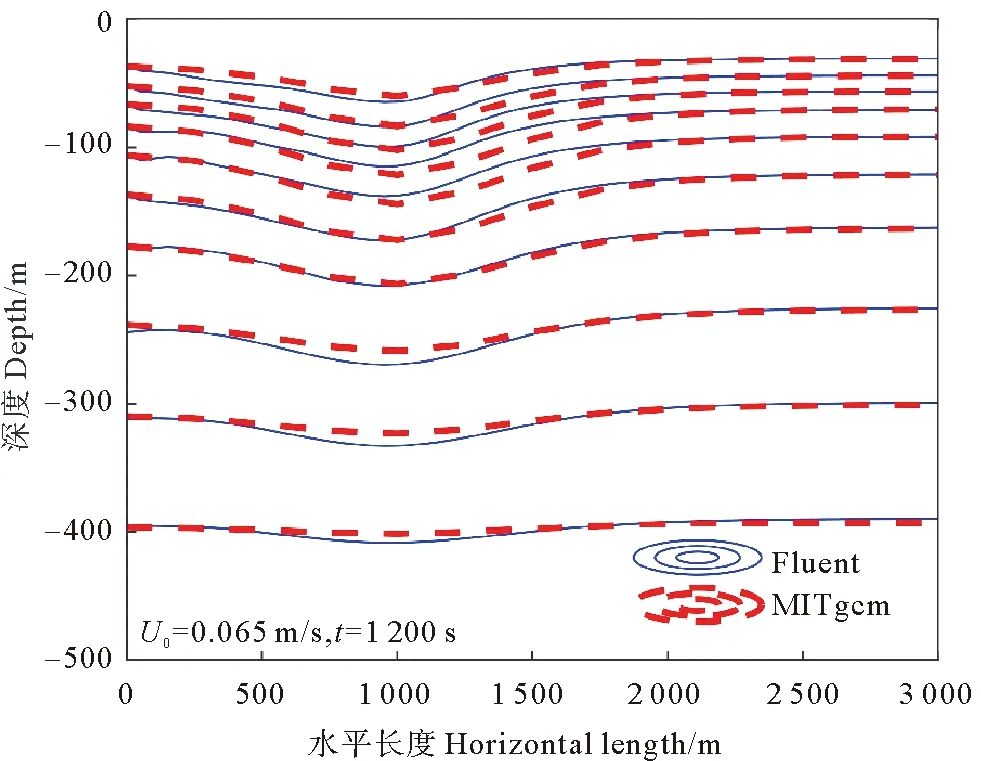
圖5 密度模擬結果對比

提取各工況1 025.5 kg/m3等密度線在距入口250 和500 m處的時程數據,對比如圖6所示。各工況中波谷到達時間不同,這是由于不同工況下開始銜接時內孤立波距入口的位置有差異,并且各工況內孤立波傳播速度也有差異導致的。在各工況中,Fluent計算結果均能同MITgcm計算結果吻合,總體偏差較小。

將等密度線最低深度與初始深度之差作為振幅,統計各工況1 025.5 kg/m3等密度線振幅如表1所示。可見隨著潮流振幅增加,內孤立波振幅基本增大。在內孤立波由距入口250 m傳播至距入口500 m的過程中,內孤立波振幅也在演變,呈增大趨勢。在各工況中,數值水槽與MITgcm計算域的相同位置處的內孤立波振幅偏差小。

表1 1 025.5 kg/m3等密線振幅數據

2.2 水平流速

統計各工況在距入口250和500 m處, 水深70、150、250 m處水平速度時程計算結果(見圖7)。當內孤立波到達時各水深水平流速同時到達最值,水深70和150 m處流速相反,可形成較大的水平流速垂向剪切作用。在水深150 m附近的水平流速在全時程中始終變化不大。

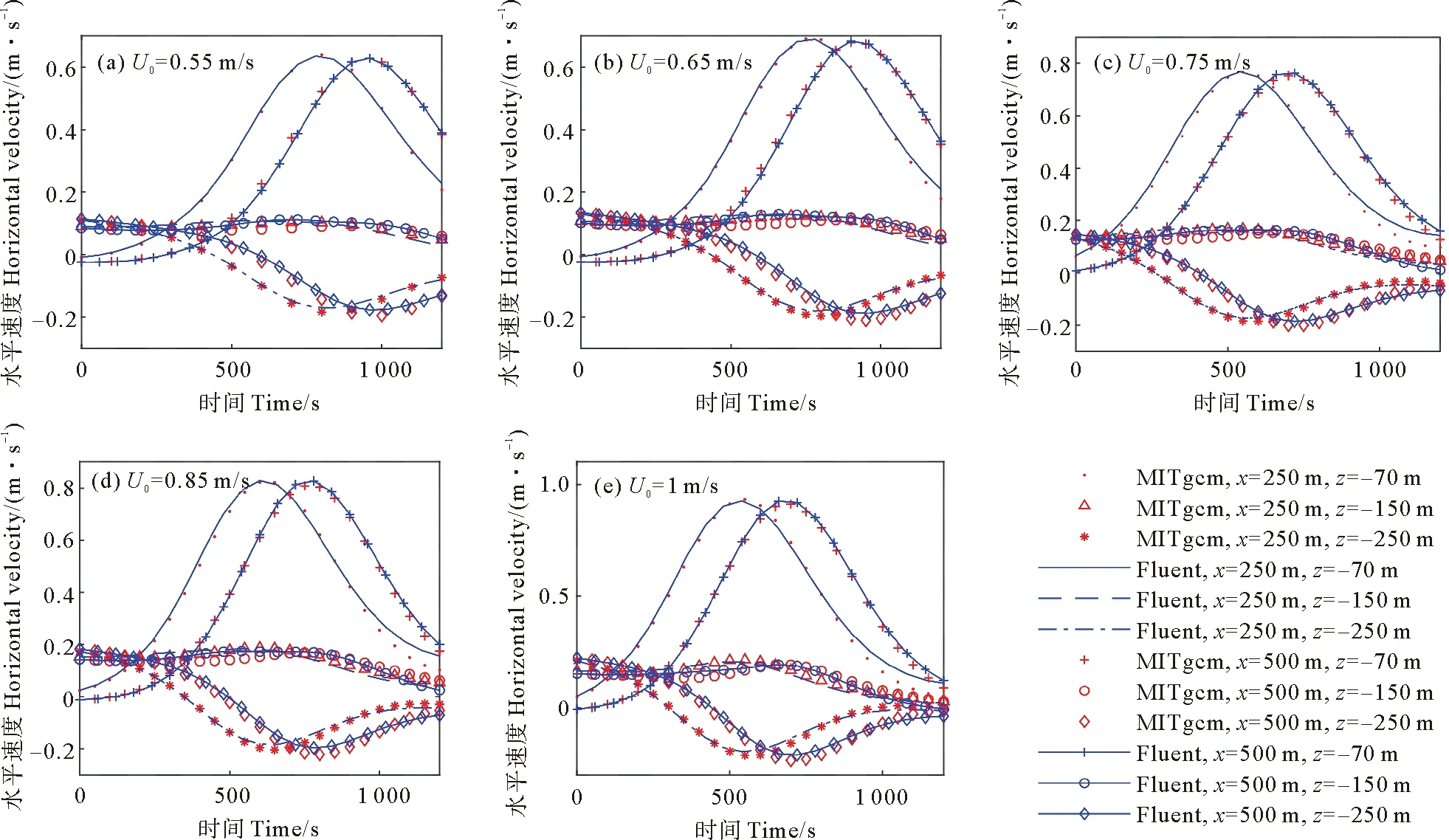
圖7 水平速度時程數據

以U0=0.75 m/s工況為例(見圖7(c))。在初始時刻,水深70 m處流速接近零,水深150和250 m處流速向右,最大不超過0.18 m/s。隨著內孤立波到來,上層流速方向轉為向右,最大達0.76 m/s,下層流速方向轉為向左,達-0.18 m/s。Fluent計算結果能夠較好地反映出MITgcm計算結果中水平流速的時程變化,僅水深70 m處在內孤立波經過后水平流速有最大0.05 m/s的偏差。

圖7(a)—(e)對比分析可知,隨著潮流振幅U0的增加,在水深70 m附近的最大水平流速增加,但在水深250 m附近的最大水平流速基本不變。在各工況各水深中,Fluent計算結果與MITgcm計算結果吻合。

2.3 兩層模型

以U0=0.65 m/s工況為例對比兩層模型理論結果。提取Fluent數值水槽的浮頻率分布,以最大浮頻率和最小浮頻率的平均值所在深度為密度躍層的上、下位置,取密度躍層下層位置為兩層模型的分界面,可得上層水深120 m,平均密度1 022.1 kg/m3,下層水深380 m,平均密度1 027.6 kg/m3。理論解振幅取對應深度處等密度線振幅為-49.8 m。

在距入口250 m處波面對比結果如圖8所示。內孤立波波谷在銜接至760 s時到達距入口250 m處,兩層模型的各理論波面均與MITgcm的計算結果有偏差。Korteweg de Vries(KdV)理論波長最短,波形最為陡峭,拓展的KdV(Extended KdV,eKdV)理論和Miyata-Choi-Camassa(MCC)理論波長稍寬,波形也較為平緩。與兩層模型結果對比,MITgcm計算結果所得的波形更為平緩,并且在內孤立波經過后出現波面下降的現象,兩側并不對稱。在各理論中,MCC理論結果與MITgcm計算結果最為接近。Fluent計算結果在波谷到達前能夠與MITgcm結果吻合,在波谷到達后出現偏差,波面下降更大。

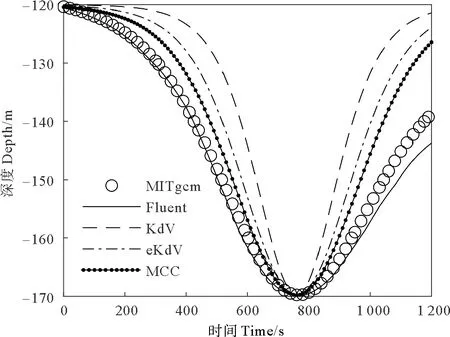
(U0=0.65 m/s,x=250 m)圖8 1 025.5 kg/m3等密線時程數據對比,

水平流速在垂向分布對比結果如圖9所示。兩層模型理論結果與MIT gcm計算結果存在較大偏差,其中MCC理論的偏差最小。在銜接至500 s時,由MCC理論得到的上層水平流速為0.33 m/s,在水深80 m以上均小于MITgcm結果,在水深350 m以下則同MITgcm結果接近。在750 s時,波谷到達距入口250 m附近,由MCC理論得到的上層水平流速達0.73 m/s,與MITgcm在表層處的水平流速相當。在銜接至1 000 s時,內孤立波已經通過距入口250 m處, 由MCC理論得到的上層水平流速回落至0.34 m/s,下層水平流速回落至-0.14 m/s,均與MITgcm計算結果存在較大差異。MCC理論解在兩層流體分界面處存在水平流速迅速變化的躍層,但MITgcm中水平流速不會在某個水深處出現強烈的垂向變化,與實際海洋中內孤立波流速分布規律接近。由MCC理論得到的水平流速同MITgcm計算得到的水平流速在靠近上、下邊界處偏差小,在分界層附近偏差較大。

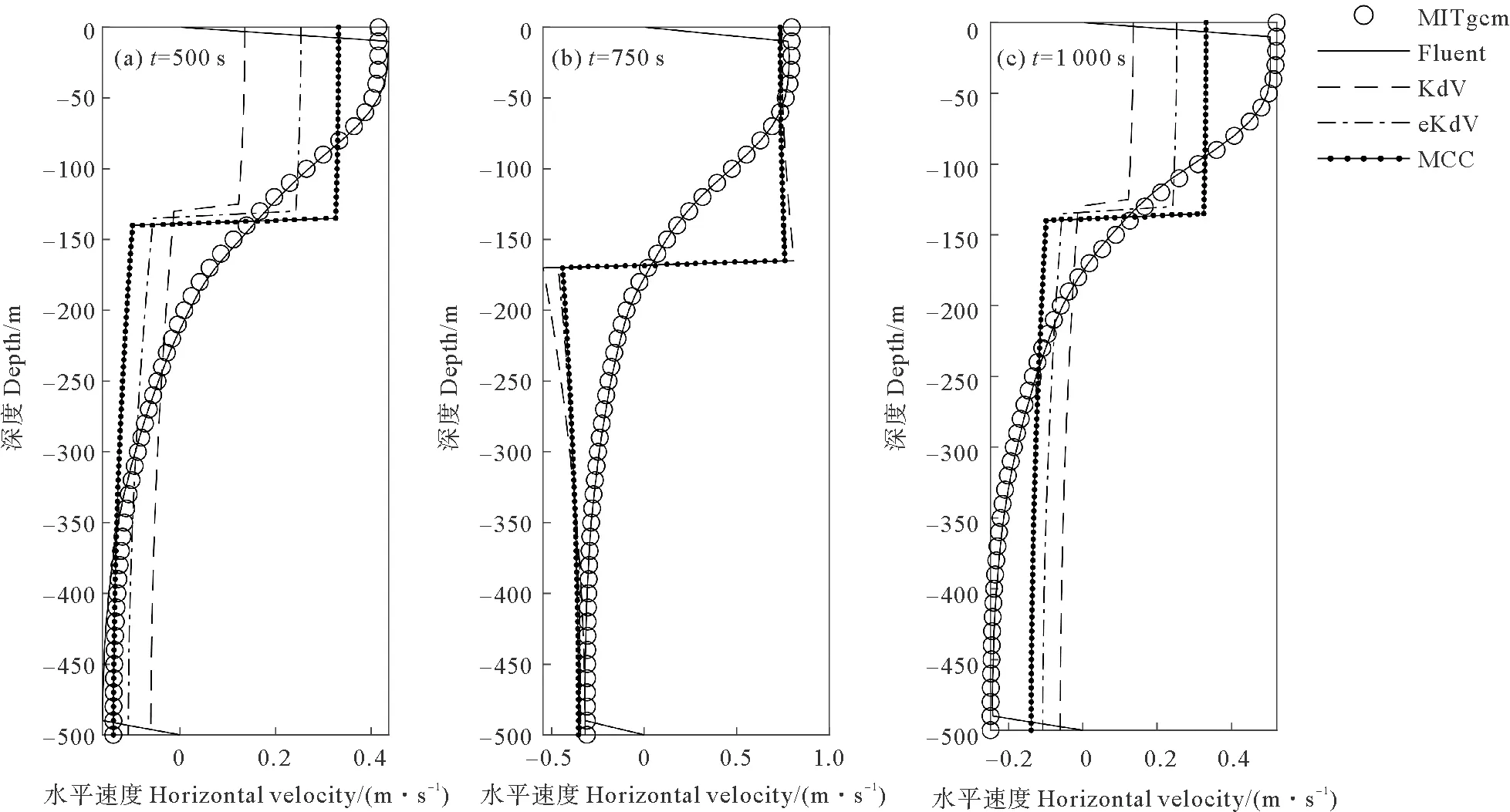
圖9 距入口250 m處不同時刻水平速度垂向分布(U0=0.65 m/s)

數值水槽對水平流速在垂向分布的計算結果可以同各時刻的MITgcm計算結果吻合,僅在上、下邊界處會由于固壁條件差異而出現偏差。

各工況均發現模擬得到的水平流速分布與兩層模型不同,上、下層流速極值并未出現在同一水深。這是由于兩層模型將浮頻率較大的密度躍層厚度忽略,密度在躍層附近迅速變化,導致水平流速在密度躍層處的垂向變化過于劇烈,并且MITgcm水平流速的計算結果受到了背景流影響。

3 結論

(1)本文使用MITgcm生成內孤立波,將Fluent數值水槽置于MITgcm計算域內,提取MITgcm的結果數據對Fluent數值水槽進行初始化并將入口對應MITgcm位置處的結果數據作為邊界條件,實現了兩者的銜接。使用這一模擬方法對給定海域不同潮流振幅下的算例進行計算得到的結果表明:數值水槽中的內孤立波同MITgcm相同位置處的內孤立波水平流速基本一致,且等密度線在密度躍層處偏差小,可以認為在數值水槽中形成了同MITgcm計算域相同位置處對應的內孤立波。本文為內孤立波數值水槽提供了一種確定密度分布形式和邊界條件的模擬方法。

(2)本文中使用MITgcm模擬結果作為邊界條件,而MITgcm可以使用觀測的密度分布形式、潮流和地形生成內孤立波,相較于在數值水槽入口直接使用兩層模型定態內孤立波理論解作為邊界條件,使用范圍更加廣泛。進一步可以借鑒物理海洋中對實際海域的三維數值模擬結果,統計海洋結構物布置地的內孤立波載荷,為分析海洋工程問題提供工具。

(3)算例結果表明,隨著潮流振幅增加,內孤立波振幅和最大水平流速均增大。本文模擬方法得到的內孤立波水平流速垂向分布較為連續,沒有出現兩層模型水平流速在分界面處突變的現象。