氣體超聲換能器動態性能測試方法研究

章圣意,姚海濱,林 恒,卜勤超,趙偉國

(1.浙江蒼南儀表集團股份有限公司,浙江 蒼南 325800;2.上海裕達實業有限公司,上海 200240;3.中國計量大學計量測試工程學院,浙江 杭州 310018)

0 引言

超聲流量計是通過超聲波信號在流體中的信號變化來計算流速的流量儀表,具有低壓損、高精度和寬量程比的特點[1-2]。超聲時差法是目前超聲流量計中應用較為廣泛的方法[2]。然而,超聲波換能器的性能很大程度上決定了超聲流量計的測量精度以及穩定性。因此,準確測量超聲換能器的性能對超聲流量計的性能提升具有重要的意義。

超聲換能器的性能研究可分為穩態性能和動態性能。超聲換能器穩態性能主要為阻抗特性,包括機電耦合系數、機械品質因數和頻率特性等。動態性能主要是超聲換能器在工作狀態下的性能指標,包括靈敏度和波形特征[3]。在穩態性能方面,李家寬等基于虛擬儀器技術設計了新型壓電器件阻抗測試分析系統[4]。陸飛、郭建中等研究了基于計算機控制以及虛擬儀器設計在相位檢測原理下實現的超聲換能器阻抗分析儀的設計[5]。在動態性能方面,陳思從換能器靈敏度和頻率特性等方面分析換能器一致性[6]。其側重于對換能器進行仿真分析。

綜上分析可知,超聲流量計的性能指標與測量中回波信號的特征密切相關。對此,本文提出了1種超聲換能器動態性能測試方法,設計了自動測試系統。該方法采用高斯模型對回波信號進行建模,以獲得回波信號的特征參數,實現對超聲換能器的動態性能評價。

1 測量原理

超聲波回波信號的響應特性不僅與超聲換能器的設計結構(包括背襯、壓電晶體、匹配層等)有關,還與脈沖激勵信號的波形、頻率以及激勵個數有關[7]。

超聲換能器回波波形如圖1所示。

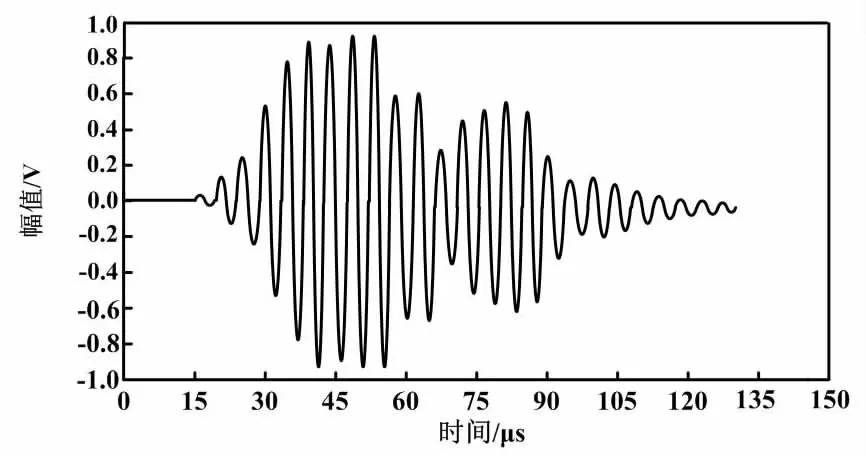
圖1 超聲換能器回波波形

通過回波信號建立的數學模型為:

s(θ,t)=g(θ)u(t)

(1)

式中:s(θ,t)為回波信號,V;θ為特征參數向量,包括回波信號幅值β、帶寬因子α和回波信號中心頻率fc參數;t為時間,s;g(θ)為傳遞函數模型;u(t)為激勵信號,V。

其中:α既反映了回波信號的帶寬范圍,又反映了回波信號在時域中的持續時間;fc與換能器本身的中心頻率以及傳輸路徑的頻率特性有關。

回波特征參數最優解需要以實際回波信號采樣數據與基于高斯模型的回波信號之間的差異大小作為判斷依據。本文引入基于最小二乘法的目標函數式,以求取基于高斯模型的回波信號的最優解。

本文以人工魚群算法搜索回波信號的特征參數,通過目標函數的最小值求取回波信號的最優解。目標函數是采樣回波數據與回波信號模型的平方差[7]。

(2)

式中:x(n)為采集超聲換能器的回波數據,V;N為離散回波采樣點數量;θ(k)為第k次迭代時的回波參數向量估計值;s(θ(k),n)為第k次迭代時的高斯模型,V;f(θ(k))為第k次迭代時的目標函數值,V2。

本文計算θ的歐式距離,并以其作為超聲換能器動態性能的一致性準則。歐式距離計算式為:

(3)

式中:θ1、θ2分別為超聲換能器1、超聲換能器2經歸一化處理后的特征參數向量;d(θ1,θ2)為超聲換能器1、超聲換能器2的歐式距離;θ1i、θ2i為參數向量中的第i個參數向量。

本文由式(3)計算被測超聲換能器之間的歐式距離,并將其作為比較超聲換能器之間動態性能一致性評估的依據。歐式距離越小,則超聲換能器的動態性能一致性越好。

2 回波信號建模

針對回波信號模型的相關研究,常用的數學模型分別為高斯模型[8]和混合指數模型[9]。本文對兩種回波模型進行研究,從而得到最優模型。

高斯模型的換能器回波信號為1個由信號幅值、帶寬因子、到達時間、中心頻率以及相位這4個參數決定其性能的非線性函數[8]。因此,換能器回波信號可由s(θg,t)表示。

s(θg,t)=βe-α(t-τ)2cos[2πfc(t-τ)+φ]

(4)

式中:θg為高斯模型的參數向量,θg=[βατfcφ];τ為回波信號到達時間,s;φ為回波信號初相位,rad,其值一般取0。

高斯模型的參數向量為θg=[1.08 V 0.003 8(kHz)28.9×10-5s 208 kHz 0]。

基于高斯模型的回波信號如圖2所示。

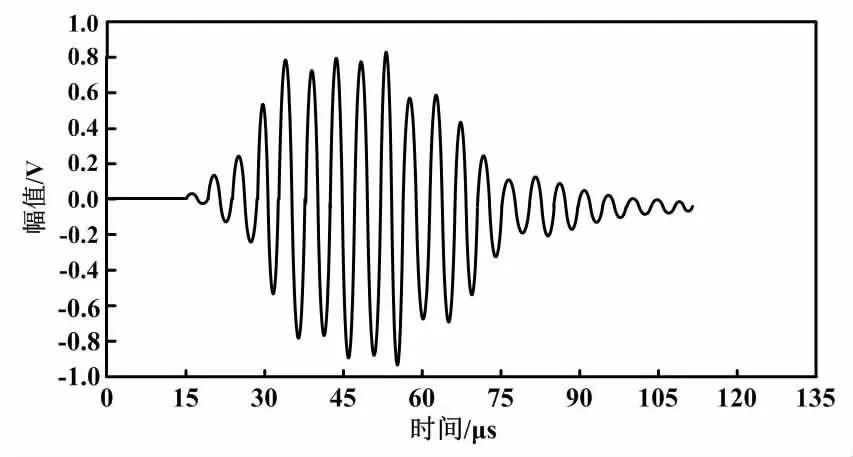
圖2 基于高斯模型的回波信號

由圖2可知,基于高斯模型的回波信號振蕩小波較多且回波峰值上升沿與下降沿的變化速率相近。對比基于高斯模型的回波信號與實際對射回波信號可知,基于高斯模型的回波信號的上升沿部分回波臺階變化與實際波形較為接近,但下降沿部分變化速率過快。

相比于高斯模型混合指數模型的上升沿與下降沿為非對稱變化,高斯模型上升沿部分變化速率較快而下降沿部分變化速率較慢。

混合指數模型表達式為[9]：

(5)

式中:θh為混合指數模型的回波特征參數向量,θh=[βTmτfcφ];m為整數,決定了回波信號能量的集中程度,取值范圍一般為[1,3];T為回波信號的存在時間,s。

回波特征參數向量為θh=[1.0 V 1.3×10-5s 2.0 3.8×10-5s 200 kHz 0]。

基于混合指數模型的回波信號如圖3所示。

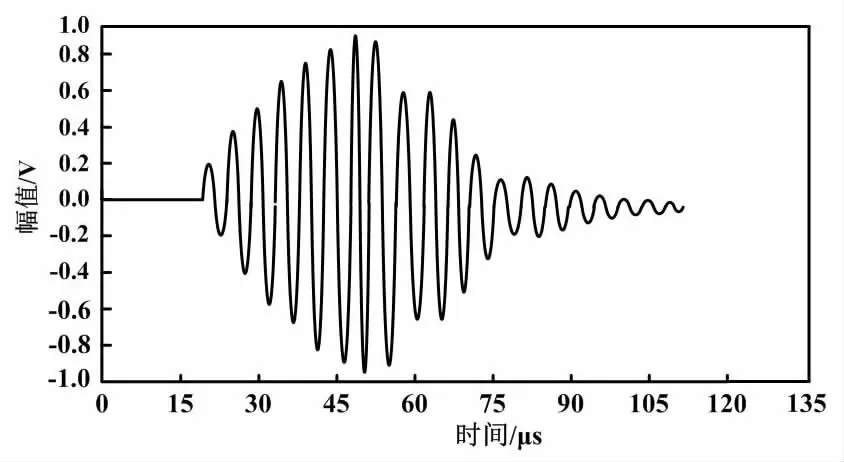
圖3 基于混合指數模型的回波信號

由圖3可知,基于混合指數模型的回波信號在時域上為非對稱信號,回波信號到達時快速振蕩在下降沿部分緩慢衰減。基于混合指數模型的回波信號近似于實際回波信號,但還有一定的差別。這主要是回波信號到達時回波各峰值的幅值變化速度較快,而回波下降沿部分變化則過于緩慢。

從以上對2種模型的仿真回波信號與實際回波信號的分析比較可知,2種模型都不能完全反映實際的回波信號。雖然在上升沿部分都近似于實際的回波信號,但其下降沿都有所差異。結合閾值法測量回波信號到達時間原理,回波上升沿部分的峰值特征用于確定其到達時間,而回波下降沿的波形變化并不影響測量。因此,本文考慮2種模型的仿真回波信號與實際回波信號的上升沿部分的相似度。

為了直觀地量化分析2種模型與實際回波信號的相似程度,以得到回波信號特征參數的最優模型,本文應用最小二乘法構建目標函數。其表達式為:

(6)

式中:f(θ)為目標函數,V2;x(i)為采集得到的實際回波信號,V;s(θ)為2種模型最優估計后的仿真回波信號,V。

本文隨機選取超聲換能器1,采集其對射回波波形,基于高斯模型和混合指數模型分別建立其最優仿真回波信號,并計算2種仿真模型和實際回波信號的差異。通過計算可知,基于高斯模型的回波信號的目標函數值是0.27 V2,遠小于基于混合指數模型的目標函數值0.58 V2。由此可知,高斯模型建立的仿真回波信號更近似于實際的超聲波換能器對射回波信號。因此,本文采用高斯模型建立回波信號的模型。

3 回波特征參數的估計

基于高斯模型的回波信號特征參數向量為θ=[βατfc]。其中,回波信號到達時間τ主要受聲速和環境變化的影響,因此不作為一致性分析的主要特征參數。回波放大電路中的增益值G可代替回波峰值。因此,本文以超聲波回波特征參數向量θ′=[αGfc]作為氣體超聲換能器一致性評價的依據。3個特征參數都決定回波信號的特征。α作為帶寬因子,決定回波信號在時域中的持續時間。α越大,則持續時間越短;反之,則持續時間越長。同時,α也體現了回波信號幅值變化的速度。G作為回波信號增益值,反映了超聲波換能器的對射靈敏度。G越大,則對射靈敏度越小。

基于非線性模型的參數估計方法主要有高斯-牛頓算法和模擬退火算法。高斯-牛頓算法極大地依賴于初始值的設定,極易陷入局部最優解。模擬退火算法收斂速度慢、計算耗時長。人工魚群算法是在動物群體智能行為研究基礎上提出的1種新型優化方法,采用自下而上的設計方法。人工魚群算法具有較好的全局尋優能力,能避免陷入局部最優解;對初始參數設定的敏感性較低,允許范圍較大[10]。因此,本文將人工魚群算法應用于超聲換能器回波信號特征參數的最優估計。

人工魚群算法流程如圖4所示。

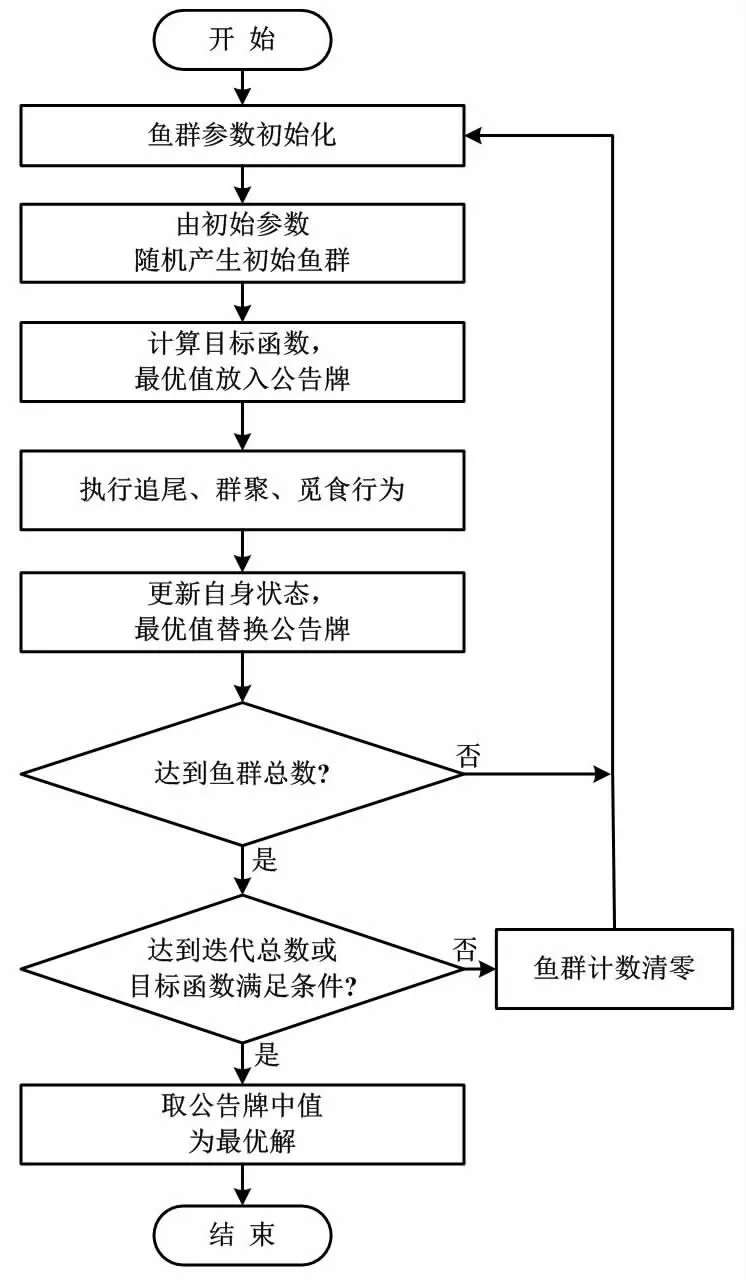
圖4 人工魚群算法流程圖

4 方法實施

4.1 硬件設計

超聲換能器動態性能測試系統硬件如圖5所示。

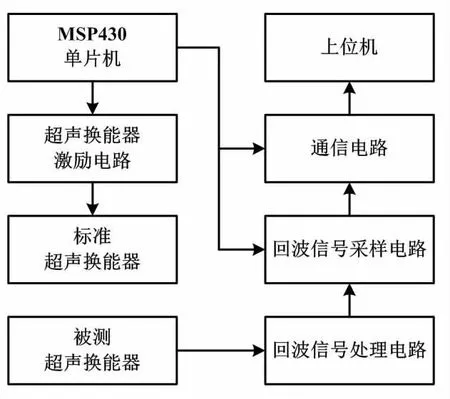
圖5 超聲換能器動態性能測試系統硬件框圖

超聲換能器動態性能測試系統采用MSP430單片機控制,主要包括激勵電路、回波信號處理電路、回波信號采樣電路和通信電路。由于超聲波信號在氣體中的衰減較大,需要較高的電壓激勵超聲換能器。直流升壓電路將電壓升至20 V,激勵的脈沖信號由TDC-GP22芯片產生。脈沖信號的頻率和個數可根據需要更改。脈沖信號通過控制場效應管以驅動變壓器。由于回波信號仍難以滿足測量要求,其接收后還需要先經過差分放大、濾波和二級放大處理,再經過高速采樣電路,最后將回波數據發送給上位機。

根據香農采樣定理,采樣頻率必須高于信號頻率2倍以上,并且采樣頻率越高則信號失真度越小。由于超聲波回波信號的頻率為200 kHz左右,采樣電路的采樣頻率為5 MHz。高速模擬/數字(analog-to-digital,A/D)采樣電路由復雜可編程邏輯器件(complex programmable logic device,CPLD)控制。當接收到單片機發出的采樣信號后,CPLD控制A/D采樣芯片采集回波信號,并將數據存儲于存儲芯片之中。采樣結束后,CPLD將數據傳送至單片機。單片機通過串行通信電路將數據傳輸至上位機。A/D采樣芯片選用AD9237芯片。該芯片的采樣頻率可達20 MHz。CPLD芯片選用EMP240T100C5芯片。晶振頻率選用50 MHz。

4.2 軟件設計

軟件設計包括單片機軟件與上位機軟件設計。

單片機程序主要包括回波信號處理、采集以及傳輸。單片機程序流程如圖6所示。

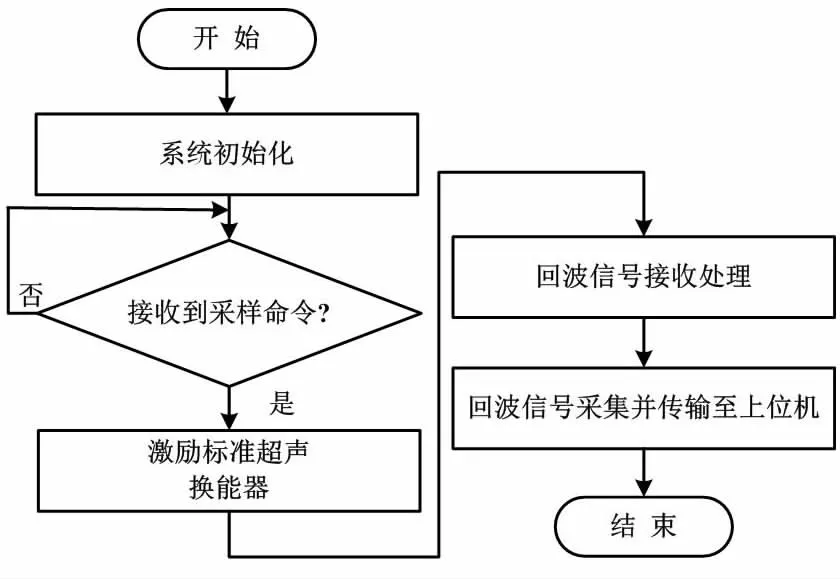
圖6 單片機程序流程圖

上位機采用Matlab軟件進行編程。程序主要由串口通信模塊、回波參數估計模塊和超聲換能器一致性匹配模塊3個部分構成。超聲換能器一致性匹配模塊根據各超聲換能器回波參數計算出歐式距離,并作為超聲換能器的一致性判斷標準,獲得回波參數一致性較好的換能器配對以及顯示其編號。

5 試驗驗證

超聲換能器回波信號特征參數如表1所示。

表1 超聲換能器回波信號特征參數

本文選用編號為1～13號的共13只超聲換能器進行動態性能測試。試驗在溫度為25 ℃、壓力為101 kPa的空氣環境下進行, 測量1～13號超聲換能器的回波信號,并由人工魚群算法得到回波信號特征參數。

由表1可知α、G、fc這3個特征參數的量級差距,因此在對換能器特征參數進行比較之前需要對參數進行歸一化處理。

本文將被測超聲換能器的帶寬因子α合并為數組[α1,α2,…,α13],則α的歸一化處理表達式為:

(7)

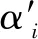
G和fc的歸一化處理方法與α一致。

試驗選取7號超聲換能器,通過式(3)計算7號超聲換能器與其他12個超聲換能器的歐式距離。7號超聲換能器與其他超聲換能器的歐式距離如表2所示。

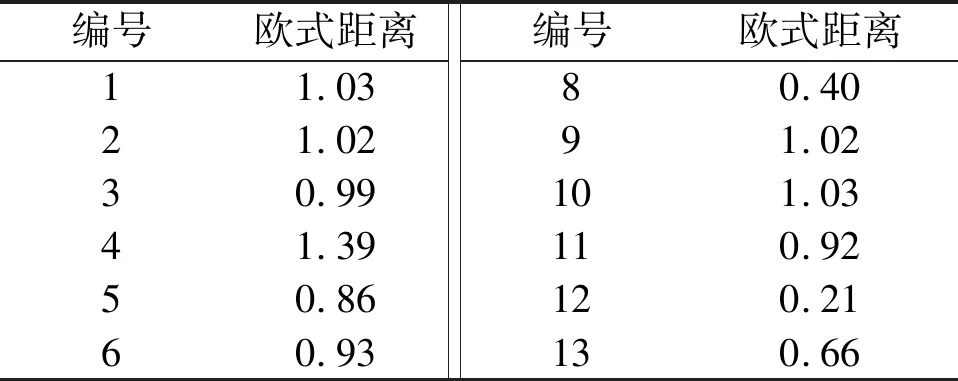
表2 7號超聲換能器與其他超聲換能器的歐式距離

由表2可知:7號超聲換能器與12號超聲換能器的一致性最好;7號超聲換能器與4號超聲換能器的一致性較差。因此,本文采用以上2組超聲換能器分別進行流量測量試驗。試驗管徑為DN50,安裝角度為45°。試驗流量測量裝置為LQB-1000臨界流文丘里音速噴嘴裝置。裝置的精度為0.3級,測量范圍為0.9～2 500 m3/h。

按照《超聲流量計檢定規程》(JJG 1030—2007)要求[11],本文對2組超聲換能器組成的流量計樣機進行各流量點的重復3次流量試驗。重復性的計算式為:

(8)

超聲換能器流量測量結果如表3所示。

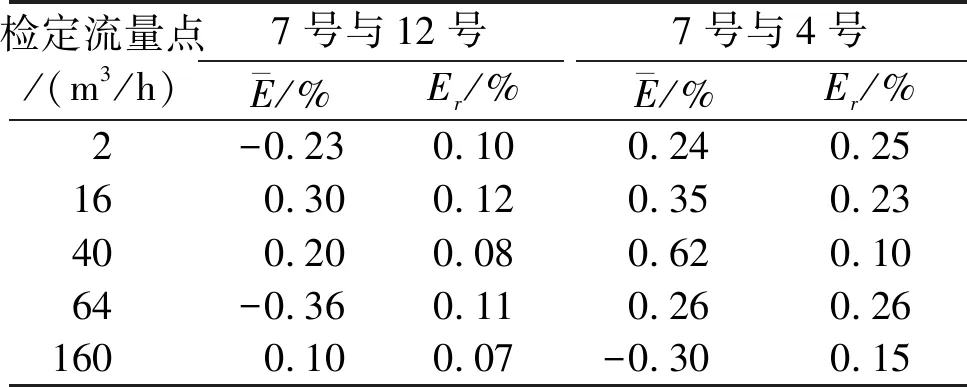
表3 超聲換能器流量測量結果

由表3可知,動態性能較好的7號和12號這對超聲換能器流量測量的誤差和重復性優于動態性能較差的7號超聲換能器和4號超聲換能器。尤其在小流量的測量中,7號超聲換能器和12號換能器的重復性更優。這是因為超聲換能器的動態性能越接近,靜態時差隨工況變化和零漂越小,小流量測量的誤差與重復性越好。

6 結論

本文提出了1種超聲換能器動態性能測試方法。該方法根據回波信號的特征,首先建立回波信號的高斯模型,通過人工魚群算法計算出高斯模型的最優特征參數;然后,將最優特征參數進行歸一化,計算超聲換能器間的歐式距離,以評價超聲換能器的動態性能一致性。本文設計了超聲換能器動態性能測試系統并進行相應試驗研究。試驗結果表明,動態性能一致性較優的超聲換能器,其流量測量誤差以及重復性均優于動態性能一致性較差的超聲換能器。