基于任務效能的傾轉旋翼機能力需求指標優(yōu)化方法

王高峰，張廣林，何振亞

1.中國航空工業(yè)發(fā)展研究中心，北京 100029

2.中國航空研究院，北京 100029

隨著交通強國、航空強國的提出與市場的不斷發(fā)展,時間成本在航空任務中的比重不斷提高,民用直升機即將面對一輪新的升級換代需求[1]。傾轉旋翼機具有航程遠、速度快、垂直起降的性能特點,以傾轉旋翼機為代表的高速旋翼飛行器能夠有效支撐我國交通運輸體系、應急救援體系建設,填補相關領域能力空白。但新型民用高速旋翼飛行器缺乏參考樣機和統(tǒng)計數(shù)據(jù),在前期設計階段難以準確地根據(jù)市場需要提取各項能力指標需求,對各項指標進行權衡優(yōu)化,難以有效對后續(xù)論證、研制過程提供指導參考。本文采用優(yōu)化設計方法對傾轉旋翼機的能力需求指標進行優(yōu)化研究,具有重要的工程應用價值。

進入21 世紀以來,國外就逐步將最優(yōu)化、多目標優(yōu)化技術引入直升機設計中,針對直升機、旋翼機的總體設計、分系統(tǒng)設計等開展了優(yōu)化研究[2-3]。近年來,國內各航空航天高校及院所通過傳統(tǒng)迭代法、神經(jīng)網(wǎng)絡、蟻群算法、遺傳算法等方法針對固定翼、旋翼飛行器的總體參數(shù)[4-7]、部分系統(tǒng)[8-11]開展了優(yōu)化研究。但上述研究沒有與需求指標和效能評估形成有機結合,沒有解決“如何從市場中得到傾轉旋翼機的能力需求指標,基于其生成優(yōu)化后的能力需求指標序列以指導論證、研制過程”這個問題。

本文以國內外相關研究為基礎,基于K-Means聚類分析方法、粒子群算法（PSO）、傾轉旋翼機性能估算模型,構建了一種基于任務需求分析及效能仿真的傾轉旋翼機能力需求指標優(yōu)化方法,能夠以任務（集）為輸入,整理分析并得到一系列任務簇,在每個任務簇中開展基于任務效能仿真的能力需求指標優(yōu)化計算,最終輸出優(yōu)化后的效能最優(yōu)且可行的傾轉旋翼機性能指標、技術指標序列,為論證、研制等過程提供支撐和參考。

1 優(yōu)化方法總流程結構

本文旨在構建一套從任務剖面（集）開始,基于任務效能的性能指標優(yōu)化方法。圖1 為優(yōu)化方法的總體流程架構,主要包括任務剖面分析、效能仿真、傾轉旋翼機模型、粒子群優(yōu)化4個主要模塊。

本文的主要輸入為需求端收集的典型任務剖面/任務想定數(shù)據(jù)集,主要輸出為針對各任務簇的傾轉旋翼機最優(yōu)設計點位的技術參數(shù)、性能參數(shù)序列,優(yōu)化方法流程如圖1所示。

分析—優(yōu)化的流程如下:（1）對任務剖面進行分析,根據(jù)給定和調研得到的任務剖面/任務想定集,以及關注的主要任務領域,調整效能計算方法,構建任務仿真模型；（2）對任務剖面集進行聚類分析,計算最優(yōu)聚類數(shù),將其分為可由型號A、B、C等覆蓋的任務簇,并計算得到各任務簇的性能需求范圍；（3）綜合性能需求范圍、技術發(fā)展約束、傾轉旋翼機模型,構建由可行設計點位構成的可行設計空間；（4）在可行設計空間中通過粒子群優(yōu)化算法尋找任務效能最優(yōu)的設計點位,并輸出其技術參數(shù)和性能參數(shù)。

本文構建的優(yōu)化方法流程適用于直升機、傾轉旋翼機等航空裝備,通過調整性能計算模型、效能仿真模型即可實現(xiàn)遷移應用。

2 K-Means聚類分析方法

K-Means聚類分析方法于1956年由Steinhaus提出,具有無監(jiān)督、解釋性好的優(yōu)點,對大量模糊數(shù)據(jù)的聚類分析具有良好的適用性。聚類分析算法的核心思想是對于給定數(shù)據(jù)集D及聚類數(shù)k,通過迭代分類計算的方法構建給定數(shù)量的聚類簇,且使各簇內對象距所屬聚類中心的歐氏距離之和最小,即

式中,xi為數(shù)據(jù)集中的對象成員,μk為各簇的聚類中心點。

傳統(tǒng)的K-Means 聚類算法初始聚類中心是隨機生成的,在聚類空間中的分布并不均勻,可能導致聚類效果不穩(wěn)定。可以參照相關改進算法,通過對初始聚類中心的預處理對算法進行優(yōu)化,消除初始聚類中心的隨機性,使其在聚類空間中形成相對均勻的分布[12]。改進算法步驟如圖2所示。其中,聚類輸入包括數(shù)據(jù)集D,以及聚類簇數(shù)k；聚類輸出為k個聚類簇的聚類結果。

圖1 優(yōu)化方法流程Fig.1 Flowchart of optimization method

圖2 K-Means聚類算法流程Fig.2 Flowchart of K-Means clustering algorithm

具體步驟為:（1）對數(shù)據(jù)集D中的任意兩個樣本的歐氏距離進行計算:dist(xi,xj)= ||xi-xj||2；（2）選擇所有聚類樣本組合中總歐氏距離最小的一點xi作為初始聚類中心μ1；（3）對數(shù)據(jù)集D中任意對象成員xi進行遍歷,計算其與目前最近的聚類中心μk的歐氏距離dist(xi,μk)；（4）對dist(xi,μk)進行排序并計算平均距離Jave,遍歷得首個使dist(xi,μk)≥Jave的對象成員xi,作為下一個聚類中心μk；（5）重復步驟（3）和（4）,直到完成所有聚類中心的初始化；（6）對聚類簇進行計算。

相比于原方法,該方法能夠進一步提高初始聚類中心點分布的均勻性,提高聚類效果的穩(wěn)定性。

3 粒子群算法

粒子群算法是一種進化計算算法,由Kennedy 和Eberhart 基于最優(yōu)化原則提出。其基本思想是通過群體中個體之間的協(xié)作和信息共享來尋找全局最優(yōu)解。粒子群算法實現(xiàn)相對簡單容易,沒有許多參數(shù)的調節(jié),適用于連續(xù)問題的全局尋優(yōu)[13]。

粒子群算法核心原理是:粒子群分散在搜索空間中對代價函數(shù)局部最優(yōu)解進行求解,并通過在粒子群中共享局部最優(yōu)解以確定當前時刻的全局最優(yōu)解,根據(jù)當前時刻和歷史狀態(tài)的解集信息對粒子的速度和位置等進行調整更新。因此粒子群優(yōu)化共包含局部、全局兩個維度,其基本數(shù)學描述為

式中,i=1, 2, 3, …,n,n為粒子群的粒子總數(shù)；ω為慣性因子；vi為粒子的速度；xi為粒子的當前位置；c1,c2為局部、全局學習因子；rand()為隨機修正系數(shù)；lbesti, gbesti分別為當前時刻局部最優(yōu)解、全局最優(yōu)解的位置。

因此,式（2）可以分為三部分:（1）ω?vi為記憶項（慣性項）,表示上次速度大小和方向對搜索方向的影響,一般來說,慣性越強,全局尋優(yōu)能力越強,局部尋優(yōu)能力越弱,更難陷入局部最優(yōu)解；（2）c1?rand()?(lbesti-xi)為局部項,表示全局搜索方向的一部分來自粒子自身的經(jīng)驗,即粒子局部最優(yōu)對搜索方向的影響；（3）c2?rand()?(gbesti-xi)為全局項,表示全局搜索方向的一部分來自粒子群的共享信息,即粒子群全局最優(yōu)解對搜索方向的影響。

rand()表示這種影響是相對隨機的,粒子通過自身的經(jīng)驗和全局的經(jīng)驗決定下一步的運動（速度）,進而確定下一個位置。以式（1）和式（2）為基礎,形成了粒子群算法的一般形式。

對于給定最大迭代次數(shù)Gk的優(yōu)化過程,可以通過線性遞減權值（LDW）策略對慣性因子、學習因子進行調整,增強粒子群的全局尋優(yōu)能力。

式中,g為當前的迭代次數(shù)。一般可以取c1+c2=C保證速度的穩(wěn)定性,其中C為選定常數(shù),與尋優(yōu)速度及精度有關。

粒子群算法的計算流程如圖3所示。

4 傾轉旋翼機性能估算模型

對于基于任務效能的傾轉旋翼機能力需求指標優(yōu)化問題來說,一方面需要構建優(yōu)化問題的約束與邊界；另一方面需要構建能夠支撐任務仿真的性能估算模型。對傾轉旋翼機的總體性能參數(shù)估算模型進行簡化,使用該模型隱式地描述各項性能參數(shù)之間的約束關系,并通過調整技術參數(shù)輸入來影響性能參數(shù)。因為技術參數(shù)之間的耦合關系較弱,其范圍約束容易通過技術發(fā)展曲線進行描述和預測,因此可以通過該方法構建基于該模型的可行設計空間,為優(yōu)化問題提供約束,同時將其作為性能仿真模塊嵌入仿真模擬流程,支撐仿真評估。

圖3 粒子群算法流程Fig.3 Flowchart of particle swarm optimization algorithm

針對仿真優(yōu)化計算需求,梳理了主要技術參數(shù)、性能參數(shù),詳見表1,本文采用逆向設計的思路,并構建簡化后的基于各項技術參數(shù)的性能估算方法[14-15],對于不同的精度或研究需求,可以對估算模型進行修正或調整,以適應不同問題的研究需要,傾轉旋翼機性能估算流程如圖4所示。

表1 主要技術參數(shù)、性能參數(shù)表Table 1 Table of main technical parameters and performance parameters

4.1 直升機模式性能估算

傾轉旋翼機的最大起飛重量為

對傾轉旋翼機的旋翼半徑進行計算

圖4 傾轉旋翼機性能估算流程圖Fig.4 Flowchart of tiltrotor aircraft performance estimation

式中,kb為旋翼數(shù)量。

當?shù)乩σ蜃觙F、功率因子fN為

式中,ρ為當?shù)乜諝饷芏取ａ槍γ總€旋翼進行分析,取考慮垂直增重系數(shù)fcz后的當前發(fā)動機輸出總拉力為T,地效增長系數(shù)為fge,則拉力系數(shù)為

對誘導速度vi進行計算,進而計算各旋翼的總誘導功率Pin

式中,J0為誘導功率修正系數(shù)。取當?shù)匕l(fā)動機輸出功率為pH,型阻功率為pxP,則此時即可計算得到當前當?shù)氐氖Ｓ喙β?/p>

此時即可計算垂直爬升率vvc及懸停耗油率sfch,當vvc≤0.5m/s時,認為此時到達懸停升限hh,考慮地效增長系數(shù)fge即可計算得到最大起降高度hto。

定義前進比μ為前飛速度vf與槳尖速度ωR之比

取前飛狀態(tài)下旋翼拉力為T,拉力系數(shù)CT滿足如下關系

進一步對量綱一誘導速度vi進行求解,可以對量綱一誘導功率Pin進行計算。

與懸停模式同理,可根據(jù)當?shù)匕l(fā)動機輸出功率對剩余功率pre進行計算,進而求解直升機模式斜爬升率vlc。

4.2 固定翼模式性能估算

對機翼面積進行估算

式中,R為旋翼半徑,kLR為旋翼直徑與機翼展長的比值。此時升力、阻力系數(shù)為

式中,vf為前飛速度；CD0為零升阻力；δ為誘導阻力修正因子；CDi為升致阻力。

假定固定翼模式下發(fā)動機輸出功率主要用于克服前飛氣動阻力,忽略其他阻力項,取功率轉化到旋翼/螺旋槳的效率為kpD,則此時克服阻力的輸出功率為

傾轉旋翼機的剩余功率為

此時即可計算斜爬升率vfc、前飛耗油率sfcf、實用升限hc。

輸出功率曲線與當?shù)毓β实慕稽c即為當?shù)刈畲笏俣葀max,對輸出功率曲線進行分析,即可得到久航速度、遠航速度,進而計算得到航程R、航時E、巡航速度vc等參數(shù)。

5 傾轉旋翼機能力需求指標優(yōu)化

5.1 市場需求聚類分析

本文選用了一個共有187個樣本的直升機/旋翼機任務需求調研數(shù)據(jù)集對真實的市場需求進行模擬,數(shù)據(jù)集包括載荷需求、速度需求、航程需求、起降高度需求、升限需求5個維度。

5.1.1 型號序列需求分析

傾轉旋翼機的市場需求差異較大,無法通過某種特定的型號完成對市場的完全覆蓋,因此需要對市場需求進行分類,將其整理為若干相對獨立的需求簇,分別選用不同的型號進行差異化發(fā)展,覆蓋傾轉旋翼機市場的相關需求。

采用Gap Statistic 判據(jù)對最優(yōu)聚類數(shù)kc進行計算[16]；當某聚類數(shù)k對應的間隔統(tǒng)計量Gapk首次大于Gapk+1及采樣標準差sk+1之和時,認為此時存在kc=k。

對聚類緊支測度進行蒙特卡羅（Monte Carlo）采樣計算,每個聚類數(shù)k執(zhí)行1000次采樣。任務集總歐氏距離平方和（SSE）及間隔統(tǒng)計量Gap隨聚類數(shù)k的變化曲線如圖5所示。

根據(jù)Gap Statistic 判據(jù),可以看出當k=4 時,Gap 到達局部峰值,此時Gap4首次大于Gap5及采樣標準差s5之和,因此對應選定任務集的最佳聚類數(shù)kc=4,即在當前的市場情況下,共需要4型不同的傾轉旋翼機以滿足市場需求。

5.1.2 能力需求指標分析

針對最優(yōu)分類情況進行聚類分析,可以計算得到共4個不同任務簇下各特征分位點（對應的需求覆蓋率:75%覆蓋率、μ+3σ分位點、100%完全覆蓋）下各任務簇能力需求表,見表2。

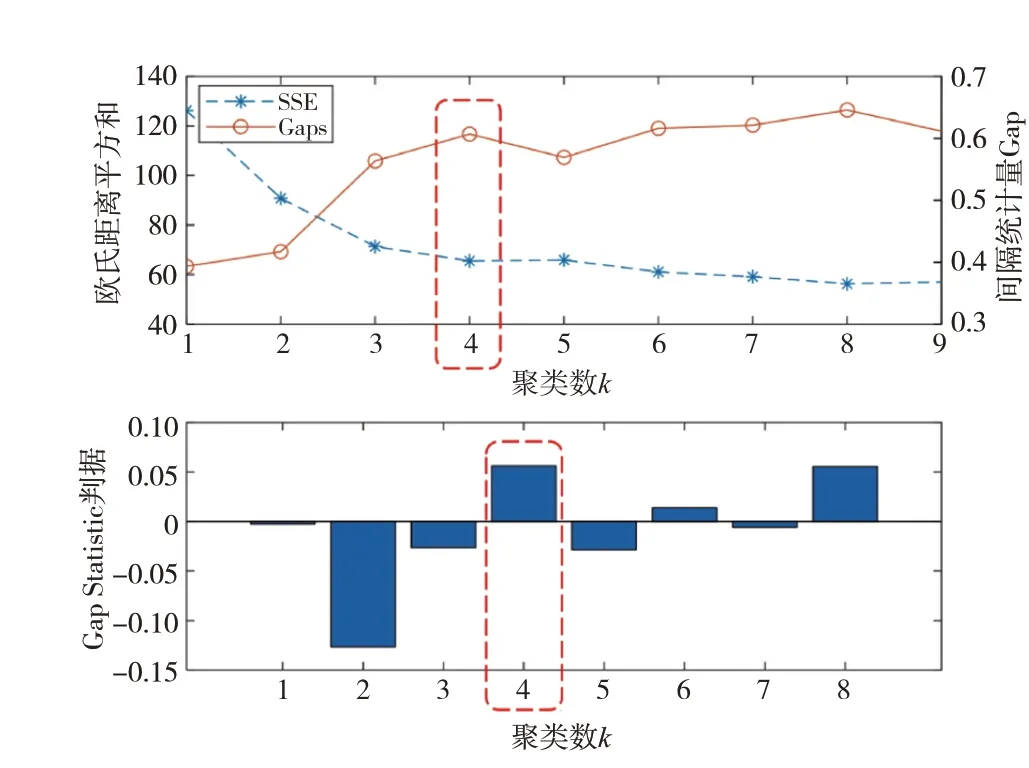
圖5 SSE/Gap隨聚類數(shù)k變化曲線Fig.5 The curve of SSE/Gap changes with the number of clusters k

表2 各任務簇不同分位點下的能力需求表Table 2 Table of capability requirements at different quantile for each task cluster

對性能需求歸一化后的相對性能需求如圖6所示。可以看出,對于給定的任務簇,可能存在某任務與其他任務差距較大的情況,即異常需求,此時該任務的需求指標相對其他任務明顯較大,覆蓋該任務所需要的代價顯著大于其他任務。通過μ+3σ分位點對異常需求項進行過濾,可以得到各任務簇下對應的最優(yōu)覆蓋率,見表3。

5.2 任務仿真計算

選取任務簇2作為未來民用傾轉旋翼機的首要發(fā)展方向。通過μ+3σ分位點對異常需求項進行過濾,根據(jù)得到的能力需求指標構建典型航空交通運輸任務剖面,如圖7 所示,并對能力需求指標優(yōu)化提供仿真場景及約束。

圖6 各任務簇歸一化性能需求對比Fig.6 Chart of normalized performance requirements comparison for each task cluster

表3 各任務簇最優(yōu)覆蓋率對比Table 3 Table of optimal coverage rate for each task cluster

傾轉旋翼機在選定任務想定下的任務流程為:（1）傾轉旋翼機搭載5041kg 艙內載荷,從A 點垂直起飛,起飛機場當?shù)睾０胃叨?750m；（2）短暫爬升至安全高度后,傾轉旋翼機以固定翼模式爬升至5800m 高度至B 點,爬升距離為10km；（3）傾轉旋翼機在5800km 海拔高度,以巡航模式飛行1230km至C點；（4）以固定翼模式從C點下降至D點,完成著陸,總航程1260km。

對該任務剖面想定進行仿真計算,以運載量W、總任務耗時ttot、總任務耗油cf為主要任務表現(xiàn)指標,構建任務效能評估方法

則效能指標E能夠表現(xiàn)該（選定能力需求指標下）傾轉旋翼機單位油耗對其單位時間運力的貢獻。

以此為優(yōu)化目標,優(yōu)化得到的能力需求指標序列即為在滿足該任務簇能力需求下“油耗—單位時間運力”轉化比最高的傾轉旋翼機能力需求指標序列,可以用于支撐方案論證或指導概念方案設計。

5.3 能力需求指標優(yōu)化

基于粒子群算法,開展雙傾轉旋翼機能力需求指標優(yōu)化研究,迭代優(yōu)化曲線如圖8所示,優(yōu)化結果見表4、表5,其中各項性能指標為海平面高度下性能表現(xiàn)指標。優(yōu)化后的傾轉旋翼機在任務中的表現(xiàn)參數(shù)見表5。

綜上可以看出,在滿足任務簇2能力需求的情況下,能力需求指標優(yōu)化算法可以有效地將任務需求參數(shù)轉化為能夠用于指導型號論證及概念方案設計的技術指標、性能指標參數(shù),且保證有較好的效能水平。

圖7 基于性能需求約束的交通運輸任務剖面Fig.7 Transportation mission profile based on performance requirements constraints

圖8 任務效能—優(yōu)化代數(shù)變化曲線Fig.8 Curve of task efficiency-optimization generation variations

5.4 優(yōu)化模型的擴展應用

本研究構建的優(yōu)化方法流程除適用于傾轉旋翼機外,還具有較強的可拓展性,可以通過調整傾轉旋翼機/直升機模型、效能仿真模型（見圖1）,對其他構型飛行器進行分析優(yōu)化。

以常規(guī)構型直升機為例,構建直升機懸停、前飛等模式下的性能估算模型[14],以前述傾轉旋翼機噸位、載荷能力為參考,以任務效能最大化為優(yōu)化目標,進行迭代優(yōu)化,直升機任務剖面如圖9所示。直升機在選定任務想定下的任務流程為:（1）直升機搭載5041kg 艙內載荷,從A 點垂直起飛,起飛機場當?shù)睾０胃叨?750m；（2）短暫爬升至安全高度后,直升機在3500m 高度從B 點巡航飛行至C 點；（3）直升機從C點下降至D點,完成著陸,總航程650km。優(yōu)化迭代曲線如圖10所示,優(yōu)化結果見表6、表7。

綜上可以看出,通過將傾轉旋翼機模型、效能仿真模型替換為直升機模型、直升機任務效能仿真計算模型,可以對常規(guī)構型直升機的各項技術參數(shù)、性能參數(shù)進行迭代優(yōu)化,優(yōu)化方法具有良好的可擴展性。其中模型精度越高,優(yōu)化效果越好。

表4 優(yōu)化輸出技術參數(shù)、性能參數(shù)Table 4 Table of technical parameters and performance parameters optimized

表5 優(yōu)化結果任務仿真輸出統(tǒng)計Table 5 Table of simulation outputs for optimized results of tasks

6 結論

本文選用了一個共有187個樣本的直升機/旋翼機任務需求調研數(shù)據(jù)集對真實的市場需求進行模擬,以雙傾轉旋翼機為例,針對能力需求指標參數(shù)進行了優(yōu)化計算。

圖9 直升機交通運輸任務剖面Fig.9 Transportation mission profile for helicopter

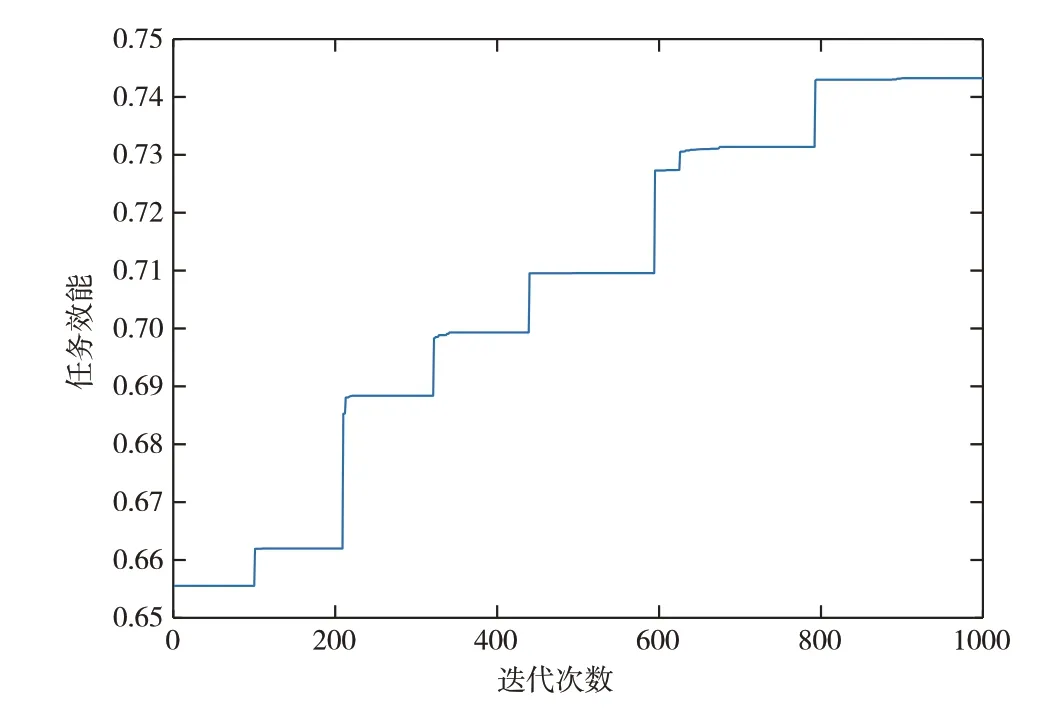
圖10 直升機任務效能—優(yōu)化代數(shù)變化曲線Fig.10 Curve of task efficiency-optimization generation variations for helicopter

（1）基于K-Means 聚類分析方法及Gap Statistic 判據(jù),未來以傾轉旋翼機為代表的民用高速旋翼機市場需求主要可以由4種不同型號覆蓋,應用場景主要集中在平原、次高原地區(qū),載荷需求從500kg到22.3t不等。

（2）傾轉旋翼機能力需求指標優(yōu)化方法能夠綜合考慮各性能參數(shù)、任務表現(xiàn)參數(shù)之間的耦合關系,能夠考慮不同指標項之間的矛盾需求,輸出能夠用于指導型號論證及概念方案設計的技術指標、性能指標參數(shù)。

（3）本文提出的基于效能仿真和粒子群算法的優(yōu)化方法流程可以有效適用于傾轉旋翼機、常規(guī)構型直升機等航空裝備,優(yōu)化結果相對合理,具有良好的可擴展性。

表6 直升機優(yōu)化輸出技術參數(shù)、性能參數(shù)表Table 6 Table of technical parameters and performance parameters optimized for helicopter

表7 直升機優(yōu)化結果任務仿真輸出統(tǒng)計Table 7 Table of simulation outputs for optimized results of tasks for helicopter