一種艦船搖擺下基于正弦空間的多波束覆蓋范圍計算方法
趙海東,付 林,賈 然
(中國船舶集團有限公司第八研究院,南京 211153)
0 引 言
艦船航行時發生的縱搖、橫搖和航向的改變對雷達的波束指向及空間覆蓋影響很大。為了保障雷達系統的指向精度,無機械穩定平臺的波束穩定系統一般都采用坐標變換技術[1-2],在雷達天線方位和俯仰軸上對艦船搖擺姿態角進行角度實時補償,從而實現雷達天線波束指向的電子穩定。
在艦船搖擺運動過程中,陣面坐標系同一俯仰角的多個波束的覆蓋范圍會隨之不斷變化,大地坐標系的水平面往往被陣面坐標系的多個俯仰層的不同指向波束覆蓋,單個俯仰層的多波束已無法滿足對水平面的全覆蓋,須計算不同俯仰層在水平面的方位覆蓋范圍,通過俯仰層組合實現對水平面的組合覆蓋。
本文提出一種基于正弦空間[3]的多波束覆蓋范圍計算方法,利用正弦空間中波束形狀不變的特性,計算覆蓋水平面的俯仰層以及每個俯仰層下多波束的方位覆蓋范圍。
1 正弦空間
在大地坐標系下,在波束掃描時相控陣雷達天線的波寬隨著其偏離法線方向而展寬,同時波束形狀也有所變化,導致波束排列等問題復雜化。正弦空間是單元球面在陣列平面上的投影,如圖1[4]所示,陣列平面位于XOY。在正弦空間中,波束的形狀不隨掃描角變化,有利于對波束覆蓋進行分析和編排。在此坐標系下,波束寬度和角位置增量不用度、弧度,而是用其正弦或正弦增量來表示。θ和φ為球坐標系下的波束,α和β為波束在正弦空間中的坐標。
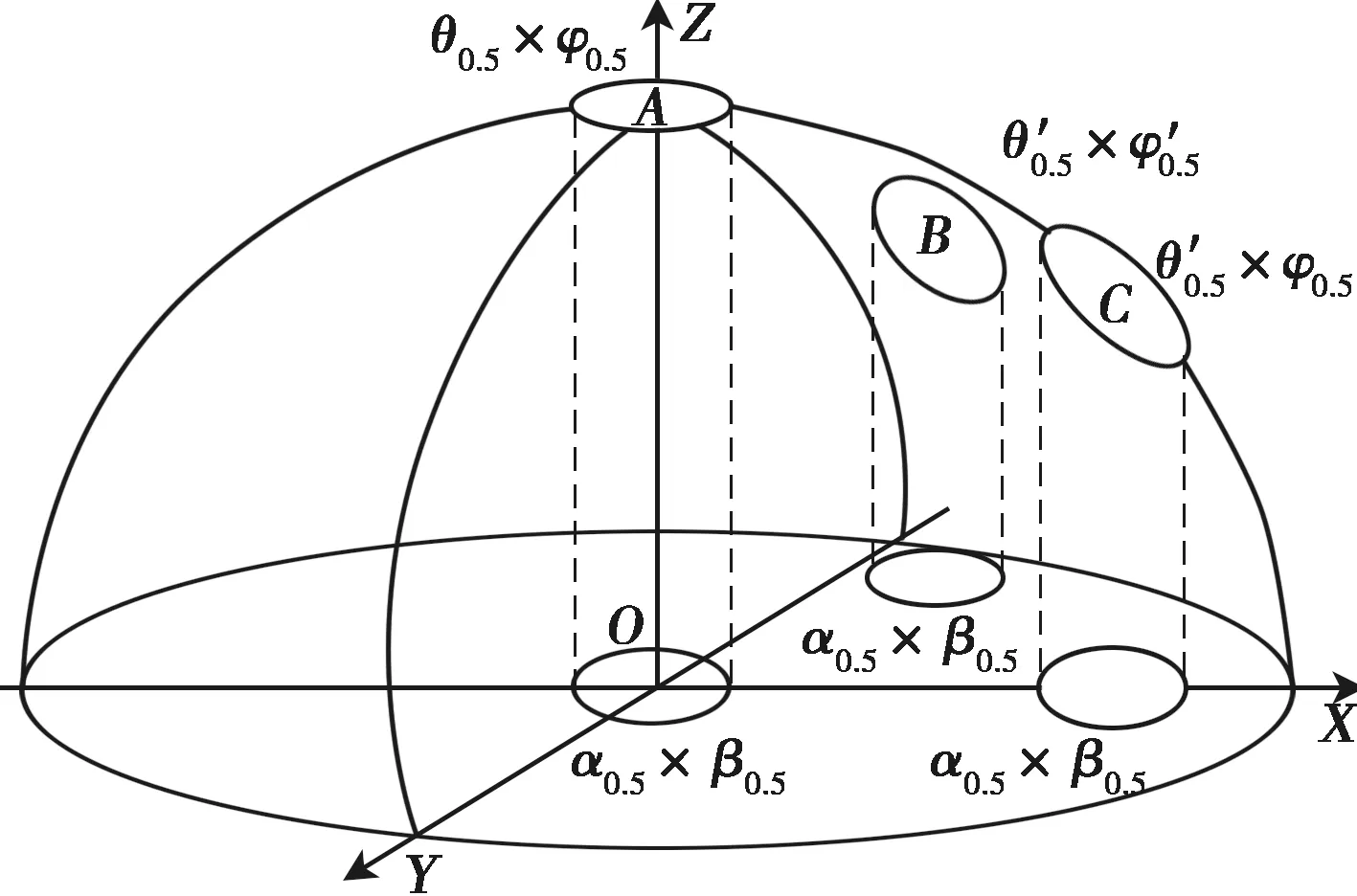
圖1 二維平面陣波束投影圖
2 坐標系轉換
在正弦空間下完成波束編排后,通常用陣面坐標系表示波位信息,而波束的實際覆蓋范圍則須要轉換至大地坐標系,涉及到正弦、陣面、大地3個坐標系間的轉換[5]。
(1)大地坐標系與陣面坐標系的轉換
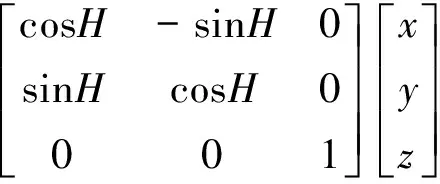
(1)
式中,H為航向角;P為縱搖角;Rl為橫搖角;Q為面陣安裝角;C為面陣傾斜角;(x,y,z)為波束在大地直角坐標系下的坐標,對應的大地球坐標系(圖2)可表示為
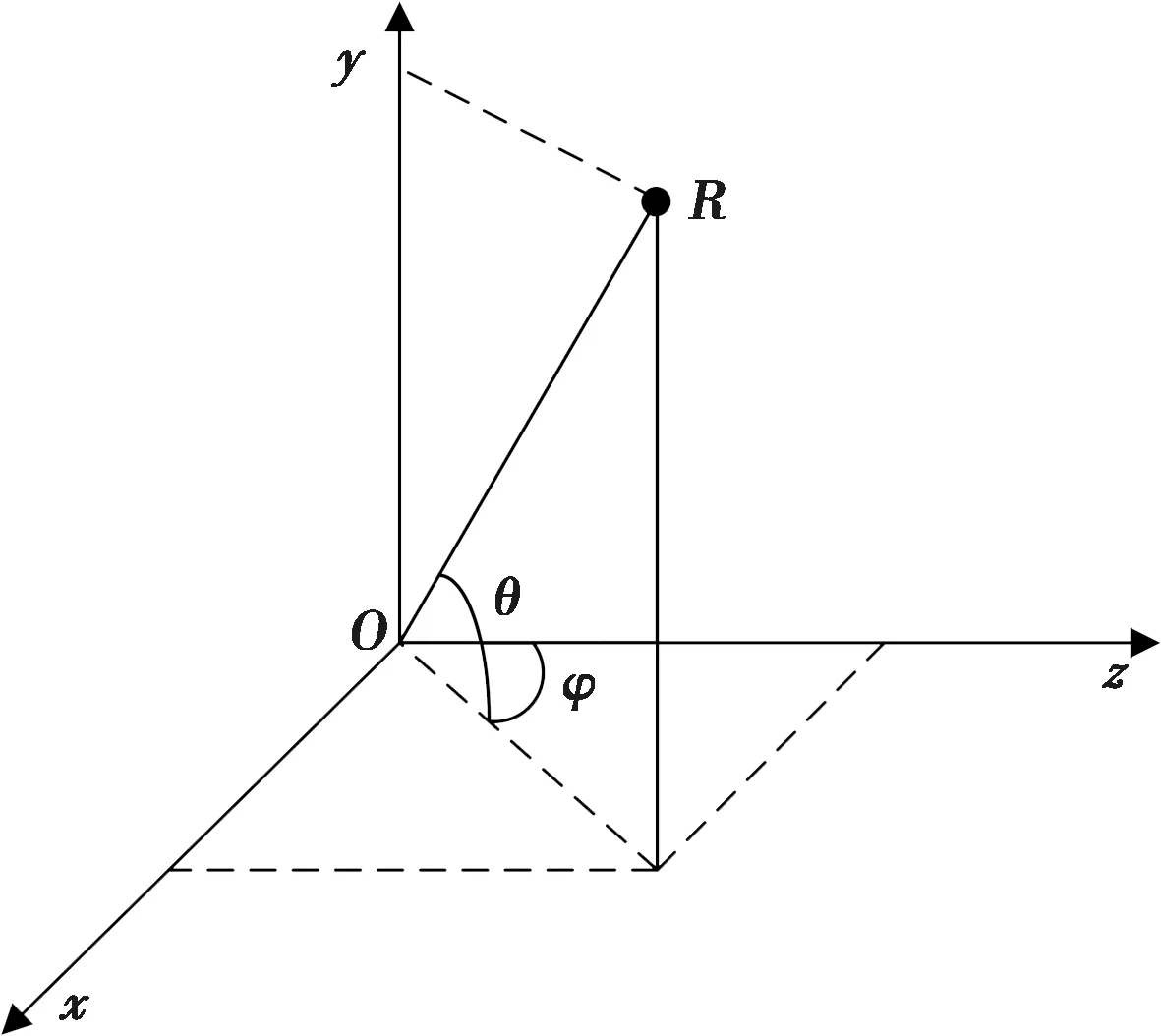
圖2 大地球坐標系
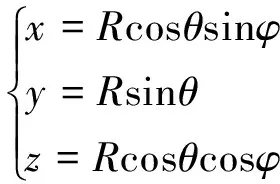
(2)
(xa,ya,za)為波束在陣面直角坐標系下的坐標,其對應的陣面球坐標系(圖3)可以表示為
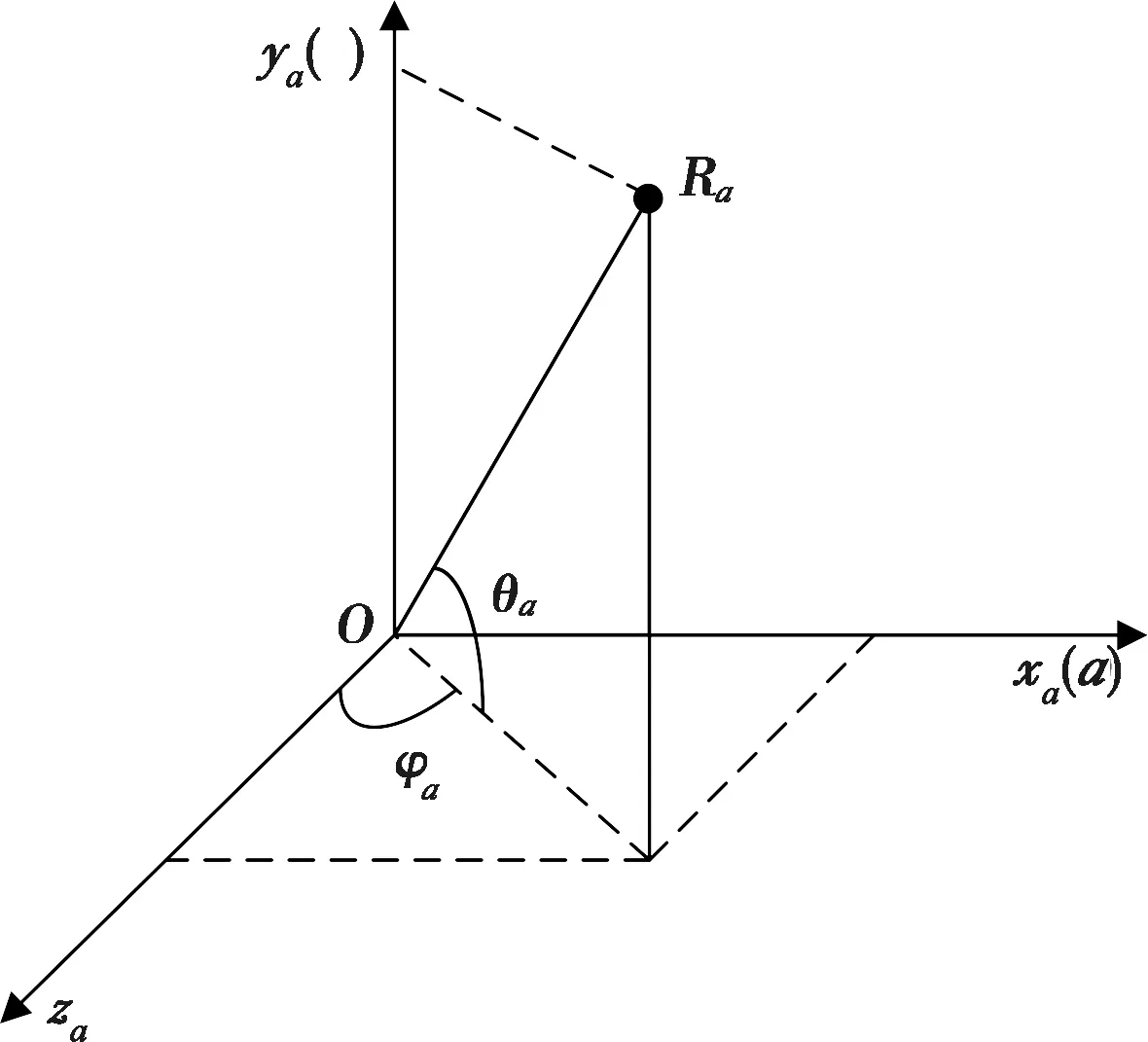
圖3 陣面球坐標系

(3)
(2)陣面坐標系與正弦坐標系的轉換
如圖3所示,陣面位于xaoya平面,xa即為正弦空間的α軸,ya為正弦空間的β軸,由此可得轉換關系:
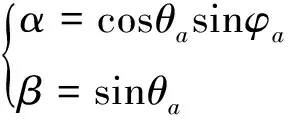
(4)
利用式(1)~(4)即可完成大地坐標系與正弦坐標系之間的轉換。
3 覆蓋范圍計算
在正弦空間中,可以通過計算某一坐標點與各波束之間的中心距離來確定此坐標點的覆蓋波束,本文通過此方法將水平面映射至正弦空間中,并按等間隔取點計算來選取覆蓋波束。具體步驟如下:
(1)確定面陣法線指向的大地方位AZ_Center,將大地坐標(AZ_Center,0)轉換至正弦空間中,得到初始點坐標(α0,β0),通過計算距離得到距離最近的波束,即此波束覆蓋(α0,β0),將該波束的俯仰層作為初始俯仰層k0;
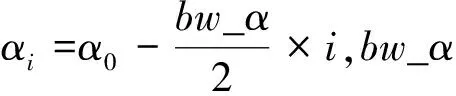
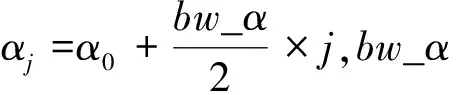
(4)合并第(2)、(3)步的計算結果,得到初始俯仰層k0在大地水平面的覆蓋范圍為[A0,B0];
(5)以第(2)步的終止坐標點為起始點,記此點俯仰層kn,n=1,2,3,…。同第(2)步一樣,依次選點往左計算,直至俯仰層變化時,將上一個坐標點和當前坐標點的中心值作為計算點,該點的大地方位即為俯仰層kn在大地水平面覆蓋范圍的左邊界An。俯仰層kn在大地水平面覆蓋范圍的右邊界Bn為上一俯仰層的左邊界。俯仰層kn在大地水平面的覆蓋范圍為[An,Bn]。當坐標點超過面陣覆蓋范圍左邊界時,停止往左計算;
(6)以第(3)步的終止坐標點為起始點,記此點俯仰層km,m=n,n+1,n+2,…。同第(3)步一樣,依次選點往右計算,直至俯仰層變化時,將上一個坐標點和當前坐標點的中心值作為計算點,該點的大地方位即為俯仰層km在大地水平面覆蓋范圍的右邊界Bm。俯仰層km在大地水平面覆蓋范圍的左邊界Am為上一俯仰層的右邊界。俯仰層km在大地水平面的覆蓋范圍為[Am,Bm]。當坐標點超過面陣覆蓋范圍右邊界時,停止往右計算。
4 仿真驗證
根據以上算法,設置仿真參數如表1所示。
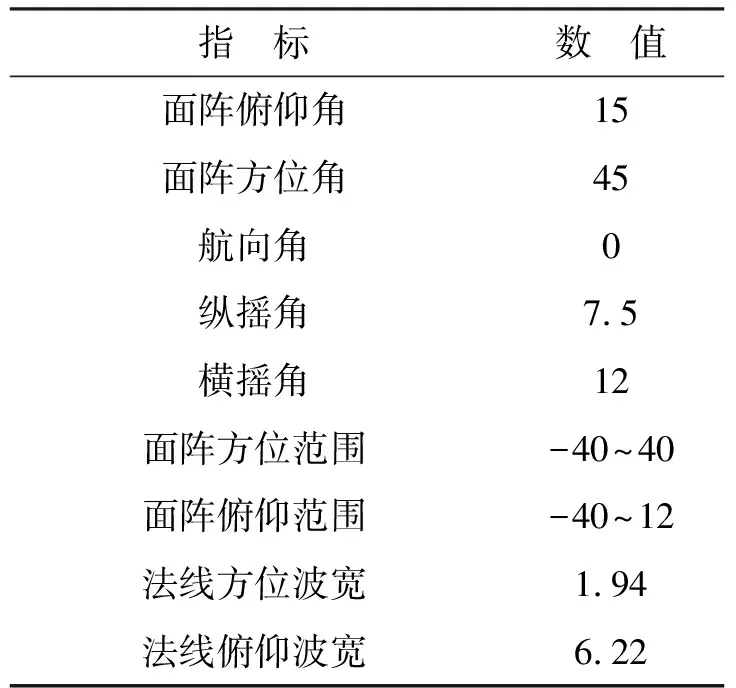
表1 仿真參數(單位:°)
將大地水平面映射至正弦空間中,結果如圖4所示,圖中‘+’表示在正弦空間中按照等間隔計算所選取的點。通過距離計算判斷俯仰層的覆蓋情況,結果如表2所示。
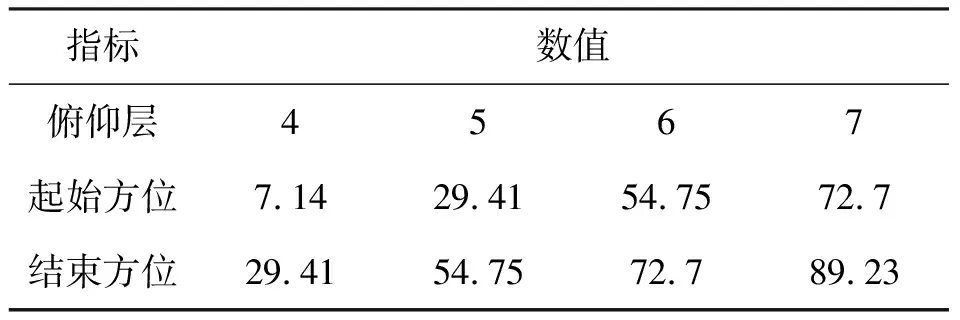
表2 計算結果(單位:°)
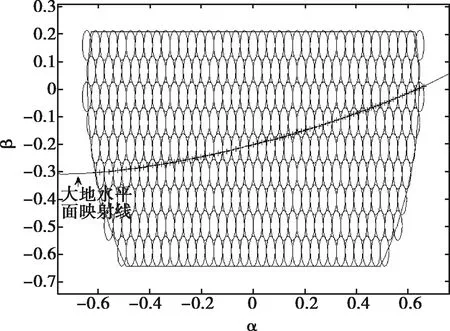
圖4 正弦空間下的波束分布
將上述結果的方位在大地坐標下畫出,結果如圖5所示,俯仰層從下往上記為俯仰層1,俯仰層2,…,俯仰層9。利用該方法計算出的覆蓋范圍與各俯仰層的實際水平面覆蓋范圍相吻合,驗證了該方法的有效性。
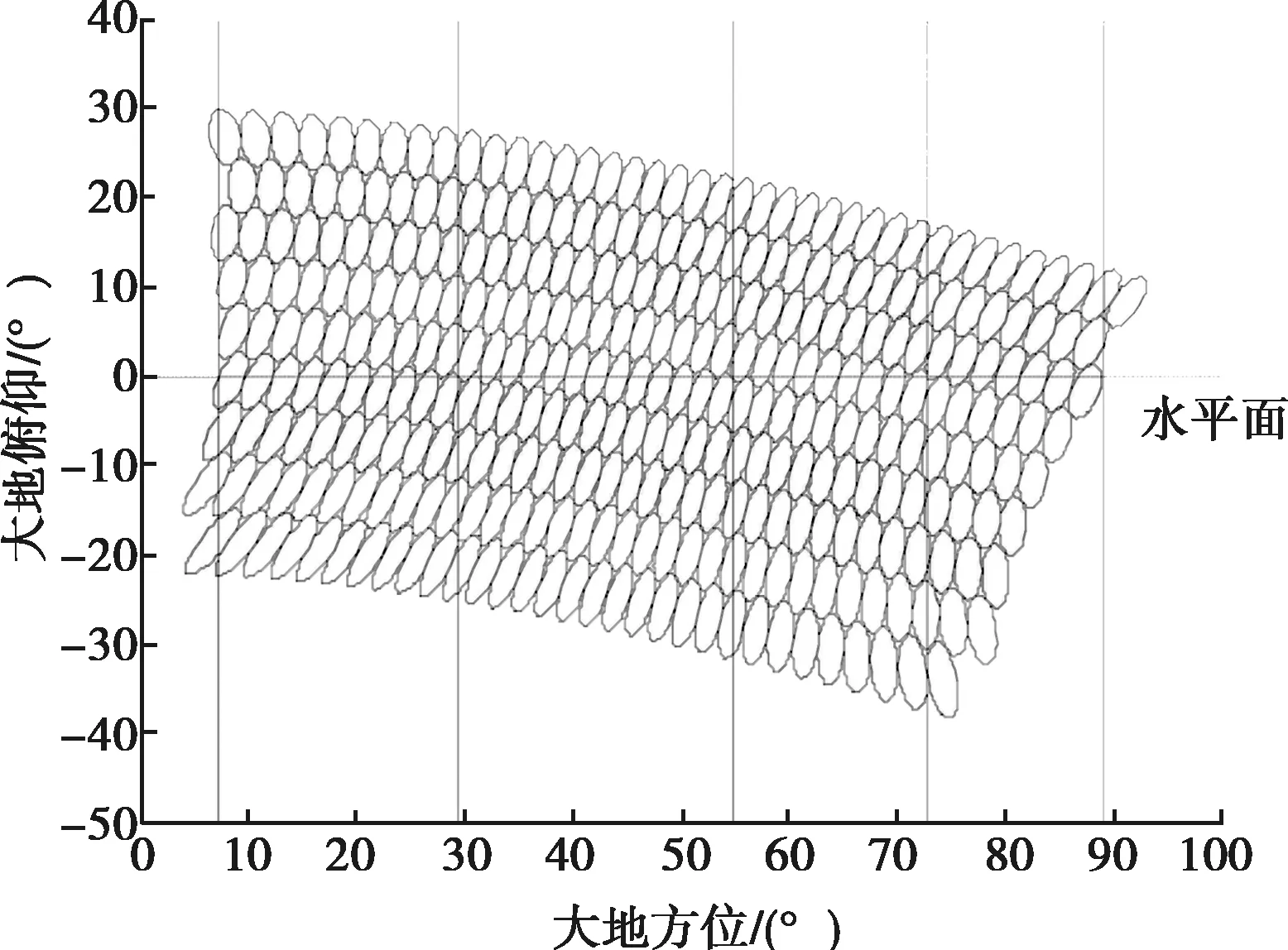
圖5 大地坐標下的波束覆蓋情況
5 結束語
本文針對艦船搖擺時多波束覆蓋范圍的不斷變化,提出了一種利用正弦空間中波束形狀不變的特性來計算多波束大地方位覆蓋范圍的方法,該方法將大地水平面映射至正弦空間中,通過在水平面映射線上按等間隔取點計算各俯仰層的覆蓋范圍,最后通過仿真實驗驗證了該方法的有效性,可為艦船搖擺下的波束調度提供理論依據。

