多尺度神經網絡煤層氣微地震檢測研究

張 巖 ，劉小秋 ，宋利偉 ，董宏麗

（1.東北石油大學 計算機與信息技術學院，黑龍江 大慶 163318；2.東北石油大學 物理與電子工程學院，黑龍江 大慶 163318；3.東北石油大學 人工智能能源研究院，黑龍江 大慶 163318；4.黑龍江省網絡化與智能控制重點實驗室，黑龍江 大慶 163000）

與常規碳酸鹽、砂巖儲層相比，我國大多數煤礦地質條件復雜、各向異性較強、吸附態高、煤層滲透率低，幾乎都需要通過水力壓裂進行儲層改造[1]。微地震監測技術是檢測壓裂效果，把煤層氣開采與原煤開采結合起來的重要環節，是一個不可忽視的技術。利用該技術能清楚地認識到煤層氣壓裂井的空間展布形態、幾何參數、延伸方位以及隨時間變化的特征[2]，能更好地監測煤層壓裂裂縫的發育方向和空間展布特征，可以提高找尋煤層氣氣藏的效率、縮短和降低儲層檢查測的周期與費用[3]。

煤層氣微地震信號受地面噪聲和地層的吸收衰減影響，信噪比普遍較低[4]。壓制噪聲是提高檢測準確率的普遍思路[5-8]。此類在事件識別前進行相應濾波、去噪算法的方法，一般基于某種先驗或通過建立數學模型來刻畫噪聲特征并加以去除，往往會損壞原始信號中代表有效事件的隱藏特征引起檢測錯誤，從而導致煤層氣裂縫和孔隙發育的誤判。因此研究直接從監測資料中檢測微地震的方法至關重要。此類方法的原理是根據微地震事件與噪聲特征的明顯差異，進行聚類或分類處理，在微地震事件信號能量較強的情況下具有一定的效果，但是煤層氣微震往往震級較小，且受噪聲影響嚴重，需要研究一種適應于煤層氣微地震噪聲大、震級小的高精度自動檢測方法[9-11]。

目前，深度卷積神經網絡已經在各個領域取得了顯著的應用效果，但由于網絡對樣本質量要求較高，限制在煤層氣勘探和開發中的應用[12-13]。因此，提出一種基于多尺度神經網絡的煤層氣微地震事件檢測方法，在深度卷積神經網絡模型中引入不確定理論中的可信度（Certainty-Factor，C-F）模型，首先用地下介質模型構建訓練數據集，然后用實際數據測試模型性能。通過多尺度卷積神經網絡提取微地震信號的淺層波形特征和深層語義特征，利用不同尺度的特征進行可信度建模得到各個尺度檢測置信度。最終檢測結果通過可信度模型進行不確定性的信任度融合，得到的結果具有更高的置信度。

1 原理方法

1.1 多尺度特征

傳統檢測網絡結構中，檢測器通常接入卷積神經網絡最后1 層進行預測，深層特征圖無法提供細粒度的信息，尋求多尺度上的特征表達是解決細粒度丟失的有效辦法[14]。因為卷積神經網絡層層相疊的結構，特征圖越深，感受野越大。因此，網絡內不同深度的特征圖就形成了特征圖的多尺度表達。SSD 算法和 MS-CNN 算法提出直接在不同尺度的特征圖上分別檢測目標，最后進行整合的思想。其中淺層特征圖負責檢測識別細節目標，深層特征圖負責檢測主體目標。

傳統網絡在得到高尺度特征圖后，在最后1層進行預測。多尺度檢測網絡不僅可以得到不同尺度的特征圖，還對不同尺度的特征圖進行預測。不同尺度的特征圖分配權重進行加權融合處理時，總體損失函數E表達如下：

式中：l為 不同的尺度；L為尺度的總量； ωl為尺度l損失的加權因子；El(αl)為尺度l的損失； αl為尺度l的特征圖。

尺度l的損失大小受該尺度特征圖影響，該尺度特征圖與相應的卷積核和偏置有關。用f(·)表示加權方式，式（1）可以寫成：

式中：Kl為尺度l的卷積核；bl為尺度l的偏置項。

1.2 可信度模型

神經網絡在分類時輸出類別置信度分數，通常通過對置信度進行閾值判別預測結果，此類判別方法往往不利于網絡表達知識的不確定性。可信度模型可以結合各個尺度的置信度分數，經過不確定性推理得到融合結果，是一種有效的不確定性推理方法。結合該模型將神經網絡各個尺度的檢測結果作為證據，最終識別結果作為結論，每個尺度的檢測結果和最終結果的關系為知識，知識不確定性可以用產生式規則表示為：

式中：CF(H,Ei)為可信度因子（靜態強度）表示知識的強度，即當Ei所對應的證據為真時，Ei對H的影響程度為CF(H,Ei)。

模型中用于微地震事件檢測時，式（3）的含義為：在尺度i上檢測為微地震事件時，確實為微地震事件的可信度為CF(H,Ei)。相關證據的出現提高結論H為真的可信度，則CF(H,Ei)＞0，表示證據的出現支持H為真，會使CF(H,Ei)的值變大；反之CF(H,Ei)＜0，表示證據的出現支持H為假，CF(H,Ei)的值則會變小；CF(H,Ei)=0，表示證據的出現與結論無關。靜態強度由先驗概率P（H）和后驗概率P(H|Ei)求出，但是在實際應用中，先驗概率和后驗概率很難獲得，一般情況下靜態強度直接由專家直接給出，原則是相應的證據的出現越是支持H為真，CF(H,Ei)就應該越大；反之，則越小。

模型將知識和證據的不確定性通過逐步推理傳遞給結論。結論H由Ei所對應的證據推理得到的可信度表示為CFi(H)，由下式計算：

式中：CF(Ei)為動態強度，表示證據Ei當前的不確定性程度。

分別求出每個尺度上檢測為微地震事件的可信度，然后用結論不確定性算法合成最終結論的可信度，最終結論的可信度綜合了多個尺度上知識的不確定性，在一定程度上可以提高檢測的準確性。用CFi,j(H)表示Ei和Ej綜合影響所形成的可信度，結論不確定性算法[17]如下：

當CFi(H)＜0，CFj(H)＜0時：

2 多尺度檢測模型

2.1 模型構建

多尺度檢測神經網絡模型結構如圖1。采用4個檢測尺度，每個檢測尺度分別由卷積、歸一化、激活函數組成。每個尺度后分別與對應的檢測器相連，檢測器由3 個池化層和3 個全連接層交替組成，檢測器把結果輸入C-F 模型中進行決策。地震事件檢測屬于二分類問題，盲目加深網絡會加大模型存儲，還可能導致在求解最優解過程中梯度消失；模型隨著卷積神經網絡的加深，逐步減少卷積核的大小，提高細粒多尺度表達。

圖1 模型結構Fig.1 Model structure

多尺度網絡檢測是建立在對多尺度特征圖的獨立識別上的，樣本檢測的最終檢測結果通過標簽進行監督訓練。原始數據經過預處理得到樣本和標簽，經過預處理的樣本通過多尺度網絡進行多尺度特征圖的提取，多尺度特征圖送入檢測器進行檢測，并計算每個尺度的精確度。將每個尺度檢測得到的置信度作為動態強度、精確度作為靜態強度送入可信度模型，得到最終的合成結果，最終合成結果與標簽計算損失誤差和各項評價指標。

2.2 實驗數據

實驗數據分為正演數據和實際數據。正演實驗用理論地下介質模型，模擬實際煤層氣壓裂數據。實際數據為黑龍江某地區的實際監測數據。

正演速度模型如圖2。正演模型尺寸為4 000 m×4 000 m，將其劃分為10×10 的網格點，其中下層介質速度為5 000 m/s，厚度為2 600 m，上層介質速度為3 000 m/s，厚度為1 400 m。模型中心（2 000，2 000）為水力壓裂震動裂縫。在地表每隔10 個網格點布置1 個檢波器，對裂縫產生時的震動進行監測。

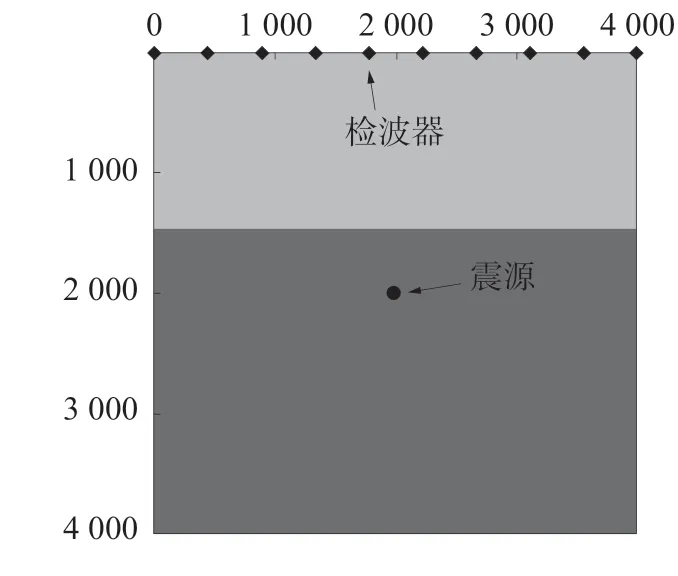
圖2 正演速度模型Fig.2 Forward velocity model

實際監測地區的介質特性如下：儲層孔隙度7.5%～17.6%，滲透率0.15×10-3～4.94×10-3μm2。孔隙度主要分布在12%～16%范圍，滲透率主要分布在0.1×10-3～1.5×10-3μm2范圍。平均孔隙度為13.9%，平均滲透率為1.23×10-3μm2。

正演介質模型較實際地質情況相對簡單，添加的噪聲通過高斯隨機噪聲模擬。實際數據中噪聲來自真實環境背景噪聲，更為復雜、更容易誤檢。正演數據和實際數據的采樣周期需要保持一致，以保證樣本能包含完整的微地震事件特征。

采用滑動窗口的方法進行數據擴增和解決訓練過程中樣本均衡的問題，以適應神經網絡對樣本的要求。滑動窗口處理數據如圖3。a為滑動窗口長度，s為滑動步長，L為數據的總長度。

圖3 滑動窗口處理數據Fig.3 Sliding window processing data

樣本使用獨熱編碼，含微地震事件為正樣本標注為1，只含背景噪聲的為負樣本標注為0。獲得的樣本總量n為：

檢波器接收微地震數據時，大部分都是背景噪聲，有效波形只占小部分，得到的正樣本的量遠少于負樣本的數量，隨機去掉部分負樣本使得正、負樣本數量相當。正演數據中單道微地震信號檢波器采樣點為1 0000，滑動窗口長度設置為100、步長設置為20，可以得到數據9 995 個樣本，其中包含微地震事件的樣本為245 個。舍去多余負樣本后，相比單純設置長度100 分割數據的方法，擴增了4.9 倍。

2.3 模型訓練

網絡構建全局損失函數，在神經網絡訓練過程中，以損失為優化目標反向傳播誤差，調節卷積核參數。用二值交叉熵（Binary Cross Entropy ,BCE）損失函數，定義如下：

式中：C為樣本個數；為第i個樣本的標簽；y為第i個樣本的預測值。

訓練集包含4 000 個樣本，批量大小設為200，迭代次數設置為500，學習率設為0.01，最后保存調整好的網絡參數。模型采用Python 語言和Pytorch 框架作為編程環境。實驗在配備Intel Core i7 9700k 處理器和32G 內存的計算機上運行。訓練和測試過程中的模型損失和準確率曲線如圖4。

圖4 模型損失和準確率曲線Fig.4 Model loss curves and accuracy curves

由圖4 可知：在迭代40 次后訓練損失和測試損失都下降不明顯，準確率和損失在后60 個迭代中改變都很小，損失最終下降到0.054，準確率最終達到98%，模型收斂。

3 實驗結果

3.1 正演信號模型

考慮到微地震信號采集實際過程中受環境和設備等不確定性因素的影響，將測試集樣本中加入不同強度噪聲輸入性能良好的網絡中。不同信噪比正演信號如圖5，模型檢測結果見表1。

表1 模型檢測結果Table 1 Detection results of model

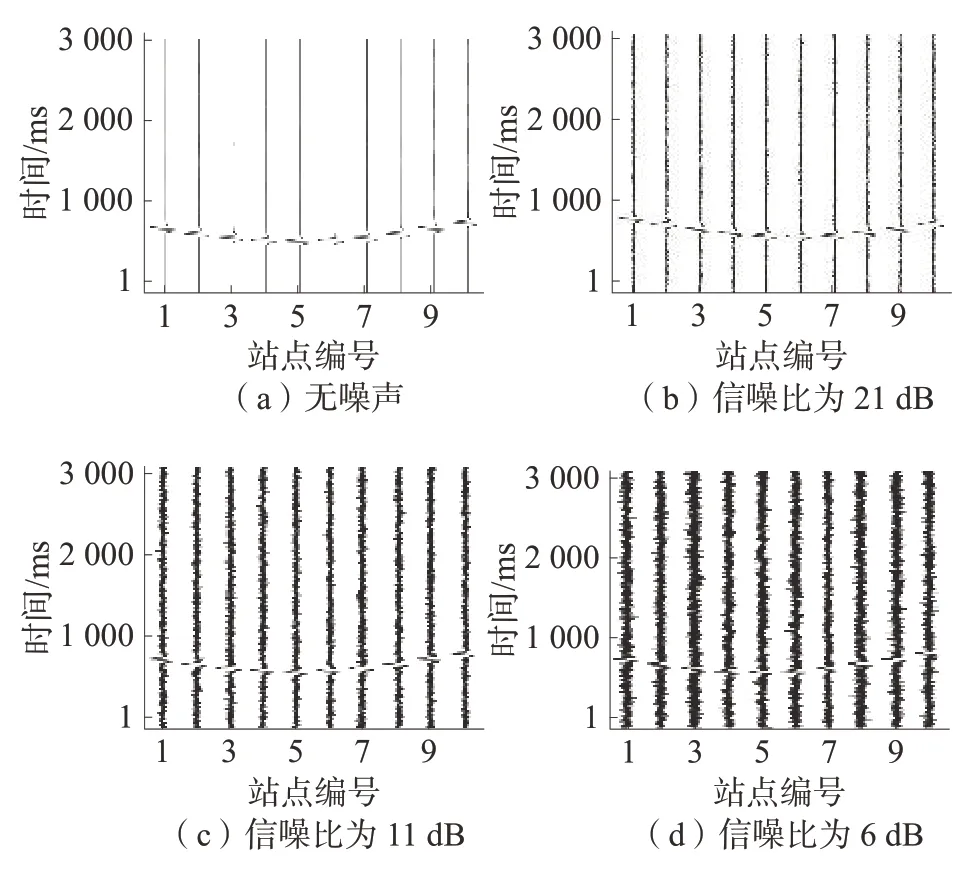
圖5 不同信噪比正演信號Fig.5 Simulation signal with different SNR

由圖5 可知：隨著信噪比減小，噪聲污染愈加嚴重，甚至幾乎淹沒有效信號。當無噪聲以及加入噪聲后信噪比為21 dB 時，微地震事件清晰可見；當加入噪聲后信噪比為11 dB 時，噪聲開始明顯影響有效信號；當加入噪聲后信噪比為6 dB 時，有效信號完全淹沒在噪聲中，肉眼難以甄別。

由表1 可知：800 個測試樣本中包含微地震波形的正樣本為400 個；當無噪聲干擾時得到TP 和FN 均為400，即包含微地震波形的樣本和不包含微地震波形的樣本都全部被無誤地檢測出來。隨著信噪比降低，噪聲干擾越來越大，越多正樣本被噪聲淹沒，檢測結果的準確率也逐漸降低。正演數據檢測結果如圖6。

圖6 正演數據檢測結果Fig.6 Detection results of forward data

為驗證本文模型的性能，對比不同方法對微地震波形的檢測能力，分別用小波分析法、BP 網絡、CNN 網絡和本文提出的多尺度檢測神經網絡對不同信噪比的微地震資料進行檢測。不同噪聲強度下的準確率如圖7。

圖7 不同噪聲強度下的準確率Fig.7 Accuracy under different SNR

由圖7 可知：本文模型結合了多尺度特征，檢測效果最好，甚至在無噪聲污染（信噪比為30 dB）時，準確率可以達到99.99%；輕微噪聲污染（信噪比為21 dB）時，準確率可以達到97.38%。

為了更客觀地評價模型的檢測效果，引入評價指標精確率P和召回率R，其定義如下：

不同方法在不同噪聲強度下的精確率見表2。不同方法在不同噪聲強度下的召回率見表3。

表2 不同方法在不同噪聲強度下的精確率Table 2 Accuracy rates of different methods under different noise intensities

表3 不同方法在不同噪聲強度下的召回率Table 3 Recall rates of different methods under different noise intensities

由表2、表3 可知：在無噪聲污染的情況下，4 種方法的精確率和召回率都在0.94 以上；隨著噪聲干擾變大，精確率和召回率都呈不同趨勢下降。總體上4 種方法都呈現出精確率和召回率隨噪聲干擾增大而減少。且3 種深度學習的方法的精確率和準確率都是由BP 模型、CNN 模型、本文模型逐漸升高。小波分析法的精確率和召回率受所設定閾值影響，閾值越大，越多正樣本無法被檢測到，閾值越小，越多負樣本被誤檢。在樣本上經過反復實驗，閾值選取為0.13，此時只有極少的負樣本被檢測為正例，精確率較高，但是有部分正樣本被檢測為負例，模型召回率較低。

3.2 實際信號檢測結果

由于煤層厚度、泊松比、滲透率、孔隙率等差異，不同區域的煤層氣微地震波形所含噪聲差異很大，同一地區因為設備和作業環境采集的微地震數據也會有很大的差異。壓裂井的部分監測實際數據如圖8，每組數據有27 道，每道為32 000 個采樣點，其中，微地震事件的信噪比主要集中在2～6.8 dB，能級主要集中在-3.26～-1.82之間。實際數據檢測結果如圖9。

圖8 實際數據Fig.8 Actual data

圖9 實際數據檢測結果Fig.9 Actual data detection results

利用網絡對實際波形數據進行微地震事件檢測，結果表明：本文方法能有效判別微地震事件，因此具有良好的檢測能力。

4 結 語

1）模型利用神經網絡有高度非線性的特點，綜合微地震信號的多尺度特征來進行信號自動識別，具有準確、快速、無需設定閾值等優點。

2）用準確度、精確率、召回率評價模型檢測能力，在煤層氣微地震信號信噪比大于6 dB 的情況下，模型檢測準確度大于91.13%，精確率達到92.1%以上，召回率能達到90%以上。

3）黑龍江某地區實際監測數據驗證顯示，模型能有效地檢測出微地震事件時間段。在煤層氣開采過程中，通過對煤層氣微地震資料進行事件的精確檢測對后續反演、裂縫監測有很重要的意義。