基于改進非洲禿鷲優化算法的圖像閾值分割研究

張嘯宇, 方忠慶, 杜 義, 孔維賓, 王玉婷, 程子耀

(鹽城工學院信息工程學院, 江蘇 鹽城 224051)

0 引言(Introduction)

元啟發式算法是一類獨立于問題的優化算法,能夠有效探索一個搜索空間并找到全局最優解。這類算法主要通過模擬自然界優勝劣汰的規律以及生物行為,實現種群的整體進步,最終求解最優解。典型算法有遺傳算法(GA)[1]、差分進化算法(DE)[2]、粒子群算法(PSO)[3]、灰狼算法(GWO)[4]、鯨魚優化算法(WOA)[5]、金豺狼優化算法(GJO)[6]等。

按閾值對圖像分割是一種常用的圖像分割方法,目前國內外已經有很多學者將元啟發式算法用于圖像的閾值分割優化中。KHAIRUZZAMAN等[7]將灰狼優化算法應用于圖像的多級閾值分割,取得了很好的效果。于洋等[8]為了解決紅外相機采集行人圖片時圖像分割效果問題,提出一種自適應粒子群優化二維OSTU的閾值分割算法,能夠快速且準確地得到最佳閾值,提高了圖像預處理的分割效果。UPADHYAY等[9]將Kapur熵作為適應度函數,并通過烏鴉搜索算法求得最大Kapur熵,達到最優閾值。

非洲禿鷲算法(AVOA)[10]是受非洲禿鷲覓食和導航行為啟發而提出的高性能智能算法,具有求解精度高的優點,但其全局搜索能力弱、易陷入局部。本文通過分段線性混沌映射(PWLCM)進行種群初始化,增強種群多樣性;在全局搜索階段引入β分布更好地控制種群在搜索空間上的重新劃分;提出了新的基于饑餓率的全局搜索策略,用于增強算法搜索能力。將改進算法運用在二維Otsu圖像閾值分割任務中取得了不錯的效果。

1 基礎非洲禿鷲優化算法(Basic African Vulture Optimization Algorithm)

非洲禿鷲優化算法(AVOA)是通過對非洲禿鷲的覓食行為和生活習慣進行模擬和建模而提出的。在AVOA中,非洲禿鷲的生活習慣和覓食行為主要包括以下4個階段。

1.1 階段一:隨機選擇最佳禿鷲

初始化種群后首先計算種群的適應度,其次選擇最優個體為最優禿鷲,選擇次優個體作為次優禿鷲。每次的最佳禿鷲會在這兩個個體中通過如下公式計算產生,同時在每次更新迭代后重新計算整個總體。

(1)

其中,L1和L2為搜索操作之前給定的參數,其值介于0～1且兩個參數之和為1。選擇最優解的概率pi使用如下公式的輪盤賭方式獲得,并為每組選擇最優解。

(2)

1.2 階段二:計算禿鷲的饑餓率

禿鷲的饑餓率由如下公式計算得出:

(3)

(4)

其中,F表示禿鷲的饑餓率,l表示當前的迭代次數,maxiterations表示最大迭代次數,z為介于-1～1且每代變化的隨機數,h是介于-2～2的隨機數,rand1是介于0～1的隨機數。

同時,當F的絕對值大于1時,算法進入探索階段;當F的值小于或等于1時,算法進入開發階段。

1.3 階段三:探索

AVOA的探索階段禿鷲有兩種不同的搜索策略,在兩組最佳禿鷲之一的周圍區域尋找食物和根據其饑餓程度在環境中隨機搜索。

P(i+1)=R(i)-D(i)×F

(5)

D(i)=|X×R(i)-P(i)|

(6)

公式(5)模擬了在兩組最佳禿鷲之一的周圍區域尋找食物,其中P(i+1)為下一次迭代的位置,F是由公式(4)計算得出的禿鷲的饑餓率,R(i)是由公式(1)給出的最佳禿鷲,D(i)為到兩組最佳禿鷲之一的隨機距離,通過公式(6)計算得到。在公式(6)中,R(i)是由公式(1)給出的最佳禿鷲。X被用作增加隨機運動的系數向量,由X=2×rand計算得到,其中rand為介于0～1的隨機數。P(i)為當前禿鷲的位置。

P(i+1)=R(i)-F+rand2×((ub-lb)×rand3+lb)

(7)

公式(7)模擬了禿鷲根據其饑餓程度在環境中隨機搜索,其中rand2是介于0～1的隨機值,lb和ub表示變量的上界和下界,rand3是用于增加隨機性的系數。

這兩種策略會根據P1的值進行選擇,P1是介于0～1的數。設randP1為介于0～1的隨機數。如果randP1的值小于或等于P1,則使用公式(5),反之,使用公式(7)。

1.4 階段四:開發

1.4.1 開發(第一階段)

當F的絕對值介于0.5～1時,AVOA進入開發階段的第一階段。在開發階段的第一階段,執行緩慢圍攻和旋轉飛行兩種不同的策略。

(1)緩慢圍攻:當|F|≥0.5時,禿鷲相對能量充足。當許多禿鷲聚集在一個食物源上時,會在食物獲取上引起嚴重的沖突。身體強壯的禿鷲不喜歡分享食物,而弱小的禿鷲試圖聚集并引發小沖突以便獲取食物,如下兩個公式模擬了這兩個過程。

P(i+1)=D(i)×(F+rand4)-d(t)

(8)

d(t)=R(i)-P(i)

(9)

公式(8)中,D(i)為到兩組最佳禿鷲之一的隨機距離,通過公式(6)計算得出,rand4為介于0～1的隨機值。公式(9)中,R(i)是在當前迭代中使用公式(1)選擇的最佳禿鷲。

(2)旋轉飛行:禿鷲經常進行旋轉飛行,可用于模擬螺旋運動。所有禿鷲與最佳和次佳禿鷲中的一只建立了一個螺旋方程,公式如下所示:

(10)

(11)

P(i+1)=R(i)-(S1+S2)

(12)

其中,rand5和rand6是介于0～1的隨機數,最后通過公式(12)更新禿鷲的位置。

這兩種策略會根據P2的值進行選擇,P2是介于0～1的數。設randP2為介于0～1的隨機數。如果randP2的值小于或等于P2,則根據公式(8)實施緩慢圍攻策略,反之,使用公式(12)執行旋轉飛行策略。

1.4.2 開發(第二階段)

當|F|<0.5時,AVOA進入開發階段的第二階段,禿鷲開始進行聚集圍攻和爭奪食物。

(1)幾種禿鷲在食物源上的聚集。

描述禿鷲這種運動的公式如下所示:

(13)

(14)

(15)

公式(13)和公式(14)中,BestVulture1(i)是當前迭代中第一組的最佳禿鷲,BestVulture2(i)是當前迭代中第二組的最佳禿鷲。用公式(15)計算得到下一代禿鷲的位置P(i+1)。

(2)對食物的激烈競爭。

當|F|<0.5時,領頭的禿鷲變得饑餓和虛弱,沒有足夠的能量對抗其他禿鷲。而其他禿鷲會從不同方向朝著領頭禿鷲的位置移動,可以使用如下公式模擬該現象:

P(i+1)=R(i)-|d(t)|×F×Levy(d)

(16)

其中,d(t)表示禿鷲與兩組中最佳禿鷲之間的距離,該距離通過公式(9)計算得出。萊維飛行機制用于提高公式(16)中AVOA算法的有效性,萊維飛行生成的隨機分量用以下公式計算。

(17)

其中

(18)

公式(17)、公式(18)中,α為固定值1.5。u和v服從正態分布:

(19)

第二階段的兩種策略會根據P3的值進行選擇,P3是介于0～1的數。設randP3是介于0～1的隨機數,如果randP3小于或等于P3,則根據公式(15)更新位置;反之由公式(16)實施對食物的激烈競爭。

2 改進非洲禿鷲優化算法(Improved African Vulture Optimization Algorithm)

針對非洲禿鷲算法全局搜索能力不足、局部搜索策略冗余及收斂速度慢等缺點,β-PAVOA主要做了以下改進。

2.1 基于PWLCM混沌映射的種群初始化

混沌映射是生成混沌序列的一種方法,被廣泛地應用于各種算法中。PWLCM[11]作為混沌映射的典型代表,其數學形式簡單,具有遍歷性和隨機性。如圖1所示,PWLCM在空間中的分布非常均勻。

(a)PWLCM混沌映射圖

通過PWLCM初始化種群,可以使β-PAVOA在初始化種群時更好地搜索整個解空間。PWLCM映射的描述如公式(20)所示:

(20)

公式(20)中,PZ=0.4,如果t≥2,則z(t)值可根據公式(20)計算得到,如果t=1,則z(1)為映射的初始值,z(1)取值是介于0～1的隨機數。

將生成的值映射到解空間,如下公式所示:

P(i)=(ub-lb)×z(i)+lb

(21)

其中,P(i)是映射后的種群位置,ub和lb分別是位置的上界和下界,z(i)是由公式(20)得到介于0～1的混沌映射隨機值。

2.2 基于β分布的全局增強搜索策略

β分布[12]是指一組定義在區間[0,1]的連續概率分布。在使用元啟發式算法解決工程問題時,將β分布用于其中很有效,它可以近似模擬包括正態高斯分布在內的幾種分布,也允許近似線性或指數遞減的分布,可以是一維的,也可以是多維。一維β分布表達式如下:

(22)

(23)

其中,通過改變參數p和q就可以得到可能的β分布的多樣性。基于β分布的全局增強搜索策略如公式(24)所示:

P(i+1)=(ub-lb)×betarand+lb

(24)

其中,P(i+1)為更新后的位置,betarand是p=1、q=1的情況下生成的β隨機數。

2.3 基于饑餓率F的改進搜索策略

在測試過程中發現,AVOA在探索階段的全局搜索表現不佳,因此提出了基于禿鷲饑餓率的改進搜索策略如公式(25)所示,用于改善這一問題。

P(i+1)=(rand-F)×X(randi(1,pop_size))

(25)

其中,P(i+1)為更新后的位置,rand為介于0～1的隨機值。X為種群的歷史最優位置,randi(1,pop_size)為1至種群大小之間的隨機整數值。

2.4 改進局部搜索策略

β-PAVOA針對局部搜索策略冗余、收斂慢的缺點,對開發階段策略進行了精簡,整個開發階段只使用AVOA在開發階段的第二階段中的更新策略,rand是介于0～1的隨機數。如果rand小于0.3,則根據公式(15)更新位置;反之由公式(16)實施對食物的激烈競爭。β-PAVOA的算法流程如圖2所示。

3 實驗仿真與結果分析(Experimental simulation and result analysis)

3.1 實驗環境設置

β-PAVOA在8個基準測試函數上進行了測試,選取了非洲禿鷲算法(AVOA)、金豺狼優化算法(GJO)、灰狼算法(GWO)、鯨魚優化算法(WOA)和粒子群算法(PSO)作為對比算法。測試函數分為兩類:F1～F4為單峰函數,F5～F8為多峰函數,測試函數設置見表1,算法默認參數設置見表2。將測試結果進行秩和檢驗,確定β-PAVOA獲得結果的平均值與對比算法之間是否存在顯著差異,當ρ>0.05時,認為β-PAVOA與對比算法的尋優性能相當。種群大小設置為50,最大迭代次數為1 000次,測試維度為30。為了減少不確定性,每個測試獨立進行30次,計算30次測試的平均數和方差。實驗是在配備32 GB RAM與i7-12700H處理器的個人計算機上進行的。

表1 測試函數設置Tab.1 Benchmark function settings

表2 算法參數設置Tab.2 Algorithm parameter settings

3.2 精度與收斂性分析

β-PAVOA與其他算法的測試結果見表3和表4。在F1～F8上,β-PAVOA展現出了極強的優勢,從表3和表4中可以看出,相比其他算法在F3、F4、F7、F8上的測試結果,β-PAVOA有著領先幾個量級的精度,在F1、F2、F5、F6上的測試結果相近的情況下,其穩定性有著明顯的優勢。同時,從圖3和圖4中的算法收斂曲線可以明顯看出,β-PAVOA在F1～F8上的收斂精度與收斂速度均優于其他算法。

表3 各類算法在 F1～F4上的測試結果Tab.3 Test results of various algorithms on F1～F4

表4 各類算法在F5～F8上的測試結果Tab.4 Test results of various algorithms on F5～F8

(a)F1函數的收斂對比曲線

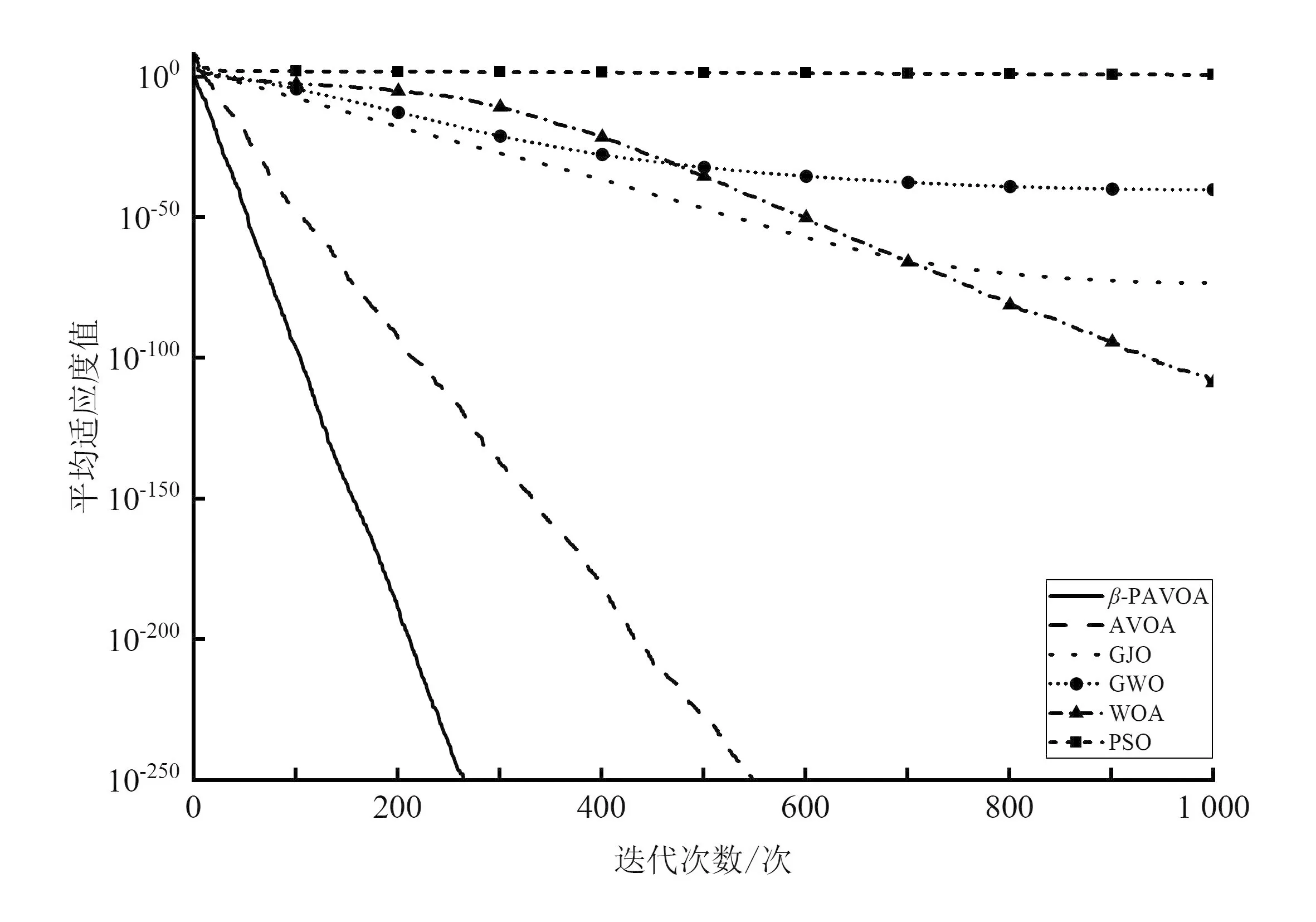
(b)F2函數的收斂對比曲線

(c)F3函數的收斂對比曲線

(d)F4函數的收斂對比曲線圖3 不同算法的F1～F4收斂曲線對比Fig.3 Comparison of convergence curves of different algorithms on F1～F4

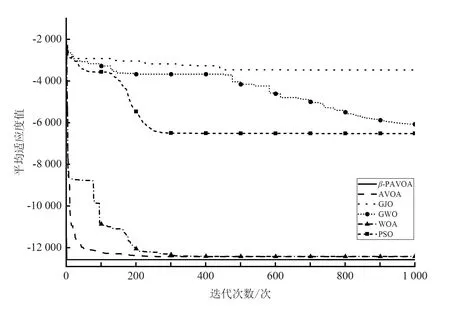
(a)F5函數的收斂對比曲線

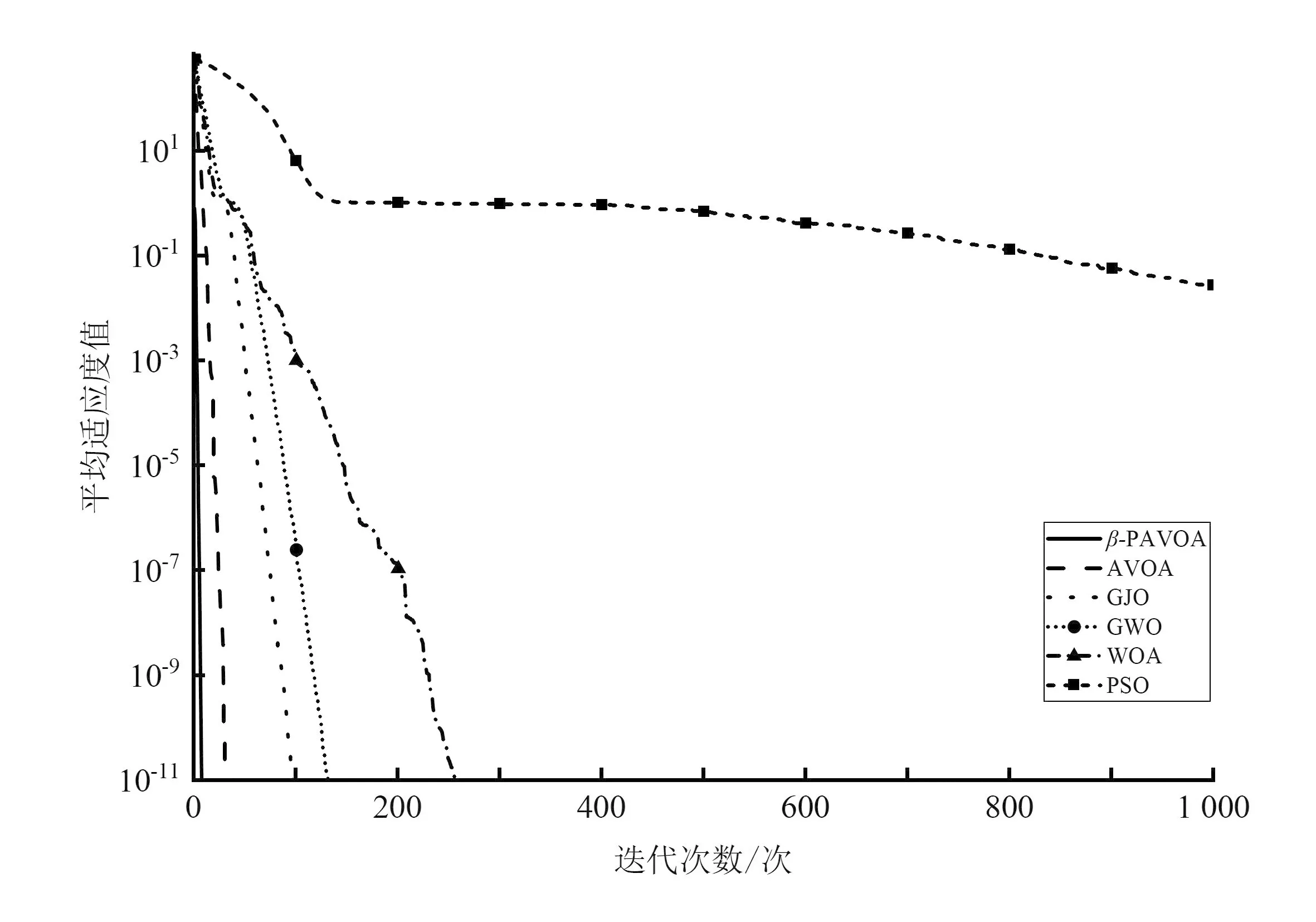
(b)F6函數的收斂對比曲線

(c)F7函數的收斂對比曲線

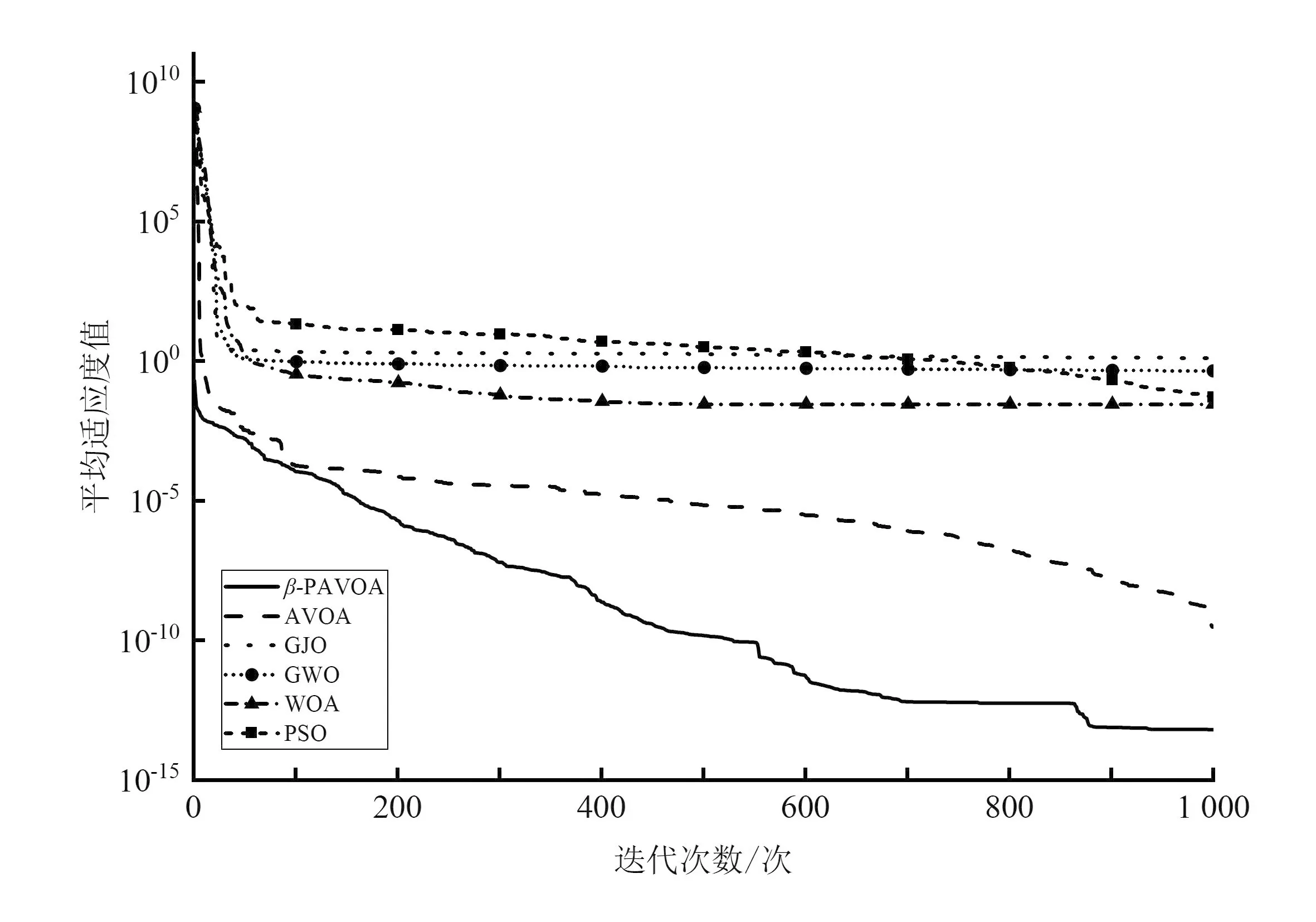
(d)F8函數的收斂對比曲線圖4 不同算法的F5～F8收斂曲線對比Fig.4 Comparison of convergence curves of different algorithms on F5～F8

4 Otsu圖像閾值分割(Otsu image threshold segmentation)

Otsu閾值分割常用于圖像二值化或閾值化[13]。圖像閾值化是將灰度圖像轉換為二值圖像的過程,其中每個像素根據特定的閾值被賦予黑色或白色值。Otsu閾值分割法簡單高效,適用于分割、目標檢測和特征提取[14]。Otsu閾值分割法在具有雙峰直方圖的圖像上效果最好,即圖像中有清晰的表示背景和前景像素強度的峰值。對于具有更復雜分布的圖像,其他閾值化方法或更高級的技術可能更合適。

Otsu閾值分割法是找到能夠使類間方差最大化的閾值,從而有效地將像素分為兩個類別:前景和背景。類間方差測量兩個類之間的擴展或可分性,并根據圖像中的像素強度和概率計算。

4.1 Otsu閾值分割

假設圖形大小為M×N,圖像灰度范圍為[0,L-1],ni為圖像灰度級i的像素點數,則灰度級i出現的概率為pi=ni/(M×N)。在單閾值分割模型中,圖像被分割成兩類,其中C0類像素點灰度級為[0,T],C1類像素點灰度級為[T+1,L-1]。P0(T)、P1(T)分別為C0、C1出現的概率,u0(T)、u1(T)分別為C0、C1的平均灰度級,由如下公式計算得出:

(26)

(27)

(28)

(29)

(30)

(32)

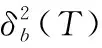
4.2 Otsu多閾值分割

(33)

(34)

(35)

(36)

(37)

圖像的類間方差用公式(36)表示,公式(37)則是最終的目標函數。

4.3 二維Otsu模型測試結果及分析

在二維Otsu模型測試中測試了β-PAVOA及對比算法的性能表現,測試選取了2張常用測試圖片與1張內容復雜的圖片(如圖5所示)。測試結果如圖6所示,β-PAVOA在找到最優解時,收斂速度與穩定性相比其他算法有明顯的優勢,這也驗證了優化策略的有效性。

(a)相機

(b)人像

(c)月球圖5 測試用圖Fig.5 The text pictures

(a)相機二維Otsu測試結果

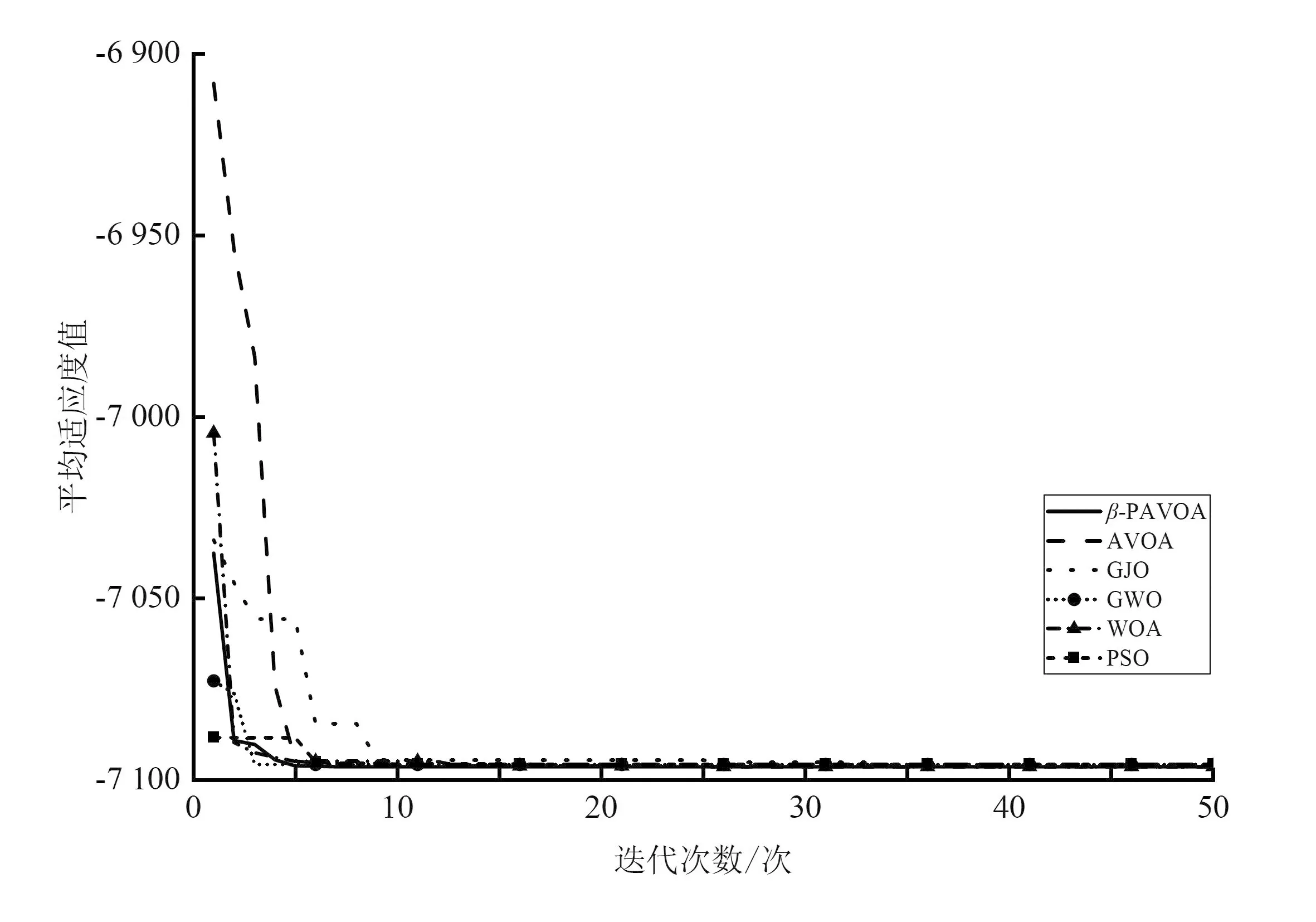
(b)相機二維Otsu模型迭代曲線

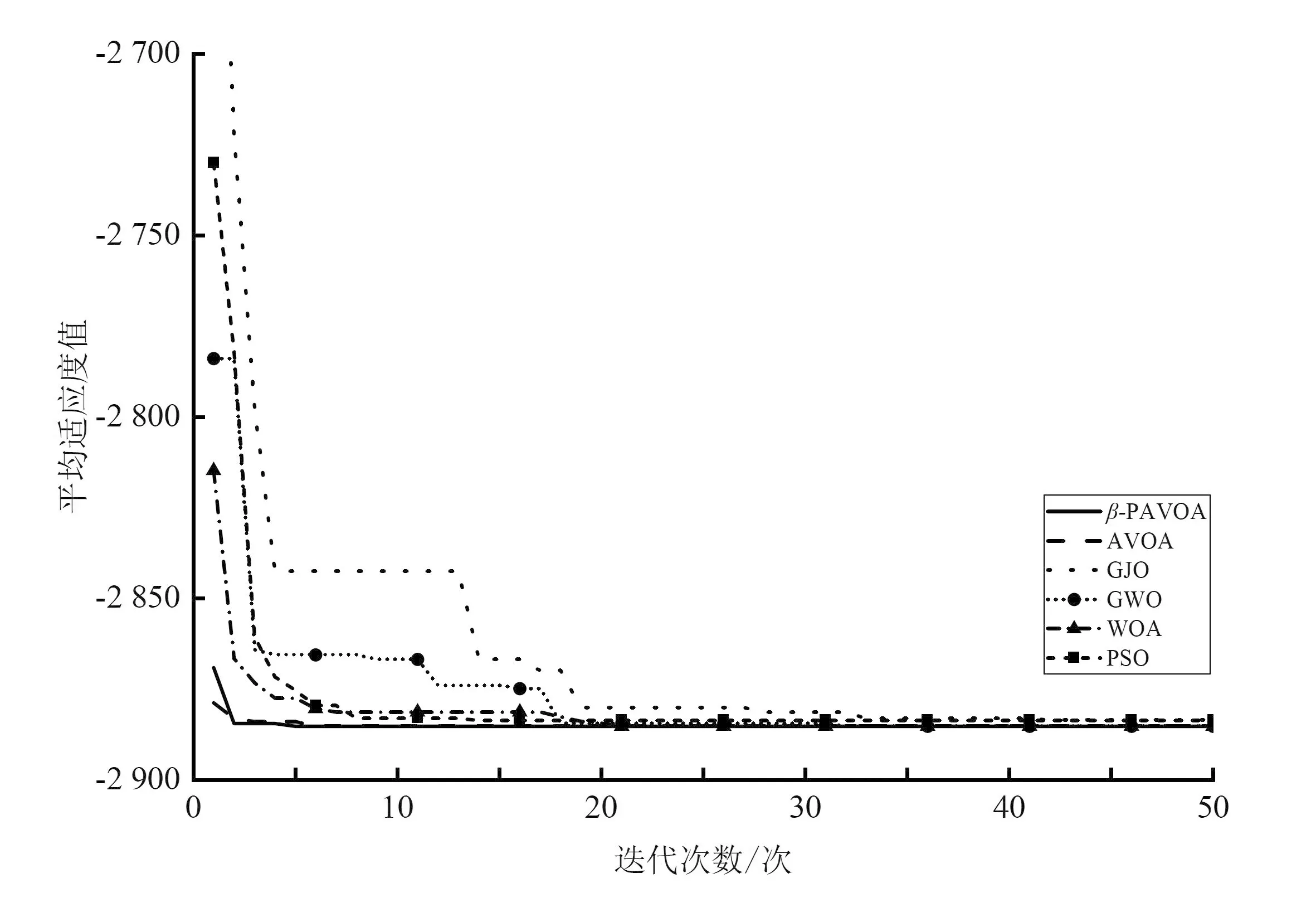
(d)人像二維Otsu模型迭代曲線

(e)月球二維Otsu測試結果

(f)月球二維Otsu模型迭代曲線圖6 測試結果圖Fig.6 The test results graph

5 結論(Conclusion)

本文提出了一種基于PWLCM與β分布的非洲禿鷲算法β-PAVOA。首先,通過PWLCM擴大種群在解空間的覆蓋程度,提高尋優能力。其次,使用基于β分布的全局增強搜索策略增強算法的全局搜索能力。基于饑餓率F的改進搜索策略進一步增強了全局搜索能力。最后,通過簡化局部搜索策略提升局部收斂速度。為了驗證β-PAVOA的有效性,通過8個基準測試函數和二維Otsu圖像閾值分割模型與非洲禿鷲算法(AVOA)、金豺狼優化算法(GJO)、灰狼算法(GWO)、鯨魚優化算法(WOA)和粒子群算法(PSO)進行對比實驗,采用均值、標準差與秩和檢驗方法進行評估。結果表明,β-PAVOA算法在探索能力和求解精度上都有顯著優勢。