基于多分辨奇異值分解包和隨機森林的電能質量擾動分類研究

張家寧 羅月婉 郭林明 楊曉梅

1(四川大學電氣工程學院 四川 成都 610065)

2(成都飛機設計研究所 四川 成都 610041)

Random forest

0 引 言

隨著光伏發電和風力發電等新型能源以及電動汽車充電樁等非線性負載在電網中的接入,電網中的電能質量問題日益嚴重[1]。為了滿足用電設備日益精密化的用電需求,需要對電能質量的單一和復合擾動進行準確識別,從而進行進一步的抑制和改善。

電能質量擾動(Power Quality Disturbances,PQD)[2]的分類本質是對存在PQD問題的信號先進行時頻域的變換進而特征提取,再通過特征選擇和分類進行故障信號的辨識。常見的用于PQD信號時頻域變化的方法主要有短時傅里葉變換(Short-Time Fourier Transform,STFT)[1]、經驗模態分解(Empirical Mode Decomposition,EMD)[3]、S變換(S Transform,ST)[4]、變分模態分解(Variational Mode Decomposition,VMD)[5]、離散小波變換(Discrete Wavelet Transform,DWT)[6]和小波包分解等。以上方法均被證明在一定使用條件下有較好的PQD問題分類能力,但是也存在一些不足:STFT對信號的瞬態特征捕捉效果欠佳;EMD存在易產生虛假分量的弊端;VMD計算復雜度較高,導致算法計算負擔重等。其中,小波包分解使用常用的小波基Daubechies小波、Haar小波、Symlets小波和Coiflets小波等,通過多層分解將原信號進行多分辨率分解從而實現信號中特征信息的精細提取并完成分類識別[7]。但由于小波包的小波基選取對分類效果影響較大,對小波基的選取研究還有待進行。另一方面,近年來奇異值分解(SVD)在信號處理、濾波算法設計和特征提取等領域均被廣泛應用[8],多分辨率SVD(Multi-Resolution SVD,MRSVD)被證明在微弱信號定位和復雜型號的弱故障特征提取領域效果均優于小波包的處理效果[9]。

鑒于此,本文受小波包分解信號的啟發,提出一種基于多分辨SVD包分解與隨機森林結合(MRSVD-RF)的PQD擾動識別算法。首先以多分辨SVD為工具,用類似小波包分解的形式,對PQD信號進行三層SVD包分解,再通過對分解后的分量子信號進行特征提取構成特征集,最后結合使用隨機森林模型進行PQD信號的分類。實驗表明,本文提出的算法對單一和復合擾動的PQD問題都有較好的分類效果。為了驗證本文算法的優越性,本文還對比了基于小波包分解的特征提取與隨機森林結合(Wavelet Packet and Random Forest,WP-RF)算法,并對不同的特征提取方式、分類器選取和特征值數量對PQD問題分類的影響都進行了討論。

1 基于多分辨率SVD包的PQD信號分解

本文提出的MRSVD信號分解算法是受小波包算法啟發,使用遞歸分解的形式將信號進行多層SVD分解從而實現多分辨率分析。通過對分解后的分量信號提取具有更高時頻分辨率的特征信息,完成對信號的精確分類識別。本文算法的信號分解方式參考小波包分解信號的方式,為闡明MRSVD分解算法的步驟,先行對小波包分解算法的思想進行說明。

1.1 小波包變換的信號分解分析步驟

小波變換是一種對信號進行時頻分析的變換方法,為了對信號進行有效的時頻域分析,小波包在小波變換的基礎上使用多分辨率分析的方法將信號的高低頻成分進行分解,通過構造低通濾波器和高通濾波器,得到原始信號的低頻系數(Approximate Coefficients)和高頻系數(Detail Coefficients)[10]。與小波變換只分解低頻系數不同,小波包變換將每層分解得到的新的低頻系數和高頻系數繼續分解,這樣通過多層次、多頻帶地將信號進行劃分,使算法兼顧信號的時頻分辨率,凸顯子信號中的信號特征。小波包實現信號多分辨率分解的步驟如下。

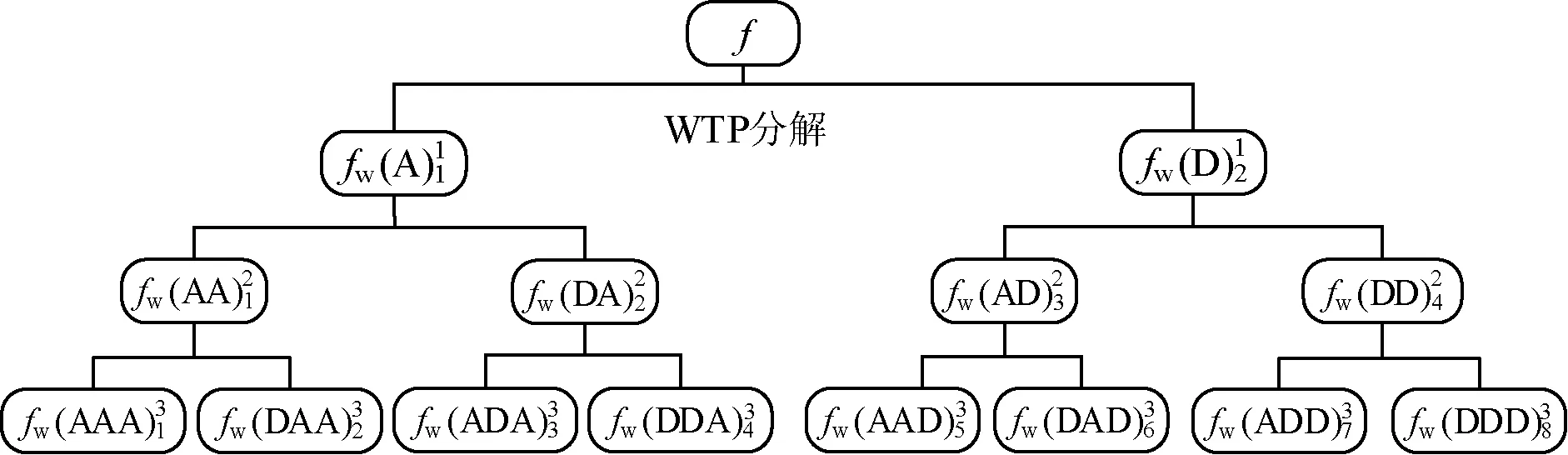
圖1 基于小波包變換的信號分解示例圖

通過圖1所示的結構對信號進行三層分解,實現了對信號的高低頻成分的細化體現。由圖可知,在對信號進行高、低頻段分解后,第三層的子信號和原始信號關系如式(1)所示,經過小波包分解后的信號利用濾波器的共軛矩陣,同一層的子信號可以通過求和得出原始信號,是小波變換方法的優勢之一。

f=fw(AAA)13+fw(DAA)23+fw(ADA)33+fw(DDA)43+fw(DDA)43+

fw(AAD)53+fw(DAD)63+fw(ADD)73+fw(DDD)83

(1)

以上對小波包分解算法實現原始信號的樹形分解過程進行了說明,為實現多分辨率SVD分解信號方式提供了參考意義。

1.2 利用SVD包變換的信號多分辨率分解原理

為了實現對PQD信號的分解,本文由1.1節小波包分解得到啟發,以SVD分解為工具,通過利用原始電壓信號構造矩陣,使用類似于小波包分解樹的信號分解方式,將PQD信號進行了多分辨率分解。經過分解后的分量子信號在擾動辨識時,可以從信號中獲取更多的特征信息。本文對電壓信號進行分解和處理,實現PQD問題的分類,多分辨率SVD包變換的PQD信號處理原理如下。

設電壓信號為U(t),經采樣后得到離散信號U(n),表示如下:

U(n)=[U1,U2,…,Un,…,UΖ]

(2)

式中:Z表示采樣總點數。

SVD分解需要以矩陣為計算對象,矩陣的構造方法直接影響SVD對信號處理的效果,為了對信號進行SVD分解,首先需要將信號U(n)構造成二維的Hankel矩陣形式:

(3)

對矩陣H進行SVD分解,有:

H=UΣVT

(4)

式中:U∈R2×2與V∈R(Z-1)×(Z-1)為兩個正交矩陣Σ=diag(αi),i=1,2,為一個大小為2×(Z-1)的對角矩陣且有α1≥α2,α1與α2對應矩陣H的兩個奇異值。

通過SVD分解,可以獲得一大一小兩個奇異值,可以設想,如果由二者分別求得兩個新的分量信號,再以兩個新的分量信號為基礎重新構造行數為2,形如式(3)的矩陣,就可以實現對第二層子信號的SVD分解,具體的分量信號重構與分解算法如下。

已知對由原始信號U(n)構造的矩陣SVD分解后的結果如式(4)所示,為了進行下一層SVD分解,將矩陣H用列向量u1∈R2×1和v1∈R(z-1)×1重寫,重寫后的矩陣H1與H2和矩陣H的關系如下:

(5)

H=H1+H2

(6)

式中:u1和u2分別為矩陣U的第1列向量和第2列向量;v1和v2分別為矩陣V的第1列向量和第2列向量。令H1=α1u1v1T,H2=α2u2v2T,此時H1對應原信號SVD分解后較大的奇異值,體現原信號的近似信號,H2對應原信號SVD分解后較小的奇異值,用以體現原型號中的細節信號,第三層信號的分解結果便由矩陣H1和H2的重構矩陣得來,方法如下:

顯然,此時矩陣Hi和矩陣H均為兩行Z列的矩陣,以矩陣H1為例,將其表示為:

(7)

通過類似于求兩行Hankel矩陣的逆變換的形式,即將矩陣的第一行元素與最后一列元素進行組合的方式進行待分解子信號的重構,記為f1,則有:

f1=[h1h2…hz-1hz]i=1,2

(8)

顯然,分量信號fi的數據元素完全繼承于H1,即與奇異值α1相對應,是第一層SVD分解后原始信號近似信號的體現。同理,用同樣的方式對矩陣H2進行重構可以得到反映原始信號細節信息的分量信號f2。至此,完成了對原始信號求取第一層分量子信號的任務,對應的分量子信號分別體現了原始信號的逼近信號和細節信號。

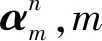
圖2 基于SVD包變換的信號分解示例圖

為了區分各層子信號的成分,使用字母a和d對子信號成分進行了標注:圖中d表示細節信號;a表示近似信號;上角標序列號表示分解的層數(即尺度);下角標序列號表示在該尺度的分解下子信號的序號數。通過上述方式的分解,原始信號在不同尺度下被分解為多個子信號。多分辨SVD包分解相較于小波包分解的優越性在于分解過程不會產生相位失真,因此在使用子信號對PQD信號進行辨識時能夠反映原始信號中擾動成分的真實大小。同時,此方法保留了小波包分解法滿足疊加原理的優點,原始信號的還原可以通過簡單的子信號求和得到,各尺度信號之間的關系如式(9)所示。

f=fs(a)11+fs(d)21=

fs(aa)12+fs(da)22+fs(ad)32+fs(dd)42=

fs(aaa)13+fs(daa)23+fs(ada)33+fs(dda)43+

fs(dda)43+fs(aad)53+fs(dad)63+fs(add)73+fs(ddd)83

(9)

為了直觀地體現SVD包分解對近似信號和細節信號的表現能力,對一段包含了信噪比為35 dB的高斯白噪聲,存在暫降幅值為0.6 p.u的電壓暫降PQD信號進行SVD包分解,如圖3所示。由圖可知,在對信號進行兩層SVD包分解后,信號信息在近似信號和細節信號中已有了明顯體現,細節信號還指示了擾動的起止點,并且通過SVD分解實現了對PQD信號的降噪處理。

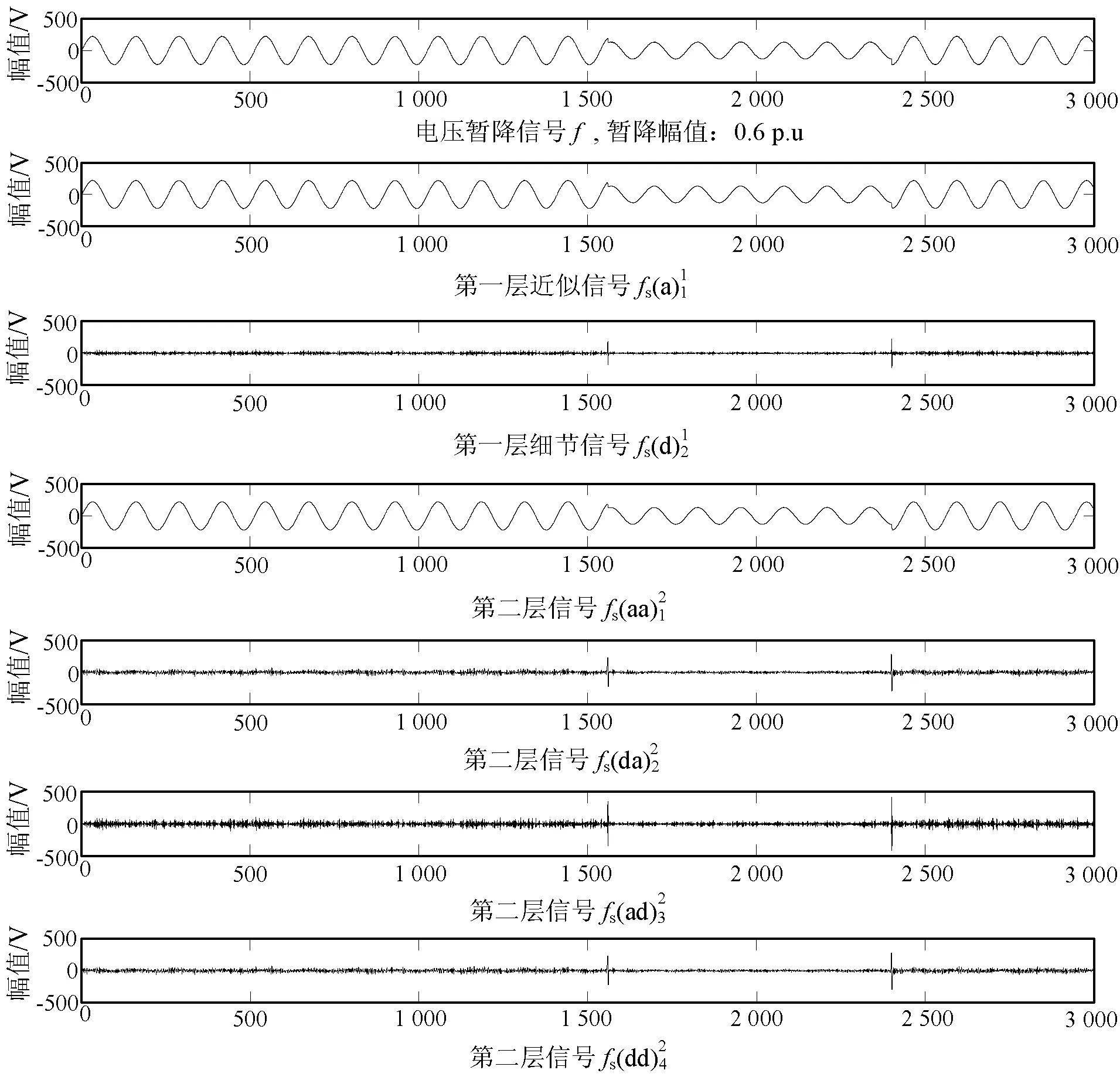
圖3 兩層SVD包分解電壓暫降信號實例圖

2 基于多分辨率SVD包分解的電能質量擾動識別

利用本文1.2節提出的MRSVD包對PQD信號進行分解為PQD問題分類的研究提供了特征提取基礎。本文提出的基于MRSVD包分解的PQD擾動識別算法步驟為:首先對PQD信號進行三層SVD包分解,再對分解后的子信號進行特征提取并作為分類器的輸入,選取隨機森林模型作為分類器,進行PQD問題的分類識別。

2.1 信號特征值提取

在信號分類過程中,輸入分類器的特征值提取數量越多,對各類擾動識別的精度也會更高,但特征值數量的增加會使算法計算負擔變重,經過對特征信號提取的最優化研究,本文對原始PQD信號經過三層SVD分解的8個子信號提取了包括信號均值、標準差、有效值、峰值因數、偏度、峭度等6個特征,特征值提取方法如下:

已知fi=[hi,1hi,2…hi,Z]為經過三層SVD包分解后產生位于第三層的八個分量信號,各特征值的提取方法為:

(1) 信號均值F1,fi,反映信號的平均波動幅值。

(10)

(2) 信號有效值F2,fi,反映信號的集中程度。

(11)

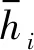
(12)

(4) 信號的峰值因數F4,fi,即信號峰值與有效值的倍數,式中rms(fi)為子信號的均方根,即信號的有效值,峰值因數可以反映信號的突變程度。

(13)

(5) 信號的偏度F5,fi,可以反映信號的不對稱程度。

(14)

(6) 信號的峭度F6,fi,是信號的四階矩平均,可以反映信號中的沖擊特征,式(13)與式(14)中的σ為信號的標準差。

(15)

2.2 隨機森林分類模型

隨機森林模型是一種以決策樹為基礎分類器的并行集成學習模型,通過Bootstep重采樣技術[11],解決了決策樹模型易發生過擬合的問題。隨機森林的預測結果由多顆決策樹各自獨立的投票結果決定,決策樹的組合使得數據集的并行訓練成為可能。通過少數服從多數的方式進行分類結果投票,使得隨機森林模型具備分類效果好、泛化能力強等特點。

隨機森林并不是使用所有的變量來分割樹節點,而是在每個節點處選擇變量的隨機子集來獲得節點的最佳分割。這樣隨機化的主要目的是去除相關的決策樹,使得所有樹的集合具有較低的方差。構造隨機森林的方法一般包括以下主要步驟[12]:

(1) 在原始數據中提取出n-tree個樣本子集。

(2) 利用每個樣本子集生成決策樹,在樹的每個節點,隨機選擇變量M進行分裂。繼續增長樹,使得每個終端節點的節點數不小于節點的大小。

(3) 采用投票機制統計n-tree個決策樹的結果進行分類。

隨機森林模型被普遍認為是具有高精度運算結果的分類模型,本文選取隨機森林模型作為分類器進行PQD問題分類,提出基于多分辨SVD包分解與隨機森林結合的PQD識別算法。

3 電能質量擾動識別實驗結果

本文以多分辨SVD為工具,在小波包分解的啟發下提出一種用于進行PQD問題分類辨識的MRSVD-RF算法,為了驗證算法的有效性,本節以多種PQD信號為對象進行仿真實驗。同時,為了驗證MRSVD信號分解方法較于小波包分解法在PQD問題分類上的優越性,本文還對基于小波包分解的特征提取與隨機森林結合(WP-RF)的算法進行了實驗,并通過對比體現了MRSVD-RF算法在分類精度等方面的優勢。

實驗所用的信號由MATLAB仿真軟件按照IEEE電能質量擾動標準[13]生成,信號類型共包含了正常波動的正弦信號、6種常見的單一擾動信號以及9種復合擾動信號,其中包括:d0(正常)、d1(暫降)、d2(暫升)、d3(中斷)、d4(諧波)、d5(脈沖)、d6(震蕩)、md1(暫降&中斷)、md2(暫降&諧波)、md3(暫降&震蕩)、md4(暫升&脈沖)、md5(暫升&震蕩)、md6(暫升&諧波)、md7(諧波&震蕩)、md8(暫降&脈沖)、md9(諧波&脈沖)。信號分別添加了不同程度的高斯白噪聲,部分復合擾動信號展示如圖4所示。

圖4 信噪比為30 dB的復合電能質量擾動信號展示圖

3.1 MRSVD-RF算法實驗結果

本文對包含了正常擾動、單一擾動和復合擾動的16類信號隨機各生產1 000條數據,選取其中800條為訓練數據,200條為測試數據進行PQD問題分類實驗,在實驗過程中依次添加了噪聲信噪比為30、40和50 dB的高斯白噪聲以測試算法在噪聲環境下的分類能力。實驗中先用本文1.2節闡述分解方法進行原始信號分解并選取第三層SVD分解后的8個子信號,對子信號提取2.1節闡述的6個F1～6特征向量,使一條PQD信號對應48個輸入特征,采用MRSVD-RF算法對每一類擾動的識別準確率分別進行分析,結果如表1所示。

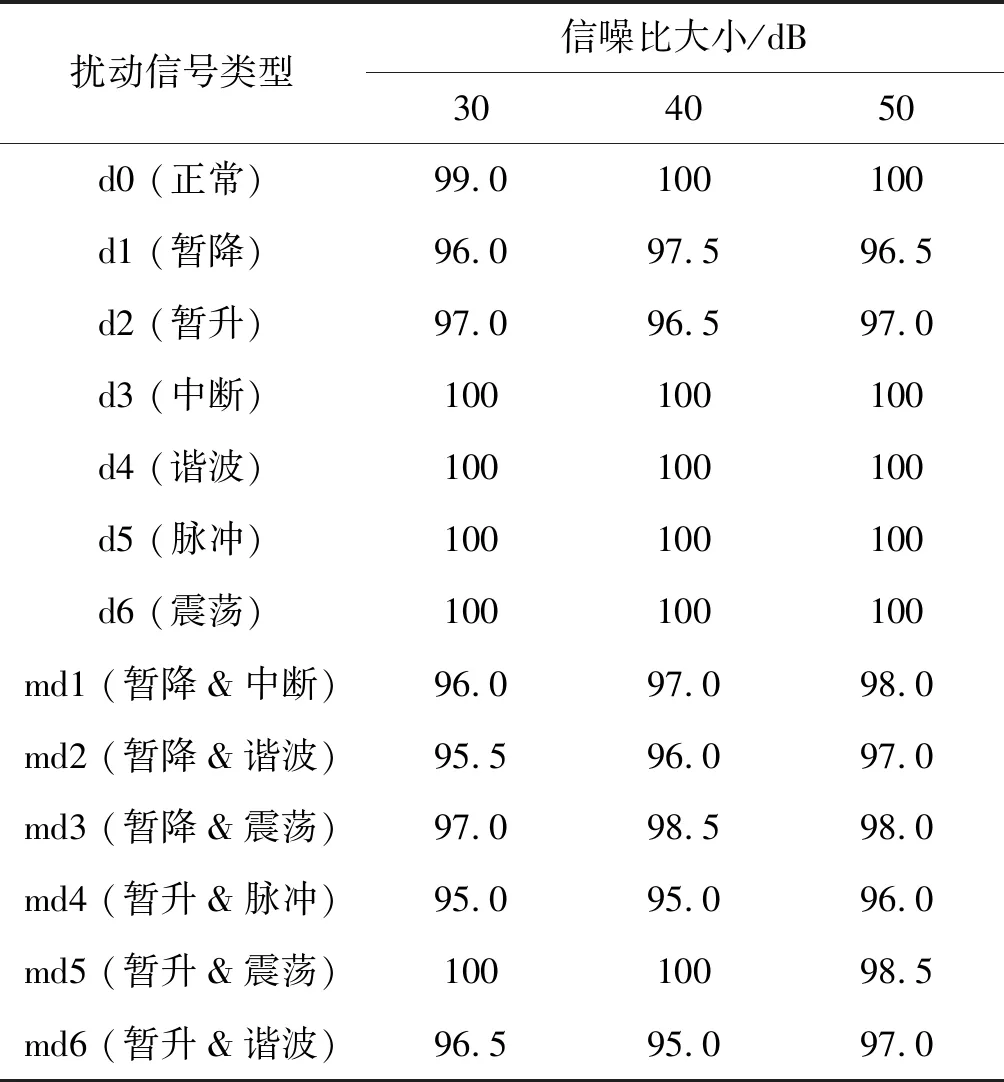
表1 MRSVD-RF算法對每類擾動的識別準確率(%)

如表1所示,本文提出的MRSVD-RF算法識別準確率隨著噪聲信號的增大而減小,同時對復合擾動的識別能力低于大部分單一擾動識別的準確率,主要的識別錯誤集中發生在暫降、暫升信號及其混合信號中,但均表現出了較好的識別能力。

3.2 MRSVD-RF算法與WP-RF算法的對比實驗

本文提出的MRSVD算法借鑒小波包分解的方式對原始信號進行分解并提取特征,因此有必要將本文算法和WP-RF算法進行結果對比,小波包分解過程和小波基選取參考文獻[14],WP-RF算法的特征向量求取方法和3.1節中MRSVD算法相同,在分解層數和提取特征子信號個數相同的情況下, MRSVD-RF算法與WP-RF算法對相同PQD信號的分類效果如表2所示。

表2 特征提取方式不同時算法識別準確率的效果對比(%)

表2中實驗結果是多次實驗結果取平均值得出的平均識別準確率。由實驗結果可知,在PQD問題分類研究中,MRSVD-RF算法識別效果較好,小波包分解的方式雖與SVD包相似,但在提取的特征量和分解的信號量都是一致的情況下,SVD包的分解效果要優于小波包的效果。可見,基于多分辨率SVD包分解的算法可以更好地獲取信號中擾動特征,較小波包分解可以更精細地挖掘信號的細節變化。

3.3 MRSVD算法使用不同分類器的對比實驗

為了驗證本文選擇的隨機森林分類器的優越性,將基于本文提出的MRSVD方法提取的PQD信號特征輸入極限學習機(Extreme Learning Machine, ELM)與K-近鄰(K-Nearest Neighbor,KNN),分別組成MRSVD-ELM算法和MRSVD-KNN算法進行分類識別。ELM是一種網絡學習算法,它在單隱層前饋網絡的隱層節點的激活函數無限可微時,隨機確定節點的偏置與輸入權值,并且可以快速得到輸出權值,因此該算法具有較好的學習速率,并且也避免了陷入局部最優的風險[15]。KNN是一種基于統計的分類算法,通過測量未知樣本的K個近鄰數,統計K個近鄰大多數屬于的類別,KNN的原理較簡單,在分類和模式識別方面有廣泛的運用[16]。對ELM和KNN的參數設置參照文獻[15-16],三種分類模型進行擾動識別的平均識別準確率如表3所示。

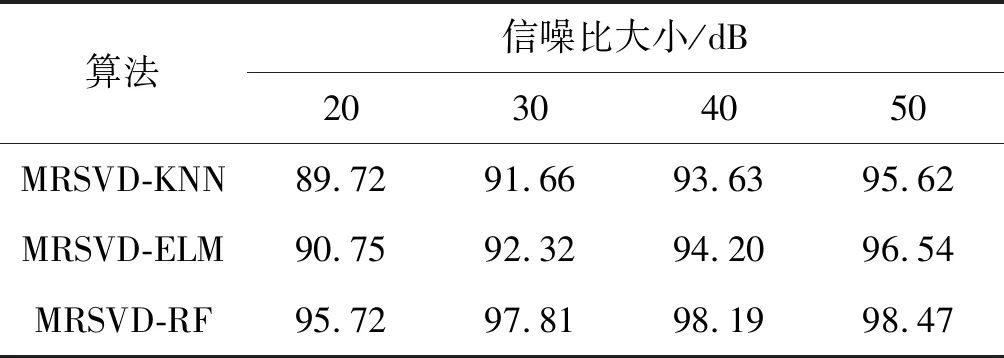
表3 分類器不同時算法識別準確率的效果對比(%)

由表3可知,在使用MRSVD算法進行分解后,使用不同的分類器對識別結果的影響較大,MRSVD-KNN算法的擾動識別結果與MRSVD-ELM算法相差不大,其中ELM的分類效果略好于KNN算法,但是對比RF分類器均有較大的分類精度差距,且ELM和KNN分類器的參數設置較RF分類器更為復雜,實驗表明,本文選取RF分類器的分類效果要明顯好于其他兩個分類器。

3.4 特征值選取的對比實驗

根據本文3.1節闡述的對輸入分類器的特征值求取方法可知,MRSVD-RF算法中用于分類的特征值數量,是信號分解后子信號數與針對每條子信號求取特征向量個數的乘積,分解后子信號的個數與使用MRSVD算法分解的層數相關,為了說明MRSVD-RF算法的性能與特征值數量的關系,本節分別通過減少分解后子信號個數和增加對子信號提取特征值的種類來實現特征值數量的減少和增多,分解子信號的減少通過降低MRSVD算法分解層數實現。

(1) 增加提取特征值的種類及數量。

在2.1節提取的6個特征值的基礎上,再增加兩個特征值:信號的能量F7,fi及信號的能量熵F8,fi。其計算方法分別如下:

(16)

(17)

在對信號進行了三層MRSVD分解后,對第三層8個分量信號分別提取不同的特征值,即一組提取6個F1～6特征向量,共48個輸入特征;另一組提取8個F1～8特征向量,共64個輸入特征。實驗結果如表4所示。

表4 特征值數量增加時識別準確率對比(%)

(2) 減少提取特征值的數量。

在保持2.1節介紹的提取的6個特征值不變的基礎上,減少MRSVD分解的層數,只對信號進行兩層分解,并提取第二層分解得到的四個分量信號進行特征提取,在不同噪聲環境下實驗結果如表5所示。

表5 特征值數量減少時識別準確率對比(%)

由表4和表5可知,MRSVD-RF算法的分類準確率和提取特征值數量是正向相關的,值得一提的是,僅依靠經過兩層SVD分解的4個子信號依然可以完成對PQD信號的有效分類識別,但隨著噪聲水平的升高,算法的準確率會大幅降低。通過定性的分析可以得出隨著SVD分解層數的增加,子信號對原始信號的反應更加全面。同時,隨著特征提取種類和數量的增加算法分類效果也得到優化,但這同時造成了更大的計算負擔。本文通過實驗法選取了8個分量求取6種特征值的組合,使得算法在盡可能小的計算負擔下完成精準的PQD擾動分類辨識,但是如何通過定量的分析,使算法在算法準確率與計算量之間達到平衡,仍需要進一步探究。

4 結 語

本文受小波包分解算法的啟示,為PQD問題識別研究提出了一種新的MRSVD-RF算法,以類似小波包分解的方式對信號進行MRSVD算法分解,并對分解后的分量信號進行特征提取,最后采用隨機森林模型對擾動進行分類。

本文通過實驗證明了MRSVD-RF算法的有效性,且其分類效果優于基于小波包分解的WP-RF算法,可以實現對單一和復合擾動的PQD信號分類,是一種有效的PQD分類算法。本文還對影響算法分類效果的分類器選取以及特征值數量進行了研究,通過控制變量實驗證明了本文選取分類器模型和特征值方法的優越性,但是還缺乏對特征值數量以及分解層數對算法性能影響的定量分析,后續的研究方向應在如何搭建模型進行分析,從而在算法的計算量和分解層數、特征值數量選取中尋找平衡點進行研究。