基于誤差修正的短期光伏功率預測

張弛,朱宗玖

(安徽理工大學電氣與信息工程學院,淮南 232001)

在電網系統的安全調用、使用規劃、穩定運行中,光伏功率預測起著至關重要的作用。一個良好的預測模型有助于維持電力系統安全可靠地運行,使能源更加合理有效地使用,提高經濟效益。根據以往研究統計,提高短期預測的準確性的方法有很多,例如人工智能法與統計學法。統計學方法的底層邏輯是數學模型,如多元線性回歸分析,該方法主要用在線性模型中,而對于隨機性較強的功率預測(具有較強的非線性特征),在該類型預測方面模型效果較差。常見的預測模型如神經網絡在對光伏發電功率進行預測時,由于部分環境因素對光伏功率的影響被忽略,從而導致信息的有效利用率不足。近年,人工智能技術廣泛用于各個工業領域,光伏功率預測也逐漸向著具有不同結構的深度學習方向發展,而高精度預測的一個重要問題是由于負荷數據的復雜性和時序性導致特征不易抓取。隨著深度學習的發展,深度神經網絡等結構逐漸應用到復合預測領域如短期負荷預測問題中,功率預測精度上雖有所提升,但由于功率數據具有時序特征,往往容易被忽略。循環神經網絡(recurrent neural network,RNN)可解決上述時序問題,RNN引入循環結構對時間序列數據進行擬合,但是存在梯度消失的問題。長短期記憶(long-term and short-term memory,LSTM)網絡通過加入內存單元可解決梯度消失的問題,對于數據序列中的規律走向有著更完整的學習能力,通過歷史功率數據的分析可擁有更高的長時間預測精度。文獻[1]基于環境因素和歷史數據,提出一種復合結構網絡,采用主成分分析、經驗模態分解和長短期記憶神經網絡對光伏功率預測;文獻[2]提出一種極限學習機和修正互補經驗模態分解的風速預測模型;文獻[3]提出一種完備集成經驗模態分解(complementary ensemble empirical mode decomposition with adaptive noise,CEEMEDAN)并與結合自適應白噪聲相結合,最小二乘支持向量機(least squares support vector machines,LSSVM)和差分自回歸移動平均模型(autoregressive integrated moving average,ARIMA)的短期光伏功率預測方法。

基于以上研究,現提出一種基于ARIMA與改進結合自適應白噪聲完備集成經驗模態分解(improved complementary ensemble empirical mode decomposition with adaptive noise,ICEEMEDAN)的LSTM神經網絡光伏功率預測模型。首先對光伏數據集做預處理使之成為可直接進行實驗的數據序列。利用LSTM建立初級預測模型,導入經預處理后的光伏電站監測數據,其次結合歷史數據建立ICEEMEDAN-ARIMA殘差預測模型,該模型用于對初步預測結果的修正,最終實現對光伏功率進一步預測。將經實驗結果對比,復合模型有效地提高了光伏發電功率的預測精度。與傳統反向(back propagation)BP神經網絡及單一LSTM,EMD-LSTM等機器學習模型對比,提出的模型預測精度更高。

1 光伏功率影響因素分析

1.1 原理介紹

光伏功率預測,按照時間尺度范圍的分類可以分為如表1所示的三大類[4]。按方法分類大致可分為基于歷史實測數據的統計方法、基于站點周邊環境因素等的物理方法、數值天氣預報方法(numerical weather prediction,NWP)和機器學習或深度學習方法[5]。主流方法是基于NWP的光伏發電功率預測,由于準確的數值天氣預報很難獲得,因此目前在光伏發電功率預測的問題上,統計方法的應用更為廣泛。

表1 光伏功率預測時常與精度

光伏功率具有隨機性和波動性,這是由于光照和云層生消所決定的自然屬性。容量較小的電站并網對電網的影響較小,隨著光伏滲透率的增大,光伏集群功率的波動性對電網的安全運行存在不可忽略的影響,但隨著光伏集群容量的逐漸增大所帶來的影響并不會成比例增加。研究表明,隨著光伏集群總容量的提升,不同位置光伏電站的出力波動程度存在一定的抵消[6]。即光伏集群的輸出總功率存在波動性并在日周期內會逐漸降低,該現象稱為“匯聚效應”,主要原因在于光伏集群占地面積廣闊,不同地理區域光伏電站所接受的輻照度及云層遮擋存在空間上的差異。

1.2 影響因素

光照強度是光伏發電系統實時輸出功率的決定性因素[7]。忽略其他因素對功率的影響,光伏功率與輻照度的數學模型表達式為

(1)

式(1)中:Pb為光伏電站的實測功率,MW;Psn為該光伏電站的整場裝機容量,MW;Gstd為額定輻照度,W/m2;Rc為臨界輻照度,在超過該輻照強度后光伏出力與輻照度的關系變為線性;Gbt為第t小時實測輻照度,W/m2,Gbt對應功率序列由對歷史輻照強度的概率分布抽樣獲得[8]。

本次數據采取澳大利亞(DKASC)光伏發電站集群中2016年的實時監測數據進行分析,監測變量包括風速、攝氏溫度、輻照度、最大風速等七組不同數據,該光伏電站輸出功率的采樣間隔為5 min,每日采集的數據規模為7×298(輸入矩陣的橫縱軸)。

圖1所示為實測數據輻照度與功率的散點圖,通過計算該光伏電站2016年全年實測輻照度與功率散點圖以及散點擬合曲線,尤拉(Yulara Solar Systom)電站組的功率與輻照度相關系數[采用概率統計中的線性相關系數r(X,Y)來表示]為0.821 4,斯普林斯(Alice Springs)電站組的功率與輻照度相關系數為0.998 2,由此可以得出輻照度與功率整體呈正相關。

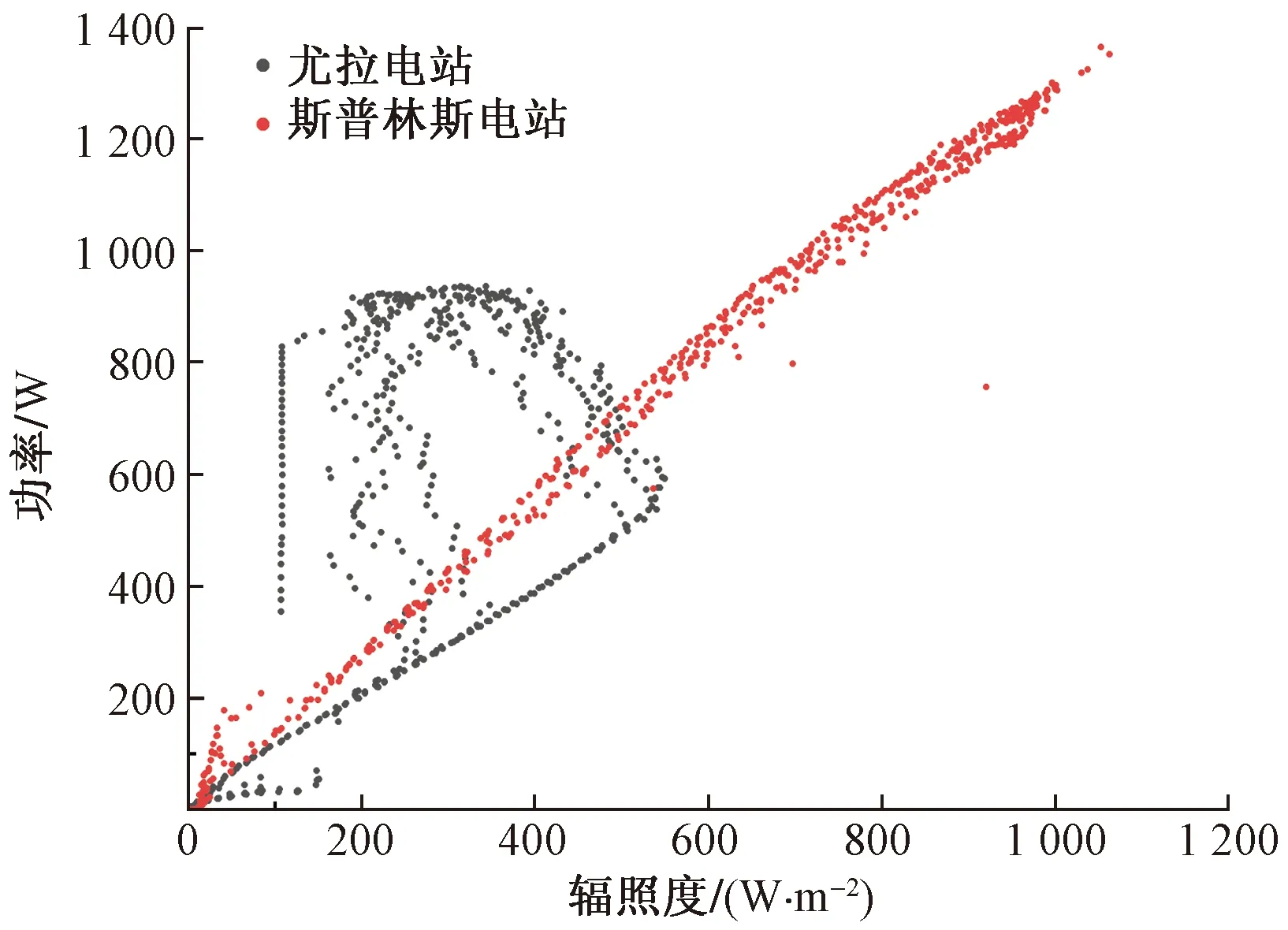
圖1 光伏功率與輻照度關系

2 基于LSTM的光伏功率預測模型

2.1 模型概述

長短期記憶神經網絡是一種具有記憶和篩選功能的網絡結構,如圖2所示LSTM中的單個細胞模塊包含一個雙曲正切結構(hyperbolic tangent),三個Sigmoid和四個交互的層[9],相比于RNN,LSTM的交互方式非常特殊。

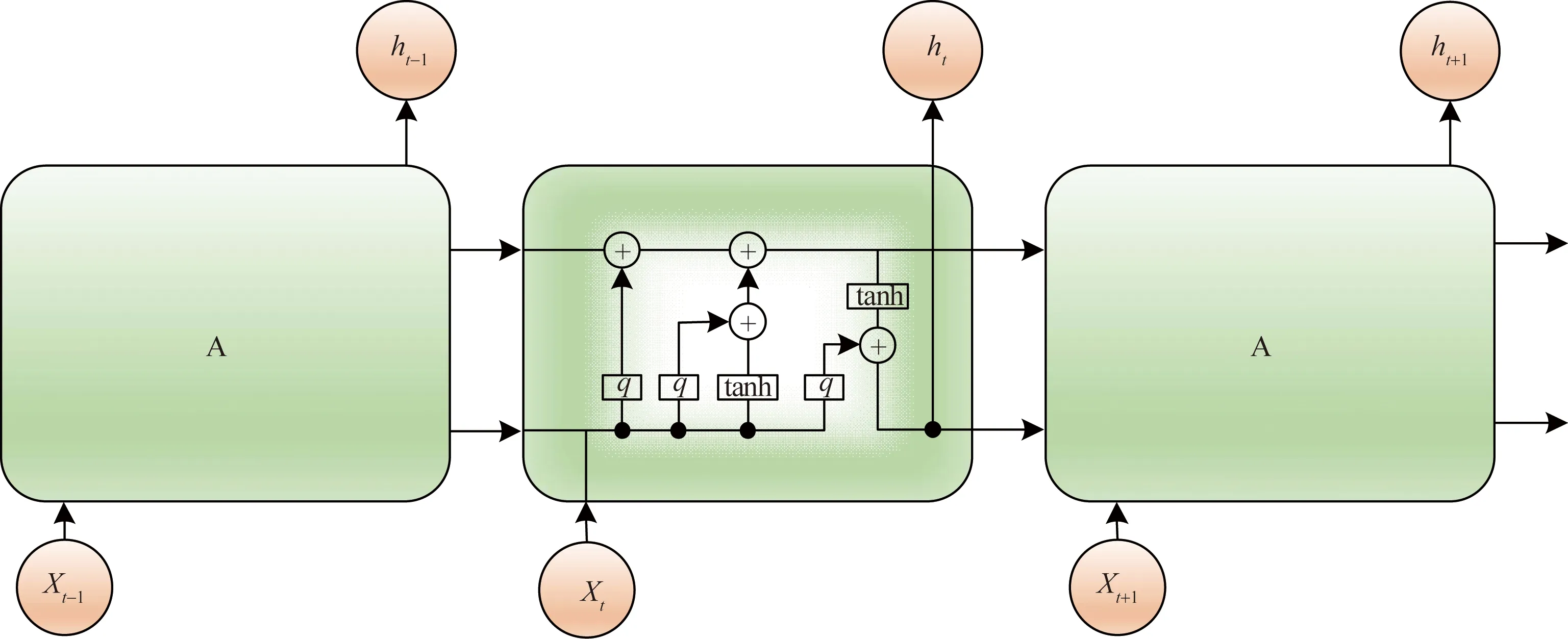
圖2 LSTM細胞結構

首先,“忘記門”的結構中會生成需要丟棄的部分細胞狀態的信息[10],通過讀取輸入(本單元)和輸出(上一個單元),“忘記門”做一個Sigmoid映射獲取一個輸出向量(越重要的越會記住,越無關緊要的越會舍棄),最終與細胞當前的狀態相乘。

ft=σ(Wf[ht-1,x]+bf)

(2)

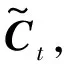
it=σ(Wi[ht-1,xt]+bi)

(3)

(4)

2.2 CEEMDAN-ARIMA

經驗模態分解(empirical mode decompsition,EMD)是一種針對信號進行變換的方法,在處理非線性不平穩信號的問題上尤為突出,其本質是希爾伯特-黃變換(Hilbert-Huang transform,HHT)的一部分。首先將原始信號分解為一系列本征核函數(intrinsic mode function,IMF),IMF分量是一種具有信號的局部特征的時變頻率的單分量信號,可以將原始信號的分量從高頻到低頻按不同時間尺度依次提取。

EMD是一種自適應時頻分析方法,容易出現模分量混合問題。集合經驗模態分解(ensemble empirical mode decompsition,EEMD)解決了這個問題,然而,EEMD帶來了較高的計算成本,并且重建的信號包含殘余噪聲。為了解決這些限制,開發了互補集成經驗模態分解(complementary ensemble empirical mode decomposition,CEEMD)。EEMD和CEEMD 都傾向于產生不正確的組件。完全自適應噪聲集合經驗模態分解(complementary ensemble empirical mode decompsition,CEEMDAN)解決了這些題,但完全自適應噪聲集合經驗模態分解仍然存在一些問題。由此,ICEEMDAN方法被提出[11],在后處理過程中,應用ICEEMDAN將殘差序列分解為若干個子序列,便于預測誤差序列。

差分自回歸移動平均(ARIMA)模型[12]是常用的時間序列預測模型。通過ARIMA來實現非平穩時序的轉化,其過程可高效地將非穩定數據轉換為穩定數據。ARIMA模型已廣泛用于各種時間序列預測應用,因為它穩健,便于理解和易于實施。

2.3 評價標準

實驗中使用均方根誤差(root mean square error,RMSE)、均方誤差(mean square error,MSE)和R2[13]來作為評價模型性能好壞的標準,其相應表達式如下。

均方誤差[14]是預測值與真實值偏差的平方和的平均數。均方誤差的數學表達式為

(5)

均方根誤差即真實值與預測值之間偏差的平方和與時序次數比值的平方根。其數學表達式為

(6)

R2的取值范圍為[0,1],如果是負數,則考慮非線性相關[15],結果越趨近于0時,模型擬合效果越差,結果為1時,模型擬合效果最好。通常R2越大,代表模型擬合越趨于完美。R2的數學表達式為

(7)

3 建模過程

模型的搭建首先是單一模型LSTM的使用,由于單一模型對數據只做預處理和一次處理,精度無法得到進一步提升,所以這里需要采用二次處理即后續的誤差修正模型對模型整體性能進行優化[16]。詳細建模步驟如下。

(1)將采集數據作為特征輸入到LSTM模型中,對數據進行預處理,空缺數據和異常數據用上一單元數據填補,并對數據進行歸一化處理[17]。首先利用LSTM模型通過特征輸入進行初步預測,該步驟完成后輸出即為預測量,通過預測量與真實量的值獲取殘差值并輸出到下一模型。

(2)利用ICEEMDAN對殘差序列進行分解,獲取不同頻段的IMF,再用ARIMA對分解后的各殘差序列進行預測,模型結構如圖3所示。

(3)殘差序列被ICEEMDAN分解為若干個子序列后,利用ARIMA模型對每個誤差子序列進行預測。圖3所示為ARIMA模型獲得的每個誤差子序列的超前一步預測結果。然后將各個子序列的預測值聚合,得到殘差的預測值。

(4)將殘差預測值與(1)中獲得的LSTM預測值得到的預測值相加,得到最終的功率預測結果。

4 模型結果分析

4.1 敏感性分析

算例部分采用的數據為日期為DKASC 2016年的光伏數據集,分別從Yulara Solar Systom光伏電站與Alice Springs光伏電站中各選取一組數據,單組數據共含有12 d的數據量共3 456組。訓練集與測試集按75%與25%的比例劃分[18],分配完成并調整模型的基礎參數,將訓練集與測試集輸入LSTM模型之中進行訓練,訓練完成的LSTM模型與ICEEMEDAN-ARIMA模型協同作用輸出最終預測結果。

針對不同的天氣變量,包括太陽角度和地外輻照度進行神經網絡預測實驗,以確定哪些是預測光伏發電功率的良好預測因子[19]。結果如圖4所示,分別為去除表2中A～G六組變量后的模型以及H組中包含全部變量的模型誤差對照(對照標準為MAE)。通常水平面總輻照度(global horizontal irradiation,GHI)是光伏功率模型預測變量出力的主要因素,如果不將GHI作為輸入,模型的準確性會大大下降,當排除日照時,圖4中的MAE會增加。標記(輸入集中不包括陽光)的MAE框的四分位距相較于其余框比較大,標記(輸入集中不包括陽光)的MAE框的中值大于其余箱形圖的中值。

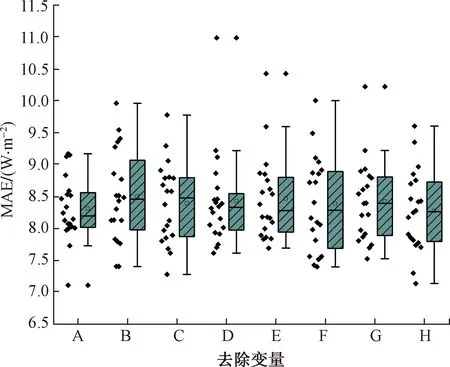
圖4 LSTM模型對不同天氣變量敏感性

表2 不同組去除變量的編號

如圖4所示,當變量A、B、C、F去除之后,MAE的中值相較于其他組明顯較低,這表明風速、攝氏溫度、水平面總輻照度、最大風速是預測光伏功率的重要天氣變量。如果將所有天氣變量都包括在內(表2中的編號H)作為輸入,則光伏功率神經網絡預測誤差的中值減小,MAE的最大值、上四分位值、中值、下四分位值也會有所減小(圖4)。

通過損失函數來估量在模型訓練中預測值與真實值的偏差程度[20],它的值為正且總在0～1,通常使用L[Y,f(x)]來表示,損失函數的大小決定模型魯棒性的優劣。圖5為Yulara Solar Systom和Alice Springs兩個光伏電站光伏功率預測模型的損失函數。可以看出,在訓練次數小于10的范圍,模型損失率會隨次數增加而快速下降,當訓練次數大于10則逐漸趨于穩定。

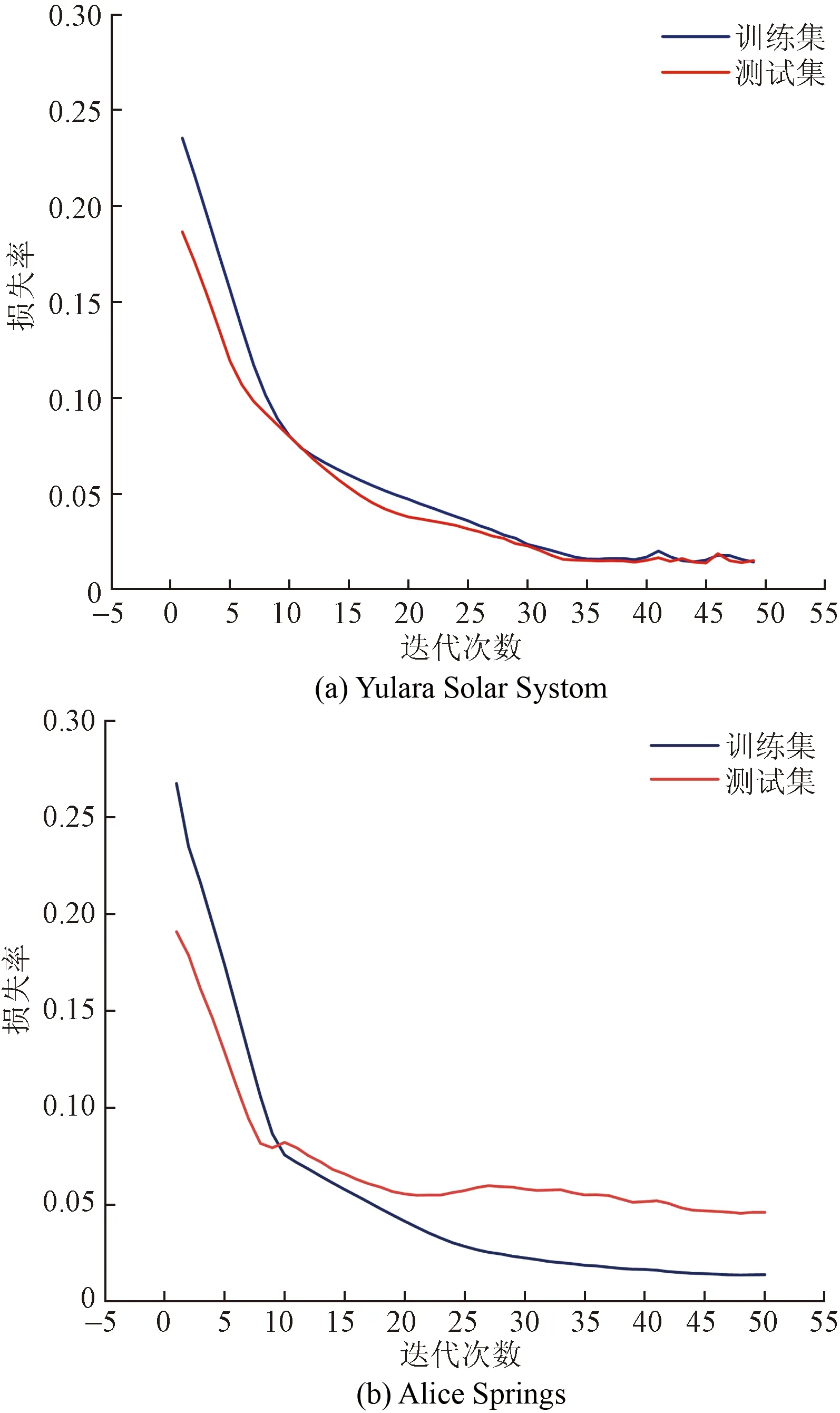
圖5 電站訓練集與測試集損失函數

4.2 測量結果分析

通過時序數據獲得定量的本征模函數(本次實驗中本征模函數的個數為7,橫坐標刻度為時間序列)[21]。首先利用ICEEMDAN模型對原始功率殘差進行分解,該方法可以解決CEEMDAN中殘留噪聲和偽模態的問題。將原始殘差分解為IMF1～MF7七個不同頻段,每個頻段都包含時變頻率信息。分解結果如圖6所示,可以看出,波形的頻率特征(波形密集度)主要成分集中在前三個本征模函數中,且范圍較窄,這也是時序數據中最重要的組成部分,能夠反映時序數據的主要特征。尾部分量IMF7是分解后的殘余分量,幾乎不包含原始時序信號的頻段特征,主要作用提供數值累加。

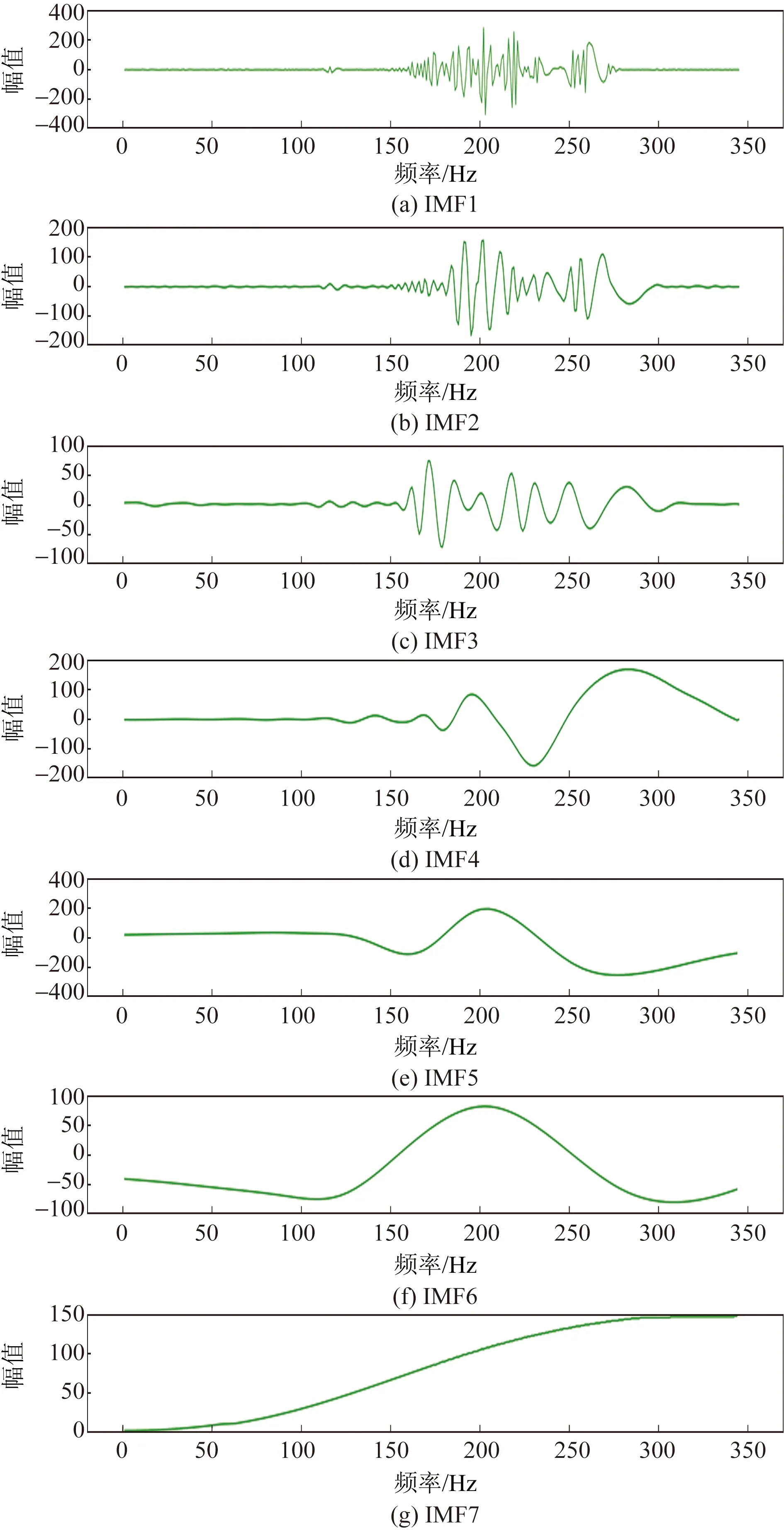
圖6 Yulara Solar Systom電站功率殘差分解結果

下一步利用ARIMA模型對各功率的子信號進行預測。這里的基本算法是以ICEEMDAN-ARIMA模型的框架,搭建出殘差預測模型。

該模型的步驟為如下。

利用ARIMA模型對分解后的IMF部分進行預測,該步驟最終得到預測結果的線性部分,數據序列的非線性Rn序列由預測結果與原始數據進行求差得到,將所獲取的殘差序列重新排序得到ICEEMDAN模型的新樣本序列,利用ARIMA模型對各部分樣本序列做出預測得到預測結果,最后將兩部分預測結果即線性部分與Rn進行加和,得到最終的組合殘差預測結果。

圖7所示為部分殘差預測預測結果(IMF1～IMF7)與原始數據的重合度,可以看出,從1到7,隨著分解度的提高,預測精度會有明顯地提升。

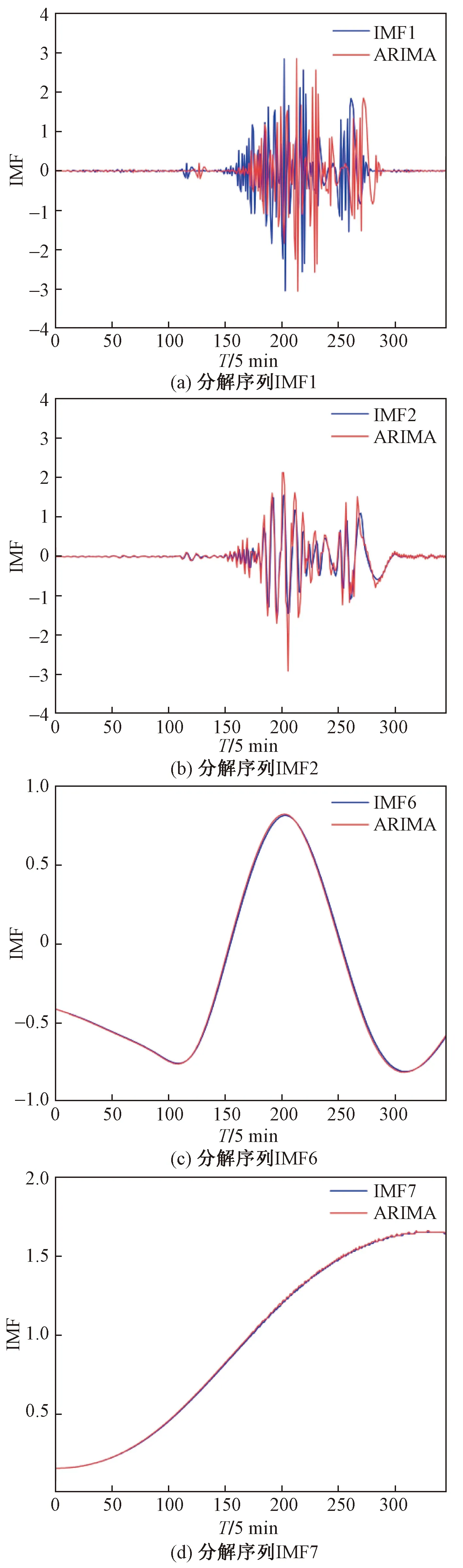
圖7 ARIMA模型下Alice Springs電站殘差序列預測值

然后將各個分解序列的ARIMA模型預測值進行合并,獲得最終殘差序列的預測值。如圖8展示了殘差序列真實值和預測值。

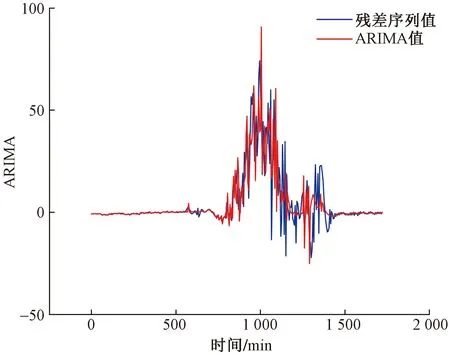
圖8 Alice Springs電站不同模型預測值與真實值對比

圖9為Alice Springs與Yulara Solar Systom電站在兩個不同模型中的測量結果的統計圖。對比模型有兩個,第一部分包括LSTM,它們是單一模型。第二部分是修正后的模型LSTM-ICEEMDAN-ARIMA,單一模型和混合模型之間的性能比較如下所示,可以看出LSTM模型對原始數據的規律捕捉和刻畫能力較差,功率值在同一時序下的變化規律與基于ICEEMEDAN-ARIMA的LSTM組合模型的預測結果較為相似,修正模型LSTM-ICEEMDAN-ARIMA相較于單一模型LSTM要更貼近真實值,修正模型整體的平均R2在數值上更高,為96.35%,而單一模型的平均R2為94.11%。因此,修正預測模型的整體預測精度更高。

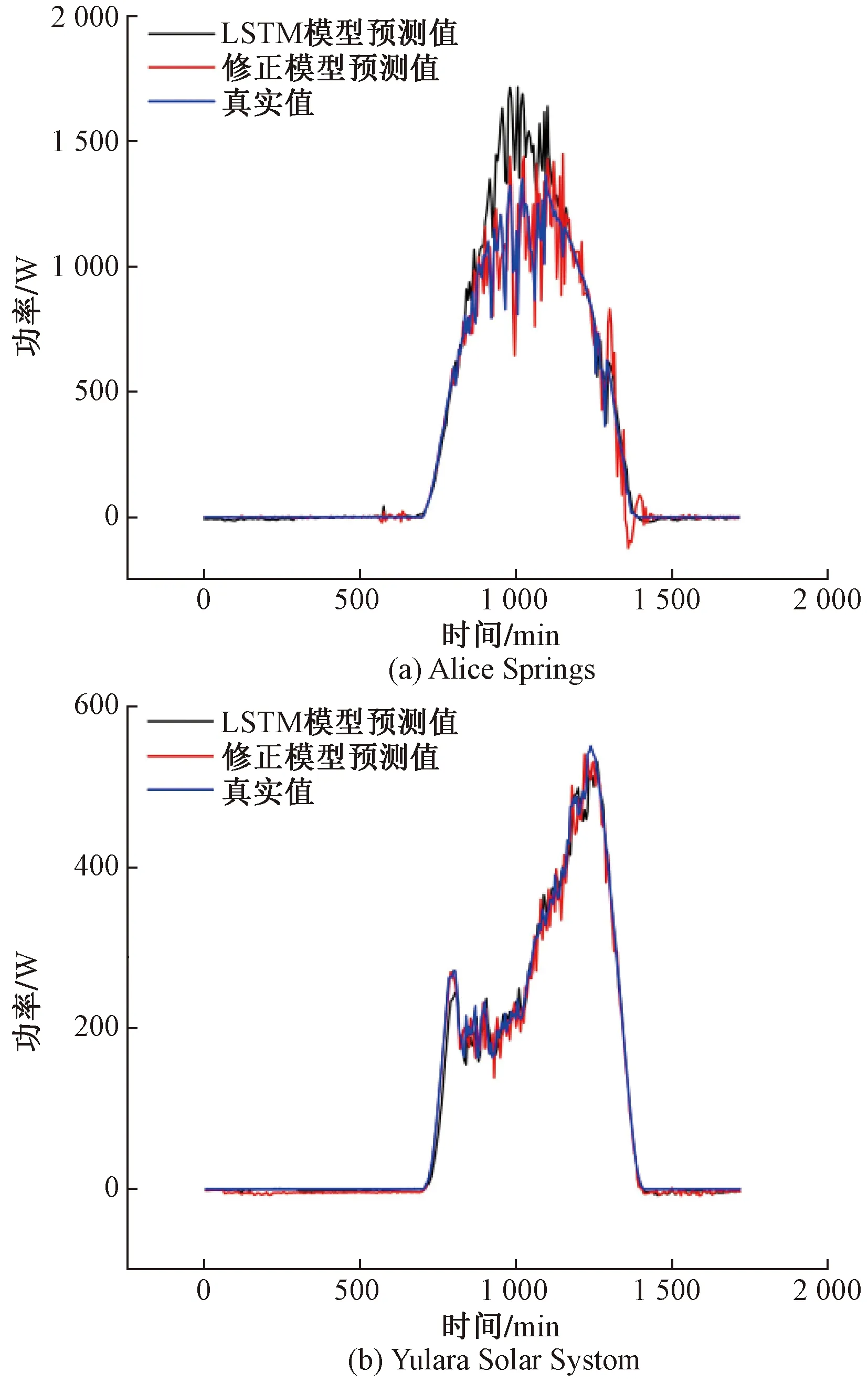
圖9 Alice Springs與Yulara Solar Systom電站不同模型預測值與真實值對比

表3展示了對于Alice Springs和Yulara Solar Systom兩個不同的發電站預測數據的評估值(每組重復測量三次),由圖9、表3分析可知,對比RMSE和R2值,合成模型LSTM-ICEEMDAN-ARIMA的準確度相較于單一模型LSTM有一定的提高,誤差上則有所降低,符合實驗預期。對于Alice Springs電站與Yulara Solar Systom電站的功率預測實驗,混合預測模型的MSE與單一的LSTM模型相比,分別降低了52.2%～61.22%,5.2%～24.79%,RMSE分別降低了30.86%～37.72%,4.78%～13.23%。R2則分別提高了2.15%～3.27%,0～0.07%。

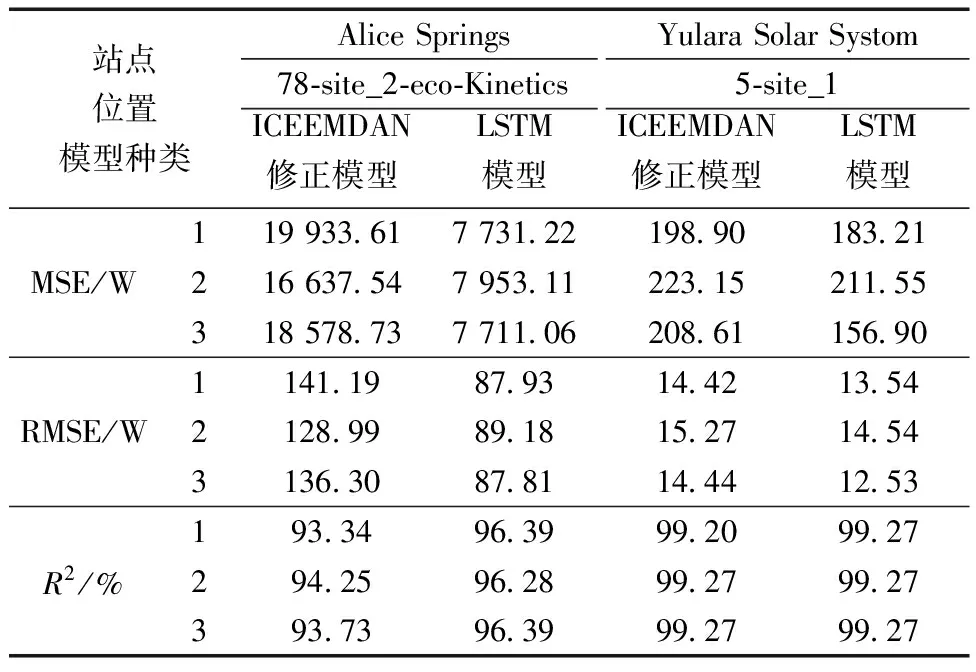
表3 不同評價指標模型準確率對比

LSTM神經網絡模型與LSTM-ICEEMDAN-ARIMA模型的預測誤差對照表如表3所示,分別為MSE、RMSE、R2三組測量誤差對比,每組測量三次。

5 結論

本文分析了各種影響因素下不同光伏集群功率短期預測模型的性質,針對光伏功率輸出值波動性較大及隨機性較強的問題,提出了一種基于LSTM-ICEEMDAN-ARIMA神經網絡的光伏電站發電功率的混合預測模型,ICEEMDAN模型的加入使光伏功率中具有較大波動性的序列得以準確預測,該方法中的ARIMA也可以直接作為預測光伏功率的預處理模型。實驗中主要考慮風速、天氣溫度、全球水平輻射、風向、降雨量、最大風速、空氣壓力7組變量,本研究進行了兩組對比實驗,算例分析得到以下結論。

(1)采用ICEEMDAN對光伏變量進行分解,對不同本征模分量及殘差項進行預測,可降低光伏序列隨機性對預測結果的干擾。

(2) 利用LSTM神經網絡和ICEEMDAN-ARIMA模型對多變量時間序列與光伏功率序列之間的非線性關系進行動態時間建模,構建混合預測模型,包括預處理和后處理模型,該模型比單一模型具有更高的預測精度。

(3)后處理模型比單獨的LSTM具有更高的預測精度。特別是,LSTM-ICEEMDAN-ARIMA模型在兩個研究地點將RMSE誤差值分別降低了37.72%和13.23%,R2則分別提高了3.27%,0.07%。

本文測試了LSTM模型及其復合模型在光伏預測領域的實用性,提出的預測模型在光伏并網系統及光伏能源的運輸調度中具有一定意義,在實際工程中擁有良好的前景與應用價值。