直線型柱塞式平衡調節閥結構優化研究

于正昌，郭健翔，2，張龍，孫晉飛，2，劉占杰

(1.青島理工大學環境與市政工程學院，山東青島266525；2.山東省余熱利用及節能裝備重點實驗室，山東青島266525)

0 前言

靜態水力失調是一種發生在空調和采暖系統中固有的水力失調，通常通過設置靜態平衡閥達到平衡各個環路的目的[1]。靜態平衡閥需要明確流量-壓差-開度對應關系即Kv曲線，實現只測量閥門兩端壓差便能計算出某一開度下的流量的目的[2]。常見的閥門流量特征有4種[3]，分別是直線型、等百分比型、快開型以及拋物線型。相比較來說，直線型流量特征更直觀地表現了Kv值與開度的對應關系，并可以通過線性擬合得出較準確的函數關系，更加適合作為靜態平衡閥的流量特征。

隨著調節閥種類越來越多，經驗公式已經無法適用于所有新型閥門的設計，需要進行大量試驗對閥門結構逐漸調整，且每次調整結構都需要重新制作樣閥，耗費了大量社會資源。計算流體力學應運而出，在閥門研發上的應用越來越廣泛。眾多學者針對不同結構的調節閥，就閥內的流動情況、空化氣蝕現象以及調節閥的流量特性都進行了大量研究。徐宏海等[4]對內部復雜的調節閥流場進行了三維模擬，通過比較調節閥的理論流量系數和模擬計算值，發現兩者吻合良好、誤差較小，驗證了將CFD技術應用于調節閥流場的可行性并為其他閥門的模擬提供了參考。趙瑩[5]以液體火箭發動機用球閥為例，模擬定流量和變流量條件下的流場，得到了流量系數與球閥開度的對應關系，并輔以相關實驗進行驗證，發現仿真結果與實驗結果高度一致。由于仿真模擬結果的可視化，眾多學者借助CFD技術觀察到調節閥內部不穩定因素，并依據相關經驗對閥門結構進行優化，以降低甚至消除不利因素的影響。吳佳寶[6]以軸流式止回閥作為研究對象，通過對閥芯以及流道型線的分析和優化，消除了閥門中回流、速度分布不均以及流體擁塞等現象，并配合流阻系數試驗驗證了模擬的準確性。為了使壓力調節閥安全可靠地應用在輸油管線中，魏丹[7]借助仿真模擬軟件Fluent找出閥門現有的不足，進而對齒形串級結構以及二級節流孔形狀進行一定優化，并與優化前對比發現，優化后的閥門內部流動更加穩定。

本文作者以數值模擬為主、實驗測試為輔驗證模擬方案的正確性，從而保證優化平衡閥結構的可靠性。

1 調節閥原始結構建模仿真

1.1 物理模型建立

對DA-J80-40-00靜態平衡閥進行物理建模，總體結構如圖1所示。該柱塞式調節閥由閥體、閥蓋、手輪、閥桿、閥瓣、閥芯、緊鎖桿以及相關密封圈組成。該閥門調節原理為：旋轉閥門手輪，閥桿隨之轉動，帶動閥瓣升降，達到調節閥芯與閥座距離的目的，實現開度調節。閥門開度改變，流體流經閥門的阻力也隨之改變，達到調節流量的目的。

圖1 調節閥三維結構剖面圖

為保證調節閥內部流動模擬結果的準確性，按照閥門測試的標準進行管道設置[8]，在閥門進口端添加一段5D的直管段，在閥門出口添加一段10D的直管段。總體結構如圖2所示，流道模型如圖3所示。在計算閥門兩端壓降時，采用公式(1)：

Δpv=Δp1-Δp2

(1)

式中：Δpv代表流體流經閥門兩端的壓降；Δp1代表流體流經整個系統的壓降；Δp2代表流體流經進出口總長度直管段的壓降(單獨進行模擬計算)。

圖2 直管段-調節閥總體結構

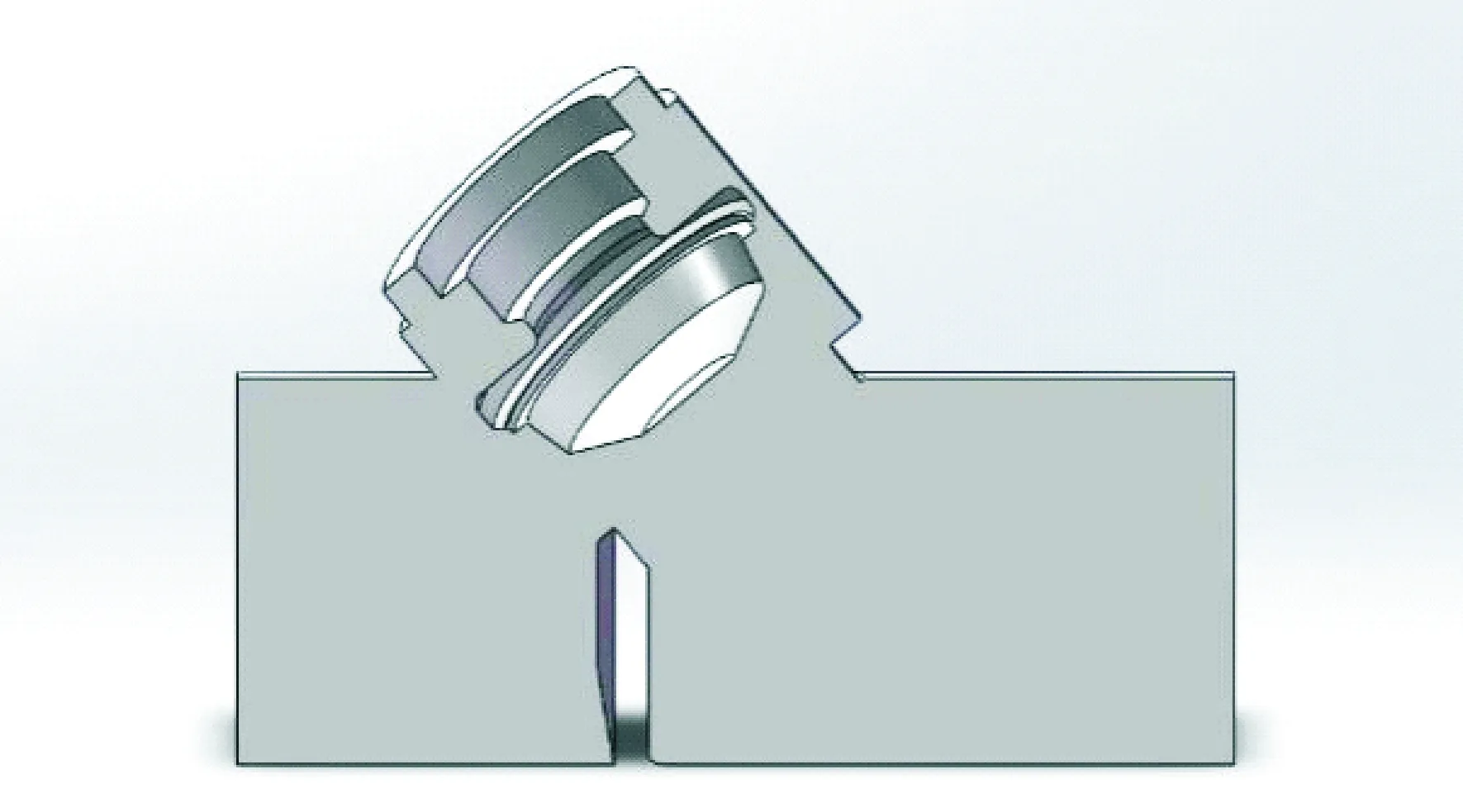
圖3 調節閥全開時流道模型

1.2 網格無關性驗證

以調節閥全開狀態的流道為例作網格無關性驗證，分別劃分5.4×105、7.4×105、9.4×105以及1.09×106這4種不同數量網格，網格質量均穩定在0.4以上、網格傾斜度均在0.84以下。設置的邊界條件均是2 m/s的速度進口以及101.3 kPa的壓力出口，以該速度進口條件下的質量流量M=3.175 1 kg/s為標準值，獲得網格無關性檢驗結果如表1所示。隨著網格數量增大到7.4×105，模擬結果就已經相差不大了，綜合考慮7.4×105為適宜的網格數量。

表1 網格無關性驗證

1.3 求解與邊界條件設置

文中選用定流量以及定壓降2種工況，取2種工況下的平均值作為模擬值，2種工況邊界條件設置如表2所示。在流動過程中，流體會在閥芯處產生繞流，故采用Realizableκ-ε紊流模型[9]；壓力速度耦合算法采用 SIMPLE 算法，壓力插值方式采用二階插值方式，單元中心的變量梯度選擇Least Squares Cell Based，其他項采用二階迎風插值，計算至收斂。

表2 邊界條件設置

1.4 結果分析

通過對模擬數據的整理，按照公式(2)，計算得出閥門每個開度下的Kv值，并繪制Kv曲線觀察分析該閥門的流量特性。相關數據記錄見表3、4。

(2)

式中：Q為某一開度下的閥門流量，m3/h；ρ0為水在15 ℃下的密度，一般情況下認為ρ0/ρ=1；Δpv為某一開度下閥門兩端的壓差，kPa。

由表3、4可以看出：隨著閥門開度增大，在定流量工況時，流體通過閥門的壓降變小；在定壓降工況時，流體通過閥門的流量增大，可見隨著閥門開度增大，閥門流通能力變好。

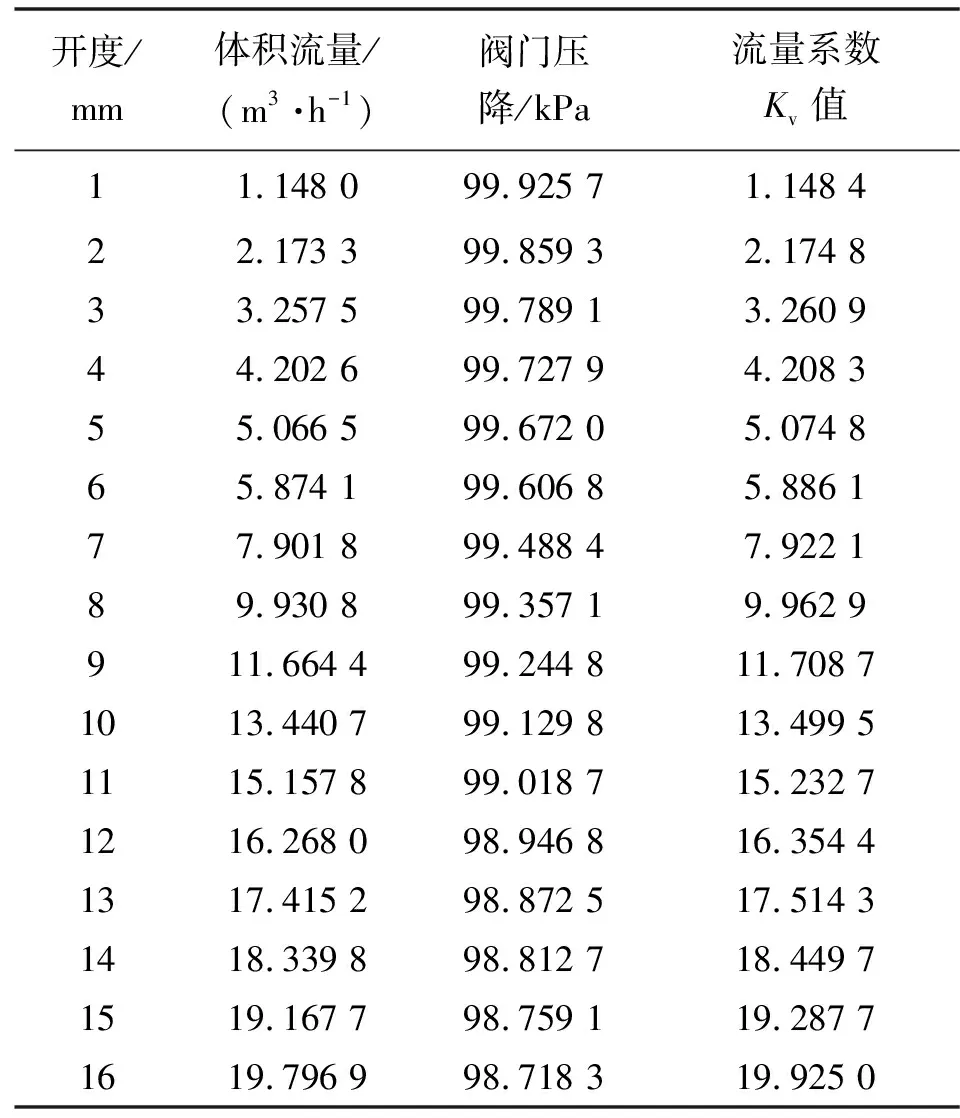
表3 流量系數(定壓降工況)

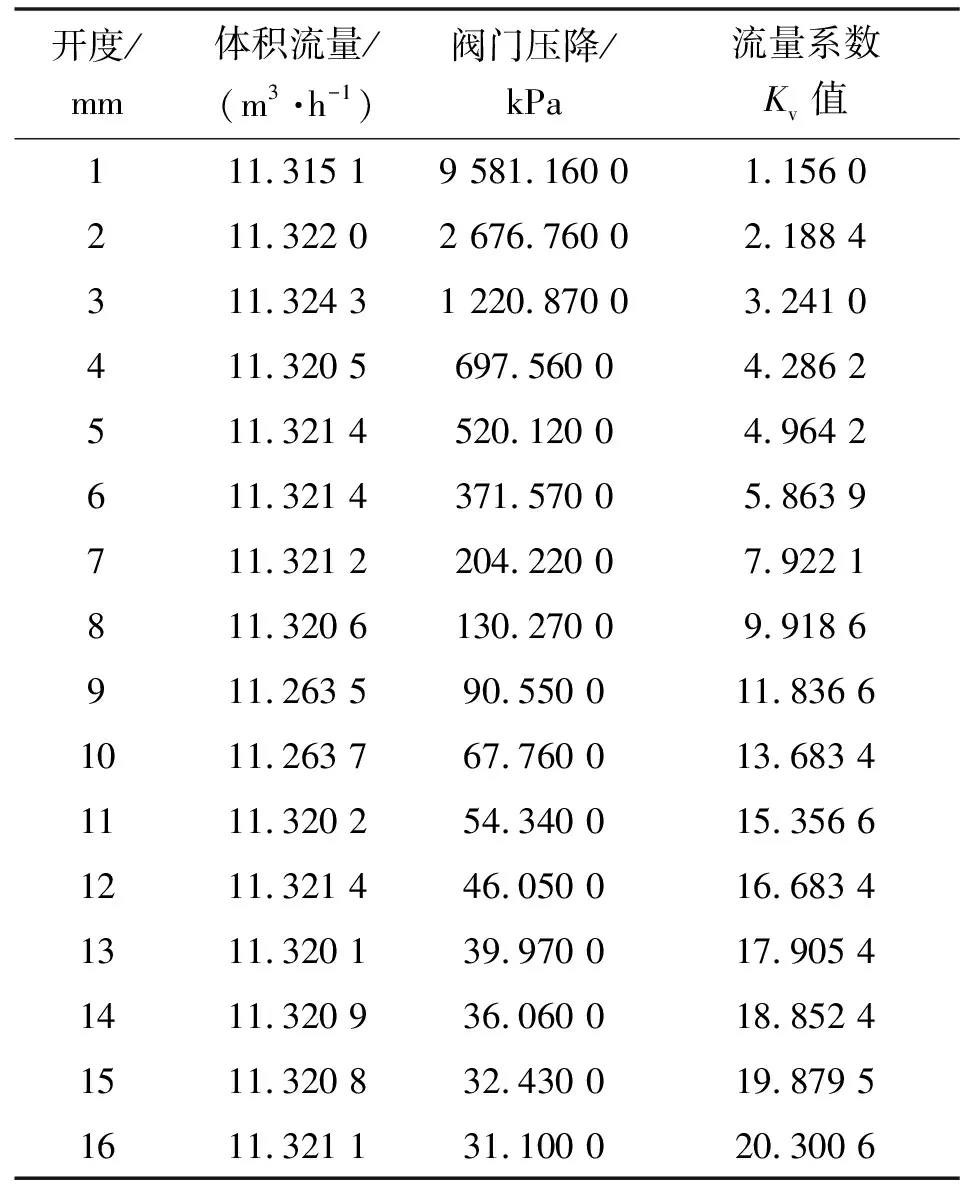
表4 流量系數(定流量工況)

2 可行性分析

2.1 實驗測試

數值模擬可以清晰地觀察到調節閥內的復雜流動，但是在數值模擬復雜流動的過程中，采用的數學模型以及仿真方案可能會與實際情況有所偏差。因此對調節閥進行一定的實驗不僅可以檢測調節閥實際情況，同時也能對數值模擬的準確性進行驗證。實驗裝置如圖4所示。

試驗過程中，固定試驗閥門的開度，調節下游閥門的開度，使試驗流量在容許范圍內，并在10 s后觀測流量計。試驗所用的電磁流量計和壓力傳感器的精度均在規定范圍內。在確定流量時，最大值與極小值之差不應超過偏離平均值的1.2%。為了使測試結果盡可能準確，要在流量和壓差穩定的情況下讀寫測試數據。特定的操作是每個流程都有5 s以上的時間間隔，同時記錄流程和壓差。該被測閥門為手動調節閥，閥芯行程為16 mm，手輪可以旋轉4圈，故選擇8個開度進行測試，記錄調節閥在不同開度下的流量和閥門兩端的壓力差，相同開度下記錄4次測試數據，整理數據如表5所示。

2.2 可行性分析

通過試驗測試得到了閥門部分開度的Kv值，將它與同樣開度下的模擬數據進行對比驗證數值模擬的可行性，相關數據如表6所示。

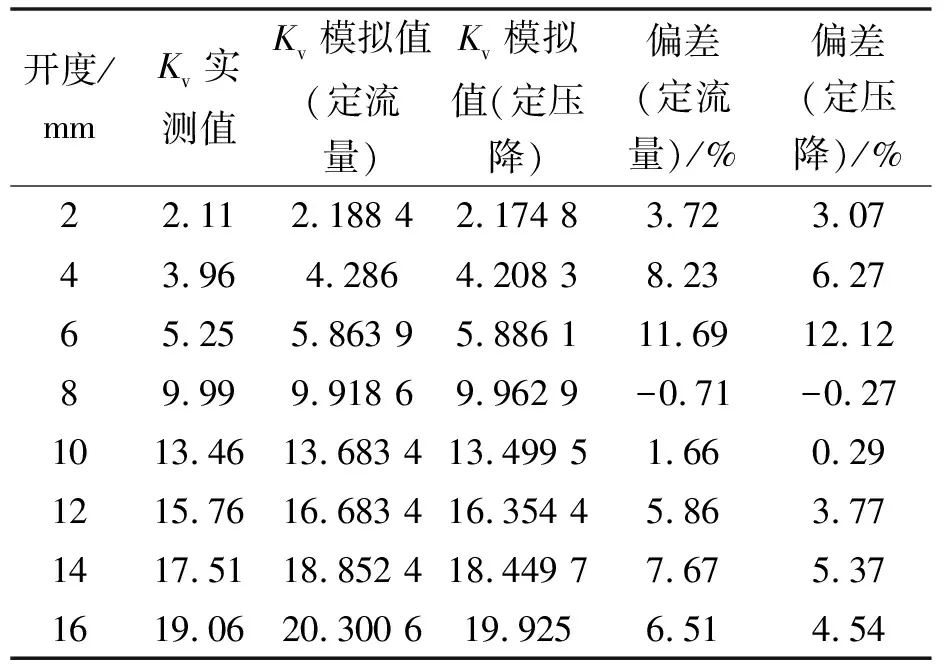
表6 流量系數對比

由表6可知：模擬數據和實測數據高度吻合，忽略模擬中殘差收斂情況以及實際流動中一些不穩定因素所造成的影響，兩者基本一致。在小開度時，模擬值略大，這因為模擬相對理想，而實測數據存在誤差。在實際流動中，同樣流量下的小開度閥門閉合度較高，導致流體容易撞擊到閥門內部各處都會產生壓降，因此閥門流量系數模擬值比實測值略大一些。在大開度時，同樣流量下，實際流動較為平穩，這時更容易受到重力以及渦流等一些不穩定因素的影響，導致實測值要比模擬值略小一些。通過分析得出模擬方案可行，模擬數據可靠，后面將以模擬數據為標桿進行對閥門結構的優化。

3 閥芯優化

3.1 優化方案

設計優化是一種通過充分利用和探索系統中相互作用的協同機制設計復雜系統和子系統的方法[10]。

為了得到具有線性流量系數曲線的柱塞式調節閥閥芯形狀，首先需要利用數值模擬計算原始閥芯各開度下的流量系數，得到各開度下流量系數增量ΔKv，利用數學統計方法，獲取流量系數增量ΔKv樣本分布均值，以計算理論流量系數；比較理論流量系數與實際流量系數的差別，根據流量系數受流通面積影響的思路修改閥芯形狀，計算修改閥芯后的調節閥各開度流量系數，重新獲取樣本均值及樣本標準差，計算理論流量系數增量ΔKv，進而修正閥芯形狀；最終保證線性流量系數曲線在比較均衡的水平下，完成閥芯的設計優化。閥芯的設計流程如圖5所示，在該設計方案中，以流量系數曲線和流量系數增量ΔKv共同作為評價標準。

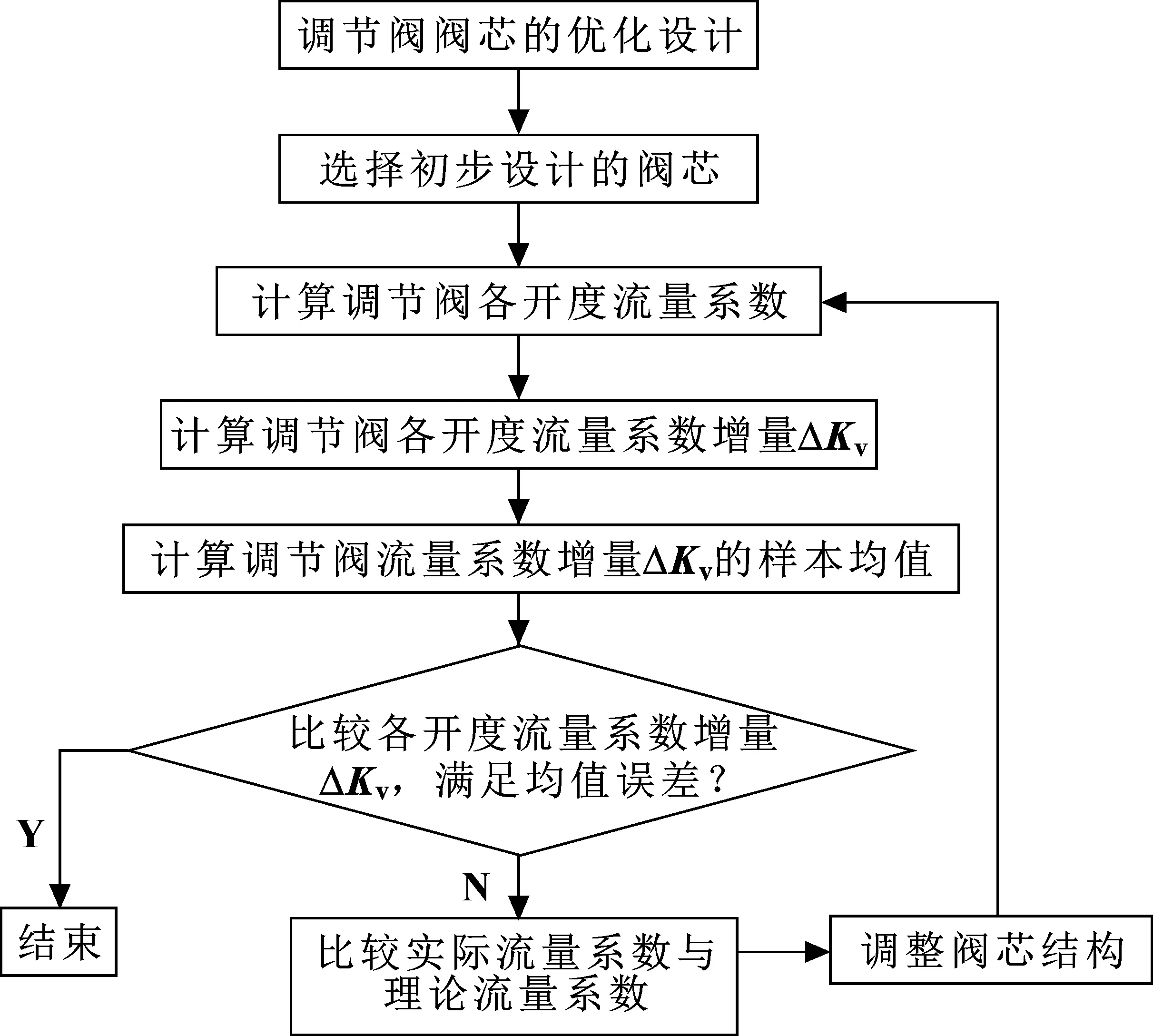
圖5 優化方案流程

3.2 優化步驟與分析

對于此柱塞式調節閥，已知其額定流量系數為20，閥芯行程為16 mm，則可作出該調節閥的理論流量系數曲線以及各開度下的流量系數增量ΔKv均為1.25，將1.25作為流量系數增量的樣本均值，省略了上述方案中反復計算調節閥流量系數增量ΔKv樣本均值的步驟。

為了方便對閥芯結構進行分段優化，在不影響調節閥流量特性的前提下，先將閥芯原有結構形狀沿著BC段進行延伸，閥芯長度由9.9 mm增至12 mm，具體結構變化如圖6所示。

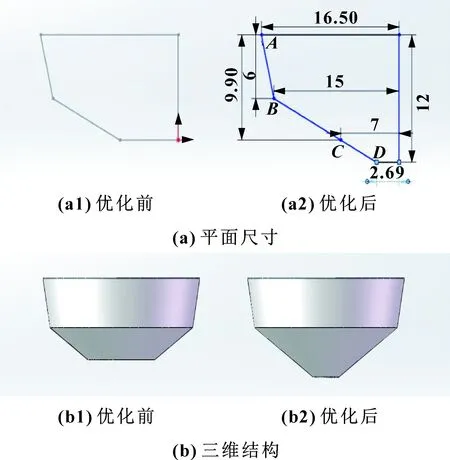
圖6 閥芯延伸示意

通過數值模擬結果發現將閥芯沿著BC段原有的斜率延伸至點D，對調節閥現有流量特性不產生影響。由表7可知：在優化閥芯前，調節閥1-8 mm開度下的流量系數明顯小于理論值，故需要調整閥芯結構使其流通面積變大以使流量系數提高；而在9-16 mm開度下的流量系數明顯大于理論值，故需要調整閥芯結構減小流通面積使其流量系數降低，因此，對閥芯的優化從小開度和大開度逐個出發。

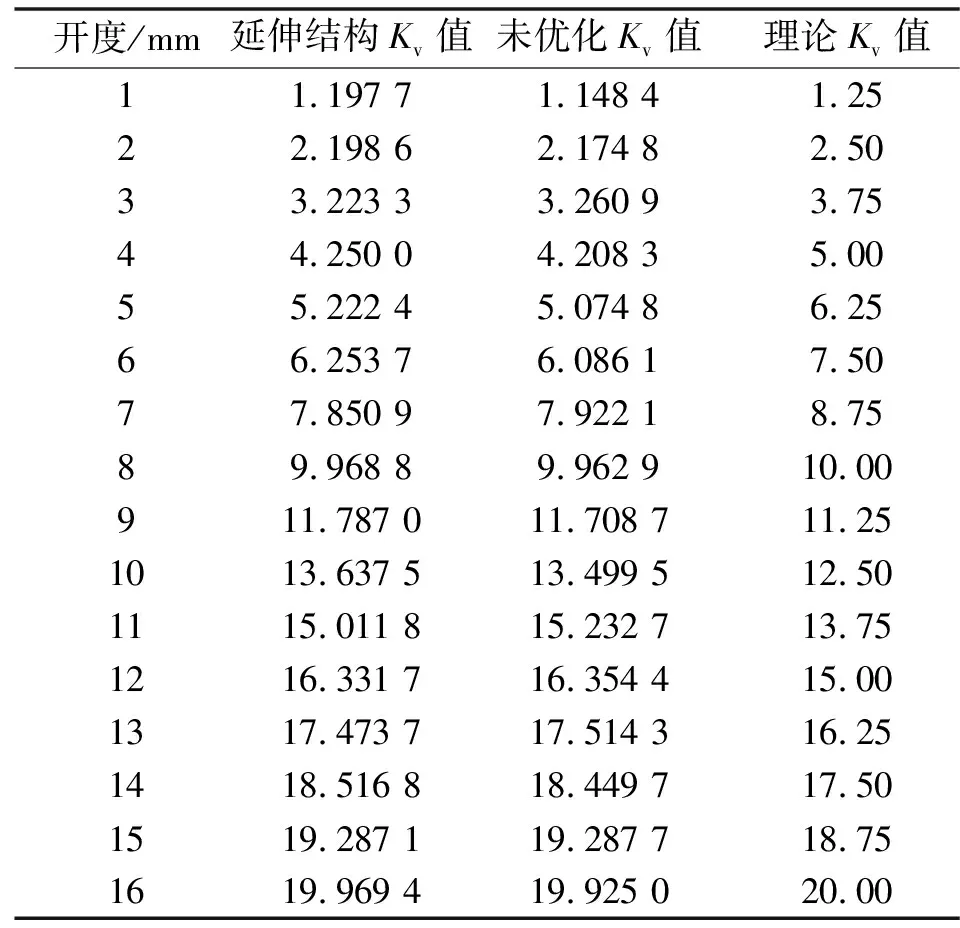
表7 流量系數對比

由于該調節閥為柱塞式，則閥芯的上部分結構即AB段對調節閥小開度流量特性影響較大，閥芯的下半部分結構即BD段對調節閥大開度流量特性影響較大，且小開度下的流量特性基本只受閥芯AB段影響，所以按照以下步驟開始對調節閥的優化。

(1)優化調節閥閥芯AB段結構，在ACD3點確定的前提下，調整點B與閥芯對稱線之間的距離。調整時以0.1 mm為單位，每次調整后對16個開度下的模擬結果進行匯總，發現由優化前的15 mm調整為14.6 mm，可使得調節閥小開度時流量特性較接近線性。具體尺寸變動以及結構變化如圖7所示。

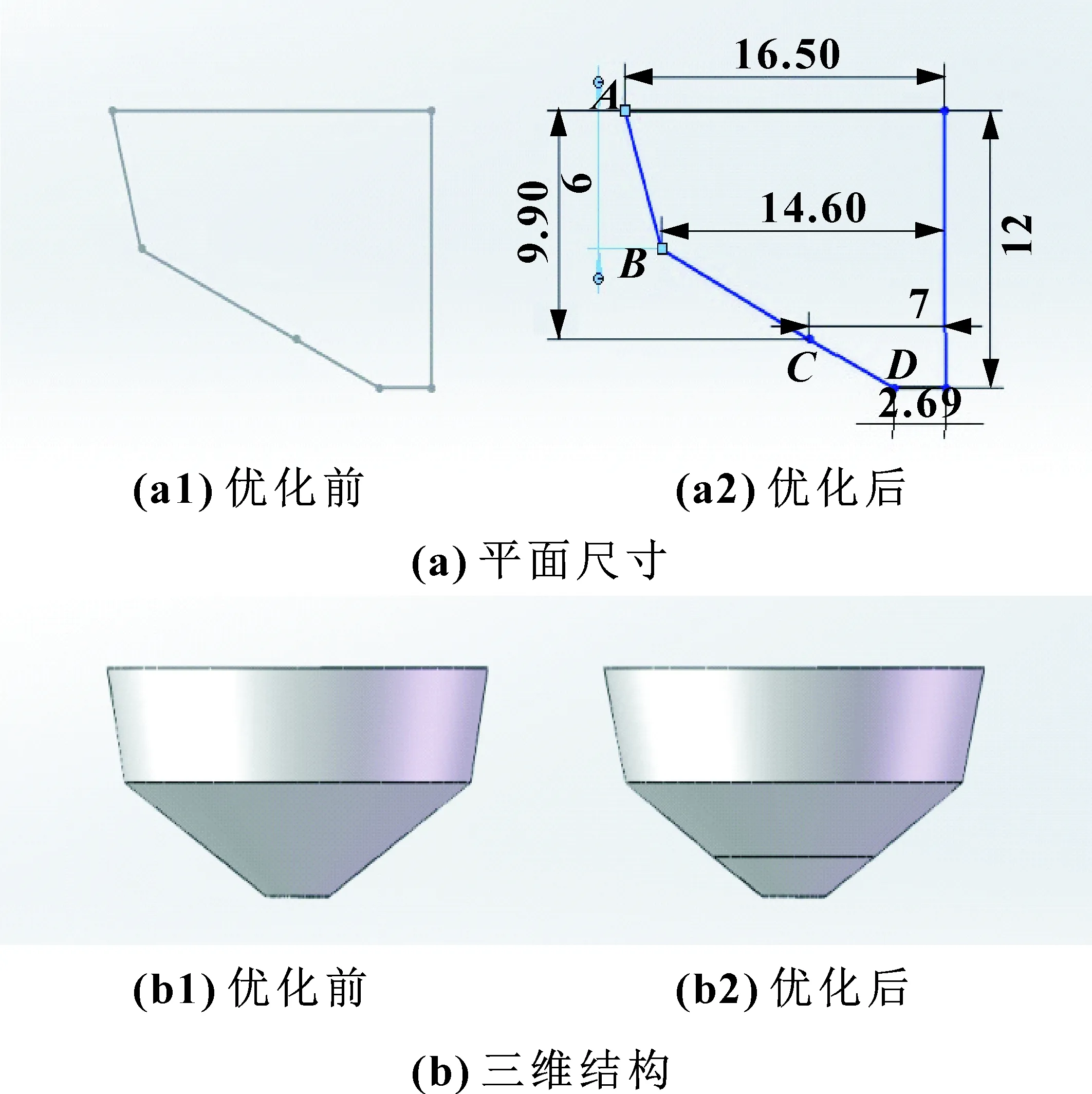
圖7 閥芯第一段結構改動

(2)優化調節閥閥芯BC段結構，在ABD3點確定的前提下，調整點C與閥芯對稱線之間的距離。調整時以0.2 mm為單位，每次調整結構后對16個開度下模擬結果進行匯總，發現由優化前的7 mm調整為12.2 mm，可使得調節閥在9-14 mm的開度區間下流量特性呈線性。具體尺寸變動以及結構變化如圖8所示。

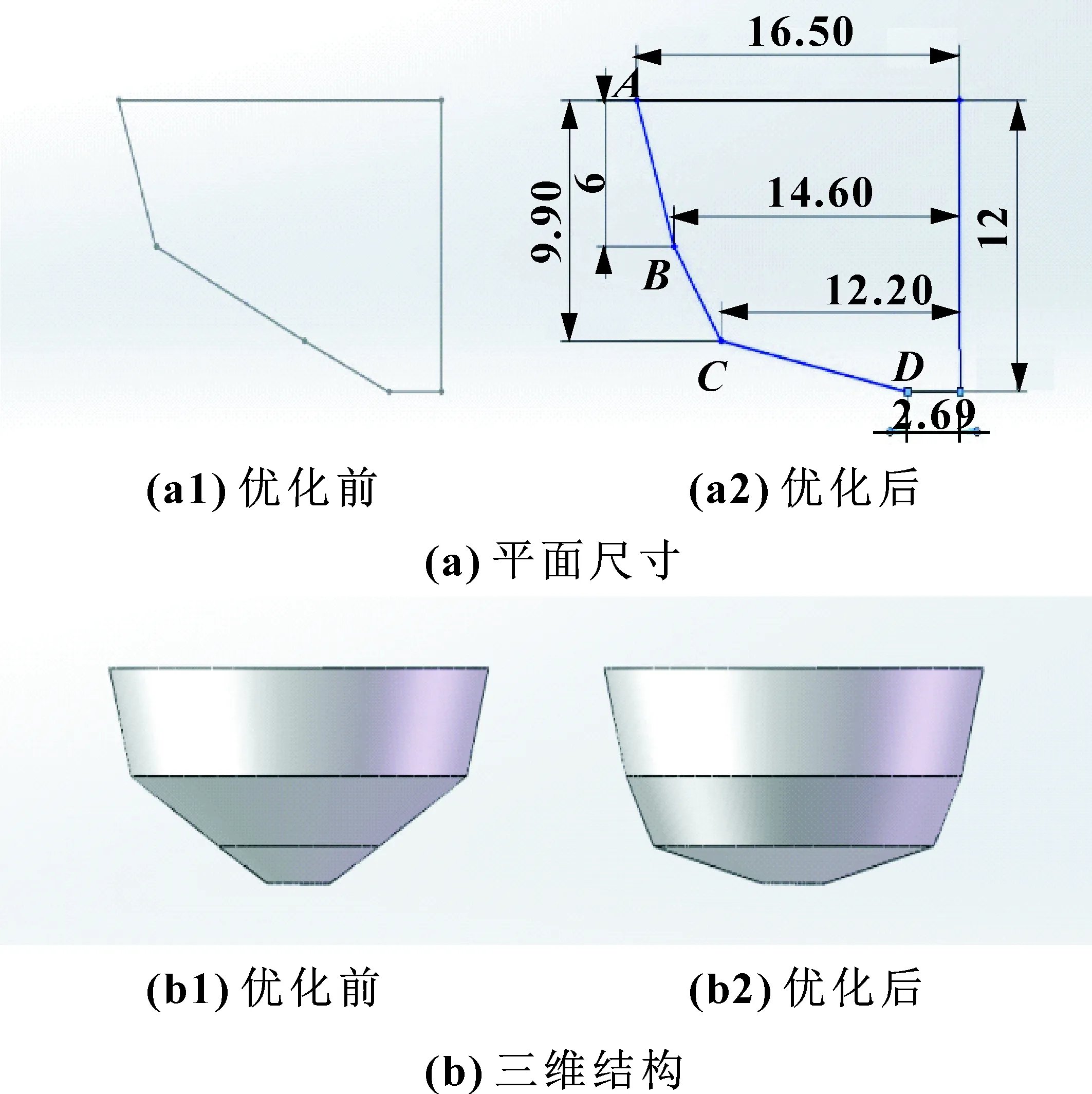
圖8 閥芯第二段結構改動

(3)優化調節閥閥芯CD段結構，由于ABC3點都已經確定，故調整點D與閥芯對稱線之間的距離。調整時以1 mm為單位，每次調整結構后對16個開度下模擬結果進行匯總，發現點D與閥芯對稱線重合時，可使得15、16 mm兩開度下的流量系數更加貼合線性。具體尺寸變動以及結構變化如圖9所示。

圖9 閥芯第三段結構改動

經過以上3次對閥芯結構的分段調整優化，調節閥的流量特征已較貼合直線形，且對它進行仿真模擬時，以1 mm為開度的調節單位，因此，模擬得出的線性流量特征具有較高的可信度。相關數據匯總如表8、9所示。

如表8所示，第一段優化后，1-8 mm開度下的流量系數與理論值已經高度吻合，進一步驗證了1-8 mm開度下的流量系數基本只受閥芯AB段影響；經過第一段、第二段優化后，9-14 mm開度下的流量系數與理論值一致，但由于點C與閥芯對稱線之間的距離從之前的7 mm擴大為12.2 mm，導致調節閥15、16 mm 2個開度下的流量系數變小，此現象表明調節閥的大開度流量特性較容易受到閥芯下半部分結構的影響；則通過第三段優化，將點D向閥芯對稱線靠攏，使得調節閥15、16 mm開度下的流量系數增大并與理論值更加貼合。經過3段優化后的閥芯流量特性高度貼合直線形。

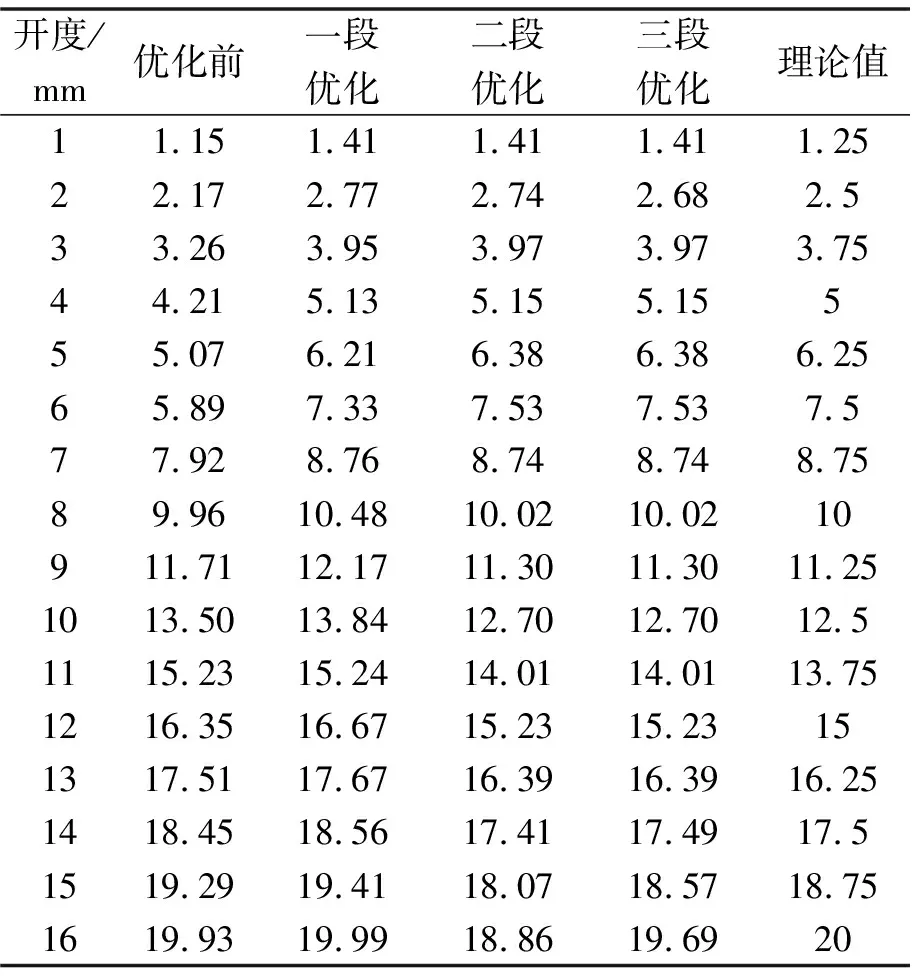
表8 各優化階段流量系數

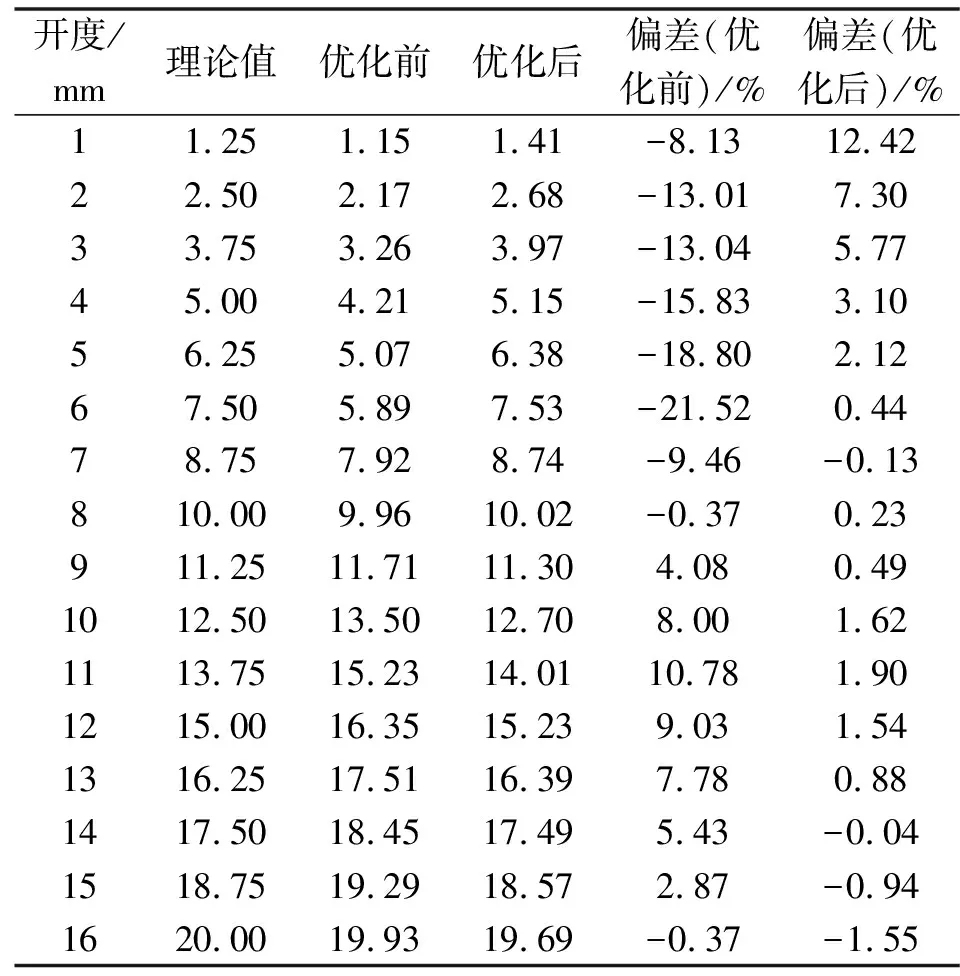
表9 優化前后流量系數偏差

為更好地分析各階段的線性關系，運用數學方法對調節閥各開度流量系數增量進行分析，采用誤差和標準差2種方法，計算誤差和標準差時均以流量系數理論單位增量1.25為樣本均值，相關數據統計如表10、11所示。

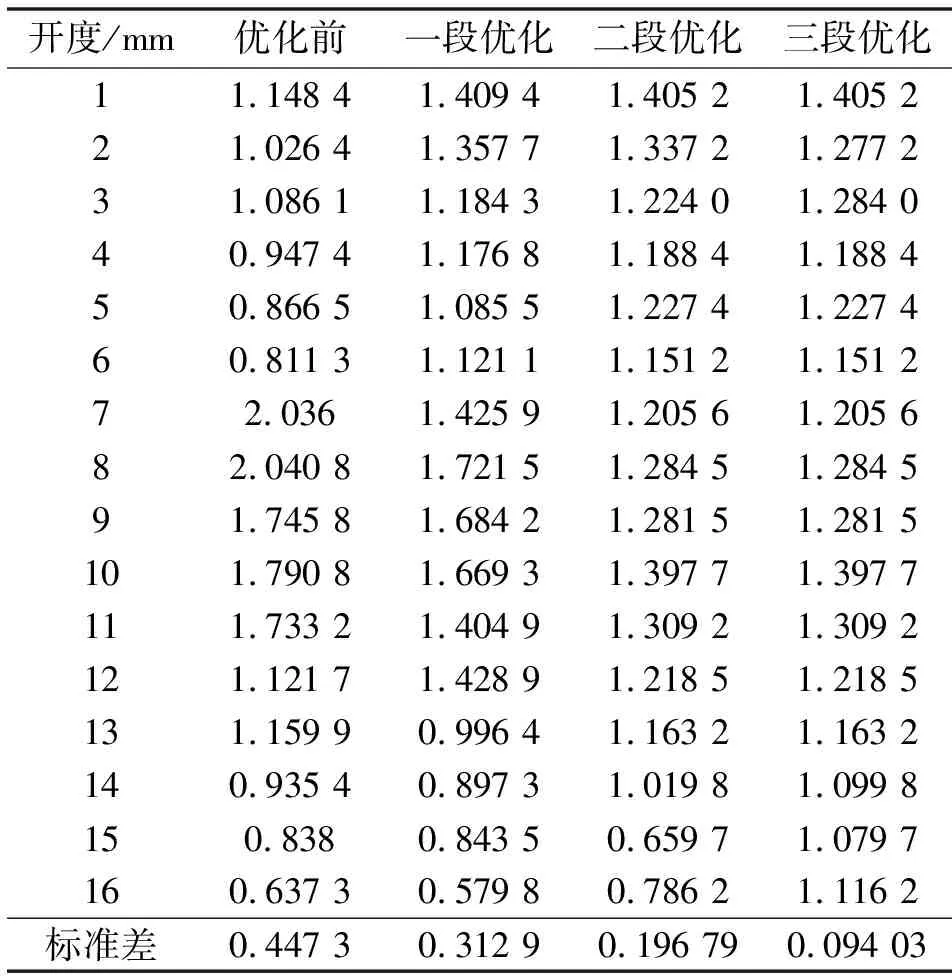
表10 各優化階段流量系數增量

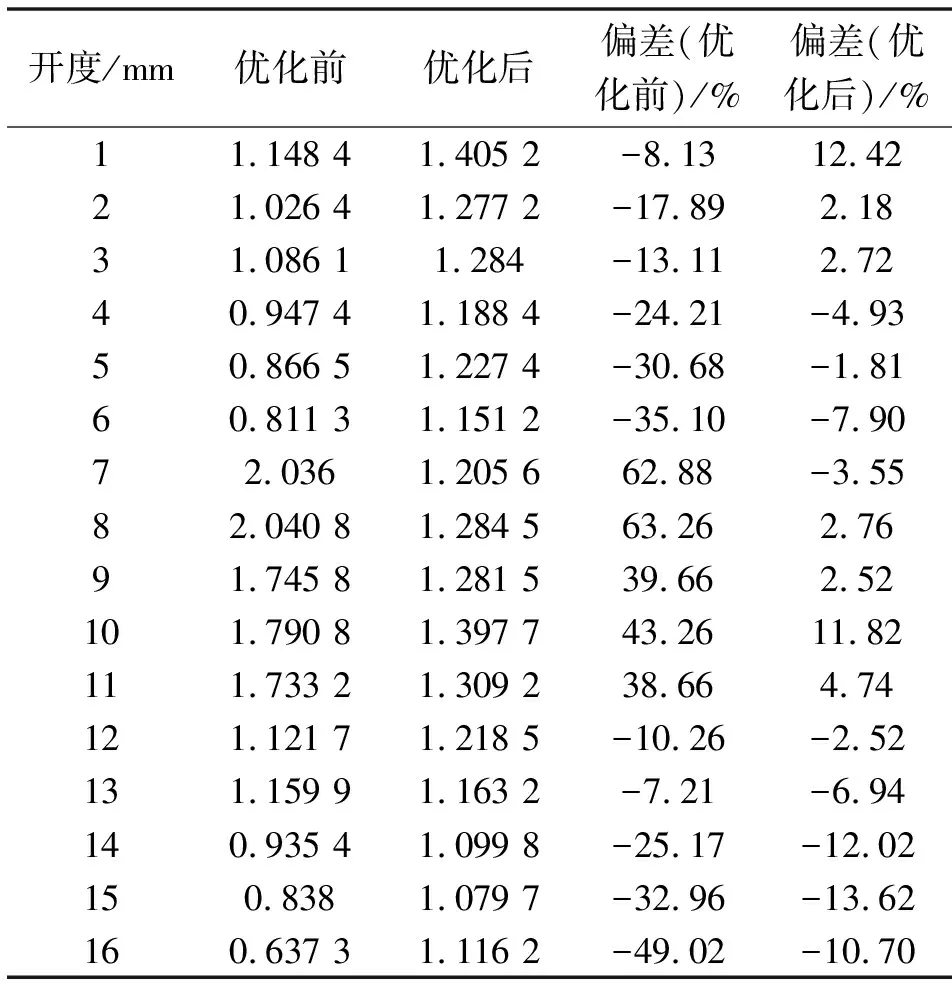
表11 優化前后流量系數增量與理論值偏差對比

標準差作為數理統計中反映個體間離散程度的量，其值越小代表樣本越集中穩定。由表10可以看出，進行3段優化后的流量系數增量的標準差僅為0.094，與未優化結構前的標準差相比少了0.353，故3段優化后的流量系數增量較集中穩定。由表11可以看出：經過3次分段優化后，流量系數增量較理論值最大偏差由未優化前的63.26%降為13.62%，最小偏差由未優化前的7.21%降低為1.81%，均滿足在±15%的偏差內。

4 結論

文中主要闡述一種柱塞式調節閥閥芯的優化設計方案，并通過對DA-J80-40-00型靜態平衡閥的實際優化驗證優化方案的合理性和正確性。針對此優化方案進行的實際工作可得出以下結論：(1)以流量系數和流量系數增量共同作為評判線性貼合度的準則，可以保證優化后的流量特性滿足實際線性需求；(2)對于柱塞式調節閥閥芯結構的優化，采用分段方式可以快速且準確地完成優化；(3)該方案可進一步提升閥門的調節精度，使閥門在管網中運行時更加穩定精確。